help links subscribe changes refresh edit

	FriCAS Algebra
FreeModule ←	↑	→ OrderedVariableList

LinearOperator

last edited 1 year ago by Bill Page

Edit detail for LinearOperator revision 50 of 63

	1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63
Editor: Bill Page Time: 2011/05/10 17:45:22 GMT-7
Note: unevaluated products

changed:
-- it might be useful (but much more complicated) to allow source
-  and target dimensions to be different
\begin{axiom}
)lib CARTEN MONAL PROP
\end{axiom}

changed:
-)abbrev domain LIN LinearOperator
-)lib CARTEN
-LinearOperator(dim:NNI,gen:OrderedFinite,K:CommutativeRing): Exports == Implementation where
)abbrev domain LOP LinearOperator
LinearOperator(gener:OrderedFinite,K:Field): Exports == Implementation where

changed:
-  T ==> CartesianTensor(1,dim,K)
-
-  Exports ==> Join(Ring, BiModule(K,K), Monoidal NNI, RetractableTo K) with
-    inp: List K -> %
-      ++ incoming vector
-    inp: List % -> %
-    out: List K -> %
-      ++ output vector
-    out: List % -> %

  Exports ==> Join(Ring, VectorSpace K, Monoidal NNI, RetractableTo K) with

changed:
-    basisVectors: () -> List %
-    basisForms: () -> List %
-    tensor: % -> T
    basisOut: () -> List %
    basisIn: () -> List %

added:
    eval: % -> %

changed:
-    import NAT
-    Rep == Record(domain:NNI, codomain:NNI, data:T)

    dim:NNI := size()$gener
    T := CartesianTensor(1,dim,K)
    L := Record(domain:NNI, codomain:NNI, data:T)
    RR := Record(gen:L,exp:NNI)
    -- FreeMonoid provides unevaluated products
    Rep == FreeMonoid L

added:
    dimension():CardinalNumber == coerce dim


changed:
-    dom(f:%):NNI == rep(f).domain
-    cod(f:%):NNI == rep(f).codomain
-    dat(f:%):T == rep(f).data
    dom(f:%):NNI ==
      r:NNI := 0
      for y in factors(rep f) repeat
        r:=r+(y.gen.domain)*(y.exp)
      return r
    cod(f:%):NNI ==
      r:NNI := 0
      for y in factors(rep f) repeat
        r:=r+(y.gen.codomain)*(y.exp)
      return r

    prod(f:L,g:L):L ==
      r:T := product(f.data,g.data)
      -- dom(f) + cod(f) + dom(g) + cod(g)
      p:List Integer := concat                _
        [[i for i in 1..(f.domain)],              _
        [(f.domain)+(f.codomain)+i for i in 1..(g.domain)], _
        [(f.domain)+i for i in 1..(f.codomain)],        _
        [(f.domain)+(g.domain)+(f.codomain)+i for i in 1..(g.codomain)]]
        -- dom(f) + dom(g) + cod(f) + cod(g)
      --output("prod p = ",p::OutputForm)$OutputPackage
      [(f.domain)+(g.domain),(f.codomain)+(g.codomain),reindex(r,p)]

    dats(fs:List RR):L ==
      r:L := [0,0,1$T]
      for y in fs repeat
        t:L:=y.gen
        for n in 1..y.exp repeat
          r:=prod(r,t)
      return r

    dat(f:%):L == dats factors rep f
      

added:
    eval(f:%):% == per coerce dat(f)


changed:
-      dom(f)=0 and cod(f)=0 => retract(dat f)$T
      dom(f)=0 and cod(f)=0 => retract(dat(f).data)$T

changed:
-      dom(f)=0 and cod(f)=0 => retract(dat f)$T
      dom(f)=0 and cod(f)=0 => retract(dat(f).data)$T

changed:
-    basisVectors():List % == [per [0,1,entries(row(1,i)$SquareMatrix(dim,K))::T] for i in 1..dim]
-    basisForms():List % == [per [1,0,entries(row(1,i)$SquareMatrix(dim,K))::T] for i in 1..dim]
-    ev(n:NAT):% ==
-      dx:= basisForms()
-      reduce(_+,[ (dx.i)^n * (dx.i)^n for i in 1..dim])
-    co(n:NAT):% == 
-      Dx:= basisVectors()
-      reduce(_+,[ (Dx.i)^n * (Dx.i)^n for i in 1..dim])
    basisOut():List % == [per coerce [0,1,entries(row(1,i)$SquareMatrix(dim,K))::T] for i in 1..dim]
    basisIn():List % == [per coerce [1,0,entries(row(1,i)$SquareMatrix(dim,K))::T] for i in 1..dim]
    ev(n:NAT):% == reduce(_+,[ dx^n * dx^n for dx in basisIn()])$List(%)
    co(n:NAT):% == reduce(_+,[ Dx^n * Dx^n for Dx in basisOut()])$List(%)

changed:
-    map(f:K->K, g:%):% == per [dom g,cod g,unravel(map(f,ravel dat g))$T]
    map(f:K->K, g:%):% == per coerce [dom g,cod g,unravel(map(f,ravel dat(g).data))$T]

changed:
-    ravel(g:%):List K == ravel dat g
    ravel(g:%):List K == ravel dat(g).data

changed:
-      per [dom(p),cod(p),unravel(r)$T]
-    tensor(x:%):T == dat(x)
      per coerce [dom(p),cod(p),unravel(r)$T]

changed:
-      dat(f)=0 => g
-      dat(g)=0 => f
      dat(f).data=0 => g
      dat(g).data=0 => f

changed:
-      per [dom f,cod f,dat(f)+dat(g)]
      per coerce [dom f,cod f,dat(f).data+dat(g).data]

changed:
-      dat(f)=0 => g
-      dat(g)=0 => f
      dat(f).data=0 => g
      dat(g).data=0 => f

changed:
-      per [dom f, cod f,dat(f)-dat(g)]
-
-    _-(f:%):% == per [dom f, cod f,-dat(f)]
-
-    -- repeated sum
-    (p:NNI * f:%):% ==
-      p=1 => f
-      q:=subtractIfCan(p,1)
-      q case NNI => q*f + f
-      -- zero map (non-trivial)
-      per [dom f,cod f,0*dat(f)]
      per coerce [dom f, cod f,dat(f).data-dat(g).data]

    _-(f:%):% == per coerce [dom f, cod f,-dat(f).data]

changed:
-    0 == per [0,0,0]
-    zero?(f:%):Boolean == dat f = 0 * dat f
    0 == per coerce [0,0,0]
    zero?(f:%):Boolean == dat(f).data = 0 * dat(f).data

changed:
-    1:% == per [0,0,1]
-    one?(f:%):Boolean == dat f = 1$T
    1:% == per 1
    one?(f:%):Boolean == one? rep f

changed:
-    I == per([1,1,kroneckerDelta()$T])
-    -- inherited from Ring
-    --(x:% = y:%):Boolean ==
-    --  dom(x) ~= dom(y) or cod(x) ~= cod(y) => error "arity"
-    --  dat(x) = dat(y)
-    (x:% = y:%):Boolean == zero? (x - y)
    I == per coerce [1,1,kroneckerDelta()$T]
    (x:% = y:%):Boolean == rep eval x = rep eval y

changed:
-      per [#p,#p,reindex(dat r,p3)]
-    coerce(p:List None):% == per [0,0,1]
      --output("coerce p3 = ",p3::OutputForm)$OutputPackage
      per coerce [#p,#p,reindex(dat(r).data,p3)]
    coerce(p:List None):% == per coerce [0,0,1]

changed:
-    -- product
    -- tensor product

changed:
-    (f:% * g:%):% ==
-      r:T := product(dat f,dat g)
-      -- dom(f) + cod(f) + dom(g) + cod(g)
-      p:List Integer := concat                _
-        [[i for i in 1..dom(f)],              _
-        [dom(f)+cod(f)+i for i in 1..dom(g)], _
-        [dom(f)+i for i in 1..cod(f)],        _
-        [dom(f)+dom(g)+cod(f)+i for i in 1..cod(g)]]
-        -- dom(f) + dom(g) + cod(f) + cod(g)
-      per [dom(f)+dom(g),cod(f)+cod(g),reindex(r,p)]
-
-    -- repeated product
-    (f:% ^ p:NNI):% ==
-      p=1 => f
-      q:=subtractIfCan(p,1)
-      q case NNI => f^q * f
-      1
    (f:% * g:%):% == per (rep f * rep g)

    leadI(x:Rep):NNI ==
      r:=hclf(x,rep(I)^size(x))
      size(r)=0 => 0
      nthExpon(r,1)

    trailI(x:Rep):NNI ==
      r:=hcrf(x,rep(I)^size(x))
      size(r)=0 => 0
      nthExpon(r,1)

changed:
-      f1:Integer:=dom(f)+1
-      r:T := contract(cod(f),dat f,f1, dat g,1)
-      per [dom(f),cod(g),r]

      -- parallelize composition f/g = (f1/g1)*(f2/g2)
      if cod(f)>0 then
        i:Integer:=1
        j:Integer:=1
        n:NNI:=1
        m:NNI:=1
        f1 := per coerce nthFactor(rep f,1)
        g1 := per coerce nthFactor(rep g,1)
        while cod(f1)~=dom(g1) repeat
          if cod(f1) < dom(g1) then
            if n < nthExpon(rep f,i) then
              n:=n+1
            else
              n:=1
              i:=i+1
            f1 := f1 * per coerce nthFactor(rep f,i)
          else if cod(f1) > dom(g1) then
            if m < nthExpon(rep g,j) then
              m:=m+1
            else
              n:=1
              j:=j+1
            g1 := g1 * per coerce nthFactor(rep g,j)
        f2 := per overlap(rep f1, rep f).rm
        g2 := per overlap(rep g1,rep g).rm
        f := f1
        g := g1
      else
        f2 := per 1
        g2 := per 1

      -- remove leading and trailing identities
      nf := leadI rep f
      f := per overlap(rep(I)^nf,rep f).rm
      ng := leadI rep g
      g := per overlap(rep(I)^ng,rep g).rm
      fn := trailI rep f
      f := per overlap(rep f,rep(I)^fn).lm
      gn := trailI rep g
      g := per overlap(rep g,rep(I)^gn).lm

      -- parallel factors guarantees that these are just identities
      if nf>0 and ng>0 then
        return I*(f2/g2)
      if fn>0 and gn>0 then
        output("Should not happen: trailing [fn,gn] = ",[fn,gn]::OutputForm)$OutputPackage
        return (f/g)*I

      -- Exercise for Reader:
      --   Prove the following contraction and permutation is correct by
      --   considering all 9 cases for (nf=0 or ng=0) and (fn=0 or gn=0).
      -- output("leading [nl,nf,ng] = ",[nl,nf,ng]::OutputForm)$OutputPackage
      -- output("trailing [ln,fn,gn] = ",[ln,fn,gn]::OutputForm)$OutputPackage
      r:T := contract(cod(f)-ng-gn, dat(f).data,dom(f)+ng+1, dat(g).data,nf+1)
      p:List Integer:=concat [ _
        [dom(f)+gn+i for i in 1..nf], _
        [i for i in 1..dom(f)], _
        [dom(f)+nf+ng+i for i in 1..fn], _
        [dom(f)+i for i in 1..ng], _
        [dom(f)+nf+ng+fn+gn+i for i in 1..cod(g)], _
        [dom(f)+ng+i for i in 1..gn] ]
      --print(p::OutputForm)$OutputForm
      r:=reindex(r,p)

      if f2=1 and g2=1 then
        return per coerce [nf+dom(f)+fn,ng+cod(g)+gn,r]
      return per coerce [nf+dom(f)+fn,ng+cod(g)+gn,r] * (f2/g2)

changed:
-      -- optimize leading and trailing identities ?
-      f1:=0; f2:=length(f)-1
-      --for i in 0..length(f)-1 repeat
-      --  if select(f,i)~=I then
-      --    if f1=0 then f1:=i
-      --    f2:=i
-      fs:List % := [select(f,i) for i in f1..f2]
-      g1:=0; g2:=length(g)-1
-      --for i in 0..length(g)-1 repeat
-      --  if select(g,i)~=I then
-      --    if g1=0 then g1:=i
-      --    g2:=i
-      gs:List % := [select(g,i) for i in g1..g2]
      fs:List % := [select(f,i) for i in 0..length(f)-1]
      gs:List % := [select(g,i) for i in 0..length(g)-1]

changed:
-      --f2:=length(f)-1-f2
-      --g2:=length(g)-1-g2
-      --if f1+cod(fr)+f2 ~= g1+dom(gr)+g2 then error "arity"
-      --if cod(fr) < dom(gr) then  -- more inputs
-      --  r:T := contract(cod(fr),dat fr,dom(fr)+1, dat gr,1+f1)
-      --  -- move f1 inputs of gr before inputs of fr and f2 inputs of gr after inputs of fr
-      --  -- r:=reindex(r,[])
-      --  return per [f1+dom(fr)+f2,cod(gr),r]
-      --else  -- more outputs?
-      --  r:T := contract(dom(gr),dat fr,dom(fr)+1+g1, dat gr,1)
-      --  -- move g1 outputs of fr before outputs of gr and g2 outputs of fr after outputs of gr
-      --  -- r:=reindex(r,[])
-      --  return per [dom(fr),g1+cod(gr)+g2,r]
-
-    (x:K * y:%):% == per [dom y, cod y,x*dat(y)]
-    (x:% * y:K):% == per [dom x,cod x,dat(x)*y]
-    (x:Integer * y:%):% == per [dom y,cod y,x*dat(y)]
-
-    -- constructors
-    inp(x:List K):% == per [1,0,entries(x)::T]
-    inp(x:List %):% ==
-      #removeDuplicates([dom(y) for y in x]) ~= 1 or
-        #removeDuplicates([cod(y) for y in x]) ~= 1 => error "arity"
-      per [(dom(first x)+1),cod(first x),[dat(y) for y in x]::T]$Rep
-    out(x:List K):% == per [0,1,entries(x)::T]
-    out(x:List %):% ==
-      #removeDuplicates([dom(y) for y in x])~=1 or
-        #removeDuplicates([cod(y) for y in x])~=1 => error "arity"
-      per [dom(first x),(cod(first x)+1),[dat(y) for y in x]::T]$Rep

    (x:K * y:%):% == per coerce [dom y, cod y,x*dat(y).data]
    (x:% * y:K):% == per coerce [dom x,cod x,dat(x).data*y]
    (x:Integer * y:%):% == per coerce [dom y,cod y,x*dat(y).data]

changed:
-    coerce(x:%):OutputForm ==
-      dom(x)=0 and cod(x)=0 => return dat(x)::OutputForm
-      if size()$gen > 0 then
-        gens:List OutputForm:=[index(i::PositiveInteger)$gen::OutputForm for i in 1..dim]
    show(x:%):OutputForm ==
      dom(x)=0 and cod(x)=0 => return (dat(x).data)::OutputForm
      if size()$gener > 0 then
        gens:List OutputForm:=[index(i::PositiveInteger)$gener::OutputForm for i in 1..dim]

changed:
-        bases:= []
        bases:List OutputForm:= []

changed:
-        for base in bases for k in ravel dat(x) | k~=0]
        for base in bases for k in ravel dat(x).data | k~=0]

added:

    coerce(x:%):OutputForm ==
      r:OutputForm := empty()
      for y in factors(rep x) repeat
        if y.exp = 1 then
          if size rep x = 1 then
            r := show per coerce y.gen
          else
            r:=r*paren(list show per coerce y.gen)
        else
          r:=r*paren(list show per coerce y.gen)^(y.exp::OutputForm)
      return r

changed:
-Conveniences
-
Convenient Notation

changed:
-macro Σ(x,i)==reduce(+,[x for i in 1..dim])
macro Σ(f,i,b) == reduce(+,[f*b.i for i in 1..#b])

changed:
-macro Ξ(f,i)==[f for i in 1..dim]
-\end{axiom}
macro Ξ(f,i)==[f for i in 1..retract(dimension()$L)]
\end{axiom}

changed:
-dim:=2
-Q:=EXPR INT
-L:=LinearOperator(dim,OVAR [x,y],Q)
-Dx:=basisVectors()$L
-dx:=basisForms()$L
-matrix Ξ(Ξ( dx.i * Dx.j, i),j)
Q := EXPR INT
L := LOP(OVAR ['x,'y],Q)
dim:Integer:=retract dimension()$L
Dx:=basisOut()$L
dx:=basisIn()$L
matrix Ξ(Ξ( eval(dx.i * Dx.j), i),j)

changed:
-Ω:=co(1)$L
-U:=ev(1)$L
-Ω / U
-I:L:=[1]
\end{axiom}

Tests
\begin{axiom}
A:L := Σ( Σ( script(a,[[j],[i]]), i,Dx), j,dx)
-- scalar
3*A
A/3
-- identity
I:L := [1]
H:L:=[1,2]
test( I*I = H )
-- twist
X:L := [2,1]
test(X/X=H)
-- printing
I*X*X*I
-- trace
U:L:=ev(1)
Ω:L:=co(1)
Ω/U

added:
Various special cases of composition
\begin{axiom}
-- case 1
test( X/X = [1,2] )
test( (I*X)/(I*X) = [1,2,3] )
test( (I*X*I)/(I*X*I) = [1,2,3,4] )
-- case 2
test( (X*I*I)/(X*X) = [1,2,4,3] )
-- case 3
test( (X*X)/(X*I*I) = [1,2,4,3] )
-- case 4
test ( (I*I*X)/(X*X) = [2,1,3,4] )
-- case 5
test( (I*X*I)/(X*X) = [3,1,4,2] )
-- case 6
test( (I*I*X)/(X*I*I)=[2,1,4,3] )
test( (I*X)/(X*I) = [3,1,2] )
test( (I*X*I)/(X*I*I)=[3,1,2,4] )
-- case 7
test( (X*X)/(I*I*X) = [2,1,3,4] )
-- case 8
test( (X*I)/(I*X) = [2,3,1] )
-- case 9
test( (X*X)/(I*X*I) = [2,4,1,3] )
\end{axiom}


changed:
-A1:L := Σ(superscript(a1,[i])*dx.i,i)
A1:L := Σ(superscript(a1,[i]),i,dx)

changed:
-A2:L := Σ(superscript(a2,[i])*dx.i,i)
-A:L := inp[A1,A2]
A2:L := Σ(superscript(a2,[i]),i,dx)
A:L := A1*I+I*A2

changed:
-B1:L := Σ(subscript(b1,[i])*Dx.i,i)
B1:L := Σ(subscript(b1,[i]),i,Dx)

changed:
-B2:L := Σ(subscript(b2,[i])*Dx.i,i)
-B:L := out[B1,B2]
B2:L := Σ(subscript(b2,[i]),i,Dx)
B:L := B1*I+I*B2

changed:
-BB:L := Σ(Σ(subscript(b,[i,j])*Dx.i*Dx.j,i),j)
-W:L := Σ(Σ(Σ(script(w,[[k],[i,j]])*(Dx.k*dx.i*dx.j),k),i),j)
-\end{axiom}
BB:L := Σ(Σ(subscript(b,[i,j]),i,Dx),j,Dx)
W:L := Σ(Σ(Σ(script(w,[[k],[i,j]]),k,Dx),i,dx),j,dx)
\end{axiom}

removed:
-X2:L:=inp[inp([script(x,[[],[i,j]]) for j in 1..2])$L for i in 1..dim]
-XB21:=X2*B1
-arity(XB21)
-Y2:L:=out[out([script(y,[[i,j]]) for j in 1..2])$L for i in 1..dim]
-XY22:=X2*Y2
-arity(XY22)
-YX22:=Y2*X2
-arity(XY22)

changed:
-Permutations and Identities
-\begin{axiom}
-H:L:=[1,2]
-X:L:=[2,1]
-test(X/X=H)
-\end{axiom}
Permutations
\begin{axiom}
-- braid
B3:=(I*X)/(X*I)
test(B3/B3/B3 = I*I*I)
-- parallel
test((X*X)/(X*X)=H*H)
\end{axiom}

removed:
-tensor AB

changed:
-Y:=Σ(Σ(Σ(script(y,[[k],[i,j]])*Dx.k*dx.i*dx.j,j),i),k)
Y:=Σ(Σ(Σ(script(y,[[k],[i,j]]),j,dx),i,dx),k,Dx)

changed:
-tensor Y
-\end{axiom}
\end{axiom}

changed:
-Algebra
-\begin{axiom}
-Y - [2,1]
-  /   Y
\begin{axiom}
Y -   X /
      Y

changed:
-U:=inp[inp([script(u,[[],[i,j]]) for j in 1..2])$L for i in 1..2]
U:=Σ(Σ(script(u,[[],[i,j]]),j,dx),i,dx)

changed:
-λ:=inp[out[out([script(y,[[i],[j,k]]) for k in 1..2])$L for j in 1..2] for i in 1..2]
λ:=Σ(Σ(Σ(script(y,[[i],[j,k]]),i,dx),j,Dx),k,Dx)

changed:
-tensor λ
-\end{axiom}
\end{axiom}

removed:
-
-From BillPage Thu Mar 10 09:42:33 -0800 2011
-From: Bill Page
-Date: Thu, 10 Mar 2011 09:42:33 -0800
-Subject: Linear operators as morphisms
-Message-ID: <20110310094233-0800@axiom-wiki.newsynthesis.org>
-
-If linear operators really are to be morphisms (in the sense of category theory) then they must have a domain and a co-domain that are vector spaces, not just an in-degree and out-degree.  E.g.::
-
-  Rep == Record(Dom:VectorSpace, Cod:VectorSpace, t:T)
-
-But VectorSpace is a category which would make Dom and Cod domains.  The domains that currently satisfy VectorSpace in Axiom are rather limited and seem oddly focused on number theory (finite fields). It is a good thing however that DirectProduct is a conditional member of this cateogry.
-\begin{axiom}
-DirectProduct(2,FRAC INT) has VectorSpace(FRAC INT)
-\end{axiom}
-Unfortunately:
-\begin{axiom}
-DirectProduct(2,DirectProduct(2,FRAC INT)) has VectorSpace(FRAC INT)
-\end{axiom}
-
-The problem with VectorSpace is that the domain [Vector] is not a member of this category instead it satisfies VectoryCategory.
-
-Is it possible to treat tensors from CartesianTensor as maps from VectorSpace to VectorSpace? We would like for example::
-
-  T:DirectProduct(dim,DirectProduct(dim,FRAC INT)) -> DirectProduct(dim,FRAC INT))
-
-To be a linear operator with two inputs and one output.
-
-From BillPage Thu Mar 10 16:03:13 -0800 2011
-From: Bill Page
-Date: Thu, 10 Mar 2011 16:03:13 -0800
-Subject: Modules
-Message-ID: <20110310160313-0800@axiom-wiki.newsynthesis.org>
-
-A [FreeModule] over a [Field] is a VectorSpace unfortunately this is not currently understood by Axiom:
-\begin{axiom}
-FreeModule(Fraction Integer,OrderedVariableList [e1,e1]) has VectorSpace(Fraction Integer)
-\end{axiom}
-
-From BillPage Thu Apr 28 12:31:32 -0700 2011
-From: Bill Page
-Date: Thu, 28 Apr 2011 12:31:32 -0700
-Subject: 
-Message-ID: <20110428123132-0700@axiom-wiki.newsynthesis.org>
-
-SandBoxLinearOperator - experiments with lazy evaluation of products
-
-From BillPage Mon May 9 16:38:25 -0700 2011
-From: Bill Page
-Date: Mon, 09 May 2011 16:38:25 -0700
-Subject: Two-color compact closed category
-Message-ID: <20110509163825-0700@axiom-wiki.newsynthesis.org>
-
-SandBoxCompactClosedLinearOperator
-
-Ref: http://en.wikipedia.org/wiki/Compact_closed_category

Introduction

Bi-graded linear operators (transformations) over n-dimensional vector spaces on a commutative ring 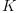. Members of this domain are morphisms 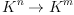$K^n \to K^m$ . Products, permutations and composition (grafting) of morphisms are implemented. Operators are represented internally as tensors.

Operator composition and products can be visualized by directed graphs (read from top to bottom) such as:

      n = 3     inputs
      m = 0     outputs

$\scalebox{1} % Change this value to rescale the drawing. { \begin{pspicture}(0,-0.92)(4.82,0.92) \psbezier[linewidth=0.04](2.2,0.9)(2.2,0.1)(2.6,0.1)(2.6,0.9) \psline[linewidth=0.04cm](2.4,0.3)(2.4,-0.1) \psbezier[linewidth=0.04](2.4,-0.1)(2.4,-0.9)(3.0,-0.9)(3.0,-0.1) \psline[linewidth=0.04cm](3.0,-0.1)(3.0,0.9) \psbezier[linewidth=0.04](4.8,0.9)(4.8,0.1)(4.4,0.1)(4.4,0.9) \psline[linewidth=0.04cm](4.6,0.3)(4.6,-0.1) \psbezier[linewidth=0.04](4.6,-0.1)(4.6,-0.9)(4.0,-0.9)(4.0,-0.1) \psline[linewidth=0.04cm](4.0,-0.1)(4.0,0.9) \usefont{T1}{ptm}{m}{n} \rput(3.4948437,0.205){=} \psline[linewidth=0.04cm](0.6,-0.7)(0.6,0.9) \psbezier[linewidth=0.04](0.0,-0.1)(0.0,-0.9)(1.2,-0.9)(1.2,-0.1) \psline[linewidth=0.04cm](0.0,-0.1)(0.0,0.9) \psline[linewidth=0.04cm](1.2,-0.1)(1.2,0.9) \usefont{T1}{ptm}{m}{n} \rput(1.6948438,0.205){=} \end{pspicture} }$

External vertices in this graph represent vectors, and tensors. Internal nodes and arcs (edges) represent linear operators. Horizontal juxtaposition (i.e. a horizontal cross-section) represents tensor product. Vertical juxtaposition represents operator composition.

See examples and documentation below

I would like you to make brief comments in the form at the bottom of this web page. For more detailed but related comments click discussion on the top menu.

Regards, Bill Page.

Source Code

We try to start the right way by defining the concept of a monoidal category.

Ref: http://en.wikipedia.org/wiki/PROP_(category_theory)

spad

)abbrev category MONAL Monoidal
Monoidal(R:AbelianSemiGroup):Category == Ring with
    dom: % -> R
      ++ domain
    cod: % -> R
      ++ co-domain
    _/: (%,%) -> %
      ++ vertical composition f/g
    apply:(%,%) -> %
      ++ horizontal product f g = f*g

spad

   Compiling FriCAS source code from file 
      /var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/2074022068168685528-25px001.spad
      using old system compiler.
   MONAL abbreviates category Monoidal 
------------------------------------------------------------------------
   initializing NRLIB MONAL for Monoidal 
   compiling into NRLIB MONAL 

;;;     ***       |Monoidal| REDEFINED
Time: 0 SEC.

   finalizing NRLIB MONAL 
   Processing Monoidal for Browser database:
--->-->Monoidal(constructor): Not documented!!!!
--------(dom (R %))---------
--------(cod (R %))---------
--------(/ (% % %))---------
--->-->Monoidal((/ (% % %))): Improper first word in comments: vertical
"vertical composition \\spad{f/g}"
--------(apply (% % %))---------
--->-->Monoidal((apply (% % %))): Improper first word in comments: horizontal
"horizontal product \\spad{f} \\spad{g} = \\spad{f*g}"
--->-->Monoidal(): Missing Description
; compiling file "/var/aw/var/LatexWiki/MONAL.NRLIB/MONAL.lsp" (written 01 APR 2013 07:31:38 PM):

; /var/aw/var/LatexWiki/MONAL.NRLIB/MONAL.fasl written
; compilation finished in 0:00:00.005
------------------------------------------------------------------------
   Monoidal is now explicitly exposed in frame initial 
   Monoidal will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/MONAL.NRLIB/MONAL

The initial object in this category is the domain Prop (Products and Permutations). The Prop domain represents everything that is "constant" about all the domains in this category. It can be defined as an endo-functor with only the information available about the category itself.

spad

)abbrev domain PROP Prop
Prop(L:Monoidal NNI): Exports == Implementation where
  NNI ==> NonNegativeInteger

  Exports ==> Monoidal NNI with
    coerce: L -> %

  Implementation ==> add
    Rep == Record(domain:NNI, codomain:NNI)                -- Rep == L
    rep(x:%):Rep == x pretend Rep
    per(x:Rep):% == x pretend %

    coerce(f:%):OutputForm == dom(f)::OutputForm / cod(f)::OutputForm

    coerce(f:L):% == per [dom f, cod f]                    -- coerce(f:L):% == per f

    dom(x:%):NNI == rep(x).domain                          -- dom(x:%):NNI == dom rep x
    cod(x:%):NNI == rep(x).codomain                        -- cod(x:%):NNI == cod rep x
    0:% == per [0,0]                                       -- 0:% == per 0
    1:% == per [0,0]                                       -- 1:% == per 1
    -- evaluation
    (f:% / g:%):% == per [dom f, cod g]                    -- (f:% / g:%):% == per (rep f / rep g)
    -- product
    apply(f:%,g:%):% == per [dom f + dom g, cod f + cod g] -- apply(f:%,g:%):% == per apply(rep f,rep g)
    (f:% * g:%):% == per [dom f + dom g, cod f + cod g]    --(f:% * g:%):% == per (rep f * rep g)
    -- sum
    (f:% + g:%):% == per [dom f, cod f]                    --(f:% + g:%):% == per (rep f + rep g)

spad

   Compiling FriCAS source code from file 
      /var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/3714416860228184972-25px002.spad
      using old system compiler.
   PROP abbreviates domain Prop 
------------------------------------------------------------------------
   initializing NRLIB PROP for Prop 
   compiling into NRLIB PROP 
************* USER ERROR **********
available signatures for Rep: 
    NONE
NEED Rep: () -> ?
****** comp fails at level 1 with expression: ******
((DEF (|Rep|) (NIL) (NIL)
  (|Record| (|:| |domain| (|NonNegativeInteger|))
            (|:| |codomain| (|NonNegativeInteger|)))))
****** level 1  ******
$x:= (DEF (Rep) (NIL) (NIL) (Record (: domain (NonNegativeInteger)) (: codomain (NonNegativeInteger))))
$m:= $EmptyMode
$f:=
((((|$Information| #) (~= #) (= #) (|coerce| #) ...)))

   >> Apparent user error:
   unspecified error

The LinearOperator? domain is Moniodal over NonNegativeInteger?. The objects of this domain are all tensor powers of a vector space of fixed dimension. The arrows are linear operators that map from one object (tensor power) to another.

Ref: http://en.wikipedia.org/wiki/Category_of_vector_spaces

all members of this domain have the same dimension

axiom

)lib CARTEN MONAL PROP

   CartesianTensor is now explicitly exposed in frame initial 
   CartesianTensor will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/CARTEN.NRLIB/CARTEN
   Monoidal is already explicitly exposed in frame initial 
   Monoidal will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/MONAL.NRLIB/MONAL
   Prop is now explicitly exposed in frame initial 
   Prop will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/PROP.NRLIB/PROP

spad

)abbrev domain LOP LinearOperator
LinearOperator(gener:OrderedFinite,K:Field): Exports == Implementation where
  NNI ==> NonNegativeInteger
  NAT ==> PositiveInteger

  Exports ==> Join(Ring, VectorSpace K, Monoidal NNI, RetractableTo K) with
    arity: % -> Prop %
    basisOut: () -> List %
    basisIn: () -> List %
    map: (K->K,%) -> %
    if K has Evalable(K) then Evalable(K)
    eval: % -> %
    ravel: % -> List K
    unravel: (Prop %,List K) -> %
    coerce:(x:List NAT) -> %
      ++ identity for composition and permutations of its products
    coerce:(x:List None) -> %
      ++ [] = 1
    elt: (%,%) -> %
    elt: (%,NAT) -> %
    elt: (%,NAT,NAT) -> %
    elt: (%,NAT,NAT,NAT) -> %
    _/: (Tuple %,Tuple %) -> %
    _/: (Tuple %,%) -> %
    _/: (%,Tuple %) -> %
      ++ yet another syntax for product
    ev: NAT -> %
      ++ (2,0)-tensor for evaluation
    co: NAT -> %
      ++ (0,2)-tensor for co-evaluation

  Implementation ==> add
    import List NNI

    dim:NNI := size()$gener
    T := CartesianTensor(1,dim,K)
    L := Record(domain:NNI, codomain:NNI, data:T)
    RR := Record(gen:L,exp:NNI)
    -- FreeMonoid provides unevaluated products
    Rep == FreeMonoid L
    rep(x:%):Rep == x pretend Rep
    per(x:Rep):% == x pretend %

    dimension():CardinalNumber == coerce dim

    -- Prop (arity)
    dom(f:%):NNI ==
      r:NNI := 0
      for y in factors(rep f) repeat
        r:=r+(y.gen.domain)*(y.exp)
      return r
    cod(f:%):NNI ==
      r:NNI := 0
      for y in factors(rep f) repeat
        r:=r+(y.gen.codomain)*(y.exp)
      return r

    prod(f:L,g:L):L ==
      r:T := product(f.data,g.data)
      -- dom(f) + cod(f) + dom(g) + cod(g)
      p:List Integer := concat                _
        [[i for i in 1..(f.domain)],              _
        [(f.domain)+(f.codomain)+i for i in 1..(g.domain)], _
        [(f.domain)+i for i in 1..(f.codomain)],        _
        [(f.domain)+(g.domain)+(f.codomain)+i for i in 1..(g.codomain)]]
        -- dom(f) + dom(g) + cod(f) + cod(g)
      --output("prod p = ",p::OutputForm)$OutputPackage
      [(f.domain)+(g.domain),(f.codomain)+(g.codomain),reindex(r,p)]

    dats(fs:List RR):L ==
      r:L := [0,0,1$T]
      for y in fs repeat
        t:L:=y.gen
        for n in 1..y.exp repeat
          r:=prod(r,t)
      return r

    dat(f:%):L == dats factors rep f

    arity(f:%):Prop % == f::Prop %

    eval(f:%):% == per coerce dat(f)

    retractIfCan(f:%):Union(K,"failed") ==
      dom(f)=0 and cod(f)=0 => retract(dat(f).data)$T
      return "failed"
    retract(f:%):K ==
      dom(f)=0 and cod(f)=0 => retract(dat(f).data)$T
      error "failed"

    -- basis
    basisOut():List % == [per coerce [0,1,entries(row(1,i)$SquareMatrix(dim,K))::T] for i in 1..dim]
    basisIn():List % == [per coerce [1,0,entries(row(1,i)$SquareMatrix(dim,K))::T] for i in 1..dim]
    ev(n:NAT):% == reduce(_+,[ dx^n * dx^n for dx in basisIn()])$List(%)
    co(n:NAT):% == reduce(_+,[ Dx^n * Dx^n for Dx in basisOut()])$List(%)

    -- manipulation
    map(f:K->K, g:%):% == per coerce [dom g,cod g,unravel(map(f,ravel dat(g).data))$T]
    if K has Evalable(K) then
      eval(g:%,f:List Equation K):% == map((x:K):K+->eval(x,f),g)
    ravel(g:%):List K == ravel dat(g).data
    unravel(p:Prop %,r:List K):% ==
      dim^(dom(p)+cod(p)) ~= #r => error "failed"
      per coerce [dom(p),cod(p),unravel(r)$T]

    -- sum
    (f:% + g:%):% ==
      dat(f).data=0 => g
      dat(g).data=0 => f
      dom(f) ~= dom(g) or cod(f) ~= cod(g) => error "arity"
      per coerce [dom f,cod f,dat(f).data+dat(g).data]

    (f:% - g:%):% ==
      dat(f).data=0 => g
      dat(g).data=0 => f
      dom(f) ~= dom(f) or cod(g) ~= cod(g) => error "arity"
      per coerce [dom f, cod f,dat(f).data-dat(g).data]

    _-(f:%):% == per coerce [dom f, cod f,-dat(f).data]

    -- identity for sum (trivial zero map)
    0 == per coerce [0,0,0]
    zero?(f:%):Boolean == dat(f).data = 0 * dat(f).data
    -- identity for product
    1:% == per 1
    one?(f:%):Boolean == one? rep f
    -- identity for composition
    I == per coerce [1,1,kroneckerDelta()$T]
    (x:% = y:%):Boolean == rep eval x = rep eval y

    -- permutations and identities
    coerce(p:List NAT):% ==
      r:=I^#p
      #p = 1 and p.1 = 1 => return r
      p1:List Integer:=[i for i in 1..#p]
      p2:List Integer:=[#p+i for i in p]
      p3:=concat(p1,p2)
      --output("coerce p3 = ",p3::OutputForm)$OutputPackage
      per coerce [#p,#p,reindex(dat(r).data,p3)]
    coerce(p:List None):% == per coerce [0,0,1]
    coerce(x:K):% == 1*x

    -- tensor product
    elt(f:%,g:%):% == f * g
    elt(f:%,g:NAT):% == f * I^g
    elt(f:%,g1:NAT,g2:NAT):% == f * [g1 @ NAT,g2 @ NAT]::List NAT::%
    elt(f:%,g1:NAT,g2:NAT,g3:NAT):% == f * [g1 @ NAT,g2 @ NAT,g3 @ NAT]::List NAT::%
    apply(f:%,g:%):% == f * g
    (f:% * g:%):% == per (rep f * rep g)

    leadI(x:Rep):NNI ==
      r:=hclf(x,rep(I)^size(x))
      size(r)=0 => 0
      nthExpon(r,1)

    trailI(x:Rep):NNI ==
      r:=hcrf(x,rep(I)^size(x))
      size(r)=0 => 0
      nthExpon(r,1)

    -- composition:
    -- f/g : A^n -> A^p = f:A^n -> A^m / g:A^m -> A^p
    (ff:% / gg:%):% ==
      g:=gg; f:=ff
      -- partial application from the left
      n:=subtractIfCan(cod ff,dom gg)
      if n case NNI and n>0 then
      -- apply g on f from the left, pass extra f outputs on the right
        print(hconcat([message("arity warning: "), _
              over(arity(ff)::OutputForm, _
                   arity(gg)::OutputForm*(arity(I)::OutputForm)^n::OutputForm) ]))$OutputForm
        g:=gg*I^n
      m:=subtractIfCan(dom gg, cod ff)
      --  apply g on f from the left, add extra g inputs on the left
      if m case NNI and m>0 then
        print(hconcat([message("arity warning: "), _
              over((arity(I)::OutputForm)^m::OutputForm*arity(ff)::OutputForm, _
                   arity(gg)::OutputForm)]))$OutputForm
        f:=I^m*ff

      -- parallelize composition f/g = (f1/g1)*(f2/g2)
      if cod(f)>0 then
        i:Integer:=1
        j:Integer:=1
        n:NNI:=1
        m:NNI:=1
        f1 := per coerce nthFactor(rep f,1)
        g1 := per coerce nthFactor(rep g,1)
        while cod(f1)~=dom(g1) repeat
          if cod(f1) < dom(g1) then
            if n < nthExpon(rep f,i) then
              n:=n+1
            else
              n:=1
              i:=i+1
            f1 := f1 * per coerce nthFactor(rep f,i)
          else if cod(f1) > dom(g1) then
            if m < nthExpon(rep g,j) then
              m:=m+1
            else
              n:=1
              j:=j+1
            g1 := g1 * per coerce nthFactor(rep g,j)
        f2 := per overlap(rep f1, rep f).rm
        g2 := per overlap(rep g1,rep g).rm
        f := f1
        g := g1
      else
        f2 := per 1
        g2 := per 1

      -- remove leading and trailing identities
      nf := leadI rep f
      f := per overlap(rep(I)^nf,rep f).rm
      ng := leadI rep g
      g := per overlap(rep(I)^ng,rep g).rm
      fn := trailI rep f
      f := per overlap(rep f,rep(I)^fn).lm
      gn := trailI rep g
      g := per overlap(rep g,rep(I)^gn).lm

      -- parallel factors guarantees that these are just identities
      if nf>0 and ng>0 then
        return I*(f2/g2)
      if fn>0 and gn>0 then
        output("Should not happen: trailing [fn,gn] = ",[fn,gn]::OutputForm)$OutputPackage
        return (f/g)*I

      -- Exercise for Reader:
      --   Prove the following contraction and permutation is correct by
      --   considering all 9 cases for (nf=0 or ng=0) and (fn=0 or gn=0).
      -- output("leading [nl,nf,ng] = ",[nl,nf,ng]::OutputForm)$OutputPackage
      -- output("trailing [ln,fn,gn] = ",[ln,fn,gn]::OutputForm)$OutputPackage
      r:T := contract(cod(f)-ng-gn, dat(f).data,dom(f)+ng+1, dat(g).data,nf+1)
      p:List Integer:=concat [ _
        [dom(f)+gn+i for i in 1..nf], _
        [i for i in 1..dom(f)], _
        [dom(f)+nf+ng+i for i in 1..fn], _
        [dom(f)+i for i in 1..ng], _
        [dom(f)+nf+ng+fn+gn+i for i in 1..cod(g)], _
        [dom(f)+ng+i for i in 1..gn] ]
      --print(p::OutputForm)$OutputForm
      r:=reindex(r,p)

      if f2=1 and g2=1 then
        return per coerce [nf+dom(f)+fn,ng+cod(g)+gn,r]
      return per coerce [nf+dom(f)+fn,ng+cod(g)+gn,r] * (f2/g2)

    -- another notation for composition of products
    (t:Tuple % / x:%):% == t / construct([x])$PrimitiveArray(%)::Tuple(%)
    (x:% / t:Tuple %):% == construct([x])$PrimitiveArray(%)::Tuple(%) / t
    (f:Tuple % / g:Tuple %):% ==
      fs:List % := [select(f,i) for i in 0..length(f)-1]
      gs:List % := [select(g,i) for i in 0..length(g)-1]
      fr:=reduce(elt@(%,%)->%,fs,1)
      gr:=reduce(elt@(%,%)->%,gs,1)
      fr / gr

    (x:K * y:%):% == per coerce [dom y, cod y,x*dat(y).data]
    (x:% * y:K):% == per coerce [dom x,cod x,dat(x).data*y]
    (x:Integer * y:%):% == per coerce [dom y,cod y,x*dat(y).data]

    -- display operators using basis
    show(x:%):OutputForm ==
      dom(x)=0 and cod(x)=0 => return (dat(x).data)::OutputForm
      if size()$gener > 0 then
        gens:List OutputForm:=[index(i::PositiveInteger)$gener::OutputForm for i in 1..dim]
      else
        -- default to numeric indices
        gens:List OutputForm:=[i::OutputForm for i in 1..dim]
      -- input basis
      inps:List OutputForm := []
      for i in 1..dom(x) repeat
        empty? inps => inps:=gens
        inps:=concat [[(inps.k * gens.j) for j in 1..dim] for k in 1..#inps]
      -- output basis
      outs:List OutputForm := []
      for i in 1..cod(x) repeat
        empty? outs => outs:=gens
        outs:=concat [[(outs.k * gens.j) for j in 1..dim] for k in 1..#outs]
      -- combine input (superscripts) and/or output(subscripts) to form basis symbols
      bases:List OutputForm
      if #inps > 0 and #outs > 0 then
        bases:=concat([[ scripts(message("|"),[i,j]) for i in outs] for j in inps])
      else if #inps > 0 then
        bases:=[super(message("|"),i) for i in inps]
      else if #outs > 0 then
        bases:=[sub(message("|"),j) for j in outs]
      else
        bases:List OutputForm:= []
      -- merge bases with data to form term list
      terms:=[(k=1 => base;k::OutputForm*base)
        for base in bases for k in ravel dat(x).data | k~=0]
      empty? terms => return 0::OutputForm
      -- combine the terms
      return reduce(_+,terms)

    coerce(x:%):OutputForm ==
      r:OutputForm := empty()
      for y in factors(rep x) repeat
        if y.exp = 1 then
          if size rep x = 1 then
            r := show per coerce y.gen
          else
            r:=r*paren(list show per coerce y.gen)
        else
          r:=r*paren(list show per coerce y.gen)^(y.exp::OutputForm)
      return r

spad

   Compiling FriCAS source code from file 
      /var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/3050628105245683310-25px004.spad
      using old system compiler.
   LOP abbreviates domain LinearOperator 
------------------------------------------------------------------------
   initializing NRLIB LOP for LinearOperator 
   compiling into NRLIB LOP 
   importing List NonNegativeInteger
************* USER ERROR **********
available signatures for Rep: 
    NONE
NEED Rep: () -> ?
****** comp fails at level 1 with expression: ******
((DEF (|Rep|) (NIL) (NIL) (|FreeMonoid| L)))
****** level 1  ******
$x:= (DEF (Rep) (NIL) (NIL) (FreeMonoid L))
$m:= $EmptyMode
$f:=
((((|copy| #) (|setelt| #) (|exp| #) (|setelt| #) ...)))

   >> Apparent user error:
   unspecified error

Getting Started

Consult the source code above for more details.

Convenient Notation

axiom

-- summation
macro Σ(f,i,b) == reduce(+,[f*b.i for i in 1..#b])

Type: Void

axiom

-- list comprehension
macro Ξ(f,i)==[f for i in 1..retract(dimension()$L)]

Type: Void

Basis

axiom

Q := EXPR INT

$\label{eq1}\hbox{\axiomType{Expression}\ } (\hbox{\axiomType{Integer}\ })$

(1)

Type: Type

axiom

L := LOP(OVAR ['x,'y],Q)

   LinearOperator is an unknown constructor and so is unavailable. Did 
      you mean to use -> but type something different instead?
dim:Integer:=retract dimension()$L

   The function dimension is not implemented in NIL .
Dx:=basisOut()$L

   The function basisOut is not implemented in NIL .
dx:=basisIn()$L

   The function basisIn is not implemented in NIL .
matrix Ξ(Ξ( eval(dx.i * Dx.j), i),j)

   The function dimension is not implemented in NIL .
matrix Ξ(Ξ( Dx.i / dx.j, i),j)

   The function dimension is not implemented in NIL .

Tests

axiom

A:L := Σ( Σ( script(a,[[j],[i]]), i,Dx), j,dx)

   There are 2 exposed and 1 unexposed library operations named # 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op #
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named # 
      with argument type(s) 
                                Variable(dx)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
-- scalar
3*A

$\label{eq2}3 \ A$

(2)

Type: Polynomial(Integer)

axiom

A/3

$\label{eq3}{1 \over 3}\ A$

(3)

Type: Polynomial(Fraction(Integer))

axiom

-- identity
I:L := [1]

$\label{eq4}\left[ 1 \right]$

(4)

Type: List(PositiveInteger?)

axiom

H:L:=[1,2]

$\label{eq5}\left[ 1, \: 2 \right]$

(5)

Type: List(PositiveInteger?)

axiom

test( I*I = H )

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
-- twist
X:L := [2,1]

$\label{eq6}\left[ 2, \: 1 \right]$

(6)

Type: List(PositiveInteger?)

axiom

test(X/X=H)

   There are 13 exposed and 12 unexposed library operations named / 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op /
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named / 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
-- printing
I*X*X*I

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
-- trace
U:L:=ev(1)

   There are no library operations named ev 
      Use HyperDoc Browse or issue
                                 )what op ev
      to learn if there is any operation containing " ev " in its name.

   Cannot find a definition or applicable library operation named ev 
      with argument type(s) 
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
Ω:L:=co(1)

   There are no library operations named co 
      Use HyperDoc Browse or issue
                                 )what op co
      to learn if there is any operation containing " co " in its name.

   Cannot find a definition or applicable library operation named co 
      with argument type(s) 
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
Ω/U

$\label{eq7}�� \over U$

(7)

Type: Fraction(Polynomial(Integer))

axiom

test
  ( I Ω  ) /
  (  U I ) = I

   There are no exposed library operations named I but there is one 
      unexposed operation with that name. Use HyperDoc Browse or issue
                                )display op I
      to learn more about the available operation.

   Cannot find a definition or applicable library operation named I 
      with argument type(s) 
                                 Variable(Ω)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
test
  (  Ω I ) /
  ( I U  ) = I

   There are no library operations named Ω 
      Use HyperDoc Browse or issue
                                 )what op Ω
      to learn if there is any operation containing " Ω " in its name.

   Cannot find a definition or applicable library operation named Ω 
      with argument type(s) 
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Various special cases of composition

axiom

-- case 1
test( X/X = [1,2] )

   There are 13 exposed and 12 unexposed library operations named / 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op /
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named / 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
test( (I*X)/(I*X) = [1,2,3] )

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
test( (I*X*I)/(I*X*I) = [1,2,3,4] )

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
-- case 2
test( (X*I*I)/(X*X) = [1,2,4,3] )

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
-- case 3
test( (X*X)/(X*I*I) = [1,2,4,3] )

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
-- case 4
test ( (I*I*X)/(X*X) = [2,1,3,4] )

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
-- case 5
test( (I*X*I)/(X*X) = [3,1,4,2] )

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
-- case 6
test( (I*I*X)/(X*I*I)=[2,1,4,3] )

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
test( (I*X)/(X*I) = [3,1,2] )

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
test( (I*X*I)/(X*I*I)=[3,1,2,4] )

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
-- case 7
test( (X*X)/(I*I*X) = [2,1,3,4] )

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
-- case 8
test( (X*I)/(I*X) = [2,3,1] )

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
-- case 9
test( (X*X)/(I*X*I) = [2,4,1,3] )

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Construction

axiom

A1:L := Σ(superscript(a1,[i]),i,dx)

   There are 2 exposed and 1 unexposed library operations named # 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op #
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named # 
      with argument type(s) 
                                Variable(dx)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
arity A1

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                                Variable(A1)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
A2:L := Σ(superscript(a2,[i]),i,dx)

   There are 2 exposed and 1 unexposed library operations named # 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op #
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named # 
      with argument type(s) 
                                Variable(dx)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
A:L := A1*I+I*A2

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                                Variable(A1)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
arity A

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                                 Variable(A)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
B1:L := Σ(subscript(b1,[i]),i,Dx)

   There are 2 exposed and 1 unexposed library operations named # 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op #
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named # 
      with argument type(s) 
                                Variable(Dx)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
arity B1

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                                Variable(B1)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
B2:L := Σ(subscript(b2,[i]),i,Dx)

   There are 2 exposed and 1 unexposed library operations named # 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op #
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named # 
      with argument type(s) 
                                Variable(Dx)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
B:L := B1*I+I*B2

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                                Variable(B1)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
arity B

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                                 Variable(B)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
BB:L := Σ(Σ(subscript(b,[i,j]),i,Dx),j,Dx)

   There are 2 exposed and 1 unexposed library operations named # 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op #
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named # 
      with argument type(s) 
                                Variable(Dx)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
W:L := Σ(Σ(Σ(script(w,[[k],[i,j]]),k,Dx),i,dx),j,dx)

   There are 2 exposed and 1 unexposed library operations named # 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op #
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named # 
      with argument type(s) 
                                Variable(dx)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Composition (evaluation)

$g/f : A^n \to A^{m+p} = f:A^n \to A^m <em> g:A^n \to A^p$

axiom

AB2 := A2 / B2; AB2::OutputForm = A2::OutputForm / B2::OutputForm

$\label{eq8}{A 2 \over B 2}={A 2 \over B 2}$

(8)

Type: Equation(OutputForm?)

axiom

arity(AB2)::OutputForm = arity(A2)::OutputForm / arity(B2)::OutputForm

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                        Fraction(Polynomial(Integer))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
BA1 := B1 / A1; BA1::OutputForm = B1::OutputForm / A1::OutputForm

$\label{eq9}{B 1 \over A 1}={B 1 \over A 1}$

(9)

Type: Equation(OutputForm?)

axiom

arity(BA1)::OutputForm = arity(B1)::OutputForm / arity(A1)::OutputForm

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                        Fraction(Polynomial(Integer))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
AB1 := A1 / B1; AB1::OutputForm = A1::OutputForm / B1::OutputForm

$\label{eq10}{A 1 \over B 1}={A 1 \over B 1}$

(10)

Type: Equation(OutputForm?)

axiom

arity(AB1)::OutputForm = arity(A1)::OutputForm / arity(B1)::OutputForm

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                        Fraction(Polynomial(Integer))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Partial Evaluation

axiom

BBA1 := B/A1

$\label{eq11}B \over A 1$

(11)

Type: Fraction(Polynomial(Integer))

axiom

BBA2 := B/B1

$\label{eq12}B \over B 1$

(12)

Type: Fraction(Polynomial(Integer))

axiom

BBA3 := A1/A

$\label{eq13}A 1 \over A$

(13)

Type: Fraction(Polynomial(Integer))

axiom

BBA4 := B1/A

$\label{eq14}B 1 \over A$

(14)

Type: Fraction(Polynomial(Integer))

Powers

axiom

AB3:=(AB1*AB1)*AB1;

Type: Fraction(Polynomial(Integer))

axiom

arity(AB3)

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                        Fraction(Polynomial(Integer))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
test(AB3=AB1*(AB1*AB1))

$\label{eq15} \mbox{\rm true}$

(15)

Type: Boolean

axiom

test(AB3=AB1^3)

$\label{eq16} \mbox{\rm true}$

(16)

Type: Boolean

axiom

one? (AB3^0)

$\label{eq17} \mbox{\rm true}$

(17)

Type: Boolean

Sums

$f+g : A^n \to A^m = f:A^n \to A^m + g:A^n \to A^m$

axiom

A12s := A1 + A2; A12s::OutputForm = A1::OutputForm + A2::OutputForm

$\label{eq18}{A 2 + A 1}={A 1 + A 2}$

(18)

Type: Equation(OutputForm?)

axiom

arity(A12s)::OutputForm = arity(A1)::OutputForm + arity(A2)::OutputForm

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                             Polynomial(Integer)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
B12s := B1 + B2; B12s::OutputForm = B1::OutputForm + B2::OutputForm

$\label{eq19}{B 2 + B 1}={B 1 + B 2}$

(19)

Type: Equation(OutputForm?)

axiom

arity(B12s)::OutputForm = arity(B1)::OutputForm + arity(B2)::OutputForm

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                             Polynomial(Integer)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
-B12s

$\label{eq20}- B 2 - B 1$

(20)

Type: Polynomial(Integer)

axiom

zero? (A12s - A12s)

$\label{eq21} \mbox{\rm true}$

(21)

Type: Boolean

Multiplication

axiom

A3s:=(A1+A1)+A1

$\label{eq22}3 \ A 1$

(22)

Type: Polynomial(Integer)

axiom

arity(A3s)

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                             Polynomial(Integer)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
test(A3s=A1+(A1+A1))

$\label{eq23} \mbox{\rm true}$

(23)

Type: Boolean

axiom

test(A3s=A1*3)

$\label{eq24} \mbox{\rm true}$

(24)

Type: Boolean

axiom

zero? (0*A3s)

$\label{eq25} \mbox{\rm true}$

(25)

Type: Boolean

axiom

B3s:=(B1+B1)+B1

$\label{eq26}3 \ B 1$

(26)

Type: Polynomial(Integer)

axiom

arity(B3s)

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                             Polynomial(Integer)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
test(B3s=B1+(B1+B1))

$\label{eq27} \mbox{\rm true}$

(27)

Type: Boolean

axiom

test(B3s=B1*3)

$\label{eq28} \mbox{\rm true}$

(28)

Type: Boolean

Product

axiom

AB11:=A1*B1

$\label{eq29}A 1 \ B 1$

(29)

Type: Polynomial(Integer)

axiom

arity(AB11)

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                             Polynomial(Integer)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
BA11:= B1*A1

$\label{eq30}A 1 \ B 1$

(30)

Type: Polynomial(Integer)

axiom

arity(BA11)

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                             Polynomial(Integer)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
AB := A*B

$\label{eq31}A \ B$

(31)

Type: Polynomial(Integer)

axiom

arity(AB)

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                             Polynomial(Integer)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
BA := B*A

$\label{eq32}A \ B$

(32)

Type: Polynomial(Integer)

axiom

arity(BA)

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                             Polynomial(Integer)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
WB1:=W*B1

$\label{eq33}B 1 \ W$

(33)

Type: Polynomial(Integer)

axiom

arity(WB1)

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                             Polynomial(Integer)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
test((A*A)*A=A*(A*A))

$\label{eq34} \mbox{\rm true}$

(34)

Type: Boolean

axiom

test((B*B)*B=B*(B*B))

$\label{eq35} \mbox{\rm true}$

(35)

Type: Boolean

axiom

test((A*B)*A=A*(B*A))

$\label{eq36} \mbox{\rm true}$

(36)

Type: Boolean

Permutations

axiom

-- braid
B3:=(I*X)/(X*I)

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
test(B3/B3/B3 = I*I*I)

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
-- parallel
test((X*X)/(X*X)=H*H)

   There are 35 exposed and 33 unexposed library operations named * 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named * 
      with argument type(s) 
                            List(PositiveInteger)
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Manipulations

axiom

ravel AB

   There are 1 exposed and 0 unexposed library operations named ravel 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op ravel
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named ravel
      with argument type(s) 
                             Polynomial(Integer)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
test(unravel(arity AB,ravel AB)$L=AB)

   The function unravel is not implemented in NIL .
map(x+->x+1,AB)$L

   The function map is not implemented in NIL .
[superscript(a1,[i])=i for i in 1..dim]::List EQ Q

   dim is declared as being in Integer but has not been given a value.
eval(A,[superscript(a1,[i])=i for i in 1..dim]::List EQ Q)

   dim is declared as being in Integer but has not been given a value.

Examples

Another kind of diagram:


     Y  =  Y 
    U       U

Algebra

axiom

Y:=Σ(Σ(Σ(script(y,[[k],[i,j]]),j,dx),i,dx),k,Dx)

   There are 2 exposed and 1 unexposed library operations named # 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op #
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named # 
      with argument type(s) 
                                Variable(Dx)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
arity Y

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                                 Variable(Y)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Commutator

axiom

Y -   X /
      Y

   There are 13 exposed and 12 unexposed library operations named / 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op /
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named / 
      with argument type(s) 
                            List(PositiveInteger)
                                 Variable(Y)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Pairing

axiom

U:=Σ(Σ(script(u,[[],[i,j]]),j,dx),i,dx)

   There are 2 exposed and 1 unexposed library operations named # 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op #
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named # 
      with argument type(s) 
                                Variable(dx)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
arity U

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                                 Variable(U)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

3-point function

axiom

YU := Y I
  /    U

   There are no exposed library operations named Y but there are 2 
      unexposed operations with that name. Use HyperDoc Browse or issue
                                )display op Y
      to learn more about the available operations.

   Cannot find a definition or applicable library operation named Y 
      with argument type(s) 
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
YU := Y.I
  /    U

   There are no exposed library operations named Y but there are 2 
      unexposed operations with that name. Use HyperDoc Browse or issue
                                )display op Y
      to learn more about the available operations.

   Cannot find a definition or applicable library operation named Y 
      with argument type(s) 
                            List(PositiveInteger)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
arity YU

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                                Variable(YU)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

axiom

YU:L := (Y,I) / U

   There are 13 exposed and 12 unexposed library operations named / 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op /
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named / 
      with argument type(s) 
                                 Tuple(Any)
                                 Variable(U)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
UY:L := (I,Y) / U

   There are 13 exposed and 12 unexposed library operations named / 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op /
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named / 
      with argument type(s) 
                                 Tuple(Any)
                                 Variable(U)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Oddities (should work on the right)

axiom

YU := Y [1]
  /    U

$\label{eq37}{Y_{1}}\over U$

(37)

Type: Fraction(Polynomial(Integer))

axiom

YU := Y.[1]
  /    U

$\label{eq38}{Y_{1}}\over U$

(38)

Type: Fraction(Polynomial(Integer))

Ok on the left

axiom

UY := [1].Y
  /      U

   There are 1 exposed and 1 unexposed library operations named elt 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                               )display op elt
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find application of object of type List(NonNegativeInteger) 
      to argument(s) of type(s) 
                                 Variable(Y)

UY := [1] Y
  /      U

   There are 1 exposed and 1 unexposed library operations named elt 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                               )display op elt
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find application of object of type List(NonNegativeInteger) 
      to argument(s) of type(s) 
                                 Variable(Y)

arity UY

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                                Variable(UY)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Co-algebra

axiom

λ:=Σ(Σ(Σ(script(y,[[i],[j,k]]),i,dx),j,Dx),k,Dx)

   There are 2 exposed and 1 unexposed library operations named # 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op #
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named # 
      with argument type(s) 
                                Variable(Dx)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
arity λ

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                                 Variable(λ)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Handle

λ
Y

axiom

Φ := λ
  /  Y

$\label{eq39}�� \over Y$

(39)

Type: Fraction(Polynomial(Integer))

axiom

arity Φ

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
                        Fraction(Polynomial(Integer))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Edit detail for LinearOperator revision 50 of 63

Introduction

Source Code

Getting Started

Examples

Comments