Edit detail for LinearOperator revision 12 of 63

Linear transformations (operators) over n-dimensional cartesian vector spaces over a commutative ring 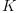. Members of this domain are morphisms 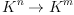. Products, co-products and composition (grafting) of morphisms is implemented. Operators are represented internally as tensors.

Operator composition and products can be visualized by directed graphs (read from top to bottom) such as:

      n = 3     inputs

      \  |  /         \  /   /         \              |
       \ | /           \/   /           \            / \
        \|/             \  /           / \          /   \
        / \              \/           /   \         \   /
       /   \              \          /   / \         \ /
      /     \              \        /   /   \         |

      m = 2     outputs

Lines (edges) in the graph represent vectors, nodes represent operators. Horizontal juxtaposition represents product. Vertical juxtaposition represents composition.

We try to start the right way by defining the concept of a monoidal category.

)abbrev category MONAL Monoidal
Monoidal(R:AbelianSemiGroup):Category == BasicType with
    dom: % -> R
      ++ domain
    cod: % -> R
      ++ co-domain
    _*: (%,%) -> %
      ++ composition
    _/: (%,%) -> %
      ++ vertical composition f/g = g*f
    elt:(%,%) -> %
      ++ horizontal composition (product)
  add
    (f:% / g:%):% == g*f

   Compiling FriCAS source code from file 
      /var/zope2/var/LatexWiki/1467253716425331323-25px001.spad using 
      old system compiler.
   MONAL abbreviates category Monoidal 
------------------------------------------------------------------------
   initializing NRLIB MONAL for Monoidal 
   compiling into NRLIB MONAL 

;;;     ***       |Monoidal| REDEFINED
Time: 0.06 SEC.

   MONAL- abbreviates domain Monoidal& 
------------------------------------------------------------------------
   initializing NRLIB MONAL- for Monoidal& 
   compiling into NRLIB MONAL- 
   compiling exported / : (S,S) -> S
Time: 0.32 SEC.

(time taken in buildFunctor:  0)

;;;     ***       |Monoidal&| REDEFINED
Time: 0.01 SEC.

   Cumulative Statistics for Constructor Monoidal&
      Time: 0.33 seconds

   finalizing NRLIB MONAL- 
   Processing Monoidal& for Browser database:
--------(dom (R %))---------
--------(cod (R %))---------
--------(* (% % %))---------
--------(/ (% % %))---------
--->-->Monoidal&((/ (% % %))): Improper first word in comments: vertical
"vertical composition \\spad{f/g} = \\spad{g*f}"
--------(elt (% % %))---------
--->-->Monoidal&((elt (% % %))): Improper first word in comments: horizontal
"horizontal composition (\\spad{product})"
--->-->Monoidal&(constructor): Not documented!!!!
--->-->Monoidal&(): Missing Description
; compiling file "/var/zope2/var/LatexWiki/MONAL-.NRLIB/MONAL-.lsp" (written 09 APR 2011 07:57:49 AM):

; /var/zope2/var/LatexWiki/MONAL-.NRLIB/MONAL-.fasl written
; compilation finished in 0:00:00.071
------------------------------------------------------------------------
   Monoidal& is now explicitly exposed in frame initial 
   Monoidal& will be automatically loaded when needed from 
      /var/zope2/var/LatexWiki/MONAL-.NRLIB/MONAL-
   finalizing NRLIB MONAL 
   Processing Monoidal for Browser database:
--------(dom (R %))---------
--------(cod (R %))---------
--------(* (% % %))---------
--------(/ (% % %))---------
--->-->Monoidal((/ (% % %))): Improper first word in comments: vertical
"vertical composition \\spad{f/g} = \\spad{g*f}"
--------(elt (% % %))---------
--->-->Monoidal((elt (% % %))): Improper first word in comments: horizontal
"horizontal composition (\\spad{product})"
--->-->Monoidal(constructor): Not documented!!!!
--->-->Monoidal(): Missing Description
; compiling file "/var/zope2/var/LatexWiki/MONAL.NRLIB/MONAL.lsp" (written 09 APR 2011 07:57:49 AM):

; /var/zope2/var/LatexWiki/MONAL.NRLIB/MONAL.fasl written
; compilation finished in 0:00:00.018
------------------------------------------------------------------------
   Monoidal is now explicitly exposed in frame initial 
   Monoidal will be automatically loaded when needed from 
      /var/zope2/var/LatexWiki/MONAL.NRLIB/MONAL

   >> System error:
   The bounding indices 163 and 162 are bad for a sequence of length 162.
See also:
  The ANSI Standard, Glossary entry for "bounding index designator"
  The ANSI Standard, writeup for Issue SUBSEQ-OUT-OF-BOUNDS:IS-AN-ERROR

The initial object in this category is the domain Prop (Products and Permutations).

)abbrev domain PROP Prop
Prop(R:AbelianSemiGroup): Join(Monoidal R, CoercibleTo OutputForm) with
    _/:(R,R) -> %
  == add
    Rep == Record(domain:R,codomain:R)
    rep(x:%):Rep == x pretend Rep
    per(x:Rep):% == x pretend %

    dom(f:%):R == rep(f).domain
    cod(f:%):R == rep(f).codomain

    coerce(f:%):OutputForm == dom(f)::OutputForm / cod(f)::OutputForm
    (f:R / g:R):% == per [f,g]
    (g:% * f:%):% ==
      cod(f) ~= dom(g) => error "arity"
      per [dom f,cod g]
    elt(f:%,g:%):% == per [dom(f)+dom(g),cod(f)+cod(g)]

   Compiling FriCAS source code from file 
      /var/zope2/var/LatexWiki/3672717930539873036-25px002.spad using 
      old system compiler.
   PROP abbreviates domain Prop 
------------------------------------------------------------------------
   initializing NRLIB PROP for Prop 
   compiling into NRLIB PROP 
   compiling local rep : $ -> Record(domain: R,codomain: R)
      PROP;rep is replaced by x 
Time: 0.02 SEC.

   compiling local per : Record(domain: R,codomain: R) -> $
      PROP;per is replaced by x 
Time: 0 SEC.

   compiling exported dom : $ -> R
Time: 0 SEC.

   compiling exported cod : $ -> R
Time: 0 SEC.

   compiling exported coerce : $ -> OutputForm
Time: 0 SEC.

   compiling exported / : (R,R) -> $
Time: 0 SEC.

   compiling exported * : ($,$) -> $
Time: 0 SEC.

   compiling exported elt : ($,$) -> $
Time: 0 SEC.

(time taken in buildFunctor:  0)

;;;     ***       |Prop| REDEFINED

;;;     ***       |Prop| REDEFINED
Time: 0.01 SEC.

   Cumulative Statistics for Constructor Prop
      Time: 0.03 seconds

   finalizing NRLIB PROP 
   Processing Prop for Browser database:
--->-->Prop((/ (% R R))): Not documented!!!!
--->-->Prop(constructor): Not documented!!!!
--->-->Prop(): Missing Description
; compiling file "/var/zope2/var/LatexWiki/PROP.NRLIB/PROP.lsp" (written 09 APR 2011 07:57:50 AM):

; /var/zope2/var/LatexWiki/PROP.NRLIB/PROP.fasl written
; compilation finished in 0:00:00.086
------------------------------------------------------------------------
   Prop is now explicitly exposed in frame initial 
   Prop will be automatically loaded when needed from 
      /var/zope2/var/LatexWiki/PROP.NRLIB/PROP

   >> System error:
   The bounding indices 163 and 162 are bad for a sequence of length 162.
See also:
  The ANSI Standard, Glossary entry for "bounding index designator"
  The ANSI Standard, writeup for Issue SUBSEQ-OUT-OF-BOUNDS:IS-AN-ERROR

The LinearOperator? domain is Moniodal over NonNegativeInteger?

)abbrev domain LIN LinearOperator
LinearOperator(dim:NonNegativeInteger,K:CommutativeRing): Exports == Implementation where
  NNI ==> NonNegativeInteger

  Exports ==> Join(Ring, BiModule(K,K), Monoidal NNI, CoercibleTo Prop NNI) with
    inp: List K -> %
      ++ incoming vector
    inp: List % -> %
    out: List K -> %
      ++ output vector
    out: List % -> %
    coerce: SquareMatrix(dim,K) -> %
    _*: (%,NonNegativeInteger) -> %

  Implementation ==> add
    import List NNI
    T ==> CartesianTensor(1,dim,K)
    Rep == Record(domain:NNI, codomain:NNI, data:T)
    rep(x:%):Rep == x pretend Rep
    per(x:Rep):% == x pretend %

    dom(f:%):NNI == rep(f).domain
    cod(f:%):NNI == rep(f).codomain

    dat(f:%):T == rep(f).data

    coerce(f:%):Prop(NNI) == dom(f)/cod(f)

    0 == per [0,0,0]

    --
    -- f+g : A^{n+m} -> A^p = f:A^n -> A^p + g:A^m -> A^p
    --
    (f:% + g:%):% ==
      dom(f) ~= dom(g) or cod(f) ~= cod(g) => error "arity"
      per [dom(f),cod(f),dat(f)+dat(g)]

    (f:% - g:%):% ==
      dom(f) ~= dom(f) or cod(g) ~= cod(g) => error "arity"
      per [dom(f),cod(f),dat(f)-dat(g)]

    --
    -- f/g : A^n -> A^p = f:A^n -> A^m / g:A^m -> A^p
    -- g*f : A^n -> A^p = g:A^m -> A^p * f:A^n -> A^m
    --
    (g:% * f:%):% ==
      cod(f) ~= dom(g) => error "arity"
      r:T := product(dat(f), dat(g))
      n:=dom(f)+1
      m:=n+cod(f)
      while m>n repeat
        r := contract(r,n,m)
        m:=m-1
      per [dom f,cod g,r]

    1:% == per [1,1,kroneckerDelta()$T]

    -- repeated composition
    (f:% ^ p:NNI):% ==
      cod(f) ~= dom(f) => error "arity"
      q:=subtractIfCan(p,1)
      q case NNI => f^q * f
      1

    -- repeated sum
    (f:% * p:NNI):% ==
      q:=subtractIfCan(p,1)
      q case NNI => f*q + f
      0

    (x:% = y:%):Boolean ==
      dom(x) ~= dom(y) or cod(x) ~= cod(y) => error "arity"
      dat(x) = dat(y)

    (x:K * y:%):% == per [dom(y),cod(y),x*dat(y)]

    (x:% * y:K):% == per [dom(x),cod(x),dat(x)*y]

    inp(x:List K):% == per [1,0,entries(x)::T]

    inp(x:List %):% ==
      #removeDuplicates([dom(y) for y in x])~=1 or
        #removeDuplicates([cod(y) for y in x])~=1 => error "arity"
      per [dom(first x)+1,cod(first x),[dat(y) for y in x]::T]$Rep

    out(x:List K):% == per [0,1,entries(x)::T]

    out(x:List %):% ==
      #removeDuplicates([dom(y) for y in x])~=1 or
        #removeDuplicates([cod(y) for y in x])~=1 => error "arity"
      per [dom(first x),cod(first x)+1,[dat(y) for y in x]::T]$Rep

    coerce(x:%):OutputForm == (dat(x))::OutputForm

   Compiling FriCAS source code from file 
      /var/zope2/var/LatexWiki/4431927989007062318-25px003.spad using 
      old system compiler.
   LIN abbreviates domain LinearOperator 
------------------------------------------------------------------------
   initializing NRLIB LIN for LinearOperator 
   compiling into NRLIB LIN 
   importing List NonNegativeInteger
   processing macro definition T$ ==> CartesianTensor(One,dim,K) 
   compiling local rep : $ -> Record(domain: NonNegativeInteger,codomain: NonNegativeInteger,data: CartesianTensor(One,dim,K))
      LIN;rep is replaced by x 
Time: 0.06 SEC.

   compiling local per : Record(domain: NonNegativeInteger,codomain: NonNegativeInteger,data: CartesianTensor(One,dim,K)) -> $
      LIN;per is replaced by x 
Time: 0 SEC.

   compiling exported dom : $ -> NonNegativeInteger
Time: 0 SEC.

   compiling exported cod : $ -> NonNegativeInteger
Time: 0 SEC.

   compiling local dat : $ -> CartesianTensor(One,dim,K)
Time: 0.01 SEC.

   compiling exported coerce : $ -> Prop NonNegativeInteger
Time: 0 SEC.

   compiling exported Zero : () -> $
Time: 0 SEC.

   compiling exported + : ($,$) -> $
Time: 0 SEC.

   compiling exported - : ($,$) -> $
Time: 0.01 SEC.

   compiling exported * : ($,$) -> $
Time: 0.01 SEC.

   compiling exported One : () -> $
Time: 0 SEC.

   compiling exported ^ : ($,NonNegativeInteger) -> $
Time: 0.01 SEC.

   compiling exported * : ($,NonNegativeInteger) -> $
Time: 0.01 SEC.

   compiling exported = : ($,$) -> Boolean
Time: 0.01 SEC.

   compiling exported * : (K,$) -> $
Time: 0 SEC.

   compiling exported * : ($,K) -> $
Time: 0 SEC.

   compiling exported inp : List K -> $
Time: 0.05 SEC.

   compiling exported inp : List $ -> $
Time: 0.08 SEC.

   compiling exported out : List K -> $
Time: 0 SEC.

   compiling exported out : List $ -> $
Time: 0.16 SEC.

   compiling exported coerce : $ -> OutputForm
Time: 0.01 SEC.

(time taken in buildFunctor:  0)

;;;     ***       |LinearOperator| REDEFINED

;;;     ***       |LinearOperator| REDEFINED
Time: 0.01 SEC.

   Cumulative Statistics for Constructor LinearOperator
      Time: 0.43 seconds

   finalizing NRLIB LIN 
   Processing LinearOperator for Browser database:
--------(inp (% (List K)))---------
--->-->LinearOperator((inp (% (List %)))): Not documented!!!!
--------(out (% (List K)))---------
--->-->LinearOperator((out (% (List %)))): Not documented!!!!
--->-->LinearOperator((coerce (% (SquareMatrix dim K)))): Not documented!!!!
--->-->LinearOperator((* (% % (NonNegativeInteger)))): Not documented!!!!
--->-->LinearOperator(constructor): Not documented!!!!
--->-->LinearOperator(): Missing Description
; compiling file "/var/zope2/var/LatexWiki/LIN.NRLIB/LIN.lsp" (written 09 APR 2011 07:57:51 AM):

; /var/zope2/var/LatexWiki/LIN.NRLIB/LIN.fasl written
; compilation finished in 0:00:00.371
------------------------------------------------------------------------
   LinearOperator is now explicitly exposed in frame initial 
   LinearOperator will be automatically loaded when needed from 
      /var/zope2/var/LatexWiki/LIN.NRLIB/LIN

   >> System error:
   The bounding indices 163 and 162 are bad for a sequence of length 162.
See also:
  The ANSI Standard, Glossary entry for "bounding index designator"
  The ANSI Standard, writeup for Issue SUBSEQ-OUT-OF-BOUNDS:IS-AN-ERROR

Construction operators: input and output

L:=LIN(2,FRAC POLY INT)

(1)

A1:L:=inp[script(a,[[1,i]]) for i in 1..2]

(2)

arity A1

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
               LinearOperator(2,Fraction(Polynomial(Integer)))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
A2:L:=inp[script(a,[[2,i]]) for i in 1..2]

(3)

A:L:=inp[A1,A2]

(4)

arity A

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
               LinearOperator(2,Fraction(Polynomial(Integer)))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
B1:L:=out[script(b,[[],[1,i]]) for i in 1..2]

(5)

arity B1

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
               LinearOperator(2,Fraction(Polynomial(Integer)))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
B2:L:=out[script(b,[[],[2,i]]) for i in 1..2]

(6)

B:L:=out[B1,B2]

(7)

arity B

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
               LinearOperator(2,Fraction(Polynomial(Integer)))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Composition

AB2 := A2 / B2; AB2::OutputForm = A2::OutputForm / B2::OutputForm

(8)

arity(AB2)::OutputForm = arity(A2)::OutputForm / arity(B2)::OutputForm

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
               LinearOperator(2,Fraction(Polynomial(Integer)))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
BA1 := B1 / A1; BA1::OutputForm = B1::OutputForm / A1::OutputForm

(9)

arity(BA1)::OutputForm = arity(B1)::OutputForm / arity(A1)::OutputForm

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
               LinearOperator(2,Fraction(Polynomial(Integer)))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
AB1 := A1 / B1; AB1::OutputForm = A1::OutputForm / B1::OutputForm

(10)

arity(AB1)::OutputForm = arity(A1)::OutputForm / arity(B1)::OutputForm

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
               LinearOperator(2,Fraction(Polynomial(Integer)))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Powers

AB3:=(AB1/AB1)/AB1

(11)

arity(AB3)

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
               LinearOperator(2,Fraction(Polynomial(Integer)))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
test(AB3=AB1/(AB1/AB1))

(12)

test(AB3=AB1^3)

(13)

B3p:=(B1*B1)*B1

   >> Error detected within library code:
   arity

Sums

A12s := A1 + A2; A12s::OutputForm = A1::OutputForm + A2::OutputForm

(14)

arity(A12s)::OutputForm = arity(A1)::OutputForm + arity(A2)::OutputForm

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
               LinearOperator(2,Fraction(Polynomial(Integer)))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
B12s := B1 + B2; B12s::OutputForm = B1::OutputForm + B2::OutputForm

(15)

arity(B12s)::OutputForm = arity(B1)::OutputForm + arity(B2)::OutputForm

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
               LinearOperator(2,Fraction(Polynomial(Integer)))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Multiplication

A3s:=(A1+A1)+A1

(16)

arity(A3s)

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
               LinearOperator(2,Fraction(Polynomial(Integer)))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
test(A3s=A1+(A1+A1))

(17)

test(A3s=A1*3)

   >> Error detected within library code:
   arity

B3s:=(B1+B1)+B1

(18)

arity(B3s)

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
               LinearOperator(2,Fraction(Polynomial(Integer)))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
test(B3s=B1+(B1+B1))

(19)

test(B3s=B1*3)

   >> Error detected within library code:
   arity

Expected error

B1A1:=B1*A1

(20)

arity(B1A1)

   There are 1 exposed and 0 unexposed library operations named arity 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op arity
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named arity
      with argument type(s) 
               LinearOperator(2,Fraction(Polynomial(Integer)))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Composition

AB11:=A1 B1

   Internal Error
   The function elt with signature hashcode is missing from domain 
      LinearOperator2(Fraction (Polynomial (Integer)))

Multiple inputs and outputs

W:L:=out[inp[inp([script(w,[[i,j],[k]]) for j in 1..2])$L for i in 1..2] for k in 1..2]

(21)

WB1:=W B1

   Internal Error
   The function elt with signature hashcode is missing from domain 
      LinearOperator2(Fraction (Polynomial (Integer)))

  ___ _       _        _  _
  ___ _)  =   _\_ _    _\/_
  _/          ___ _)   _/\_

  Rep == Record(Dom:VectorSpace, Cod:VectorSpace, t:T)

But VectorSpace? is a category which would make Dom and Cod domains. The domains that currently satisfy VectorSpace? in Axiom are rather limited and seem oddly focused on number theory (finite fields). It is a good thing however that DirectProduct? is a conditional member of this cateogry.

DirectProduct(2,FRAC INT) has VectorSpace(FRAC INT)

(22)

Unfortunately:

DirectProduct(2,DirectProduct(2,FRAC INT)) has VectorSpace(FRAC INT)

(23)

The problem with VectorSpace? is that the domain [Vector]? is not a member of this category instead it satisfies VectoryCategory?.

Is it possible to treat tensors from CartesianTensor? as maps from VectorSpace? to VectorSpace?? We would like for example:

  T:DirectProduct(dim,DirectProduct(dim,FRAC INT)) -> DirectProduct(dim,FRAC INT))

To be a linear operator with two inputs and one output.

FreeModule(Fraction Integer,OrderedVariableList [e1,e1]) has VectorSpace(Fraction Integer)

(24)