4-dimensional vector space representing Quaternion algebra
axiom
dim:=4
axiom
T := CartesianTensor(1,dim,EXPR INT)
Type: Type
axiom
X:List T := [unravel [(i=j => 1;0) for j in 1..dim] for i in 1..dim]
Type: List(CartesianTensor
?(1,
4,
Expression(Integer)))
axiom
X(1),X(2)
Type: Tuple(CartesianTensor
?(1,
4,
Expression(Integer)))
Generate structure constants for Quaternion Algebra
axiom
B:=map(x+->quatern(x.1,x.2,x.3,x.4),1$SQMATRIX(4,FRAC INT)::List List FRAC INT)
Type: List(Quaternion(Fraction(Integer)))
axiom
M:=matrix [[B.i*B.j for j in 1..4] for i in 1..4]
Type: Matrix(Quaternion(Fraction(Integer)))
axiom
S(y)==map(x+->(x*inv(y)=1 or x*inv(y)=-1 => x*inv(y);0),M)
Type: Void
axiom
Yg:T:=unravel concat concat(map(S,B)::List List List FRAC POLY INT)
axiom
Compiling function S with type Quaternion(Fraction(Integer)) ->
Matrix(Quaternion(Fraction(Integer)))Type: CartesianTensor
?(1,
4,
Expression(Integer))
A scalar product is denoted by the (2,0)-tensor
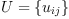
axiom
U:T := unravel(concat
[[script(u,[[],[j,i]])
for i in 1..dim]
for j in 1..dim]
)
Type: CartesianTensor
?(1,
4,
Expression(Integer))
Definition 1
We say that the scalar product is associative if the tensor
equation holds:
Y = Y
U U
In other words, if the (3,0)-tensor:
i j k i j k i j k
\ | / \/ / \ \/
\|/ = \ / - \ /
0 0 0
(three-point function) is zero.
axiom
ω := reindex(reindex(U,[2,1])*reindex(Yg,[1,3,2]),[3,2,1])-U*Yg
Type: CartesianTensor
?(1,
4,
Expression(Integer))
Definition 2
An algebra with a non-degenerate associative scalar product
is called pre-Frobenius.
We may consider the problem where multiplication Y is given,
and look for all associative scalar products 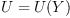
This problem can be solved using linear algebra.
axiom
)expose MCALCFN
MultiVariableCalculusFunctions is now explicitly exposed in frame
initial
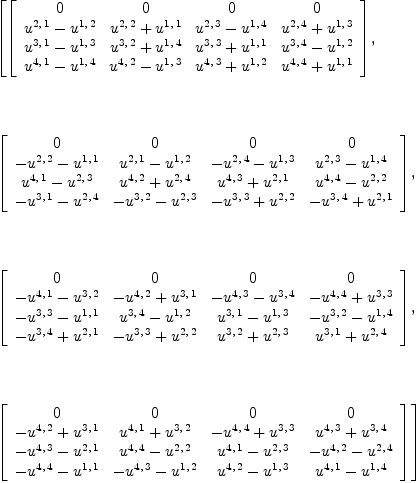
J := jacobian(ravel ω,concat(map(variables,ravel U))::List Symbol);
Type: Matrix(Expression(Integer))
axiom
uu := transpose matrix [concat(map(variables,ravel(U)))::List Symbol];
Type: Matrix(Polynomial(Integer))
axiom
J::OutputForm * uu::OutputForm = 0
Type: Equation(OutputForm
?)
axiom
nrows(J)
axiom
ncols(J)
The matrix J transforms the coefficients of the tensor 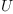 into coefficients of the tensor
into coefficients of the tensor 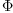 . We are looking for
the general linear family of tensors
. We are looking for
the general linear family of tensors 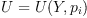 such that
such that
J transforms 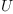 into
into 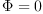 for any such
for any such 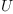 .
.
If the null space of the J matrix is not empty we can use
the basis to find all non-trivial solutions for U:
axiom
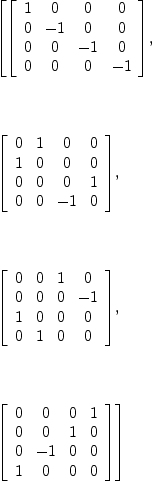
NJ:=nullSpace(J)
Type: List(Vector(Expression(Integer)))
axiom
SS:=map((x,y)+->x=y,concat map(variables,ravel U),
entries reduce(+,[p[i]*NJ.i for i in 1..#NJ]))
Type: List(Equation(Expression(Integer)))
axiom
Ug:T := unravel(map(x+->subst(x,SS),ravel U))
Type: CartesianTensor
?(1,
4,
Expression(Integer))
This defines a family of pre-Frobenius algebras:
axiom
test(unravel(map(x+->subst(x,SS),ravel ω))$T=0*ω)
Type: Boolean
The scalar product must be non-degenerate:
axiom
Ud:DMP([p[i] for i in 1..#NJ],INT) := determinant [[Ug[i,j] for j in 1..dim] for i in 1..dim]
Type: DistributedMultivariatePolynomial
?([*01p1,
*01p2,
*01p3,
*01p4],
Integer)
axiom
factor Ud
Type: Factored(DistributedMultivariatePolynomial
?([*01p1,
*01p2,
*01p3,
*01p4],
Integer))
Definition 3
Co-pairing
axiom
Ωg:T:=unravel concat(transpose(1/Ud*adjoint([[Ug[i,j] for j in 1..dim] for i in 1..dim]).adjMat)::List List FRAC POLY INT)
Type: CartesianTensor
?(1,
4,
Expression(Integer))
dimension
Ω
U
axiom
contract(contract(Ωg,1,Ug,1),1,2)
Type: CartesianTensor
?(1,
4,
Expression(Integer))
Definition 4
Co-multiplication
axiom
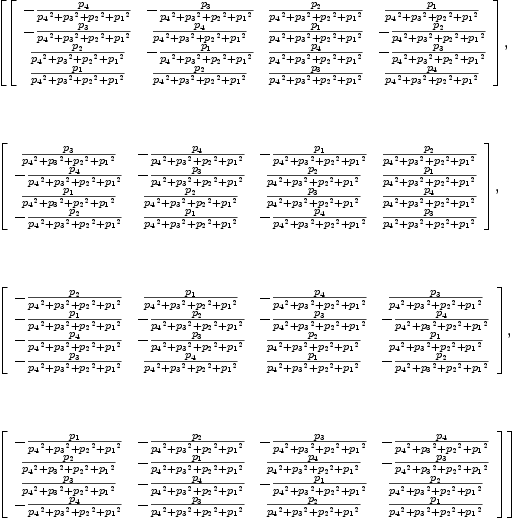
λg:=reindex(contract(contract(Ug*Yg,1,Ωg,1),1,Ωg,1),[2,3,1]);
Type: CartesianTensor
?(1,
4,
Expression(Integer))
axiom
-- just for display
reindex(λg,[3,1,2])
Type: CartesianTensor
?(1,
4,
Expression(Integer))
i
λ=Ω
axiom
test(λg*X(1)=Ωg)
Type: Boolean
Definition 5
Co-unit
i
U
axiom
ιg:=X(1)*Ug
Type: CartesianTensor
?(1,
4,
Expression(Integer))
Y=U
ι
axiom
test(ιg * Yg = Ug)
Type: Boolean
For example:
axiom
Ug0:T:=unravel eval(ravel Ug,[p[1]=1,p[2]=0,p[3]=0,p[4]=1])
Type: CartesianTensor
?(1,
4,
Expression(Integer))
axiom
Ωg0:T:=unravel eval(ravel Ωg,[p[1]=1,p[2]=0,p[3]=0,p[4]=1])
Type: CartesianTensor
?(1,
4,
Expression(Integer))
axiom
λg0:T:=unravel eval(ravel λg,[p[1]=1,p[2]=0,p[3]=0,p[4]=1]);
Type: CartesianTensor
?(1,
4,
Expression(Integer))
axiom
reindex(λg0,[3,1,2])
Type: CartesianTensor
?(1,
4,
Expression(Integer))
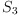 -permuted Frobenius Algebras
-permuted Frobenius Algebras
Zbigniew Oziewicz, Gregory Peter Wene
(26 Mar 2011)
http://arxiv.org/abs/1103.5113
axiom
test( Yg = reindex(reindex( reindex(Ug*Yg,[1,2,3]), [2,3,1])*Ωg,[3,1,2]) )
Type: Boolean
axiom
Yg213 := reindex(reindex( reindex(Ug*Yg,[2,1,3]), [2,3,1])*Ωg,[3,1,2]);
Type: CartesianTensor
?(1,
4,
Expression(Integer))
axiom
ω213 := reindex(reindex(U,[2,1])*reindex(Yg213,[1,3,2]),[3,2,1])-U*Yg213;
Type: CartesianTensor
?(1,
4,
Expression(Integer))
axiom
J213 := jacobian(ravel ω213,concat(map(variables,ravel U))::List Symbol);
Type: Matrix(Expression(Integer))
axiom
NJ213 := nullSpace(J213)
Type: List(Vector(Expression(Integer)))
axiom
-- opposite algebra
Yg132 := reindex(reindex( reindex(Ug*Yg,[1,3,2]), [2,3,1])*Ωg,[3,1,2]);
Type: CartesianTensor
?(1,
4,
Expression(Integer))
axiom
ω132 := reindex(reindex(U,[2,1])*reindex(Yg132,[1,3,2]),[3,2,1])-U*Yg132;
Type: CartesianTensor
?(1,
4,
Expression(Integer))
axiom
J132 := jacobian(ravel ω132,concat(map(variables,ravel U))::List Symbol);
Type: Matrix(Expression(Integer))
axiom
NJ132 := nullSpace(J132)
Type: List(Vector(Expression(Integer)))
axiom
Yg321 := reindex(reindex( reindex(Ug*Yg,[3,2,1]), [2,3,1])*Ωg,[3,1,2]);
Type: CartesianTensor
?(1,
4,
Expression(Integer))
axiom
ω321 := reindex(reindex(U,[2,1])*reindex(Yg321,[1,3,2]),[3,2,1])-U*Yg321;
Type: CartesianTensor
?(1,
4,
Expression(Integer))
axiom
J321 := jacobian(ravel ω321,concat(map(variables,ravel U))::List Symbol);
Type: Matrix(Expression(Integer))
axiom
NJ321 := nullSpace(J321)
Type: List(Vector(Expression(Integer)))
axiom
Yg312 := reindex(reindex( reindex(Ug*Yg,[3,1,2]), [2,3,1])*Ωg,[3,1,2]);
Type: CartesianTensor
?(1,
4,
Expression(Integer))
axiom
ω312 := reindex(reindex(U,[2,1])*reindex(Yg312,[1,3,2]),[3,2,1])-U*Yg312;
Type: CartesianTensor
?(1,
4,
Expression(Integer))
axiom
J312 := jacobian(ravel ω312,concat(map(variables,ravel U))::List Symbol);
Type: Matrix(Expression(Integer))
axiom
NJ312 := nullSpace(J312)
Type: List(Vector(Expression(Integer)))
axiom
Yg231 := reindex(reindex( reindex(Ug*Yg,[2,3,1]), [2,3,1])*Ωg,[3,1,2]);
Type: CartesianTensor
?(1,
4,
Expression(Integer))
axiom
ω231 := reindex(reindex(U,[2,1])*reindex(Yg231,[1,3,2]),[3,2,1])-U*Yg231;
Type: CartesianTensor
?(1,
4,
Expression(Integer))
axiom
J231 := jacobian(ravel ω231,concat(map(variables,ravel U))::List Symbol);
Type: Matrix(Expression(Integer))
axiom
NJ231 := nullSpace(J231)
Type: List(Vector(Expression(Integer)))
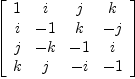
![]()
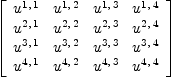
![]()

![]() into coefficients of the tensor
into coefficients of the tensor ![]() . We are looking for
the general linear family of tensors
. We are looking for
the general linear family of tensors ![]() such that
such that
![]() into
into ![]() for any such
for any such ![]() .
.![\label{eq14}\begin{array}{@{}l}
\displaystyle
\left[{\left[ 0, \: 0, \: 0, \: 1, \: 0, \: 0, \: 1, \: 0, \: 0, \: - 1, \: 0, \: 0, \: 1, \: 0, \: 0, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[ 0, \: 0, \: 1, \: 0, \: 0, \: 0, \: 0, \: - 1, \: 1, \: 0, \: 0, \: 0, \: 0, \: 1, \: 0, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[ 0, \: - 1, \: 0, \: 0, \: - 1, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: - 1, \: 0, \: 0, \: 1, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[ - 1, \: 0, \: 0, \: 0, \: 0, \: 1, \: 0, \: 0, \: 0, \: 0, \: 1, \: 0, \: 0, \: 0, \: 0, \: 1 \right]}\right]
\label{eq14}\begin{array}{@{}l}
\displaystyle
\left[{\left[ 0, \: 0, \: 0, \: 1, \: 0, \: 0, \: 1, \: 0, \: 0, \: - 1, \: 0, \: 0, \: 1, \: 0, \: 0, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[ 0, \: 0, \: 1, \: 0, \: 0, \: 0, \: 0, \: - 1, \: 1, \: 0, \: 0, \: 0, \: 0, \: 1, \: 0, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[ 0, \: - 1, \: 0, \: 0, \: - 1, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: - 1, \: 0, \: 0, \: 1, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[ - 1, \: 0, \: 0, \: 0, \: 0, \: 1, \: 0, \: 0, \: 0, \: 0, \: 1, \: 0, \: 0, \: 0, \: 0, \: 1 \right]}\right]](images/3676253141109063621-16.0px.png)
![\label{eq15}\begin{array}{@{}l}
\displaystyle
\left[{{u^{1, \: 1}}= -{p_{4}}}, \:{{u^{1, \: 2}}= -{p_{3}}}, \:{{u^{1, \: 3}}={p_{2}}}, \:{{u^{1, \: 4}}={p_{1}}}, \: \right.
\
\
\displaystyle
\left.{{u^{2, \: 1}}= -{p_{3}}}, \:{{u^{2, \: 2}}={p_{4}}}, \:{{u^{2, \: 3}}={p_{1}}}, \:{{u^{2, \: 4}}= -{p_{2}}}, \: \right.
\
\
\displaystyle
\left.{{u^{3, \: 1}}={p_{2}}}, \:{{u^{3, \: 2}}= -{p_{1}}}, \:{{u^{3, \: 3}}={p_{4}}}, \:{{u^{3, \: 4}}= -{p_{3}}}, \: \right.
\
\
\displaystyle
\left.{{u^{4, \: 1}}={p_{1}}}, \:{{u^{4, \: 2}}={p_{2}}}, \:{{u^{4, \: 3}}={p_{3}}}, \:{{u^{4, \: 4}}={p_{4}}}\right]
\label{eq15}\begin{array}{@{}l}
\displaystyle
\left[{{u^{1, \: 1}}= -{p_{4}}}, \:{{u^{1, \: 2}}= -{p_{3}}}, \:{{u^{1, \: 3}}={p_{2}}}, \:{{u^{1, \: 4}}={p_{1}}}, \: \right.
\
\
\displaystyle
\left.{{u^{2, \: 1}}= -{p_{3}}}, \:{{u^{2, \: 2}}={p_{4}}}, \:{{u^{2, \: 3}}={p_{1}}}, \:{{u^{2, \: 4}}= -{p_{2}}}, \: \right.
\
\
\displaystyle
\left.{{u^{3, \: 1}}={p_{2}}}, \:{{u^{3, \: 2}}= -{p_{1}}}, \:{{u^{3, \: 3}}={p_{4}}}, \:{{u^{3, \: 4}}= -{p_{3}}}, \: \right.
\
\
\displaystyle
\left.{{u^{4, \: 1}}={p_{1}}}, \:{{u^{4, \: 2}}={p_{2}}}, \:{{u^{4, \: 3}}={p_{3}}}, \:{{u^{4, \: 4}}={p_{4}}}\right]](images/4912796482163709487-16.0px.png)
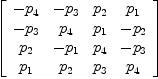
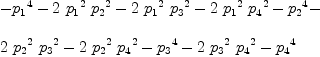
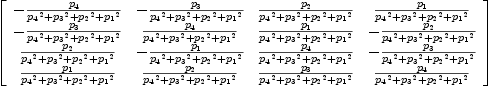



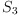 -permuted Frobenius Algebras
-permuted Frobenius Algebras![\label{eq31}\begin{array}{@{}l}
\displaystyle
\left[{\left[ 0, \: 0, \: 0, \: 1, \: 0, \: 0, \: - 1, \: 0, \: 0, \: 1, \: 0, \: 0, \: 1, \: 0, \: 0, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[ 0, \: 0, \: - 1, \: 0, \: 0, \: 0, \: 0, \: - 1, \: - 1, \: 0, \: 0, \: 0, \: 0, \: 1, \: 0, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[ 0, \: 1, \: 0, \: 0, \: 1, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: - 1, \: 0, \: 0, \: 1, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[ - 1, \: 0, \: 0, \: 0, \: 0, \: 1, \: 0, \: 0, \: 0, \: 0, \: 1, \: 0, \: 0, \: 0, \: 0, \: 1 \right]}\right]
\label{eq31}\begin{array}{@{}l}
\displaystyle
\left[{\left[ 0, \: 0, \: 0, \: 1, \: 0, \: 0, \: - 1, \: 0, \: 0, \: 1, \: 0, \: 0, \: 1, \: 0, \: 0, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[ 0, \: 0, \: - 1, \: 0, \: 0, \: 0, \: 0, \: - 1, \: - 1, \: 0, \: 0, \: 0, \: 0, \: 1, \: 0, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[ 0, \: 1, \: 0, \: 0, \: 1, \: 0, \: 0, \: 0, \: 0, \: 0, \: 0, \: - 1, \: 0, \: 0, \: 1, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[ - 1, \: 0, \: 0, \: 0, \: 0, \: 1, \: 0, \: 0, \: 0, \: 0, \: 1, \: 0, \: 0, \: 0, \: 0, \: 1 \right]}\right]](images/2939396497145074544-16.0px.png)