Edit detail for SandBox Quaternion Algebra is Frobenius in Many Ways revision 32 of 32

Quaternion Algebra Is Frobenius In Many Ways

Linear operators over a 4-dimensional vector space representing quaternion algebra

Ref:

• http://arxiv.org/abs/1103.5113

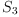  -permuted Frobenius Algebras

  Zbigniew Oziewicz (UNAM), Gregory Peter Wene (UTSA)

• http://mat.uab.es/~kock/TQFT.html

  Frobenius algebras and 2D topological quantum field theories

  Joachim Kock

• http://en.wikipedia.org/wiki/Frobenius_algebra

We need the Axiom LinearOperator library.

(1) -> )library CARTEN ARITY CMONAL CPROP CLOP CALEY

   CartesianTensor is now explicitly exposed in frame initial 
   CartesianTensor will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/CARTEN.NRLIB/CARTEN
   Arity is now explicitly exposed in frame initial 
   Arity will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/ARITY.NRLIB/ARITY
   ClosedMonoidal is now explicitly exposed in frame initial 
   ClosedMonoidal will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/CMONAL.NRLIB/CMONAL
   ClosedProp is now explicitly exposed in frame initial 
   ClosedProp will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/CPROP.NRLIB/CPROP
   ClosedLinearOperator is now explicitly exposed in frame initial 
   ClosedLinearOperator will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/CLOP.NRLIB/CLOP
   CaleyDickson is now explicitly exposed in frame initial 
   CaleyDickson will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/CALEY.NRLIB/CALEY

Use the following macros for convenient notation

-- summation
macro Σ(x,i,n)==reduce(+,[x for i in n])

-- subscript and superscripts
macro sb == subscript

macro sp == superscript

ℒ is the domain of 4-dimensional linear operators over the rational functions ℚ (Expression Integer), i.e. ratio of polynomials with integer coefficients.

dim:=4

(1)

macro ℂ == CaleyDickson

macro ℚ == Expression Integer

ℒ := ClosedLinearOperator(OVAR ['1,'i,'j,'k], ℚ)

(2)

ⅇ:List ℒ      := basisOut()

(3)

ⅆ:List ℒ      := basisIn()

(4)

I:ℒ:=[1]   -- identity for composition

(5)

X:ℒ:=[2,1] -- twist

(6)

V:ℒ:=ev(1) -- evaluation

(7)

Λ:ℒ:=co(1) -- co-evaluation

(8)

equate(eq)==map((x,y)+->(x=y),ravel lhs eq, ravel rhs eq);

Now generate structure constants for Quaternion Algebra

The basis consists of the real and imaginary units. We use quaternion multiplication to form the "multiplication table" as a matrix. Then the structure constants can be obtained by dividing each matrix entry by the list of basis vectors.

Split-complex and co-quaternions can be specified by Caley-Dickson parameters (i2, j2)

i2:=sp('i,[2])

(9)

--i2:= -1  -- complex
j2:=sp('j,[2])

(10)

--j2:= -1  -- quaternion
k2:=-i2*j2;

QQ := ℂ(ℂ(ℚ,'i,-i2),'j,-j2);

   Cannot convert the value from type Polynomial(Integer) to 
      CaleyDickson(Expression(Integer),i,-(i[;2])) .

Basis: Each B.i is a quaternion number

B:List QQ := map(x +-> hyper x,1$SQMATRIX(dim,ℚ)::List List ℚ)

   QQ is not a valid type.

Units

q:=ⅇ.1; i:=ⅇ.2; j:=ⅇ.3; k:=ⅇ.4;

Multiplication of arbitrary quaternions and

a:=Σ(sb('a,[i])*ⅇ.i, i,1..dim)

(11)

b:=Σ(sb('b,[i])*ⅇ.i, i,1..dim)

(12)

(a*b)/Y

                   0 0
                  -- -
                   2 0
                  +
   arity warning: ----
                   2
                  +  0
                  -- -
                   2 0
                  +

(13)

Multiplication is Associative

test(
  ( I Y ) / _
  (  Y  ) = _
  ( Y I ) / _
  (  Y  ) )

                  + 0
                  - -
                  + 0
   arity warning: ---
                  + 0
                  - -
                  + 0
   There are no exposed library operations named Y but there are 2 
      unexposed operations with that name. Use HyperDoc Browse or issue
                                )display op Y
      to learn more about the available operations.

   Cannot find a definition or applicable library operation named Y 
      with argument type(s) 
  ClosedLinearOperator(OrderedVariableList([1,i,j,k]),Expression(Integer))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

A scalar product is denoted by the (2,0)-tensor

U:=Σ(Σ(script('u,[[],[i,j]])*ⅆ.i*ⅆ.j, i,1..dim), j,1..dim)

(14)

Definition 1

We say that the scalar product is associative if the tensor equation holds:

    Y   =   Y
     U     U

In other words, if the (3,0)-tensor:

(15)

Using the LinearOperator domain in Axiom and some carefully chosen symbols we can easily enter expressions that are both readable and interpreted by Axiom as "graphical calculus" diagrams describing complex products and compositions of linear operators.

ω:ℒ :=
     (    Y I    )  /
           U        -
     (    I Y    )  /
           U

   There are no exposed library operations named Y but there are 2 
      unexposed operations with that name. Use HyperDoc Browse or issue
                                )display op Y
      to learn more about the available operations.

   Cannot find a definition or applicable library operation named Y 
      with argument type(s) 
  ClosedLinearOperator(OrderedVariableList([1,i,j,k]),Expression(Integer))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Definition 2

An algebra with a non-degenerate associative scalar product is called a [Frobenius Algebra]?.

The Cartan-Killing Trace

Ú:=
   (  Y Λ  ) / _
   (   Y I ) / _
        V

   There are no exposed library operations named Y but there are 2 
      unexposed operations with that name. Use HyperDoc Browse or issue
                                )display op Y
      to learn more about the available operations.

   Cannot find a definition or applicable library operation named Y 
      with argument type(s) 
  ClosedLinearOperator(OrderedVariableList([1,i,j,k]),Expression(Integer))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

forms a non-degenerate associative scalar product for Y

Ũ := Ù

(16)

test
     (    Y I    )  /
           Ũ        =
     (    I Y    )  /
           Ũ

   There are no exposed library operations named Y but there are 2 
      unexposed operations with that name. Use HyperDoc Browse or issue
                                )display op Y
      to learn more about the available operations.

   Cannot find a definition or applicable library operation named Y 
      with argument type(s) 
  ClosedLinearOperator(OrderedVariableList([1,i,j,k]),Expression(Integer))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

General Solution

We may consider the problem where multiplication Y is given, and look for all associative scalar products

This problem can be solved using linear algebra.

)expose MCALCFN

   MultiVariableCalculusFunctions is now explicitly exposed in frame 
      initial 
J := jacobian(ravel ω,concat map(variables,ravel U)::List Symbol);

nrows(J),ncols(J)

(17)

The matrix J transforms the coefficients of the tensor into coefficients of the tensor . We are looking for the general linear family of tensors such that J transforms into for any such .

If the null space of the J matrix is not empty we can use the basis to find all non-trivial solutions for U:

Ñ:=nullSpace(J)

(18)

ℰ:=map((x,y)+->x=y, concat
       map(variables,ravel U), entries Σ(sb('p,[i])*Ñ.i, i,1..#Ñ) )

(19)

This defines a family of pre-Frobenius algebras:

zero? eval(ω,ℰ)

(20)

Ų:ℒ := eval(U,ℰ)

(21)

Frobenius Form (co-unit)

d:=ε1*ⅆ.1+εi*ⅆ.2+εj*ⅆ.3+εk*ⅆ.4

(22)

equate(d=
    (    q I   ) / _
          Ų    )

Compiling function equate with type Equation(ClosedLinearOperator(
      OrderedVariableList([1,i,j,k]),Expression(Integer))) -> List(
      Equation(Expression(Integer)))

(23)

Express scalar product in terms of Frobenius form

Ξ:=solve(%,[sb('p,[i]) for i in 1..#Ñ]).1

   >> Error detected within library code:
   system does not have a finite number of solutions

In general the pairing is not symmetric!

u1:=matrix [[retract((ⅇ.i ⅇ.j)/Ų) for i in 1..dim] for j in 1..dim]

(24)

The scalar product must be non-degenerate:

Ů:=determinant u1

(25)

factor(numer Ů)/factor(denom Ů)

(26)

Cartan-Killing is a special case

ck:=solve(equate(eval(Ũ,Ξ)=Ų),[ε1,εi,εj,εk]).1

   There are 10 exposed and 6 unexposed library operations named eval 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op eval
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named eval 
      with argument type(s) 
                                 Variable(Ù)
                                 Variable(Ξ)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Frobenius scalar product of "vector" quaternions and

a:=sb('a,[1])*i+sb('a,[2])*j

(27)

b:=sb('b,[1])*i+sb('b,[2])*j

(28)

(a,a)/Ų

(29)

(b,b)/Ų

(30)

(a,b)/Ų

(31)

Definition 3

Co-scalar product

Solve the Snake Relation as a system of linear equations.

Ω:ℒ:=Σ(Σ(script('u,[[i,j]])*ⅇ.i*ⅇ.j, i,1..dim), j,1..dim)

(32)

ΩX:=Ω/X;

UXΩ:=(I*ΩX)/(Ų*I);

ΩXU:=(ΩX*I)/(I*Ų);

eq1:=equate(UXΩ=I);

eq2:=equate(ΩXU=I);

snake:=solve(concat(eq1,eq2),concat [[script('u,[[i,j]]) for i in 1..dim] for j in 1..dim]);

if #snake ~= 1 then error "no solution"

Ω:=eval(Ω,snake(1))

(33)

ΩX:=Ω/X;

The common demoninator is

squareFreePart factor denom Ů / squareFreePart factor numer Ů

Function:  squareFree : % -> Factored(%) is missing from domain: Factored(SparseMultivariatePolynomial(Integer,Kernel(Expression(Integer))))
   Internal Error
   The function squareFree with signature (Factored %) is missing from 
      domain Factored
      (SparseMultivariatePolynomial (Integer) (Kernel (Expression (Integer))))

Check "dimension" and the snake relations.

O:ℒ:=
       Ω    /
       Ų

(34)

test
    (    I ΩX     )  /
    (     Ų I     )  =  I

(35)

test
    (     ΩX I    )  /
    (    I Ų      )  =  I

(36)

Cartan-Killing co-scalar

eval(Ω,ck)

   There are 10 exposed and 6 unexposed library operations named eval 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op eval
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named eval 
      with argument type(s) 
  ClosedLinearOperator(OrderedVariableList([1,i,j,k]),Expression(Integer))
                                Variable(ck)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Definition 4

Co-algebra

Compute the "three-point" function and use it to define co-multiplication.

W:=
  (Y I) /
    Ų

   There are no exposed library operations named Y but there are 2 
      unexposed operations with that name. Use HyperDoc Browse or issue
                                )display op Y
      to learn more about the available operations.

   Cannot find a definition or applicable library operation named Y 
      with argument type(s) 
  ClosedLinearOperator(OrderedVariableList([1,i,j,k]),Expression(Integer))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Cartan-Killing co-multiplication

eval(λ,ck)

   There are 10 exposed and 6 unexposed library operations named eval 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op eval
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named eval 
      with argument type(s) 
                                 Variable(λ)
                                Variable(ck)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

test
     (    I ΩX     )  /
     (     Y I     )  =  λ

   There are no exposed library operations named Y but there are 2 
      unexposed operations with that name. Use HyperDoc Browse or issue
                                )display op Y
      to learn more about the available operations.

   Cannot find a definition or applicable library operation named Y 
      with argument type(s) 
  ClosedLinearOperator(OrderedVariableList([1,i,j,k]),Expression(Integer))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Co-associativity

test(
  (  λ  ) / _
  ( I λ ) = _
  (  λ  ) / _
  ( λ I ) )

                  0 +
                  - -
                  0 +
   arity warning: ---
                  0 +
                  - -
                  0 +
   There are no library operations named λ 
      Use HyperDoc Browse or issue
                                 )what op λ
      to learn if there is any operation containing " λ " in its name.

   Cannot find a definition or applicable library operation named λ 
      with argument type(s) 
  ClosedLinearOperator(OrderedVariableList([1,i,j,k]),Expression(Integer))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

test
         q     /
         λ     =    ΩX

                  0 0
                  - -
                  + 0
   arity warning: ---
                  + 0
                  - -
                  + 0

(37)

Frobenius Condition (fork)

H :=
         Y    /
         λ

(38)

test
     (   λ I   )  /
     (  I Y    )  =  H

   There are no library operations named λ 
      Use HyperDoc Browse or issue
                                 )what op λ
      to learn if there is any operation containing " λ " in its name.

   Cannot find a definition or applicable library operation named λ 
      with argument type(s) 
  ClosedLinearOperator(OrderedVariableList([1,i,j,k]),Expression(Integer))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

The Cartan-Killing form makes H of the Frobenius condition idempotent

test( eval(H,ck)=eval(H/H,ck) )

   There are 10 exposed and 6 unexposed library operations named eval 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op eval
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named eval 
      with argument type(s) 
                        Fraction(Polynomial(Integer))
                                Variable(ck)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

But it is not unique. E.g. other idempots

h1:=map(numer,ravel(H-H/H)::List FRAC POLY INT);

   There are 2 exposed and 0 unexposed library operations named ravel 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op ravel
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named ravel
      with argument type(s) 
                        Fraction(Polynomial(Integer))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Handle and handle element

Φ :=
         λ     /
         Y

(39)

Φ1 :=    q     /
         Φ

                  0 0
                  - -
                  + 0
   arity warning: ---
                  + 0
                  - -
                  + 0

(40)

The Cartan-Killing form makes Φ into the identity

test( eval(Φ,ck)=I )

   There are 10 exposed and 6 unexposed library operations named eval 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op eval
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named eval 
      with argument type(s) 
                        Fraction(Polynomial(Integer))
                                Variable(ck)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

but it can be the identity in many ways. For example,

solve(equate(eval(Φ,[ε1=1,εi=1,εj=1,j2=-1])=I),[εk])

(41)

If handle is identity then fork is idempotent but the converse is not true

Φ1:=map(numer,ravel(Φ-I)::List FRAC POLY INT);

   >> Error detected within library code:
   Rank mismatch

Figure 12

φφ:=          _
  ( Ω  Ω  ) / _
  ( X I I ) / _
  ( I X I ) / _
  ( I I X ) / _
  (  Y  Y );

   There are no exposed library operations named Y but there are 2 
      unexposed operations with that name. Use HyperDoc Browse or issue
                                )display op Y
      to learn more about the available operations.

   Cannot find a definition or applicable library operation named Y 
      with argument type(s) 
                                 Variable(Y)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

For Cartan-Killing this is just the co-scalar

test(eval(φφ,ck)=eval(Ω,ck))

   There are 10 exposed and 6 unexposed library operations named eval 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op eval
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named eval 
      with argument type(s) 
                                Variable(φφ)
                                Variable(ck)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Bi-algebra conditions

ΦΦ:=          _
  (  λ λ  ) / _
  ( I I X ) / _
  ( I X I ) / _
  ( I I X ) / _
  (  Y  Y ) ;

   There are no library operations named λ 
      Use HyperDoc Browse or issue
                                 )what op λ
      to learn if there is any operation containing " λ " in its name.

   Cannot find a definition or applicable library operation named λ 
      with argument type(s) 
                                 Variable(λ)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Theorem 8.3

u2:=map(retract,matrix [ _
        [q/d,     i/d,    j/d,     k/d], _
        [i/d,  i2*q/d,    k/d,  i2*j/d], _
        [j/d,    -k/d, j2*q/d, -j2*i/d], _
        [k/d, -i2*j/d, j2*i/d, k2*q/d]])

(42)

test(u2=transpose(u1))

(43)

Ů2 := -retract( k2*(q/d)^2 + j2*(i/d)^2 + i2*(j/d)^2 - (k/d)^2 )^2

(44)

factor(numer Ů2)/factor(denom Ů2)

(45)

test(Ů=Ů2)

(46)