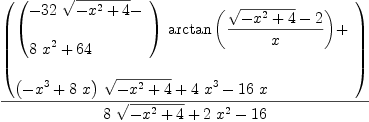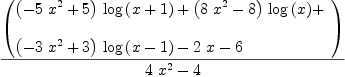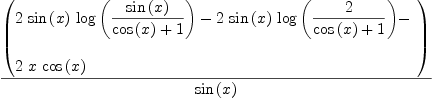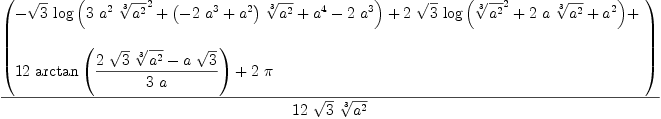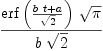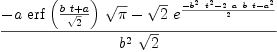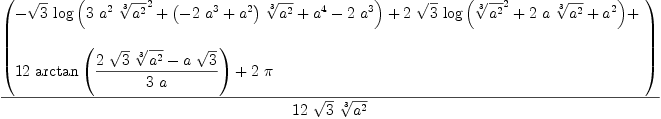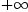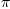Edit detail for SandBox Integration revision 2 of 19

Integration

Let's do some integration examples:

integrate(%e**x, x)

(1)

Type: Union(Expression(Integer),...)

load_package SPECFN;

on ROUNDED,ADJPREC;

Ei(1.00000000000000000001);
*** precision increased to 21

Ei(1.0);

Ei(2.0);

Can Reduce compute Ei in arbitrary precision?

See http://www.uni-koeln.de/REDUCE/3.6/doc/specfn/

Also http://homepages.inf.ed.ac.uk/mtoussai/publications/toussaint-99-mexico.pdf

Reset

off ROUNDED,ADJPREC;

int(cos(x),x,0,pi);

*** ci already defined as operator 

*** si already defined as operator

integrate(x^2/sqrt(4-x^2),x)

(2)

Type: Union(Expression(Integer),...)

integrate(exp(-a*x**2),x=0..%plusInfinity)

(3)

Type: Union(fail: failed,...)

The following won't "work", see CommonMistakes?:

integrate(exp(-a::PositiveInteger*x**2),x=0..%plusInfinity)

   Cannot convert from type Variable(a) to PositiveInteger for value
   a

integrate((x^3+x^2+2)/(x*(x^2-1)^2), x)

(4)

Type: Union(Expression(Integer),...)

integrate(2*x/sin(x)^2,x)

(5)

Type: Union(Expression(Integer),...)

Comparing Axiom and Reduce:

integrate(sin(1/x),x)

(6)

Type: Union(Expression(Integer),...)

int(sin(1/x),x);

Hell, why does the following blow MathAction??:

  \begin{reduce}
  load_package algint;
  int(sin(1/x),x);
  \end{reduce}

A different problem, where Axiom has to give up:

integrate(sqrt(sin(1/x)),x)

   >> Error detected within library code:
   integrate: implementation incomplete (constant residues)

However, in Reduce: Again, why does the following blow MathAction??:

  \begin{reduce}
  load_package algint;
  int(sqrt(sin(1/x)),x);
  \end{reduce}

integrate(exp(-x^2),x)

(7)

Type: Union(Expression(Integer),...)

integrate(sin(x)/x,x)

(8)

Type: Union(Expression(Integer),...)

differentiate(%,x)

(9)

Type: Expression(Integer)

integrate(sin(1/x),x=%minusInfinity..%plusInfinity,"noPole")

   >> Error detected within library code:
   integrate: pole in path of integration

integrate(2*x/sin(x)^2,x=1/2..1);

Type: Union(pole: potentialPole,...)

integrate(sin(x),x=0..%pi/2)

(10)

Type: Union(f1: OrderedCompletion(Expression(Integer)),...)

integrate(atan(x/a)/x,x)

(11)

Type: Union(Expression(Integer),...)

integrate(1/(a+z^3), z=0..1,"noPole")

(12)

Type: Union(f1: OrderedCompletion(Expression(Integer)),...)

integrate(x^3+x^2/4+x,x)

(13)

Type: Polynomial(Fraction(Integer))

You cannot integrate Expression Float

integrate(50*%e^(-0.02*t),t)

   There are 11 exposed and 8 unexposed library operations named
      integrate having 2 argument(s) but none was determined to be
      applicable. Use HyperDoc Browse, or issue
                            )display op integrate
      to learn more about the available operations. Perhaps
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named
      integrate with argument type(s)
                              Expression(Float)
                                 Variable(t)

      Perhaps you should use "@" to indicate the required return type,
      or "$" to specify which version of the function you need.

But symbolic integration works with integer expressions

integrate(50*%e^(-0.02*t)::Expression Fraction Integer,t)

(14)

Type: Union(Expression(Fraction(Integer)),...)

integrate(exp(cos(x)),x)

(15)

Type: Union(Expression(Integer),...)

integrate(sin(x),x)
  integrate(%,x)

   >> Error detected within library code:
   Sorry - cannot handle that integrand yet

integrate(a/h - c*h/12 + (b/h)*r + (c/h)*r^2,r)

(16)

Type: Union(Expression(Integer),...)

integrate(exp(-(a+b*t)^2/2),t)

(17)

Type: Union(Expression(Integer),...)

integrate(exp(-(a+b*t)^2/t),t)

(18)

Type: Union(Expression(Integer),...)

integrate(exp(-1/t),t)

(19)

Type: Union(Expression(Integer),...)

integrate(exp(-1/t),t=1..x)

(20)

Type: Union(pole: potentialPole,...)

Unfortunately, there is currently no easy way to make "assumptions" about variables. Thus, The following won't work:

  \begin{axiom}
   assume(x, real)
   integrate(exp(-1/t),t=1..x)
   \end{axiom}

integrate(t*exp(-(a+b*t)^2/2),t)

(21)

Type: Union(Expression(Integer),...)

integrate(1/(a+z^3), z=0..1,"noPole")

(22)

Type: Union(f1: OrderedCompletion(Expression(Integer)),...)

From the ReduceProblem? (what does axiom do?):

int(1/sqrt(2*PI)*exp(-1/2*log(x)**2),x,0,INFINITY);

   There are 35 exposed and 22 unexposed library operations named *
      having 2 argument(s) but none was determined to be applicable.
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named *
      with argument type(s)
                               PositiveInteger
                                   Domain

      Perhaps you should use "@" to indicate the required return type,
      or "$" to specify which version of the function you need.

integrate(1/sqrt(2*%pi)*exp(-1/2*log(x)**2),x=0..k)

(23)

Type: Union(pole: potentialPole,...)

If you would get a result, you could use limit afterwards, of course.

Mathematical Paradox?

Thu, 10 Feb 2005 17:45:57 -0600 reply