From Numerical Recipes in C, 2nd edition
Section 6.2 Incomplete Gamma Function
http://www.library.cornell.edu/nr/bookcpdf/c6-2.pdf
This Axiom interpreter function implements equation (6.2.7)
fricas
(1) -> Gam(a:Float,x:Float):Float ==
if x<0.0 or a<0.0 then error "Invalid arguments"
if x=0.0 then return Gamma(a)
ITMAX ==> 100 -- Maximum allowed number of iterations
FPMIN ==> 1.0e-1000 -- near the smallest representable number
-- (there is not smallest number for Float!)
EPS := (10.0^(-digits()$Float+1))$Float -- Relative accuracy
an: Float
del: Float
b:Float := x+1.0-a -- Set up for evaluating continued fraction
c:Float := 1.0/FPMIN -- by modified Lentz' method (section 5.2)
d:Float := 1.0/b -- with b_0 = 0
h:Float := d
i := 1
repeat -- Iterate to convergence
an := -i*(i-a)
b := b + 2.0
d := an*d+b
if abs(d) < FPMIN then d := FPMIN
c := b+an/c;
if abs(c) < FPMIN then c := FPMIN
d := 1.0/d;
del := d*c
h := h*del
if i>ITMAX or abs(del-1.0) < EPS then break
i := i + 1
if i>ITMAX then error("a too large, ITMAX too small")
exp(-x)*x^a*h -- Put factors in front
Function declaration Gam : (Float, Float) -> Float has been added to
workspace.
Type: Void
fricas
Gam(0,1)
fricas
Compiling function Gam with type (Float, Float) -> Float
Error signalled from user code in function Gam:
a too large, ITMAX too small
Let's try that again with more precision:
fricas
digits(100)
fricas
Gam(0,1)
Error signalled from user code in function Gam:
a too large, ITMAX too small
Let us do this using machine floating point (DoubleFloat?) in Axiom's
library programming language SPAD
spad
)abbrev package SFX SpecialFunctionsExtended
SpecialFunctionsExtended: Exports == Implementation where
ITMAX ==> 100.0::DoubleFloat -- Maximum allowed number of iterations
-- near the smallest representable number, can not make it smaller because
-- otherwise 1/FPMIN overflows
FPMIN ==> 1.0e-308::DoubleFloat
Exports ==> with
Gamma:(DoubleFloat,DoubleFloat)->DoubleFloat
Implementation ==> add
Gamma(a:DoubleFloat,x:DoubleFloat):DoubleFloat ==
if x<0 or a<0 then error "Invalid arguments"
if x=0 then return Gamma(a)
EPS := (10.0::DoubleFloat^(-digits()$DoubleFloat + 1))$DoubleFloat -- Relative accuracy
b:DoubleFloat := x+1-a -- Set up for evaluating continued fraction
c:DoubleFloat := 1/FPMIN -- by modified Lentz' method (section 5.2)
d:DoubleFloat := 1/b -- with b_0 = 0
h:DoubleFloat := d
i:DoubleFloat := 1
repeat -- Iterate to convergence
an:DoubleFloat := -i*(i-a)
b := b + 2.0::DoubleFloat
d := an*d+b
if abs(d) < FPMIN then d := FPMIN
c := b+an/c;
if abs(c) < FPMIN then c := FPMIN
d := 1/d;
del:DoubleFloat := d*c
h := h*del
if i>ITMAX or abs(del-1) < EPS then break
i := i + 1
if i>ITMAX then error("a too large, ITMAX too small")
return exp(-x+log(x)*a) * h -- Put factors in front
spad
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/52052831343972396-25px004.spad
using old system compiler.
SFX abbreviates package SpecialFunctionsExtended
------------------------------------------------------------------------
initializing NRLIB SFX for SpecialFunctionsExtended
compiling into NRLIB SFX
compiling exported Gamma : (DoubleFloat,DoubleFloat) -> DoubleFloat
Time: 0 SEC.
(time taken in buildFunctor: 0)
Time: 0 SEC.
Warnings:
[1] Gamma: d has no value
[2] Gamma: c has no value
Cumulative Statistics for Constructor SpecialFunctionsExtended
Time: 0.01 seconds
finalizing NRLIB SFX
Processing SpecialFunctionsExtended for Browser database:
--->-->SpecialFunctionsExtended(constructor): Not documented!!!!
--->-->SpecialFunctionsExtended((Gamma ((DoubleFloat) (DoubleFloat) (DoubleFloat)))): Not documented!!!!
--->-->SpecialFunctionsExtended(): Missing Description
; compiling file "/var/aw/var/LatexWiki/SFX.NRLIB/SFX.lsp" (written 01 FEB 2026 09:35:48 AM):
; wrote /var/aw/var/LatexWiki/SFX.NRLIB/SFX.fasl
; compilation finished in 0:00:00.016
------------------------------------------------------------------------
SpecialFunctionsExtended is now explicitly exposed in frame initial
SpecialFunctionsExtended will be automatically loaded when needed
from /var/aw/var/LatexWiki/SFX.NRLIB/SFXApparently in SPAD we must write 0 and 1 instead of 0.0 and 1.0
because 0 and 1 are functions exported by DoubleFloat but 0.0
and 1.0 are by default, constructs of Float. We must also be careful
to declare the type of other constants.
fricas
Gamma(a,x)
Type: Expression(Integer)
fricas
Gamma(0,1)$SFX
fricas
Gamma(0,2)$SFX
fricas
Gamma(1,1)$SFX
fricas
Gamma(1,1.1)$SFX
fricas
Gamma(5,10)$SFX
fricas
Gamma(5,11)$SFX
fricas
Gamma(7,0)$SFX
Note: we need package call because otherwise we get builtin function, either from
Expression(Integer) or (unimplemented) from DoubleFloat?.
Exactly the same code can also be compiled using Aldor (Axiom library
compiler version 2):
aldor
#include "axiom.as";
#pile
SpecialFunctionsExtended2: Exports == Implementation where
ITMAX ==> 100.0::DoubleFloat -- Maximum allowed number of iterations
FPMIN ==> 1.0e-308::DoubleFloat -- near the smallest representable number
Exports ==> with
Gamma:(DoubleFloat,DoubleFloat)->DoubleFloat
Implementation ==> add
Gamma(a:DoubleFloat,x:DoubleFloat):DoubleFloat ==
if x<0 or a<0 then error "Invalid arguments"
if x=0 then return Gamma(a)
EPS := (10.0::DoubleFloat**(-digits()$DoubleFloat))$DoubleFloat -- Relative accuracy
b:DoubleFloat := x+1-a -- Set up for evaluating continued fraction
c:DoubleFloat := 1/FPMIN -- by modified Lentz' method (section 5.2)
d:DoubleFloat := 1/b -- with b_0 = 0
h:DoubleFloat := d
i:DoubleFloat := 1
repeat -- Iterate to convergence
an:DoubleFloat := -i*(i-a)
b := b + 2.0::DoubleFloat
d := an*d+b
if abs(d) < FPMIN then d := FPMIN
c := b+an/c;
if abs(c) < FPMIN then c := FPMIN
d := 1/d;
del:DoubleFloat := d*c
h := h*del
if i>ITMAX or abs(del-1) < EPS then break
i := i + 1
if i>ITMAX then error("a too large, ITMAX too small")
return exp(-x+log(x)*a) * h -- Put factors in front
aldor
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/sfx2.as using
Aldor compiler and options
-O -Fasy -Fao -Flsp -lfricas -Mno-ALDOR_W_WillObsolete -DFriCAS -Y $FRICAS/algebra -I $FRICAS/algebra
Use the system command )set compiler args to change these
options.
"/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/sfx2.as", line 1:
#include "axiom.as";
^
[L1 C1] #1 (Error) Could not open file `axiom.as'.
The )library system command was not called after compilation.fricas
Gamma(a,x)
Type: Expression(Integer)
fricas
Gamma(0,1)
Type: Expression(Integer)
fricas
Gamma(0,2)
Type: Expression(Integer)
fricas
Gamma(1,1)
Type: Expression(Integer)
fricas
Gamma(1,1.1)
fricas
Gamma(5,10)
Type: Expression(Integer)
fricas
Gamma(5,11)
Type: Expression(Integer)
fricas
Gamma(1,0)
Type: Expression(Integer)
fricas
Gamma(7,0)
Type: Expression(Integer)
This is false (result is 720):
Gam(7,0)
0.0
Type: Float
Sorry I forgot the limiting case. Actually the algoritm in Recipes
is a little more sophisticated. It uses the series expansion of
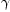
eq. (6.25) for
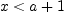
to compute
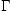
since it converges
more rapidly.
fricas
Gam(7,0)
Type: Float
fricas
Gam(7,0.1)
Type: Float
fricas
Gam(7,0.2)
Type: Float
The command
)set functions compile on is necessary in order to
avoid a seg fault with certain function definitions in the Axiom
interpreter. See:
#196
fricas
)set functions compile on
fricas
j:=120
fricas
nume(a) == cons(1 :: Float,[((a-i)*i) :: Float for i in 1..]);
Type: Void
fricas
dene(a,x) == [(x+2*i+1-a) :: Float for i in 0..];
Type: Void
fricas
cfe(a,x) == continuedFraction(0,nume(a),dene(a,x));
Type: Void
fricas
ccfe(a,x) == convergents cfe(a,x);
Type: Void
fricas
gamcfe(a,x) == exp(-x)*x^a*ccfe(a,x).j;
Type: Void
fricas
gamcfe(2,3)
fricas
Compiling function nume with type PositiveInteger -> Stream(Float)
fricas
Compiling function dene with type (PositiveInteger, PositiveInteger)
-> Stream(Float)
fricas
Compiling function cfe with type (PositiveInteger, PositiveInteger)
-> ContinuedFraction(Float)
fricas
Compiling function ccfe with type (PositiveInteger, PositiveInteger)
-> Stream(Fraction(Float))
There are 31 exposed and 40 unexposed library operations named *
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op *
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named *
with argument type(s)
Expression(Integer)
Fraction(Float)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
FriCAS will attempt to step through and interpret the code.
Type: Expression(Float)
fricas
E1(x)== gamcfe(0,x)
Type: Void
fricas
E1(2.0)
Cannot compile map: gamcfe
We will attempt to interpret the code.
fricas
Compiling function nume with type NonNegativeInteger -> Stream(Float
)fricas
Compiling function dene with type (NonNegativeInteger, Float) ->
Stream(Float)
fricas
Compiling function cfe with type (NonNegativeInteger, Float) ->
ContinuedFraction(Float)
fricas
Compiling function ccfe with type (NonNegativeInteger, Float) ->
Stream(Fraction(Float))
Type: Fraction(Float)
There seems to be a problem with Axiom's ContinuedFraction
? domain.
The type of the result is shown as
Fraction Float but this is
nonesense.
fricas
ff:Fraction Float
Fraction(Float) is not a valid type.
Something similar happens if the argument is Fraction Integer
fricas
nume(a) == cons(1,[((a-i)*i) for i in 1..]);
Compiled code for nume has been cleared.
Compiled code for cfe has been cleared.
Compiled code for ccfe has been cleared.
Compiled code for gamcfe has been cleared.
Compiled code for E1 has been cleared.
1 old definition(s) deleted for function or rule nume
Type: Void
fricas
dene(a,x) == [(x+2*i+1-a) for i in 0..];
Compiled code for dene has been cleared.
1 old definition(s) deleted for function or rule dene
Type: Void
fricas
cfe(a,x) == continuedFraction(0,nume(a),dene(a,x));
1 old definition(s) deleted for function or rule cfe
Type: Void
fricas
ccfe(a,x) == convergents cfe(a,x);
1 old definition(s) deleted for function or rule ccfe
Type: Void
fricas
ccfe(0,2::Float)
fricas
Compiling function nume with type NonNegativeInteger -> Stream(
Integer)fricas
Compiling function dene with type (NonNegativeInteger, Float) ->
Stream(Float)
fricas
Compiling function cfe with type (NonNegativeInteger, Float) ->
ContinuedFraction(Float)
fricas
Compiling function ccfe with type (NonNegativeInteger, Float) ->
Stream(Fraction(Float))
Type: Stream(Fraction(Float))
fricas
ccfe(0,2::Fraction Integer)
fricas
Compiling function dene with type (NonNegativeInteger, Fraction(
Integer)) -> Stream(Fraction(Integer))
fricas
Compiling function cfe with type (NonNegativeInteger, Fraction(
Integer)) -> ContinuedFraction(Fraction(Integer))
fricas
Compiling function ccfe with type (NonNegativeInteger, Fraction(
Integer)) -> Stream(Fraction(Fraction(Integer)))
Type: Stream(Fraction(Fraction(Integer)))
Fraction Fraction Integer is also nonesense.
![\label{eq25}\begin{array}{@{}l}
\displaystyle
\left[{0.0}, \:{0.3333333333 \<u> 3333333333}, \:{0.3571428571 \</u> 4285714286}, \: \right.
\
\
\displaystyle
\left.{0.3604651162 \<u> 7906976744}, \:{0.3611111111 \</u> 111111
1111}, \: \right.
\
\
\displaystyle
\left.{0.3612656467 \<u> 3157162726}, \:{0.3613083856 \</u> 869707
7301}, \: \right.
\
\
\displaystyle
\left.{0.3613215638 \<u> 624830248}, \:{0.3613259896 \</u> 0595485
929}, \: \right.
\
\
\displaystyle
\left.{0.3613275827 \_ 1362214001}, \: \ldots \right]
\label{eq25}\begin{array}{@{}l}
\displaystyle
\left[{0.0}, \:{0.3333333333 \<u> 3333333333}, \:{0.3571428571 \</u> 4285714286}, \: \right.
\
\
\displaystyle
\left.{0.3604651162 \<u> 7906976744}, \:{0.3611111111 \</u> 111111
1111}, \: \right.
\
\
\displaystyle
\left.{0.3612656467 \<u> 3157162726}, \:{0.3613083856 \</u> 869707
7301}, \: \right.
\
\
\displaystyle
\left.{0.3613215638 \<u> 624830248}, \:{0.3613259896 \</u> 0595485
929}, \: \right.
\
\
\displaystyle
\left.{0.3613275827 \_ 1362214001}, \: \ldots \right]](images/6855592695027614069-16.0px.png)
![\label{eq26}\begin{array}{@{}l}
\displaystyle
\left[ 0, \:{\frac{1}{3}}, \:{\frac{5}{14}}, \:{\frac{31}{86}}, \:{\frac{13}{36}}, \:{\frac{1039}{2876}}, \: \right.
\
\
\displaystyle
\left.{\frac{5291}{14644}}, \:{\frac{20221}{55964}}, \:{\frac{1
93003}{534152}}, \: \right.
\
\
\displaystyle
\left.{\frac{385207}{1066088}}, \: \ldots \right]
\label{eq26}\begin{array}{@{}l}
\displaystyle
\left[ 0, \:{\frac{1}{3}}, \:{\frac{5}{14}}, \:{\frac{31}{86}}, \:{\frac{13}{36}}, \:{\frac{1039}{2876}}, \: \right.
\
\
\displaystyle
\left.{\frac{5291}{14644}}, \:{\frac{20221}{55964}}, \:{\frac{1
93003}{534152}}, \: \right.
\
\
\displaystyle
\left.{\frac{385207}{1066088}}, \: \ldots \right]](images/3129639153245245982-16.0px.png)