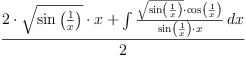IntegrationLet's do some integration examples: fricas (1) -> integrate(%e^x,
Type: Union(Expression(Integer),
fricas integrate(x^2/sqrt(4-x^2),
Type: Union(Expression(Integer),
Below FriCAS gives up because sign of fricas integrate(exp(-a*x^2),
Type: Union(fail: failed,
The following won't "work", see CommonMistakes: fricas integrate(exp(-a::PositiveInteger*x^2), fricas integrate((x^3+x^2+2)/(x*(x^2-1)^2),
Type: Union(Expression(Integer),
fricas integrate(2*x/sin(x)^2,
Type: Union(Expression(Integer),
Comparing FriCAS and Reduce: fricas integrate(sin(1/x),
Type: Union(Expression(Integer),
A different problem, where FriCAS has to give up: fricas integrate(sqrt(sin(1/x)), In Reduce:
fricas integrate(exp(-x^2),
Type: Union(Expression(Integer),
fricas integrate(sin(x)/x,
Type: Union(Expression(Integer),
fricas differentiate(%,
Type: Expression(Integer)
fricas integrate(sin(1/x), fricas integrate(2*x/sin(x)^2,
Type: Union(pole: potentialPole,
fricas integrate(sin(x),
Type: Union(f1: OrderedCompletion?(Expression(Integer)),
fricas integrate(atan(x/a)/x,
Type: Union(Expression(Integer),
fricas integrate(1/(a+z^3),
Type: Union(f1: OrderedCompletion?(Expression(Integer)),
fricas integrate(x^3+x^2/4+x,
Type: Polynomial(Fraction(Integer))
You cannot integrate Expression Float fricas integrate(50*%e^(-0.02*t), But symbolic integration works with integer expressions fricas integrate(50*%e^(-0.02*t)::Expression Fraction Integer,
Type: Union(Expression(Fraction(Integer)),
fricas integrate(exp(cos(x)),
Type: Union(Expression(Integer),
fricas integrate(sin(x),
Type: Union(Expression(Integer),
fricas integrate(%,
Type: Union(Expression(Integer),
fricas integrate(a/h - c*h/12 + (b/h)*r + (c/h)*r^2,
Type: Union(Expression(Integer),
fricas integrate(exp(-(a+b*t)^2/2),
Type: Union(Expression(Integer),
fricas integrate(exp(-(a+b*t)^2/t),
Type: Union(Expression(Integer),
fricas integrate(exp(-1/t),
Type: Union(Expression(Integer),
fricas integrate(exp(-1/t),
Type: Union(pole: potentialPole,
Unfortunately, there is currently no easy way to make "assumptions" about variables. Thus, The following won't work:
\begin{axiom}
assume(x, real)
integrate(exp(-1/t),t=1..x)
\end{axiom}
fricas integrate(t*exp(-(a+b*t)^2/2),
Type: Union(Expression(Integer),
fricas integrate(1/(a+z^3),
Type: Union(f1: OrderedCompletion?(Expression(Integer)),
From the ReduceProblem?: fricas integrate(1/sqrt(2*%pi)*exp(-1/2*log(x)^2),
Type: Union(f1: OrderedCompletion?(Expression(Integer)),
fricas integrate(1/sqrt(2*%pi)*exp(-1/2*log(x)^2),
Type: Union(Expression(Integer),
If you would get a result, you could use limit afterwards, of course.
Curve has an infinite area...but a finite volume (I think I did this correctly)! fricas integrate(1/x,
Type: Union(Expression(Integer),
fricas integrate(sqrt(x),
Type: Union(Expression(Integer),
fricas integrate(sqrt(x^3+x),
Type: Union(Expression(Integer),
fricas )set output tex off fricas )set output algebra on Type: Union(Expression(Integer),
fricas integrate(( a*cos( m + n*t + o*t*t/2 ) )- ( b*sin( m + n*t + o*t*t/2 ) ), Type: Union(Expression(Integer),
fricas )set output algebra off fricas )set output tex on fricas integrate(-2*(3-3*t)^2*(3*t),
Type: Polynomial(Fraction(Integer))
fricas integrate(1/(1+x^2),
Type: Union(pole: potentialPole,
fricas integrate(1/(1+x^2),
Type: Union(f1: OrderedCompletion?(Expression(Integer)),
fricas integrate(x^6*exp(-x^2),
Type: Union(f1: OrderedCompletion?(Expression(Integer)),
fricas integrate(1/sqrt(1/x+1),
Type: Union(Expression(Integer),
fricas integrate(sin(sin x),
Type: Union(Expression(Integer),
fricas integrate(a/2*(1-cos(b*t)),
Type: Union(Expression(Integer),
yet another test that shall work but not in maple ? --unknown, Thu, 09 Mar 2006 09:21:47 -0600 reply fricas integrate(tan(atan(x)/3),
Type: Union(Expression(Integer),
fricas integrate(x,
Type: Polynomial(Fraction(Integer))
fricas simplify((1/(2*z))*z^2)
Type: Expression(Integer)
fricas integrate((1/(2*z))*z^2,
Type: Union(Expression(Integer),
fricas integrate(log(x),
Type: Union(Expression(Integer),
fricas integrate(1/x,
Type: Union(Expression(Integer),
fricas integrate(0^0,
Type: Polynomial(Fraction(Integer))
fricas integrate( log(y)^3/(y*(y-1)),
Type: Union(Expression(Integer),
fricas integrate(exp(-x^2),
Type: Union(f1: OrderedCompletion?(Expression(Integer)),
fricas integrate(x^2*exp(-x^2),
Type: Union(f1: OrderedCompletion?(Expression(Integer)),
No ; after command or else output is supressed.
fricas integrate(exp(%i*2*%pi*f*t),
Type: Union(f1: OrderedCompletion?(Expression(Complex(Integer))),
FriCAS and Maxima not capable of this integrand --WinnieThePooh?, Tue, 29 May 2007 17:24:44 -0500 reply
fricas integrate(exp(sin(x)),
Type: Union(Expression(Integer),
fricas integrate(sqrt(x+sqrt(1+x^2))/x,
Type: Union(Expression(Integer),
fricas )set output algebra on
Type: Union(Expression(Integer),
fricas unparse(r2::InputForm)
Type: String
Test fricas ii := integral(sin(x),
Type: Expression(Integer)
fricas integrate((7*x^13+10*x^8+4*x^7-7*x^6-4*x^3-4*x^2+3*x+3)/(x^14-2*x^8-2*x^7-2*x^4-4*x^3-x^2+2*x+1),
Type: Union(Expression(Integer),
|
|
|
|
last edited 2 years ago by test1 |