help links subscribe changes refresh edit

	SandBox
SandBox Gamma ←	↑	→ SandBox LaTeX

SandBox Integration

Edit detail for SandBox Integration revision 1 of 19

	1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
Editor: Time: 2007/11/18 18:05:04 GMT-8
Note: Axiom and Maxima not capable of this integrand

changed:
-
Integration

  Let's do some integration examples:

\begin{axiom}
integrate(%e**x, x)
\end{axiom}

\begin{reduce}
load_package SPECFN;
\end{reduce}

\begin{reduce}
on ROUNDED,ADJPREC;
\end{reduce}

\begin{reduce}
Ei(1.00000000000000000001);
Ei(1.0);
Ei(2.0);
\end{reduce}

Can Reduce compute Ei in arbitrary precision?

See http://www.uni-koeln.de/REDUCE/3.6/doc/specfn/

Also http://homepages.inf.ed.ac.uk/mtoussai/publications/toussaint-99-mexico.pdf

Reset
\begin{reduce}
off ROUNDED,ADJPREC;
\end{reduce}

\begin{reduce}
int(cos(x),x,0,pi);
\end{reduce}

\begin{axiom}
integrate(x^2/sqrt(4-x^2),x)
\end{axiom}

\begin{axiom}
integrate(exp(-a*x**2),x=0..%plusInfinity)
\end{axiom}

The following won't "work", see CommonMistakes:

\begin{axiom}
integrate(exp(-a::PositiveInteger*x**2),x=0..%plusInfinity)
\end{axiom}

\begin{axiom}
integrate((x^3+x^2+2)/(x*(x^2-1)^2), x)
\end{axiom}

\begin{axiom}
integrate(2*x/sin(x)^2,x)
\end{axiom}

Comparing Axiom and Reduce:

\begin{axiom}
integrate(sin(1/x),x)
\end{axiom}

\begin{reduce}
int(sin(1/x),x);
\end{reduce}

Hell, why does the following blow MathAction?::

  !\begin{reduce}
  load_package algint;
  int(sin(1/x),x);
  \end{reduce}

A different problem, where Axiom has to give up:

\begin{axiom}
integrate(sqrt(sin(1/x)),x)
\end{axiom}

However, in Reduce:
Again, why does the following blow MathAction?::
  
  !\begin{reduce}
  load_package algint;
  int(sqrt(sin(1/x)),x);
  \end{reduce}

\begin{axiom}
integrate(exp(-x^2),x)
\end{axiom}

\begin{axiom}
integrate(sin(x)/x,x)
differentiate(%,x)
\end{axiom}

\begin{axiom}
integrate(sin(1/x),x=%minusInfinity..%plusInfinity,"noPole")
\end{axiom}

\begin{axiom}
integrate(2*x/sin(x)^2,x=1/2..1);
\end{axiom}

\begin{axiom}
integrate(sin(x),x=0..%pi/2)
\end{axiom}

\begin{axiom}
integrate(atan(x/a)/x,x)
\end{axiom}

\begin{axiom}
integrate(1/(a+z^3), z=0..1,"noPole")
\end{axiom}

\begin{axiom}
integrate(x^3+x^2/4+x,x)
\end{axiom}

You cannot integrate Expression Float
\begin{axiom}
integrate(50*%e^(-0.02*t),t)
\end{axiom}

But symbolic integration works with integer expressions
\begin{axiom}
  integrate(50*%e^(-0.02*t)::Expression Fraction Integer,t)
\end{axiom}

\begin{axiom}
  integrate(exp(cos(x)),x)
\end{axiom}

\begin{axiom}
  integrate(sin(x),x)
  integrate(%,x)
\end{axiom}

\begin{axiom}
  integrate(a/h - c*h/12 + (b/h)*r + (c/h)*r^2,r)
\end{axiom}

\begin{axiom}
  integrate(exp(-(a+b*t)^2/2),t)
\end{axiom}

\begin{axiom}
  integrate(exp(-(a+b*t)^2/t),t)
\end{axiom}

\begin{axiom}
  integrate(exp(-1/t),t)
\end{axiom}

\begin{axiom}
  integrate(exp(-1/t),t=1..x)
\end{axiom}

Unfortunately, there is currently no easy way to make "assumptions" about
variables. Thus, The following won't work::

  !\begin{axiom}
   assume(x, real)
   integrate(exp(-1/t),t=1..x)
   \end{axiom}


\begin{axiom}
integrate(t*exp(-(a+b*t)^2/2),t)
\end{axiom}

\begin{axiom}
integrate(1/(a+z^3), z=0..1,"noPole")
\end{axiom}

From the ReduceProblem (what does axiom do?):

\begin{axiom}
int(1/sqrt(2*PI)*exp(-1/2*log(x)**2),x,0,INFINITY);
\end{axiom}

From MartinRubey Thu Oct 7 10:18:13 -0500 2004
From: Martin Rubey
Date: Thu, 07 Oct 2004 10:18:13 -0500
Subject: 
Message-ID: <16741.31098.837887.890502@gargle.gargle.HOWL>
In-Reply-To: <20041007093033-0500@page.axiom-developer.org>

Well, you should use Axiom syntax. Note that 'PI' is a domain, spelled out:
'PositiveInteger' in Axiom, the constant $\pi$ is denoted '%pi'. Furthermore,
the operation you want is called 'integrate'. Finally, infinity is denoted
'%infinity', but in fact, I wouldn't know how to do such integrals in Axiom
anyway. Thus, the best I get is:

\begin{axiom}
 integrate(1/sqrt(2*%pi)*exp(-1/2*log(x)**2),x=0..k)
\end{axiom}

If you would get a result, you could use limit afterwards, of course.

From unknown Thu Feb 10 17:45:57 -0600 2005
From: 
Date: Thu, 10 Feb 2005 17:45:57 -0600
Subject: Mathematical Paradox?
Message-ID: <20050210174557-0600@page.axiom-developer.org>

Area under the curve:
\begin{axiom}
integrate(1/x,x=1..%plusInfinity)
\end{axiom}

From unknown Thu Feb 10 17:47:59 -0600 2005
From: 
Date: Thu, 10 Feb 2005 17:47:59 -0600
Subject: Paradox Part2:
Message-ID: <20050210174759-0600@page.axiom-developer.org>

Volume under that curve:
\begin{axiom}
integrate(%pi*((1/x)^2), x=1..%plusInfinity)
\end{axiom}

Curve has an infinite area...but a finite volume (I think I did this correctly)!

From unknown Tue May 17 18:52:42 -0500 2005
From: unknown
Date: Tue, 17 May 2005 18:52:42 -0500
Subject: 
Message-ID: <20050517185242-0500@page.axiom-developer.org>

\begin{axiom}
  integrate(1/x,x)
\end{axiom}

From unknown Tue May 17 18:53:28 -0500 2005
From: unknown
Date: Tue, 17 May 2005 18:53:28 -0500
Subject: 
Message-ID: <20050517185328-0500@page.axiom-developer.org>

\begin{axiom}
integrate(sqrt(x),x)
\end{axiom}

From unknown Tue May 17 18:54:19 -0500 2005
From: unknown
Date: Tue, 17 May 2005 18:54:19 -0500
Subject: 
Message-ID: <20050517185419-0500@page.axiom-developer.org>

\begin{axiom}
integrate(sqrt(x^3+x),x)
\end{axiom}


From unknown Sun Jun 19 20:16:03 -0500 2005
From: unknown
Date: Sun, 19 Jun 2005 20:16:03 -0500
Subject: a turning moving body
Message-ID: <20050619201603-0500@page.axiom-developer.org>

\begin{axiom}
integrate(( a*sin( m + n*t + o*t*t/2 ) )/( n + ot ) + ( b*cos( m + n*t + o*t*t/2 ) )/( n + ot ), t)
\end{axiom}

From unknown Sun Jun 19 23:16:48 -0500 2005
From: unknown
Date: Sun, 19 Jun 2005 23:16:48 -0500
Subject: a turning accelerating body
Message-ID: <20050619231648-0500@page.axiom-developer.org>

\begin{axiom}
integrate(( a*cos( m + n*t + o*t*t/2 ) )- ( b*sin( m + n*t + o*t*t/2 ) ), t)
\end{axiom}

From unknown Sun Jun 26 16:02:47 -0500 2005
From: unknown
Date: Sun, 26 Jun 2005 16:02:47 -0500
Subject: 
Message-ID: <20050626160247-0500@page.axiom-developer.org>

\begin{axiom}
integrate(-2*(3-3*t)^2*(3*t),t)
\end{axiom}


From unknown Sun Oct 30 09:27:40 -0600 2005
From: unknown
Date: Sun, 30 Oct 2005 09:27:40 -0600
Subject: 
Message-ID: <20051030092740-0600@page.axiom-developer.org>

integrate(1/(1+x**2),x=-u..u)

From unknown Sun Oct 30 09:29:01 -0600 2005
From: unknown
Date: Sun, 30 Oct 2005 09:29:01 -0600
Subject: 
Message-ID: <20051030092901-0600@page.axiom-developer.org>

\begin{axiom}
integrate(1/(1+x**2),x=-u..u)
\end{axiom}

From unknown Tue Nov 1 10:35:26 -0600 2005
From: unknown
Date: Tue, 01 Nov 2005 10:35:26 -0600
Subject: 
Message-ID: <20051101103526-0600@www.axiom-developer.org>

\begin{axiom}
  integrate(x**6*exp(-x**2), x=0..%plusInfinity)
\end{axiom}



From unknown Wed Nov 2 16:59:21 -0600 2005
From: unknown
Date: Wed, 02 Nov 2005 16:59:21 -0600
Subject: 
Message-ID: <20051102165921-0600@www.axiom-developer.org>

integrate(1/sqrt(1/x+1),x)

From unknown Wed Nov 2 17:00:21 -0600 2005
From: unknown
Date: Wed, 02 Nov 2005 17:00:21 -0600
Subject: 
Message-ID: <20051102170021-0600@www.axiom-developer.org>

\begin{axiom}
integrate(1/sqrt(1/x+1),x)
\end{axiom}

From unknown Wed Nov 23 08:30:18 -0600 2005
From: unknown
Date: Wed, 23 Nov 2005 08:30:18 -0600
Subject: 
Message-ID: <20051123083018-0600@www.axiom-developer.org>

integrate(sin(sin x), x)

From unknown Fri Nov 25 16:28:37 -0600 2005
From: unknown
Date: Fri, 25 Nov 2005 16:28:37 -0600
Subject: 
Message-ID: <20051125162837-0600@www.axiom-developer.org>

integrate(a/2*(1-cos(b*t)),t)

From unknown Thu Mar 9 09:21:47 -0600 2006
From: unknown
Date: Thu, 09 Mar 2006 09:21:47 -0600
Subject: yet another test that shall work but not in maple ?
Message-ID: <20060309092147-0600@wiki.axiom-developer.org>

integrate(tan(arctan(x)/3),x)

From unknown Thu Mar 9 09:22:56 -0600 2006
From: unknown
Date: Thu, 09 Mar 2006 09:22:56 -0600
Subject: 
Message-ID: <20060309092256-0600@wiki.axiom-developer.org>
In-Reply-To: <20060309092147-0600@wiki.axiom-developer.org>

integrate(tan(arctan(x)/3),x);

From unknown Sat Mar 11 12:40:39 -0600 2006
From: unknown
Date: Sat, 11 Mar 2006 12:40:39 -0600
Subject: 
Message-ID: <20060311124039-0600@wiki.axiom-developer.org>

integrate(x, x)

From unknown Sat Mar 11 12:41:33 -0600 2006
From: unknown
Date: Sat, 11 Mar 2006 12:41:33 -0600
Subject: 
Message-ID: <20060311124133-0600@wiki.axiom-developer.org>

\begin{axiom}
integrate(x, x)
\end{axiom}


From unknown Sat Mar 11 12:43:17 -0600 2006
From: unknown
Date: Sat, 11 Mar 2006 12:43:17 -0600
Subject: 
Message-ID: <20060311124317-0600@wiki.axiom-developer.org>

\begin{axiom}
integrate((1/(2*z))*z^2), z)
\end{axiom}


From unknown Sat Mar 11 12:44:05 -0600 2006
From: unknown
Date: Sat, 11 Mar 2006 12:44:05 -0600
Subject: 
Message-ID: <20060311124405-0600@wiki.axiom-developer.org>

\begin{axiom}
integrate((1/(2*z))*z^2, z)
\end{axiom}


From unknown Sat Mar 11 12:47:35 -0600 2006
From: unknown
Date: Sat, 11 Mar 2006 12:47:35 -0600
Subject: 
Message-ID: <20060311124735-0600@wiki.axiom-developer.org>

\begin{axiom}
simplify((1/(2*z))*z^2)
integrate((1/(2*z))*z^2, z)
\end{axiom}


From unknown Sat May 6 09:17:11 -0500 2006
From: unknown
Date: Sat, 06 May 2006 09:17:11 -0500
Subject: 
Message-ID: <20060506091711-0500@wiki.axiom-developer.org>

integrate(ln(x),x)

From unknown Sat May 6 09:20:14 -0500 2006
From: unknown
Date: Sat, 06 May 2006 09:20:14 -0500
Subject: 
Message-ID: <20060506092014-0500@wiki.axiom-developer.org>

integrate(1/x,x)

From unknown Sat May 6 16:50:37 -0500 2006
From: unknown
Date: Sat, 06 May 2006 16:50:37 -0500
Subject: 
Message-ID: <20060506165037-0500@wiki.axiom-developer.org>

\begin{axiom}
integrate(0**0,x)
\end{axiom}

From unknown Tue May 9 09:56:50 -0500 2006
From: unknown
Date: Tue, 09 May 2006 09:56:50 -0500
Subject: from fr.sci.maths
Message-ID: <20060509095650-0500@wiki.axiom-developer.org>

\begin{axiom}
integrate( ln(y)^3/(y*(y-1)),y)
\end{axiom}


From unknown Tue May 9 09:58:11 -0500 2006
From: unknown
Date: Tue, 09 May 2006 09:58:11 -0500
Subject: from fr.sci.maths
Message-ID: <20060509095811-0500@wiki.axiom-developer.org>

\begin{axiom}
integrate( log(y)^3/(y*(y-1)),y)
\end{axiom}


From unknown Mon May 29 14:20:28 -0500 2006
From: unknown
Date: Mon, 29 May 2006 14:20:28 -0500
Subject: 
Message-ID: <20060529142028-0500@wiki.axiom-developer.org>

\begin{axiom}
integrate(exp(-x^2),x=0..%plusInfinity)
\end{axiom}


From unknown Mon May 29 14:21:39 -0500 2006
From: unknown
Date: Mon, 29 May 2006 14:21:39 -0500
Subject: 
Message-ID: <20060529142139-0500@wiki.axiom-developer.org>

integrate(x**2*exp(-x^2),x=0..%plusInfinity)

From unknown Wed Jul 19 11:59:36 -0500 2006
From: unknown
Date: Wed, 19 Jul 2006 11:59:36 -0500
Subject: test
Message-ID: <20060719115936-0500@wiki.axiom-developer.org>

No ; after command or else output is supressed.
\begin{axiom}
integrate(exp(%i*2*%pi*f*t), t=0..T)
\end{axiom}


From WinnieThePooh Tue May 29 17:24:44 -0500 2007
From: WinnieThePooh
Date: Tue, 29 May 2007 17:24:44 -0500
Subject: Axiom and Maxima not capable of this integrand
Message-ID: <20070529172444-0500@wiki.axiom-developer.org>

\begin{reduce}
int(exp(sin(x)),x)
\end{reduce}

Integration

Let's do some integration examples:

axiom

integrate(%e**x, x)

$\label{eq1}e^x$

(1)

Type: Union(Expression(Integer),...)

load_package SPECFN;

reduce

on ROUNDED,ADJPREC;

reduce

Ei(1.00000000000000000001);
*** precision increased to 21

reduce

$\displaylines{\qdd euler<em>constant +1.31790215145440389489 \cr}$

Ei(1.0);

reduce

$\displaylines{\qdd euler<em>constant +1.31790215145440389486 \cr}$

Ei(2.0);

reduce

$\displaylines{\qdd euler<em>constant +4.37701869110035730277 \cr}$

Can Reduce compute Ei in arbitrary precision?

See http://www.uni-koeln.de/REDUCE/3.6/doc/specfn/

Also http://homepages.inf.ed.ac.uk/mtoussai/publications/toussaint-99-mexico.pdf

Reset

off ROUNDED,ADJPREC;

reduce

int(cos(x),x,0,pi);

*** ci already defined as operator 

*** si already defined as operator

reduce

$\displaylines{\qdd 0 \cr}$

axiom

integrate(x^2/sqrt(4-x^2),x)

$\label{eq2}{\left( \begin{array}{@{}l} \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle -{{32}\ {\sqrt{-{x^2}+ 4}}}- \ \ \displaystyle {8 \ {x^2}}+{64}$

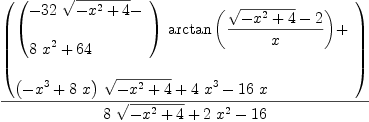(2)

Type: Union(Expression(Integer),...)

axiom

integrate(exp(-a*x**2),x=0..%plusInfinity)

$\label{eq3}\mbox{\tt "failed"}$

(3)

Type: Union(fail: failed,...)

The following won't "work", see CommonMistakes?:

axiom

integrate(exp(-a::PositiveInteger*x**2),x=0..%plusInfinity)

   Cannot convert from type Variable(a) to PositiveInteger for value
   a

axiom

integrate((x^3+x^2+2)/(x*(x^2-1)^2), x)

$\label{eq4}{\left( \begin{array}{@{}l} \displaystyle {{\left(-{5 \ {x^2}}+ 5 \right)}\ {\log \left({x + 1}\right)}}+{{\left({8 \ {x^2}}- 8 \right)}\ {\log \left({x}\right)}}+ \ \ \displaystyle {{\left(-{3 \ {x^2}}+ 3 \right)}\ {\log \left({x - 1}\right)}}-{2 \ x}- 6$

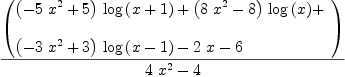(4)

Type: Union(Expression(Integer),...)

axiom

integrate(2*x/sin(x)^2,x)

$\label{eq5}{\left( \begin{array}{@{}l} \displaystyle {2 \ {\sin \left({x}\right)}\ {\log \left({{\sin \left({x}\right)}\over{{\cos \left({x}\right)}+ 1}}\right)}}-{2 \ {\sin \left({x}\right)}\ {\log \left({2 \over{{\cos \left({x}\right)}+ 1}}\right)}}- \ \ \displaystyle {2 \ x \ {\cos \left({x}\right)}}$

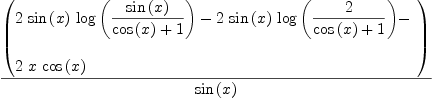(5)

Type: Union(Expression(Integer),...)

Comparing Axiom and Reduce:

axiom

integrate(sin(1/x),x)

$\label{eq6}\int^{ \displaystyle x}{{\sin \left({1 \over \%I}\right)}\ {d \%I}}$

(6)

Type: Union(Expression(Integer),...)

int(sin(1/x),x);

reduce

$\displaylines{\qdd \int {\sin \(\frac{1}{ x}$

Hell, why does the following blow MathAction??:

  \begin{reduce}
  load_package algint;
  int(sin(1/x),x);
  \end{reduce}

A different problem, where Axiom has to give up:

axiom

integrate(sqrt(sin(1/x)),x)

   >> Error detected within library code:
   integrate: implementation incomplete (constant residues)

However, in Reduce: Again, why does the following blow MathAction??:

  \begin{reduce}
  load_package algint;
  int(sqrt(sin(1/x)),x);
  \end{reduce}

axiom

integrate(exp(-x^2),x)

$\label{eq7}{{\erf \left({x}\right)}\ {\sqrt{\pi}}}\over 2$

(7)

Type: Union(Expression(Integer),...)

axiom

integrate(sin(x)/x,x)

$\label{eq8}Si \left({x}\right)$

(8)

Type: Union(Expression(Integer),...)

axiom

differentiate(%,x)

$\label{eq9}{\sin \left({x}\right)}\over x$

(9)

Type: Expression(Integer)

axiom

integrate(sin(1/x),x=%minusInfinity..%plusInfinity,"noPole")

   >> Error detected within library code:
   integrate: pole in path of integration

axiom

integrate(2*x/sin(x)^2,x=1/2..1);

Type: Union(pole: potentialPole,...)

axiom

integrate(sin(x),x=0..%pi/2)

$\label{eq10}1$

(10)

Type: Union(f1: OrderedCompletion(Expression(Integer)),...)

axiom

integrate(atan(x/a)/x,x)

$\label{eq11}\int^{ \displaystyle x}{{{\arctan \left({\%I \over a}\right)}\over \%I}\ {d \%I}}$

(11)

Type: Union(Expression(Integer),...)

axiom

integrate(1/(a+z^3), z=0..1,"noPole")

$\label{eq12}{\left( \begin{array}{@{}l} \displaystyle -{{\sqrt{3}}\ {\log{\left({{3 \ {a^2}\ {{\root{3}\of{a^2}}^2}}+{{\left(-{2 \ {a^3}}+{a^2}\right)}\ {\root{3}\of{a^2}}}+{a^4}-{2 \ {a^3}}}\right)}}}+{2 \ {\sqrt{3}}\ {\log \left({{{\root{3}\of{a^2}}^2}+{2 \ a \ {\root{3}\of{a^2}}}+{a^2}}\right)}}+ \ \ \displaystyle {{12}\ {\arctan \left({{{2 \ {\sqrt{3}}\ {\root{3}\of{a^2}}}-{a \ {\sqrt{3}}}}\over{3 \ a}}\right)}}+{2 \ \pi}$

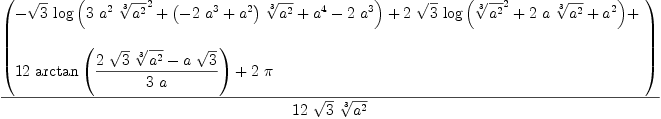(12)

Type: Union(f1: OrderedCompletion(Expression(Integer)),...)

axiom

integrate(x^3+x^2/4+x,x)

$\label{eq13}{{1 \over 4}\ {x^4}}+{{1 \over{12}}\ {x^3}}+{{1 \over 2}\ {x^2}}$

(13)

Type: Polynomial(Fraction(Integer))

You cannot integrate Expression Float

axiom

integrate(50*%e^(-0.02*t),t)

   There are 11 exposed and 8 unexposed library operations named
      integrate having 2 argument(s) but none was determined to be
      applicable. Use HyperDoc Browse, or issue
                            )display op integrate
      to learn more about the available operations. Perhaps
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named
      integrate with argument type(s)
                              Expression(Float)
                                 Variable(t)

      Perhaps you should use "@" to indicate the required return type,
      or "$" to specify which version of the function you need.

But symbolic integration works with integer expressions

axiom

integrate(50*%e^(-0.02*t)::Expression Fraction Integer,t)

$\label{eq14}-{{2500}\ {e^{\left(-{{1 \over{50}}\ t}\right)}}}$

(14)

Type: Union(Expression(Fraction(Integer)),...)

axiom

integrate(exp(cos(x)),x)

$\label{eq15}\int^{ \displaystyle x}{{e^{\cos \left({\%I}\right)}}\ {d \%I}}$

(15)

Type: Union(Expression(Integer),...)

axiom

integrate(sin(x),x)
  integrate(%,x)

   >> Error detected within library code:
   Sorry - cannot handle that integrand yet

axiom

integrate(a/h - c*h/12 + (b/h)*r + (c/h)*r^2,r)

$\label{eq16}{{4 \ c \ {r^3}}+{6 \ b \ {r^2}}+{{\left(-{c \ {h^2}}+{{12}\ a}\right)}\ r}}\over{{12}\ h}$

(16)

Type: Union(Expression(Integer),...)

axiom

integrate(exp(-(a+b*t)^2/2),t)

$\label{eq17}{{\erf \left({{{b \ t}+ a}\over{\sqrt{2}}}\right)}\ {\sqrt{\pi}}}\over{b \ {\sqrt{2}}}$

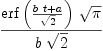(17)

Type: Union(Expression(Integer),...)

axiom

integrate(exp(-(a+b*t)^2/t),t)

$\label{eq18}\int^{ \displaystyle t}{{e^{{-{{\%I^2}\ {b^2}}-{2 \ \%I \ a \ b}-{a^2}}\over \%I}}\ {d \%I}}$

(18)

Type: Union(Expression(Integer),...)

axiom

integrate(exp(-1/t),t)

$\label{eq19}\int^{ \displaystyle t}{{e^{\left(-{1 \over \%I}\right)}}\ {d \%I}}$

(19)

Type: Union(Expression(Integer),...)

axiom

integrate(exp(-1/t),t=1..x)

$\label{eq20}potentialPole$

(20)

Type: Union(pole: potentialPole,...)

Unfortunately, there is currently no easy way to make "assumptions" about variables. Thus, The following won't work:

  \begin{axiom}
   assume(x, real)
   integrate(exp(-1/t),t=1..x)
   \end{axiom}

axiom

integrate(t*exp(-(a+b*t)^2/2),t)

$\label{eq21}{-{a \ {\erf \left({{{b \ t}+ a}\over{\sqrt{2}}}\right)}\ {\sqrt{\pi}}}-{{\sqrt{2}}\ {e^{{-{{b^2}\ {t^2}}-{2 \ a \ b \ t}-{a^2}}\over 2}}}}\over{{b^2}\ {\sqrt{2}}}$

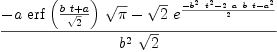(21)

Type: Union(Expression(Integer),...)

axiom

integrate(1/(a+z^3), z=0..1,"noPole")

$\label{eq22}{\left( \begin{array}{@{}l} \displaystyle -{{\sqrt{3}}\ {\log{\left({{3 \ {a^2}\ {{\root{3}\of{a^2}}^2}}+{{\left(-{2 \ {a^3}}+{a^2}\right)}\ {\root{3}\of{a^2}}}+{a^4}-{2 \ {a^3}}}\right)}}}+{2 \ {\sqrt{3}}\ {\log \left({{{\root{3}\of{a^2}}^2}+{2 \ a \ {\root{3}\of{a^2}}}+{a^2}}\right)}}+ \ \ \displaystyle {{12}\ {\arctan \left({{{2 \ {\sqrt{3}}\ {\root{3}\of{a^2}}}-{a \ {\sqrt{3}}}}\over{3 \ a}}\right)}}+{2 \ \pi}$

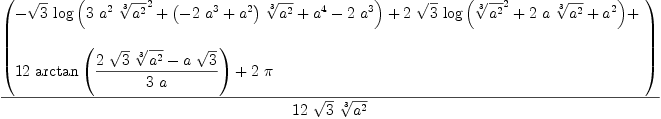(22)

Type: Union(f1: OrderedCompletion(Expression(Integer)),...)

From the ReduceProblem? (what does axiom do?):

axiom

int(1/sqrt(2*PI)*exp(-1/2*log(x)**2),x,0,INFINITY);

   There are 35 exposed and 22 unexposed library operations named *
      having 2 argument(s) but none was determined to be applicable.
      Use HyperDoc Browse, or issue
                                )display op *
      to learn more about the available operations. Perhaps
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named *
      with argument type(s)
                               PositiveInteger
                                   Domain

      Perhaps you should use "@" to indicate the required return type,
      or "$" to specify which version of the function you need.

... --Martin Rubey, Thu, 07 Oct 2004 10:18:13 -0500 reply

Well, you should use Axiom syntax. Note that PI is a domain, spelled out: PositiveInteger in Axiom, the constant $\pi$ is denoted %pi. Furthermore, the operation you want is called integrate. Finally, infinity is denoted %infinity, but in fact, I wouldn't know how to do such integrals in Axiom anyway. Thus, the best I get is:

axiom

integrate(1/sqrt(2*%pi)*exp(-1/2*log(x)**2),x=0..k)

$\label{eq23}potentialPole$

(23)

Type: Union(pole: potentialPole,...)

If you would get a result, you could use limit afterwards, of course.

Mathematical Paradox?: Thu, 10 Feb 2005 17:45:57 -0600 reply

Area under the curve:

axiom

integrate(1/x,x=1..%plusInfinity)

$\label{eq24}+ \infty$

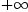
(24)

Type: Union(f1: OrderedCompletion(Expression(Integer)),...)

Paradox Part2:

Thu, 10 Feb 2005 17:47:59 -0600 reply

Volume under that curve:

axiom

integrate(%pi*((1/x)^2), x=1..%plusInfinity)

$\label{eq25}\pi$

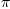
(25)

Type: Union(f1: OrderedCompletion(Expression(Integer)),...)

Curve has an infinite area...but a finite volume (I think I did this correctly)!

... --unknown, Tue, 17 May 2005 18:52:42 -0500 reply

axiom

integrate(1/x,x)

$\label{eq26}\log \left({x}\right)$

(26)

Type: Union(Expression(Integer),...)

... --unknown, Tue, 17 May 2005 18:53:28 -0500 reply

axiom

integrate(sqrt(x),x)

$\label{eq27}{2 \ x \ {\sqrt{x}}}\over 3$

(27)

Type: Union(Expression(Integer),...)

... --unknown, Tue, 17 May 2005 18:54:19 -0500 reply

axiom

integrate(sqrt(x^3+x),x)

$\label{eq28}\int^{ \displaystyle x}{{\sqrt{{\%I^3}+ \%I}}\ {d \%I}}$

(28)

Type: Union(Expression(Integer),...)

a turning moving body --unknown, Sun, 19 Jun 2005 20:16:03 -0500 reply

axiom

integrate(( a*sin( m + n*t + o*t*t/2 ) )/( n + ot ) + ( b*cos( m + n*t
+ o*t*t/2 ) )/( n + ot ), t)

$\label{eq29}\int^{ \displaystyle t}{{{{a \ {\sin \left({{{{\%I^2}\ o}+{2 \ \%I \ n}+{2 \ m}}\over 2}\right)}}+{b \ {\cos \left({{{{\%I^2}\ o}+{2 \ \%I \ n}+{2 \ m}}\over 2}\right)}}}\over{ot + n}}\ {d \%I}}$

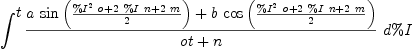(29)

Type: Union(Expression(Integer),...)

a turning accelerating body --unknown, Sun, 19 Jun 2005 23:16:48 -0500 reply

axiom

integrate(( a*cos( m + n*t + o*t*t/2 ) )- ( b*sin( m + n*t +
o*t*t/2 ) ), t)

$\label{eq30}\int^{ \displaystyle t}{{\left(-{b \ {\sin \left({{{{\%I^2}\ o}+{2 \ \%I \ n}+{2 \ m}}\over 2}\right)}}+{a \ {\cos \left({{{{\%I^2}\ o}+{2 \ \%I \ n}+{2 \ m}}\over 2}\right)}}\right)}\ {d \%I}}$

(30)

Type: Union(Expression(Integer),...)

... --unknown, Sun, 26 Jun 2005 16:02:47 -0500 reply

axiom

integrate(-2*(3-3*t)^2*(3*t),t)

$\label{eq31}-{{{27}\over 2}\ {t^4}}+{{36}\ {t^3}}-{{27}\ {t^2}}$

(31)

Type: Polynomial(Fraction(Integer))

... --unknown, Sun, 30 Oct 2005 09:27:40 -0600 reply

integrate(1/(1+x**2),x=-u..u)

... --unknown, Sun, 30 Oct 2005 09:29:01 -0600 reply

axiom

integrate(1/(1+x**2),x=-u..u)

$\label{eq32}potentialPole$

(32)

Type: Union(pole: potentialPole,...)

... --unknown, Tue, 01 Nov 2005 10:35:26 -0600 reply

axiom

integrate(x**6*exp(-x**2), x=0..%plusInfinity)

$\label{eq33}{\Gamma \left({7 \over 2}\right)}\over 2$

(33)

Type: Union(f1: OrderedCompletion(Expression(Integer)),...)

... --unknown, Wed, 02 Nov 2005 16:59:21 -0600 reply

integrate(1/sqrt(1/x+1),x)

... --unknown, Wed, 02 Nov 2005 17:00:21 -0600 reply

axiom

integrate(1/sqrt(1/x+1),x)

$\label{eq34}{-{\log \left({{\sqrt{{x + 1}\over x}}+ 1}\right)}+{\log \left({{\sqrt{{x + 1}\over x}}- 1}\right)}+{2 \ x \ {\sqrt{{x + 1}\over x}}}}\over 2$

(34)

Type: Union(Expression(Integer),...)

... --unknown, Wed, 23 Nov 2005 08:30:18 -0600 reply

integrate(sin(sin x), x)

... --unknown, Fri, 25 Nov 2005 16:28:37 -0600 reply

integrate(a/2(1-cos(bt)),t)

yet another test that shall work but not in maple ? --unknown, Thu, 09 Mar 2006 09:21:47 -0600 reply

integrate(tan(arctan(x)/3),x)

... --unknown, Thu, 09 Mar 2006 09:22:56 -0600 reply

integrate(tan(arctan(x)/3),x);

... --unknown, Sat, 11 Mar 2006 12:40:39 -0600 reply

integrate(x, x)

... --unknown, Sat, 11 Mar 2006 12:41:33 -0600 reply

axiom

integrate(x, x)

$\label{eq35}{1 \over 2}\ {x^2}$

(35)

Type: Polynomial(Fraction(Integer))

... --unknown, Sat, 11 Mar 2006 12:43:17 -0600 reply

axiom

integrate((1/(2*z))*z^2), z)

  Line   1: integrate((1/(2*z))*z^2), z)
           ...........................A
  Error  A: Improper syntax.
   1 error(s) parsing

... --unknown, Sat, 11 Mar 2006 12:44:05 -0600 reply

axiom

integrate((1/(2*z))*z^2, z)

$\label{eq36}{z^2}\over 4$

(36)

Type: Union(Expression(Integer),...)

... --unknown, Sat, 11 Mar 2006 12:47:35 -0600 reply

axiom

simplify((1/(2*z))*z^2)

$\label{eq37}z \over 2$

(37)

Type: Expression(Integer)

axiom

integrate((1/(2*z))*z^2, z)

$\label{eq38}{z^2}\over 4$

(38)

Type: Union(Expression(Integer),...)

... --unknown, Sat, 06 May 2006 09:17:11 -0500 reply

integrate(ln(x),x)

... --unknown, Sat, 06 May 2006 09:20:14 -0500 reply

integrate(1/x,x)

... --unknown, Sat, 06 May 2006 16:50:37 -0500 reply

axiom

integrate(0**0,x)

$\label{eq39}x$

(39)

Type: Polynomial(Fraction(Integer))

from fr.sci.maths --unknown, Tue, 09 May 2006 09:56:50 -0500 reply

axiom

integrate( ln(y)^3/(y*(y-1)),y)

   There are no library operations named ln
      Use HyperDoc Browse or issue
                                 )what op ln
      to learn if there is any operation containing " ln " in its name.

   Cannot find a definition or applicable library operation named ln
      with argument type(s)
                                 Variable(y)

      Perhaps you should use "@" to indicate the required return type,
      or "$" to specify which version of the function you need.

from fr.sci.maths --unknown, Tue, 09 May 2006 09:58:11 -0500 reply

axiom

integrate( log(y)^3/(y*(y-1)),y)

$\label{eq40}\int^{ \displaystyle y}{{{{\log \left({\%I}\right)}^3}\over{{\%I^2}- \%I}}\ {d \%I}}$

(40)

Type: Union(Expression(Integer),...)

... --unknown, Mon, 29 May 2006 14:20:28 -0500 reply

axiom

integrate(exp(-x^2),x=0..%plusInfinity)

$\label{eq41}{\sqrt{\pi}}\over 2$

(41)

Type: Union(f1: OrderedCompletion(Expression(Integer)),...)

... --unknown, Mon, 29 May 2006 14:21:39 -0500 reply

integrate(x*2exp(-x^2),x=0..%plusInfinity)

test --unknown, Wed, 19 Jul 2006 11:59:36 -0500 reply

No ; after command or else output is supressed.

axiom

integrate(exp(%i*2*%pi*f*t), t=0..T)

$\label{eq42}{-{i \ {e^{\left(2 \ i \ T \ f \ \pi \right)}}}+ i}\over{2 \ f \ \pi}$

(42)

Type: Union(f1: OrderedCompletion(Expression(Complex(Integer))),...)

Axiom and Maxima not capable of this integrand --WinnieThePooh?, Tue, 29 May 2007 17:24:44 -0500 reply

int(exp(sin(x)),x)

reduce