|
|
|
last edited 13 years ago by Bill Page |
Edit detail for SandBoxFrobeniusAlgebra revision 7 of 26
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 | ||
|
Editor: Bill Page
Time: 2011/02/12 21:48:03 GMT-8 |
||
| Note: a more convenient notation | ||
changed: -An n-dimensional algebra is represented by a tensor $Y=\{ {y_{ij}}^k \} \ i,j,k =1,2, ... n $ viewed as an operator with two inputs 'i,j' and one output 'k'. An n-dimensional algebra is represented by a (1,2)-tensor $Y=\{ {y_k}^{ji} \} \ i,j,k =1,2, ... n $ viewed as an operator with two inputs 'i,j' and one output 'k'. For example in 2 dimensions added: )library DEXPR changed: -T:=CartesianTensor(1,n,EXPR INT) -Yijk:=unravel(concat concat - [[[script(y,[[i,j],[k]]) - for k in 1..n] - for j in 1..n] - for i in 1..n] - )$T -reindex(Yijk,[3,1,2]) -Yijk[1,1,2] -Yijk[1,2,1] -Yijk[2,1,1] -\end{axiom} -Given two vectors 'U' and 'V' -\begin{axiom} -Ui:=unravel([script(u,[[],[i]]) for i in 1..n])$T -Vj:=unravel([script(v,[[],[i]]) for i in 1..n])$T -\end{axiom} -the tensor 'Y' operates on their tensor product to yield a vector 'W' -\begin{axiom} -UVij:=product(Ui,Vj) -UVij[1,2] -UVij[2,1] -YUV:=product(Yijk,UVij) -YUV[1,1,1,1,2] -YUV[1,1,1,2,1] -YUV[1,1,2,1,1] -YUV[1,2,1,1,1] -YUV[2,1,1,1,1] -contract(contract(YUV,1,4),1,3) -contract(contract(Yijk,1,UVij,1),1,3) -Wk:=(reindex(Yijk,[3,2,1])*Ui)*Vj -\end{axiom} - -Take 2 - -An n-dimensional algebra is represented by a tensor $Y=\{ {y_k}^{ji} \} \ i,j,k =1,2, ... n $ viewed as an operator with two inputs 'i,j' and one output 'k'. -\begin{axiom} -Ykji:=unravel(concat concat T:=CartesianTensor(1,n,DEXPR INT) Y:=unravel(concat concat added: Given two vectors $U=\{ u_i \}$ and $V=\{ v_j \}$ changed: -Ui:=unravel([script(u,[[i]]) for i in 1..n])$T -Vj:=unravel([script(v,[[i]]) for i in 1..n])$T -contract(contract(Ykji,3,product(Ui,Vj),1),2,3) -Wk:=(Ykji*Ui)*Vj U:=unravel([script(u,[[i]]) for i in 1..n])$T V:=unravel([script(v,[[i]]) for i in 1..n])$T added: the tensor 'Y' operates on their tensor product to yield a vector $W=\{ w_k = {y_k}^{ji} u_i v_j \}$ \begin{axiom} W:=contract(contract(Y,3,product(U,V),1),2,3) \end{axiom} or in a more convenient notation: \begin{axiom} W:=(Y*U)*V \end{axiom}
An n-dimensional algebra is represented by a (1,2)-tensor
viewed as an operator with two inputs i,j and one
output k. For example in 2 dimensions
axiom
)library DEXPR
DistributedExpression is now explicitly exposed in frame initial DistributedExpression will be automatically loaded when needed from /var/zope2/var/LatexWiki/DEXPR.NRLIB/DEXPR n:=2
 | (1) |
Type: PositiveInteger?
axiom
T:=CartesianTensor(1,n, DEXPR INT)
 | (2) |
Type: Domain
axiom
Y:=unravel(concat concat [[[script(y,[[k], [j, i]]) for i in 1..n] for j in 1..n] for k in 1..n] )$T
![\label{eq3}\begin{array}{@{}l}
\displaystyle
\left[{\left[
\begin{array}{cc}
{y_{1}^{1, \: 1}}&{y_{1}^{1, \: 2}}
\
{y_{1}^{2, \: 1}}&{y_{1}^{2, \: 2}}](images/340718363068064613-16.0px.png "\label{eq3}\begin{array}{@{}l}
\displaystyle
\left[{\left[
\begin{array}{cc}
{y_{1}^{1, \: 1}}&{y_{1}^{1, \: 2}}
\
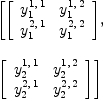{y_{1}^{2, \: 1}}&{y_{1}^{2, \: 2}}") | (3) |
Given two vectors 
and 
axiom
U:=unravel([script(u,[[i]]) for i in 1..n])$T
![\label{eq4}\left[{u_{1}}, \:{u_{2}}\right]](images/5354061332115891381-16.0px.png "\label{eq4}\left[{u_{1}}, \:{u_{2}}\right]") | (4) |
axiom
V:=unravel([script(v,[[i]]) for i in 1..n])$T
![\label{eq5}\left[{v_{1}}, \:{v_{2}}\right]](images/7175826406542591702-16.0px.png "\label{eq5}\left[{v_{1}}, \:{v_{2}}\right]") | (5) |
the tensor Y operates on their tensor product to
yield a vector 
axiom
W:=contract(contract(Y,3, product(U, V), 1), 2, 3)
![\label{eq6}\begin{array}{@{}l}
\displaystyle
\left[{{{y_{1}^{1, \: 1}}\ {u_{1}}\ {v_{1}}}+{{y_{1}^{1, \: 2}}\ {u_{2}}\ {v_{1}}}+{{y_{1}^{2, \: 1}}\ {u_{1}}\ {v_{2}}}+{{y_{1}^{2, \: 2}}\ {u_{2}}\ {v_{2}}}}, \: \right.
\
\
\displaystyle
\left.{{{y_{2}^{1, \: 1}}\ {u_{1}}\ {v_{1}}}+{{y_{2}^{1, \: 2}}\ {u_{2}}\ {v_{1}}}+{{y_{2}^{2, \: 1}}\ {u_{1}}\ {v_{2}}}+{{y_{2}^{2, \: 2}}\ {u_{2}}\ {v_{2}}}}\right]](images/5686312925399961154-16.0px.png "\label{eq6}\begin{array}{@{}l}
\displaystyle
\left[{{{y_{1}^{1, \: 1}}\ {u_{1}}\ {v_{1}}}+{{y_{1}^{1, \: 2}}\ {u_{2}}\ {v_{1}}}+{{y_{1}^{2, \: 1}}\ {u_{1}}\ {v_{2}}}+{{y_{1}^{2, \: 2}}\ {u_{2}}\ {v_{2}}}}, \: \right.
\
\
\displaystyle
\left.{{{y_{2}^{1, \: 1}}\ {u_{1}}\ {v_{1}}}+{{y_{2}^{1, \: 2}}\ {u_{2}}\ {v_{1}}}+{{y_{2}^{2, \: 1}}\ {u_{1}}\ {v_{2}}}+{{y_{2}^{2, \: 2}}\ {u_{2}}\ {v_{2}}}}\right]") | (6) |
or in a more convenient notation:
axiom
W:=(Y*U)*V
![\label{eq7}\begin{array}{@{}l}
\displaystyle
\left[{{{y_{1}^{1, \: 1}}\ {u_{1}}\ {v_{1}}}+{{y_{1}^{1, \: 2}}\ {u_{2}}\ {v_{1}}}+{{y_{1}^{2, \: 1}}\ {u_{1}}\ {v_{2}}}+{{y_{1}^{2, \: 2}}\ {u_{2}}\ {v_{2}}}}, \: \right.
\
\
\displaystyle
\left.{{{y_{2}^{1, \: 1}}\ {u_{1}}\ {v_{1}}}+{{y_{2}^{1, \: 2}}\ {u_{2}}\ {v_{1}}}+{{y_{2}^{2, \: 1}}\ {u_{1}}\ {v_{2}}}+{{y_{2}^{2, \: 2}}\ {u_{2}}\ {v_{2}}}}\right]](images/942304393785281705-16.0px.png "\label{eq7}\begin{array}{@{}l}
\displaystyle
\left[{{{y_{1}^{1, \: 1}}\ {u_{1}}\ {v_{1}}}+{{y_{1}^{1, \: 2}}\ {u_{2}}\ {v_{1}}}+{{y_{1}^{2, \: 1}}\ {u_{1}}\ {v_{2}}}+{{y_{1}^{2, \: 2}}\ {u_{2}}\ {v_{2}}}}, \: \right.
\
\
\displaystyle
\left.{{{y_{2}^{1, \: 1}}\ {u_{1}}\ {v_{1}}}+{{y_{2}^{1, \: 2}}\ {u_{2}}\ {v_{1}}}+{{y_{2}^{2, \: 1}}\ {u_{1}}\ {v_{2}}}+{{y_{2}^{2, \: 2}}\ {u_{2}}\ {v_{2}}}}\right]") | (7) |