An n-dimensional algebra is represented by a (1,2)-tensor
 viewed as an operator with two inputs
viewed as an operator with two inputs i,j and one
output k. For example in 2 dimensions
axiom
)library DEXPR
DistributedExpression is now explicitly exposed in frame initial
DistributedExpression will be automatically loaded when needed from
/var/zope2/var/LatexWiki/DEXPR.NRLIB/DEXPR
n:=2
axiom
T:=CartesianTensor(1,n,FRAC POLY INT)
Type: Domain
axiom
--T:=CartesianTensor(1,n,HDMP(concat[concat concat
-- [[[script(y,[[k],[j,i]])
-- for i in 1..n]
-- for j in 1..n]
-- for k in 1..n],
-- [script(u,[[i]]) for i in 1..n],
-- [script(v,[[i]]) for i in 1..n] ],FRAC
INT))
Y:T := unravel(concat concat
[[[script(y,[[k],[j,i]])
for i in 1..n]
for j in 1..n]
for k in 1..n]
)
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
Given two vectors  and
and 
axiom
U:T := unravel([script(u,[[i]]) for i in 1..n])
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
axiom
V:T := unravel([script(v,[[i]]) for i in 1..n])
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
the tensor Y operates on their tensor product to
yield a vector 
axiom
W:=contract(contract(Y,3,product(U,V),1),2,3)
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
Diagram:
U V
2i 3j
\ /
|
1k
W
or in a more convenient notation:
axiom
W:=(Y*U)*V
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
The algebra Y is commutative if the following tensor
(the commutator) is zero
axiom
K:=Y-reindex(Y,[1,3,2])
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
A basis for the ideal defined by the coefficients of the
commutator is given by:
axiom
C:=groebner(ravel(K))
Type: List(Polynomial(Integer))
An algebra is associative if:
Y I = I Y
Y Y
Note: right figure is mirror image of left!
2 3 6 2 5 6 2 3 4
\/ / \ \/ \ | /
\/ = \/ = \|/
\ / |
4 1 1
In other words an algebra is associative if and only
if the following (3,1)-tensor
 is zero.
is zero.
axiom
test(Y*Y = contract(product(Y,Y),3,4))
Type: Boolean
axiom
test(Y*Y = contract(Y,3,Y,1))
Type: Boolean
axiom
test(reindex(reindex(Y,[1,3,2])*reindex(Y,[1,3,2]),[1,4,3,2]) =
reindex(contract(product(Y,Y),1,5),[3,1,2,4]))
Type: Boolean
axiom
test(reindex(reindex(Y,[1,3,2])*reindex(Y,[1,3,2]),[1,4,3,2]) = reindex(contract(Y,1,Y,2),[3,1,2,4]))
Type: Boolean
axiom
AA := reindex(reindex(Y,[1,3,2])*reindex(Y,[1,3,2]),[1,4,3,2])-Y*Y;
ravel(AA)
Type: List(Fraction(Polynomial(Integer)))
axiom
AB:=groebner(ravel(AA))
Type: List(Polynomial(Integer))
axiom
#AB
The Jacobi identity requires the following tensor to be zero:
2 3 6 2 5 6 2 6 3
\ / / \ \ / \ \/
\/ / \ \/ \/\
\/ - \/ - \/
\ / \
4 1 4
axiom
BA := AA - reindex(contract(Y,1,Y,2),[3,1,4,2]); ravel(BA)
Type: List(Fraction(Polynomial(Integer)))
axiom
BB:=groebner(ravel(BA));
Type: List(Polynomial(Integer))
axiom
#BB
A scalar product is denoted by 
axiom
U:T := unravel(concat
[[script(u,[[],[j,i]])
for i in 1..n]
for j in 1..n]
)
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
Definition 1
We say that the scalar product is "associative" if the following
tensor equation holds:
Y I = I Y
U U
axiom
UA := reindex(reindex(U,[2,1])*reindex(Y,[1,3,2]),[3,2,1])-U*Y
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
Definition 2
An algebra with a non-degenerate associative scalar product is
called ''pre-Frobenius''.
We may consider the problem where multiplication Y is given,
and look for all associative scalar products U = U(Y) or we
may consider an scalar product U as given, and look for all
algebras Y=Y(U) such that the scalar product is associative.
This problem can be solved using linear algebra.
axiom
)expose MCALCFN
MultiVariableCalculusFunctions is now explicitly exposed in frame
initial
K := jacobian(ravel(UA),concat(map(variables,ravel(Y)))::List
Symbol);
Type: Matrix(Fraction(Polynomial(Integer)))
axiom
YY := transpose matrix [concat(map(variables,ravel(Y)))::List
Symbol];
Type: Matrix(Polynomial(Integer))
axiom
K::OutputForm * YY::OutputForm = 0
Type: Equation(OutputForm
?)
The matrix K transforms the coefficients of the tensor Y
into coefficients of the tensor UA. We are looking for
coefficients of the tensor U such that K transforms Y
into UA=0 for any Y.
A necessary condition for the equation to have a non-trivial
solution is that the matrix K be degenerate.
Theorem 1
The scalar product of all 2-dimensional pre-Frobenius
algebras is symmetric.
Proof: Consider the determinant of the matrix K above.
axiom
Kd:DMP(concat map(variables,ravel(U)),FRAC INT) := factor determinant(K)
Type: DistributedMultivariatePolynomial
?([*002u11,
*002u12,
*002u21,
*002u22],
Fraction(Integer))
The scalar product must also be non-degenerate
axiom
Ud:DMP(concat map(variables,ravel(U)),FRAC INT) := determinant
[[U[i,j] for j in 1..n] for i in 1..n]
Type: DistributedMultivariatePolynomial
?([*002u11,
*002u12,
*002u21,
*002u22],
Fraction(Integer))
therefore U must be symmetric.
axiom
nthFactor(Kd,1)
Type: DistributedMultivariatePolynomial
?([*002u11,
*002u12,
*002u21,
*002u22],
Fraction(Integer))
axiom
US:T := unravel(map(x+->subst(x,U[2,1]=U[1,2]),ravel U))
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
Pre-Frobenius Algebras
axiom
UAS:T := unravel(map(x+->subst(x,U[2,1]=U[1,2]),ravel UA))
Type: CartesianTensor
?(1,
2,
Fraction(Polynomial(Integer)))
axiom
--solve(ravel(UAS),removeDuplicates concat map(variables,ravel(US)))
KS := jacobian(ravel(UAS),concat(map(variables,ravel(Y)))::List
Symbol);
Type: Matrix(Fraction(Polynomial(Integer)))
axiom
NS:=nullSpace(KS)
Type: List(Vector(Fraction(Polynomial(Integer))))
axiom
--map(=,concat(map(variables,ravel(Y))),
entries reduce(+,[p[i]*NS.i for i in 1..#NS])
Type: List(Fraction(Polynomial(Integer)))
![]() viewed as an operator with two inputs
viewed as an operator with two inputs 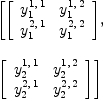
![]() and
and ![]()
![]()
![\label{eq6}\begin{array}{@{}l}
\displaystyle
\left[{{{\left({{y_{1}^{2, \: 2}}\ {u_{2}}}+{{y_{1}^{2, \: 1}}\ {u_{1}}}\right)}\ {v_{2}}}+{{\left({{y_{1}^{1, \: 2}}\ {u_{2}}}+{{y_{1}^{1, \: 1}}\ {u_{1}}}\right)}\ {v_{1}}}}, \: \right.
\
\
\displaystyle
\left.{{{\left({{y_{2}^{2, \: 2}}\ {u_{2}}}+{{y_{2}^{2, \: 1}}\ {u_{1}}}\right)}\ {v_{2}}}+{{\left({{y_{2}^{1, \: 2}}\ {u_{2}}}+{{y_{2}^{1, \: 1}}\ {u_{1}}}\right)}\ {v_{1}}}}\right]
\label{eq6}\begin{array}{@{}l}
\displaystyle
\left[{{{\left({{y_{1}^{2, \: 2}}\ {u_{2}}}+{{y_{1}^{2, \: 1}}\ {u_{1}}}\right)}\ {v_{2}}}+{{\left({{y_{1}^{1, \: 2}}\ {u_{2}}}+{{y_{1}^{1, \: 1}}\ {u_{1}}}\right)}\ {v_{1}}}}, \: \right.
\
\
\displaystyle
\left.{{{\left({{y_{2}^{2, \: 2}}\ {u_{2}}}+{{y_{2}^{2, \: 1}}\ {u_{1}}}\right)}\ {v_{2}}}+{{\left({{y_{2}^{1, \: 2}}\ {u_{2}}}+{{y_{2}^{1, \: 1}}\ {u_{1}}}\right)}\ {v_{1}}}}\right]](images/6394457768484967630-16.0px.png)
![\label{eq7}\begin{array}{@{}l}
\displaystyle
\left[{{{\left({{y_{1}^{2, \: 2}}\ {u_{2}}}+{{y_{1}^{2, \: 1}}\ {u_{1}}}\right)}\ {v_{2}}}+{{\left({{y_{1}^{1, \: 2}}\ {u_{2}}}+{{y_{1}^{1, \: 1}}\ {u_{1}}}\right)}\ {v_{1}}}}, \: \right.
\
\
\displaystyle
\left.{{{\left({{y_{2}^{2, \: 2}}\ {u_{2}}}+{{y_{2}^{2, \: 1}}\ {u_{1}}}\right)}\ {v_{2}}}+{{\left({{y_{2}^{1, \: 2}}\ {u_{2}}}+{{y_{2}^{1, \: 1}}\ {u_{1}}}\right)}\ {v_{1}}}}\right]
\label{eq7}\begin{array}{@{}l}
\displaystyle
\left[{{{\left({{y_{1}^{2, \: 2}}\ {u_{2}}}+{{y_{1}^{2, \: 1}}\ {u_{1}}}\right)}\ {v_{2}}}+{{\left({{y_{1}^{1, \: 2}}\ {u_{2}}}+{{y_{1}^{1, \: 1}}\ {u_{1}}}\right)}\ {v_{1}}}}, \: \right.
\
\
\displaystyle
\left.{{{\left({{y_{2}^{2, \: 2}}\ {u_{2}}}+{{y_{2}^{2, \: 1}}\ {u_{1}}}\right)}\ {v_{2}}}+{{\left({{y_{2}^{1, \: 2}}\ {u_{2}}}+{{y_{2}^{1, \: 1}}\ {u_{1}}}\right)}\ {v_{1}}}}\right]](images/175994118741766551-16.0px.png)

![]() is zero.
is zero.
![\label{eq14}\begin{array}{@{}l}
\displaystyle
\left[{{\left({y_{1}^{2, \: 1}}-{y_{1}^{1, \: 2}}\right)}\ {y_{2}^{1, \: 1}}}, \:{-{{y_{1}^{1, \: 2}}\ {y_{2}^{1, \: 2}}}+{{y_{1}^{2, \: 2}}\ {y_{2}^{1, \: 1}}}}, \: \right.
\
\
\displaystyle
\left.{-{{y_{1}^{1, \: 2}}\ {y_{2}^{2, \: 1}}}+{{y_{1}^{2, \: 1}}\ {y_{2}^{1, \: 2}}}-{{y_{1}^{1, \: 1}}\ {y_{1}^{2, \: 1}}}+{{y_{1}^{1, \: 1}}\ {y_{1}^{1, \: 2}}}}, \right.
\
\
\displaystyle
\left.\:{-{{y_{1}^{1, \: 2}}\ {y_{2}^{2, \: 2}}}+{{y_{1}^{2, \: 2}}\ {y_{2}^{1, \: 2}}}-{{y_{1}^{1, \: 1}}\ {y_{1}^{2, \: 2}}}+{{y_{1}^{1, \: 2}}^2}}, \: \right.
\
\
\displaystyle
\left.{{{y_{1}^{2, \: 1}}\ {y_{2}^{2, \: 1}}}-{{y_{1}^{2, \: 2}}\ {y_{2}^{1, \: 1}}}}, \:{{{y_{1}^{2, \: 2}}\ {y_{2}^{2, \: 1}}}-{{y_{1}^{2, \: 2}}\ {y_{2}^{1, \: 2}}}}, \: \right.
\
\
\displaystyle
\left.{{{y_{1}^{2, \: 1}}\ {y_{2}^{2, \: 2}}}-{{y_{1}^{2, \: 2}}\ {y_{2}^{2, \: 1}}}+{{y_{1}^{1, \: 1}}\ {y_{1}^{2, \: 2}}}-{{y_{1}^{2, \: 1}}^2}}, \: \right.
\
\
\displaystyle
\left.{{\left(-{y_{1}^{2, \: 1}}+{y_{1}^{1, \: 2}}\right)}\ {y_{1}^{2, \: 2}}}, \:{{{y_{2}^{1, \: 1}}\ {y_{2}^{2, \: 1}}}-{{y_{2}^{1, \: 1}}\ {y_{2}^{1, \: 2}}}}, \: \right.
\
\
\displaystyle
\left.{{{y_{2}^{1, \: 1}}\ {y_{2}^{2, \: 2}}}-{{y_{2}^{1, \: 2}}^2}+{{y_{1}^{1, \: 1}}\ {y_{2}^{1, \: 2}}}-{{y_{1}^{1, \: 2}}\ {y_{2}^{1, \: 1}}}}, \: \right.
\
\
\displaystyle
\left.{{\left(-{y_{1}^{2, \: 1}}+{y_{1}^{1, \: 2}}\right)}\ {y_{2}^{1, \: 1}}}, \:{{{y_{1}^{1, \: 2}}\ {y_{2}^{1, \: 2}}}-{{y_{1}^{2, \: 2}}\ {y_{2}^{1, \: 1}}}}, \: \right.
\
\
\displaystyle
\left.{-{{y_{2}^{1, \: 1}}\ {y_{2}^{2, \: 2}}}+{{y_{2}^{2, \: 1}}^2}-{{y_{1}^{1, \: 1}}\ {y_{2}^{2, \: 1}}}+{{y_{1}^{2, \: 1}}\ {y_{2}^{1, \: 1}}}}, \: \right.
\
\
\displaystyle
\left.{{{\left({y_{2}^{2, \: 1}}-{y_{2}^{1, \: 2}}\right)}\ {y_{2}^{2, \: 2}}}-{{y_{1}^{1, \: 2}}\ {y_{2}^{2, \: 1}}}+{{y_{1}^{2, \: 1}}\ {y_{2}^{1, \: 2}}}}, \: \right.
\
\
\displaystyle
\left.{-{{y_{1}^{2, \: 1}}\ {y_{2}^{2, \: 1}}}+{{y_{1}^{2, \: 2}}\ {y_{2}^{1, \: 1}}}}, \: \right.
\
\
\displaystyle
\left.{-{{y_{1}^{2, \: 2}}\ {y_{2}^{2, \: 1}}}+{{y_{1}^{2, \: 2}}\ {y_{2}^{1, \: 2}}}}\right]
\label{eq14}\begin{array}{@{}l}
\displaystyle
\left[{{\left({y_{1}^{2, \: 1}}-{y_{1}^{1, \: 2}}\right)}\ {y_{2}^{1, \: 1}}}, \:{-{{y_{1}^{1, \: 2}}\ {y_{2}^{1, \: 2}}}+{{y_{1}^{2, \: 2}}\ {y_{2}^{1, \: 1}}}}, \: \right.
\
\
\displaystyle
\left.{-{{y_{1}^{1, \: 2}}\ {y_{2}^{2, \: 1}}}+{{y_{1}^{2, \: 1}}\ {y_{2}^{1, \: 2}}}-{{y_{1}^{1, \: 1}}\ {y_{1}^{2, \: 1}}}+{{y_{1}^{1, \: 1}}\ {y_{1}^{1, \: 2}}}}, \right.
\
\
\displaystyle
\left.\:{-{{y_{1}^{1, \: 2}}\ {y_{2}^{2, \: 2}}}+{{y_{1}^{2, \: 2}}\ {y_{2}^{1, \: 2}}}-{{y_{1}^{1, \: 1}}\ {y_{1}^{2, \: 2}}}+{{y_{1}^{1, \: 2}}^2}}, \: \right.
\
\
\displaystyle
\left.{{{y_{1}^{2, \: 1}}\ {y_{2}^{2, \: 1}}}-{{y_{1}^{2, \: 2}}\ {y_{2}^{1, \: 1}}}}, \:{{{y_{1}^{2, \: 2}}\ {y_{2}^{2, \: 1}}}-{{y_{1}^{2, \: 2}}\ {y_{2}^{1, \: 2}}}}, \: \right.
\
\
\displaystyle
\left.{{{y_{1}^{2, \: 1}}\ {y_{2}^{2, \: 2}}}-{{y_{1}^{2, \: 2}}\ {y_{2}^{2, \: 1}}}+{{y_{1}^{1, \: 1}}\ {y_{1}^{2, \: 2}}}-{{y_{1}^{2, \: 1}}^2}}, \: \right.
\
\
\displaystyle
\left.{{\left(-{y_{1}^{2, \: 1}}+{y_{1}^{1, \: 2}}\right)}\ {y_{1}^{2, \: 2}}}, \:{{{y_{2}^{1, \: 1}}\ {y_{2}^{2, \: 1}}}-{{y_{2}^{1, \: 1}}\ {y_{2}^{1, \: 2}}}}, \: \right.
\
\
\displaystyle
\left.{{{y_{2}^{1, \: 1}}\ {y_{2}^{2, \: 2}}}-{{y_{2}^{1, \: 2}}^2}+{{y_{1}^{1, \: 1}}\ {y_{2}^{1, \: 2}}}-{{y_{1}^{1, \: 2}}\ {y_{2}^{1, \: 1}}}}, \: \right.
\
\
\displaystyle
\left.{{\left(-{y_{1}^{2, \: 1}}+{y_{1}^{1, \: 2}}\right)}\ {y_{2}^{1, \: 1}}}, \:{{{y_{1}^{1, \: 2}}\ {y_{2}^{1, \: 2}}}-{{y_{1}^{2, \: 2}}\ {y_{2}^{1, \: 1}}}}, \: \right.
\
\
\displaystyle
\left.{-{{y_{2}^{1, \: 1}}\ {y_{2}^{2, \: 2}}}+{{y_{2}^{2, \: 1}}^2}-{{y_{1}^{1, \: 1}}\ {y_{2}^{2, \: 1}}}+{{y_{1}^{2, \: 1}}\ {y_{2}^{1, \: 1}}}}, \: \right.
\
\
\displaystyle
\left.{{{\left({y_{2}^{2, \: 1}}-{y_{2}^{1, \: 2}}\right)}\ {y_{2}^{2, \: 2}}}-{{y_{1}^{1, \: 2}}\ {y_{2}^{2, \: 1}}}+{{y_{1}^{2, \: 1}}\ {y_{2}^{1, \: 2}}}}, \: \right.
\
\
\displaystyle
\left.{-{{y_{1}^{2, \: 1}}\ {y_{2}^{2, \: 1}}}+{{y_{1}^{2, \: 2}}\ {y_{2}^{1, \: 1}}}}, \: \right.
\
\
\displaystyle
\left.{-{{y_{1}^{2, \: 2}}\ {y_{2}^{2, \: 1}}}+{{y_{1}^{2, \: 2}}\ {y_{2}^{1, \: 2}}}}\right]](images/6386659748701516582-16.0px.png)


![]()




![\label{eq27}\begin{array}{@{}l}
\displaystyle
\left[{\left[{{{u^{1, \: 1}}^2}\over{{u^{1, \: 2}}^2}}, \:{{u^{1, \: 1}}\over{u^{1, \: 2}}}, \:{{u^{1, \: 1}}\over{u^{1, \: 2}}}, \: 1, \: 0, \: 0, \: 0, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[ -{{u^{2, \: 2}}\over{u^{1, \: 2}}}, \: 0, \: 0, \: 0, \: 1, \: 0, \: 0, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[{{-{{u^{1, \: 1}}\ {u^{2, \: 2}}}+{{u^{1, \: 2}}^2}}\over{{u^{1, \: 2}}^2}}, \: -{{u^{2, \: 2}}\over{u^{1, \: 2}}}, \: -{{u^{2, \: 2}}\over{u^{1, \: 2}}}, \: 0, \: 0, \: 1, \: 1, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[{{u^{1, \: 1}}\over{u^{1, \: 2}}}, \: 1, \: 1, \: 0, \: 0, \: 0, \: 0, \: 1 \right]}\right]
\label{eq27}\begin{array}{@{}l}
\displaystyle
\left[{\left[{{{u^{1, \: 1}}^2}\over{{u^{1, \: 2}}^2}}, \:{{u^{1, \: 1}}\over{u^{1, \: 2}}}, \:{{u^{1, \: 1}}\over{u^{1, \: 2}}}, \: 1, \: 0, \: 0, \: 0, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[ -{{u^{2, \: 2}}\over{u^{1, \: 2}}}, \: 0, \: 0, \: 0, \: 1, \: 0, \: 0, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[{{-{{u^{1, \: 1}}\ {u^{2, \: 2}}}+{{u^{1, \: 2}}^2}}\over{{u^{1, \: 2}}^2}}, \: -{{u^{2, \: 2}}\over{u^{1, \: 2}}}, \: -{{u^{2, \: 2}}\over{u^{1, \: 2}}}, \: 0, \: 0, \: 1, \: 1, \: 0 \right]}, \: \right.
\
\
\displaystyle
\left.{\left[{{u^{1, \: 1}}\over{u^{1, \: 2}}}, \: 1, \: 1, \: 0, \: 0, \: 0, \: 0, \: 1 \right]}\right]](images/2409629627165335235-16.0px.png)
