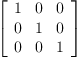FriCAS has the FriCAS interpreter for interaction with the
user and the FriCAS compiler for building library modules.
Types are one of the most important concepts in FriCAS.
Like Modula 2, PASCAL, FORTRAN, and Ada, the programming
language emphasizes strict type-checking. Unlike these
languages, types in FriCAS are dynamic objects: they are
created at run-time in response to user commands.
The FriCAS interactive language is oriented towards
ease-of-use. The FriCAS interpreter uses type-inferencing
to deduce the type of an object from user input. Type
declarations can generally be omitted for common types
in the interactive language.
The FriCAS compiler language (version 1 of the language
is called SPAD, version 2 of the language is called Aldor)
on the other hand is based on strong static types that must
be explicitly specified by the programmer.
Type Inference in the FriCAS Interpreter
Consider
fricas
(1) -> (1+2)/3
Type: Fraction(Integer)
It is sort of interesting, isn't it, that FriCAS insists on
calling "1" a fraction just because of the way it was
calculated? There is a way to say that you want the answer
as an integer. Of course this isn't always possible:
fricas
(1/3)::Integer
Cannot convert the value from type Fraction(Integer) to Integer .
But for this example it is:
fricas
((1+2)/3)::Integer
Type: Integer
FriCAS is very strict with types (meaning: that it must be
completely unambiguous where each operation takes place).
The division of 1+2 by 3 takes place in Fraction Integer
(field of rational numbers) and that is where the answer will
be, even if it is 1. Most people would automatically "retract"
this to the integer 1. But in general, there is no natural
way to do so (why not retract 1 to a natural number, for
example?). So FriCAS provides the user a way to "coerce" an
answer to another type. You can coerce 1 to any of many,
many types, for example, as a polynomial, or even as a
matrix (or the unit element of any ring).
fricas
((1+2)/3)::Polynomial Integer
Type: Polynomial(Integer)
fricas
((1+2)/3)::SquareMatrix(1,Integer)
Type: SquareMatrix
?(1,
Integer)
fricas
((1+2)/3)::SquareMatrix(3,Integer)
Type: SquareMatrix
?(3,
Integer)
fricas
((1+2)/3)::SquareMatrix(3, Polynomial Complex Integer)
Type: SquareMatrix
?(3,
Polynomial(Complex(Integer)))
Types of Objects, Domains, and Categories
In FriCAS the concept of "Type" is universally applied at
all levels.
From the FriCAS Book: Appendix B Glossary
- The type of any category is the unique symbol Category.
- The type of a domain is any category to which the domain
belongs.
- The type of any other object is either the (unique) domain
to which the object belongs or a subdomain of that domain.
- The type of objects is in general not unique.
From the FriCAS Book: Technical Introduction
Every Axiom object is an instance of some domain. That
domain is also called the type of the object. Thus the
typeOf -1 is inferred by the interpret to be Integer and
the typeOf the variable x:Integer is declared to be Integer.
Similarly the typeOf "daniel" is String. The type of an
object, however, is not unique. The type of integer 7 is
not only Integer but also NonNegativeInteger, PositiveInteger,
and possibly, in general, any other subdomain of the
domain Integer.
Domains are defined in FriCAS by programs of the form:
Name(Parameters): JoinCategorys
with Exports == Extends
add Rep := RepDomain
Implementation
The Name of each domain is used to refer to the collection
of its instances. For example, Integer denotes "the integers",
Float denotes "the floating point numbers" etc. For example:
Fraction(S: IntegralDomain): QuotientFieldCategory S with
if S has canonical and S has GcdDomain
and S has canonicalUnitNormal
then canonical
== LocalAlgebra(S, S, S) add
Rep:= Record(num:S, den:S)
coerce(d:S):% == [d,1]
zero?(x:%) == zero? x.num
Thus the type of Fraction Integer is
QuotientFieldCategory Integer with canonical.
The axiom canonical means that equal elements of the
domain are in fact identical.
We also say that the domain Fraction(S) extends the domain
LocalAlgebera(S,S,S). Domains can extend each other in a
circular mutually recursive manner so in general the extended
relationship forms a directed graph with cycles.
Fractions are represented as the domain Record(num:S, den:S).
In FriCAS domains and subdomains are themselves objects that
have types. The type of a domain or subdomain is called a
category. Categories are described by programs of the form:
Name(...): Category == JoinCategorys
with Exports
add Imports
Implementation
The type of every category is the distinguished symbol
Category. The category Name is used to denote the collection
of domains of that type. For example, category Ring denotes
the class of all rings.
For example:
QuotientFieldCategory(S: IntegralDomain): Category ==
Join(Field, Algebra S, RetractableTo S, FullyEvalableOver S,
DifferentialExtension S, FullyLinearlyExplicitRingOver S,
Patternable S, FullyPatternMatchable S) with
_/ : (S, S) -> %
++ d1 / d2 returns the fraction d1 divided by d2.
numer : % -> S
++ numer(x) returns the numerator of the fraction x.
denom : % -> S
...
if S has PolynomialFactorizationExplicit then
PolynomialFactorizationExplicit
add
import MatrixCommonDenominator(S, %)
numerator(x) == numer(x)::%
denominator(x) == denom(x) ::%
...
Categories say nothing about representation. Domains, which are
instances of category types, specify representations. See also
Rep And Per.
Categories form hierarchies (technically, directed-acyclic
graphs). A simplified hierarchical world of algebraic
categories is shown below. At the top of this world is
SetCategory, the class of algebraic sets. The notions of
parents, ancestors, and descendants is clear. Thus ordered
sets (domains of category OrderedSet) and rings are also
algebraic sets. Likewise, fields and integral domains are
rings and algebraic sets. However fields and integral
domains are not ordered sets:
SetCategory +---- Ring ---- IntegralDomain ---- Field
|
+---- Finite ---+
| \
+---- OrderedSet -----+ OrderedFinite
Figure 1. A simplified category hierarchy.
Confusion of Type and Domain
The most basic category is Type. It denotes the collection
of all domains and subdomains. Note carefully that Type does
not denote the class of all types! The type of all categories
is Category. Since Type is a category its type is Category.
fricas
typeOf(Type)
Type: Type
fricas
typeOf(typeOf(Type))
Type: Type
The second result above indicates that currently FriCAS thinks that
type of Category is again Category. However, it is safer
to treat is as undefined, because any definition leads to
paradoxes.
For example of parametric type: the domain List is able to build "lists of elements
from domain D" for arbitrary D simply by requiring that D
belong to category Type.
Another example. Enter the type Polynomial (Integer) as an
expression to FriCAS. This looks much like a function call
as well. It is! The result is stated to be of type Type.
fricas
Polynomial(Integer)
Type: Type
Ref: FriCAS Book "Chapter 2 Using Types and Modes".
Overloading and Dependent Types
Many FriCAS operations have the same name but different
types and these types can be dependent on other types.
For example
fricas
)display operation differentiate
There are 15 exposed functions called differentiate :
[1] (D,(D3 -> D3),NonNegativeInteger) -> D from D
if D has DIFEXT(D3) and D3 has RING
[2] (D,(D2 -> D2)) -> D from D if D has DIFEXT(D2) and D2 has RING
[3] (D,NonNegativeInteger) -> D from D if D has DIFRING
[4] D -> D from D if D has DIFRING
[5] (D,NonNegativeInteger) -> D from D
if D has DVARCAT(D2) and D2 has ORDSET
[6] D -> D from D if D has DVARCAT(D1) and D1 has ORDSET
[7] (D,(D3 -> D3)) -> D from D
if D has FFCAT(D2,D3,D4) and D2 has UFD and D3 has UPOLYC(
D2) and D4 has UPOLYC(FRAC(D3))
[8] (FullPartialFractionExpansion(D2,D3),NonNegativeInteger) ->
FullPartialFractionExpansion(D2,D3)
from FullPartialFractionExpansion(D2,D3)
if D2 has Join(FIELD,CHARZ) and D3 has UPOLYC(D2)
[9] FullPartialFractionExpansion(D1,D2) ->
FullPartialFractionExpansion(D1,D2)
from FullPartialFractionExpansion(D1,D2)
if D1 has Join(FIELD,CHARZ) and D2 has UPOLYC(D1)
[10] (GeneralUnivariatePowerSeries(D2,D3,D4),Variable(D3)) ->
GeneralUnivariatePowerSeries(D2,D3,D4)
from GeneralUnivariatePowerSeries(D2,D3,D4)
if D3: SYMBOL and D2 has RING and D4: D2
[11] (D,List(D3),List(NonNegativeInteger)) -> D from D
if D has PDRING(D3) and D3 has SETCAT
[12] (D,D1,NonNegativeInteger) -> D from D
if D has PDRING(D1) and D1 has SETCAT
[13] (D,List(D2)) -> D from D if D has PDRING(D2) and D2 has SETCAT
[14] (D,D1) -> D from D if D has PDRING(D1) and D1 has SETCAT
[15] (D,(D2 -> D2),D) -> D from D
if D2 has RING and D has UPOLYC(D2) and D2 has Join(SRNG,
ABELMON)
There are 14 unexposed functions called differentiate :
[1] (IntegrationResult(D1),Symbol) -> D1 from IntegrationResult(D1)
if D1 has FIELD and D1 has PDRING(SYMBOL)
[2] (IntegrationResult(D1),(D1 -> D1)) -> D1 from IntegrationResult(
D1)
if D1 has FIELD
[3] (D,PositiveInteger) -> Union(D,0) from D if D has JBC
[4] (D,D1) -> D from D if D has JBFC(D1) and D1 has JBC
[5] (OutputForm,NonNegativeInteger) -> OutputForm from OutputForm
[6] (U32Vector,Integer) -> U32Vector from
U32VectorPolynomialOperations
[7] (U32Vector,NonNegativeInteger,Integer) -> U32Vector
from U32VectorPolynomialOperations
[8] (SparseUnivariateLaurentSeries(D2,D3,D4),Variable(D3)) ->
SparseUnivariateLaurentSeries(D2,D3,D4)
from SparseUnivariateLaurentSeries(D2,D3,D4)
if D3: SYMBOL and D2 has RING and D4: D2
[9] (SparseUnivariatePuiseuxSeries(D2,D3,D4),Variable(D3)) ->
SparseUnivariatePuiseuxSeries(D2,D3,D4)
from SparseUnivariatePuiseuxSeries(D2,D3,D4)
if D3: SYMBOL and D2 has RING and D4: D2
[10] (SparseUnivariateTaylorSeries(D2,D3,D4),Variable(D3)) ->
SparseUnivariateTaylorSeries(D2,D3,D4)
from SparseUnivariateTaylorSeries(D2,D3,D4)
if D3: SYMBOL and D2 has RING and D4: D2
[11] (UnivariateFormalPowerSeries(D2),Variable(x)) ->
UnivariateFormalPowerSeries(D2)
from UnivariateFormalPowerSeries(D2) if D2 has RING
[12] (UnivariateLaurentSeries(D2,D3,D4),Variable(D3)) ->
UnivariateLaurentSeries(D2,D3,D4)
from UnivariateLaurentSeries(D2,D3,D4)
if D3: SYMBOL and D2 has RING and D4: D2
[13] (UnivariatePuiseuxSeries(D2,D3,D4),Variable(D3)) ->
UnivariatePuiseuxSeries(D2,D3,D4)
from UnivariatePuiseuxSeries(D2,D3,D4)
if D3: SYMBOL and D2 has RING and D4: D2
[14] (UnivariateTaylorSeries(D2,D3,D4),Variable(D3)) ->
UnivariateTaylorSeries(D2,D3,D4)
from UnivariateTaylorSeries(D2,D3,D4)
if D3: SYMBOL and D2 has RING and D4: D2
We can see how the interpreter resolves the type:
[14] (D,D1) -> D from D if D has PDRING D1 and D1 has SETCAT
in the following example
fricas
)set message bottomup on
Your user access level is compiler and this set option is therefore
not available. See the )set userlevel command for more
information.
differentiate(sin(x),x)
Type: Expression(Integer)
Notice that
fricas
EXPR INT has PDRING SYMBOL
Type: Boolean
fricas
SYMBOL has SETCAT
Type: Boolean
Since in FriCAS Type is class of all type one can
do
fricas
(Integer,Float)
LISP output:
(UNPRINTABLE UNPRINTABLE)
Type: Tuple(Type)
and get Tuple(Type). But one can not use categories as
FriCAS data, so `(Integer,SetCategory?)' does not work.