Edit detail for FriCAS language revision 4 of 4

FriCAS has the FriCAS interpreter for interaction with the user and the FriCAS compiler for building library modules.

FriCAS Types

Types are one of the most important concepts in FriCAS.

Like Modula 2, PASCAL, FORTRAN, and Ada, the programming language emphasizes strict type-checking. Unlike these languages, types in FriCAS are dynamic objects: they are created at run-time in response to user commands.

The FriCAS interactive language is oriented towards ease-of-use. The FriCAS interpreter uses type-inferencing to deduce the type of an object from user input. Type declarations can generally be omitted for common types in the interactive language.

The FriCAS compiler language (version 1 of the language is called SPAD, version 2 of the language is called Aldor) on the other hand is based on strong static types that must be explicitly specified by the programmer.

Type Inference in the FriCAS Interpreter

Consider

(1) -> (1+2)/3

(1)

It is sort of interesting, isn't it, that FriCAS insists on calling "1" a fraction just because of the way it was calculated? There is a way to say that you want the answer as an integer. Of course this isn't always possible:

(1/3)::Integer

   Cannot convert the value from type Fraction(Integer) to Integer .

But for this example it is:

((1+2)/3)::Integer

(2)

FriCAS is very strict with types (meaning: that it must be completely unambiguous where each operation takes place). The division of 1+2 by 3 takes place in Fraction Integer (field of rational numbers) and that is where the answer will be, even if it is 1. Most people would automatically "retract" this to the integer 1. But in general, there is no natural way to do so (why not retract 1 to a natural number, for example?). So FriCAS provides the user a way to "coerce" an answer to another type. You can coerce 1 to any of many, many types, for example, as a polynomial, or even as a matrix (or the unit element of any ring).

((1+2)/3)::Polynomial Integer

(3)

((1+2)/3)::SquareMatrix(1,Integer)

(4)

((1+2)/3)::SquareMatrix(3,Integer)

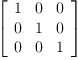(5)

((1+2)/3)::SquareMatrix(3, Polynomial Complex Integer)

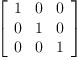(6)

Types of Objects, Domains, and Categories

In FriCAS the concept of "Type" is universally applied at all levels.

From the FriCAS Book: Appendix B Glossary

• The type of any category is the unique symbol Category.
• The type of a domain is any category to which the domain belongs.
• The type of any other object is either the (unique) domain to which the object belongs or a subdomain of that domain.
• The type of objects is in general not unique.

From the FriCAS Book: Technical Introduction

Every Axiom object is an instance of some domain. That domain is also called the type of the object. Thus the typeOf -1 is inferred by the interpret to be Integer and the typeOf the variable x:Integer is declared to be Integer. Similarly the typeOf "daniel" is String. The type of an object, however, is not unique. The type of integer 7 is not only Integer but also NonNegativeInteger, PositiveInteger, and possibly, in general, any other subdomain of the domain Integer.

Domains are defined in FriCAS by programs of the form:

  Name(Parameters): JoinCategorys
    with Exports == Extends
      add Rep := RepDomain
        Implementation 

The Name of each domain is used to refer to the collection of its instances. For example, Integer denotes "the integers", Float denotes "the floating point numbers" etc. For example:

  Fraction(S: IntegralDomain): QuotientFieldCategory S with
       if S has canonical and S has GcdDomain
         and S has canonicalUnitNormal
           then canonical
    == LocalAlgebra(S, S, S) add
      Rep:= Record(num:S, den:S)
      coerce(d:S):% == [d,1]
      zero?(x:%) == zero? x.num

Thus the type of Fraction Integer is QuotientFieldCategory Integer with canonical. The axiom canonical means that equal elements of the domain are in fact identical.

We also say that the domain Fraction(S) extends the domain LocalAlgebera(S,S,S). Domains can extend each other in a circular mutually recursive manner so in general the extended relationship forms a directed graph with cycles.

Fractions are represented as the domain Record(num:S, den:S).

In FriCAS domains and subdomains are themselves objects that have types. The type of a domain or subdomain is called a category. Categories are described by programs of the form:

   Name(...): Category == JoinCategorys
     with Exports
      add Imports
        Implementation 

The type of every category is the distinguished symbol Category. The category Name is used to denote the collection of domains of that type. For example, category Ring denotes the class of all rings.

For example:

  QuotientFieldCategory(S: IntegralDomain): Category ==
    Join(Field, Algebra S, RetractableTo S, FullyEvalableOver S,
         DifferentialExtension S, FullyLinearlyExplicitRingOver S,
           Patternable S, FullyPatternMatchable S) with
      _/     : (S, S) -> %
         ++ d1 / d2 returns the fraction d1 divided by d2.
      numer  : % -> S
         ++ numer(x) returns the numerator of the fraction x.
      denom  : % -> S
      ...
      if S has PolynomialFactorizationExplicit then
        PolynomialFactorizationExplicit
   add
      import MatrixCommonDenominator(S, %)
      numerator(x) == numer(x)::%
      denominator(x) == denom(x) ::%
      ...

Categories say nothing about representation. Domains, which are instances of category types, specify representations. See also Rep And Per.

Categories form hierarchies (technically, directed-acyclic graphs). A simplified hierarchical world of algebraic categories is shown below. At the top of this world is SetCategory, the class of algebraic sets. The notions of parents, ancestors, and descendants is clear. Thus ordered sets (domains of category OrderedSet) and rings are also algebraic sets. Likewise, fields and integral domains are rings and algebraic sets. However fields and integral domains are not ordered sets:

  SetCategory +---- Ring ---- IntegralDomain ---- Field
              |
              +----  Finite    ---+
              |                    \
              +---- OrderedSet -----+ OrderedFinite

  Figure 1. A simplified category hierarchy.

Confusion of Type and Domain

The most basic category is Type. It denotes the collection of all domains and subdomains. Note carefully that Type does not denote the class of all types! The type of all categories is Category. Since Type is a category its type is Category.

typeOf(Type)

(7)

typeOf(typeOf(Type))

(8)

The second result above indicates that currently FriCAS thinks that type of Category is again Category. However, it is safer to treat is as undefined, because any definition leads to paradoxes.

For example of parametric type: the domain List is able to build "lists of elements from domain D" for arbitrary D simply by requiring that D belong to category Type.

Another example. Enter the type Polynomial (Integer) as an expression to FriCAS. This looks much like a function call as well. It is! The result is stated to be of type Type.

Polynomial(Integer)

(9)

Ref: FriCAS Book "Chapter 2 Using Types and Modes".

Overloading and Dependent Types

Many FriCAS operations have the same name but different types and these types can be dependent on other types. For example

)display operation differentiate

There are 15 exposed functions called differentiate :
   [1] (D,(D3 -> D3),NonNegativeInteger) -> D from D
            if D has DIFEXT(D3) and D3 has RING
   [2] (D,(D2 -> D2)) -> D from D if D has DIFEXT(D2) and D2 has RING

   [3] (D,NonNegativeInteger) -> D from D if D has DIFRING
   [4] D -> D from D if D has DIFRING
   [5] (D,NonNegativeInteger) -> D from D
            if D has DVARCAT(D2) and D2 has ORDSET
   [6] D -> D from D if D has DVARCAT(D1) and D1 has ORDSET
   [7] (D,(D3 -> D3)) -> D from D
            if D has FFCAT(D2,D3,D4) and D2 has UFD and D3 has UPOLYC(
            D2) and D4 has UPOLYC(FRAC(D3))
   [8] (FullPartialFractionExpansion(D2,D3),NonNegativeInteger) -> 
            FullPartialFractionExpansion(D2,D3)
            from FullPartialFractionExpansion(D2,D3)
            if D2 has Join(FIELD,CHARZ) and D3 has UPOLYC(D2)
   [9] FullPartialFractionExpansion(D1,D2) -> 
            FullPartialFractionExpansion(D1,D2)
            from FullPartialFractionExpansion(D1,D2)
            if D1 has Join(FIELD,CHARZ) and D2 has UPOLYC(D1)
   [10] (GeneralUnivariatePowerSeries(D2,D3,D4),Variable(D3)) -> 
            GeneralUnivariatePowerSeries(D2,D3,D4)
            from GeneralUnivariatePowerSeries(D2,D3,D4)
            if D3: SYMBOL and D2 has RING and D4: D2
   [11] (D,List(D3),List(NonNegativeInteger)) -> D from D
            if D has PDRING(D3) and D3 has SETCAT
   [12] (D,D1,NonNegativeInteger) -> D from D
            if D has PDRING(D1) and D1 has SETCAT
   [13] (D,List(D2)) -> D from D if D has PDRING(D2) and D2 has SETCAT

   [14] (D,D1) -> D from D if D has PDRING(D1) and D1 has SETCAT
   [15] (D,(D2 -> D2),D) -> D from D
            if D2 has RING and D has UPOLYC(D2) and D2 has Join(SRNG,
            ABELMON)

There are 14 unexposed functions called differentiate :
   [1] (IntegrationResult(D1),Symbol) -> D1 from IntegrationResult(D1)
            if D1 has FIELD and D1 has PDRING(SYMBOL)
   [2] (IntegrationResult(D1),(D1 -> D1)) -> D1 from IntegrationResult(
            D1)
            if D1 has FIELD
   [3] (D,PositiveInteger) -> Union(D,0) from D if D has JBC
   [4] (D,D1) -> D from D if D has JBFC(D1) and D1 has JBC
   [5] (OutputForm,NonNegativeInteger) -> OutputForm from OutputForm

   [6] (U32Vector,Integer) -> U32Vector from 
            U32VectorPolynomialOperations
   [7] (U32Vector,NonNegativeInteger,Integer) -> U32Vector
            from U32VectorPolynomialOperations
   [8] (SparseUnivariateLaurentSeries(D2,D3,D4),Variable(D3)) -> 
            SparseUnivariateLaurentSeries(D2,D3,D4)
            from SparseUnivariateLaurentSeries(D2,D3,D4)
            if D3: SYMBOL and D2 has RING and D4: D2
   [9] (SparseUnivariatePuiseuxSeries(D2,D3,D4),Variable(D3)) -> 
            SparseUnivariatePuiseuxSeries(D2,D3,D4)
            from SparseUnivariatePuiseuxSeries(D2,D3,D4)
            if D3: SYMBOL and D2 has RING and D4: D2
   [10] (SparseUnivariateTaylorSeries(D2,D3,D4),Variable(D3)) -> 
            SparseUnivariateTaylorSeries(D2,D3,D4)
            from SparseUnivariateTaylorSeries(D2,D3,D4)
            if D3: SYMBOL and D2 has RING and D4: D2
   [11] (UnivariateFormalPowerSeries(D2),Variable(x)) -> 
            UnivariateFormalPowerSeries(D2)
            from UnivariateFormalPowerSeries(D2) if D2 has RING
   [12] (UnivariateLaurentSeries(D2,D3,D4),Variable(D3)) -> 
            UnivariateLaurentSeries(D2,D3,D4)
            from UnivariateLaurentSeries(D2,D3,D4)
            if D3: SYMBOL and D2 has RING and D4: D2
   [13] (UnivariatePuiseuxSeries(D2,D3,D4),Variable(D3)) -> 
            UnivariatePuiseuxSeries(D2,D3,D4)
            from UnivariatePuiseuxSeries(D2,D3,D4)
            if D3: SYMBOL and D2 has RING and D4: D2
   [14] (UnivariateTaylorSeries(D2,D3,D4),Variable(D3)) -> 
            UnivariateTaylorSeries(D2,D3,D4)
            from UnivariateTaylorSeries(D2,D3,D4)
            if D3: SYMBOL and D2 has RING and D4: D2

We can see how the interpreter resolves the type:

  [14] (D,D1) -> D from D if D has PDRING D1 and D1 has SETCAT

in the following example

)set message bottomup on

   Your user access level is compiler and this set option is therefore 
      not available. See the )set userlevel command for more 
      information.
differentiate(sin(x),x)

(10)

Notice that

EXPR INT has PDRING SYMBOL

(11)

SYMBOL has SETCAT

(12)

Since in FriCAS Type is class of all type one can do

(Integer,Float)

 LISP output:
(UNPRINTABLE UNPRINTABLE)

and get Tuple(Type). But one can not use categories as FriCAS data, so `(Integer,SetCategory?)' does not work.