The Algebra of Complex Numbers Is Frobenius In Many Ways
Linear operators over a 2-dimensional vector space representing the algebra of complex numbers
Ref:
We need the Axiom LinearOperator? library.
fricas
(1) -> )library CARTEN ARITY CMONAL CPROP CLOP CALEY
CartesianTensor is now explicitly exposed in frame initial
CartesianTensor will be automatically loaded when needed from
/var/aw/var/LatexWiki/CARTEN.NRLIB/CARTEN
Arity is now explicitly exposed in frame initial
Arity will be automatically loaded when needed from
/var/aw/var/LatexWiki/ARITY.NRLIB/ARITY
ClosedMonoidal is now explicitly exposed in frame initial
ClosedMonoidal will be automatically loaded when needed from
/var/aw/var/LatexWiki/CMONAL.NRLIB/CMONAL
ClosedProp is now explicitly exposed in frame initial
ClosedProp will be automatically loaded when needed from
/var/aw/var/LatexWiki/CPROP.NRLIB/CPROP
ClosedLinearOperator is now explicitly exposed in frame initial
ClosedLinearOperator will be automatically loaded when needed from
/var/aw/var/LatexWiki/CLOP.NRLIB/CLOP
CaleyDickson is now explicitly exposed in frame initial
CaleyDickson will be automatically loaded when needed from
/var/aw/var/LatexWiki/CALEY.NRLIB/CALEY
Use the following macros for convenient notation
fricas
-- summation
macro Σ(x,i,n)==reduce(+,[x for i in n])
Type: Void
fricas
-- list
macro Ξ(f,i,n)==[f for i in n]
Type: Void
fricas
-- subscript and superscripts
macro sb == subscript
Type: Void
fricas
macro sp == superscript
Type: Void
𝐋 is the domain of 2-dimensional linear operators over the rational functions ℚ (Expression Integer), i.e. ratio of polynomials with integer coefficients.
fricas
dim:=2
fricas
macro ℒ == List
Type: Void
fricas
macro ℂ == CaleyDickson
Type: Void
fricas
macro ℚ == Expression Integer
Type: Void
fricas
𝐋 := ClosedLinearOperator(OVAR ['1,'i], ℚ)
Type: Type
fricas
𝐞:ℒ 𝐋 := basisOut()
Type: List(ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer)))
fricas
𝐝:ℒ 𝐋 := basisIn()
Type: List(ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer)))
fricas
I:𝐋:=[1] -- identity for composition
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
X:𝐋:=[2,1] -- twist
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
V:𝐋:=ev(1) -- evaluation
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
Λ:𝐋:=co(1) -- co-evaluation
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
equate(eq)==map((x,y)+->(x=y),ravel lhs eq, ravel rhs eq);
Type: Void
Now generate structure constants for Complex Algebra
The basis consists of the real and imaginary units. We use complex multiplication to form the "multiplication table" as a matrix. Then the structure constants can be obtained by dividing each matrix entry by the list of basis vectors.
Split-complex can be specified by Caley-Dickson parameter (i2)
fricas
--i2:=sp('i,[2])
i2:= -1 -- complex
Type: Integer
fricas
QQ := ℂ(ℚ,'i,-i2);
Type: Type
Basis: Each B.i is a complex number
fricas
B:ℒ QQ := map(x +-> hyper x,1$SQMATRIX(dim,ℚ)::ℒ ℒ ℚ)
Type: List(CaleyDickson
?(Expression(Integer),
i,
1))
fricas
-- Multiplication table:
M:Matrix QQ := matrix Ξ(Ξ(B.i*B.j, i,1..dim), j,1..dim)
Type: Matrix(CaleyDickson
?(Expression(Integer),
i,
1))
fricas
-- Function to divide the matrix entries by a basis element
S(y) == map(x +-> real(x/y),M)
Type: Void
fricas
-- The result is a nested list
ѕ :=map(S,B)::ℒ ℒ ℒ ℚ
fricas
Compiling function S with type CaleyDickson(Expression(Integer),i,1)
-> Matrix(Expression(Integer))
Type: List(List(List(Expression(Integer))))
fricas
-- structure constants form a tensor operator
Y := Σ(Σ(Σ(ѕ(i)(k)(j)*𝐞.i*𝐝.j*𝐝.k, i,1..dim), j,1..dim), k,1..dim)
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
arity Y
Type: ClosedProp
?(ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer)))
fricas
matrix Ξ(Ξ((𝐞.i*𝐞.j)/Y, i,1..dim), j,1..dim)
Type: Matrix(ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer)))
Units
fricas
e:=𝐞.1; i:=𝐞.2;
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
Multiplication of arbitrary ccomplex numbers 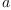 and
and 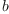
fricas
a:=Σ(sb('a,[i])*𝐞.i, i,1..dim)
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
b:=Σ(sb('b,[i])*𝐞.i, i,1..dim)
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
(a*b)/Y
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
Multiplication is Associative
fricas
test(
( I Y ) / _
( Y ) = _
( Y I ) / _
( Y ) )
Type: Boolean
A scalar product is denoted by the (2,0)-tensor
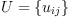
fricas
U:=Σ(Σ(script('u,[[],[i,j]])*𝐝.i*𝐝.j, i,1..dim), j,1..dim)
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
Definition 1
We say that the scalar product is associative if the tensor
equation holds:
Y = Y
U U
In other words, if the (3,0)-tensor:
(three-point function) is zero.
Using the LinearOperator? domain in Axiom and some carefully chosen symbols we can easily enter expressions that are both readable and interpreted by Axiom as "graphical calculus" diagrams describing complex products and compositions of linear operators.
fricas
ω:𝐋 :=
( Y I ) /
U -
( I Y ) /
U
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
Definition 2
An algebra with a non-degenerate associative scalar product
is called a [Frobenius Algebra]?.
The Cartan-Killing Trace
fricas
Ú:=
( Y Λ ) / _
( Y I ) / _
V
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
Ù:=
( Λ Y ) / _
( I Y ) / _
V
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
test(Ù=Ú)
Type: Boolean
forms a non-degenerate associative scalar product for Y
fricas
Ũ := Ù
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
test
( Y I ) /
Ũ =
( I Y ) /
Ũ
Type: Boolean
fricas
determinant Ξ(Ξ(retract((𝐞.i * 𝐞.j)/Ũ), j,1..dim), i,1..dim)
Type: Expression(Integer)
General Solution
We may consider the problem where multiplication Y is given,
and look for all associative scalar products 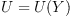
This problem can be solved using linear algebra.
fricas
)expose MCALCFN
MultiVariableCalculusFunctions is now explicitly exposed in frame
initial
J := jacobian(ravel ω,concat map(variables,ravel U)::ℒ Symbol);
Type: Matrix(Expression(Integer))
fricas
nrows(J),ncols(J)
Type: Tuple(PositiveInteger
?)
The matrix J transforms the coefficients of the tensor 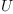 into coefficients of the tensor
into coefficients of the tensor 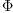 . We are looking for
the general linear family of tensors
. We are looking for
the general linear family of tensors 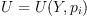 such that
such that
J transforms 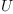 into
into 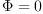 for any such
for any such 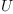 .
.
If the null space of the J matrix is not empty we can use
the basis to find all non-trivial solutions for U:
fricas
Ñ:=nullSpace(J)
Type: List(Vector(Expression(Integer)))
fricas
ℰ:=map((x,y)+->x=y, concat
map(variables,ravel U), entries Σ(sb('p,[i])*Ñ.i, i,1..#Ñ) )
Type: List(Equation(Expression(Integer)))
This defines a family of pre-Frobenius algebras:
fricas
zero? eval(ω,ℰ)
Type: Boolean
fricas
Ų:𝐋 := eval(U,ℰ)
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
Frobenius Form (co-unit)
fricas
d:=ε1*𝐝.1+εi*𝐝.2
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
𝔇:=equate(d=
( e I ) / _
Ų )
fricas
Compiling function equate with type Equation(ClosedLinearOperator(
OrderedVariableList([1,i]),Expression(Integer))) -> List(Equation
(Expression(Integer)))Type: List(Equation(Expression(Integer)))
Express scalar product in terms of Frobenius form
fricas
𝔓:=solve(𝔇,Ξ(sb('p,[i]), i,1..#Ñ)).1
Type: List(Equation(Expression(Integer)))
fricas
Ų:=eval(Ų,𝔓)
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
test
Y /
d = Ų
Type: Boolean
In general the pairing is not symmetric!
fricas
u1:=matrix Ξ(Ξ(retract((𝐞.i 𝐞.j)/Ų), i,1..dim), j,1..dim)
Type: Matrix(Expression(Integer))
The scalar product must be non-degenerate:
fricas
Ů:=determinant u1
Type: Expression(Integer)
fricas
factor(numer Ů)/factor(denom Ů)
Type: Fraction(Factored(SparseMultivariatePolynomial
?(Integer,
Kernel(Expression(Integer)))))
Cartan-Killing is a special case
fricas
ck:=solve(equate(eval(Ũ,𝔓)=Ų),[ε1,εi]).1
Type: List(Equation(Expression(Integer)))
Frobenius scalar product of complex numbers 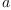 and
and 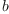
fricas
a:=sb('a,[1])*e+sb('a,[2])*i
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
b:=sb('b,[1])*e+sb('b,[2])*i
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
(a,a)/Ų
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
(b,b)/Ų
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
ab:=(a,b)/Ų
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
solve(equate(ab=0*ab),[sb('b,[1]),sb('b,[2])])
Type: List(List(Equation(Expression(Integer))))
Definition 3
Co-scalar product
Solve the [Snake Relation]? as a system of linear equations.
fricas
Ω:𝐋:=Σ(Σ(script('u,[[i,j]])*𝐞.i*𝐞.j, i,1..dim), j,1..dim)
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
ΩX:=Ω/X;
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
UXΩ:=(I*ΩX)/(Ų*I);
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
ΩXU:=(ΩX*I)/(I*Ų);
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
eq1:=equate(UXΩ=I);
Type: List(Equation(Expression(Integer)))
fricas
eq2:=equate(ΩXU=I);
Type: List(Equation(Expression(Integer)))
fricas
snake:=solve(concat(eq1,eq2),concat Ξ(Ξ(script('u,[[i,j]]), i,1..dim), j,1..dim));
Type: List(List(Equation(Expression(Integer))))
fricas
if #snake ~= 1 then error "no solution"
Type: Void
fricas
Ω:=eval(Ω,snake(1))
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
ΩX:=Ω/X;
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
The common demoninator is 
fricas
squareFreePart factor denom Ů / squareFreePart factor numer Ů
Function: squareFree : % -> Factored(%) is missing from domain: Factored(SparseMultivariatePolynomial(Integer,Kernel(Expression(Integer))))
Internal Error
The function squareFree with signature (Factored $)$ is missing from
domain Factored
(SparseMultivariatePolynomial (Integer) (Kernel (Expression (Integer))))
Check "dimension" and the snake relations.
fricas
O:𝐋:=
Ω /
Ų
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
test
( I ΩX ) /
( Ų I ) = I
Type: Boolean
fricas
test
( ΩX I ) /
( I Ų ) = I
Type: Boolean
Cartan-Killing co-scalar
fricas
eval(Ω,ck)
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
Definition 4
Co-algebra
Compute the "three-point" function and use it to define co-multiplication.
fricas
W:=
(Y I) /
Ų
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
λ:=
( ΩX I ΩX ) /
( I W I )
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
Cartan-Killing co-multiplication
fricas
eval(λ,ck)
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
test
( I ΩX ) /
( Y I ) = λ
Type: Boolean
fricas
test
( ΩX I ) /
( I Y ) = λ
Type: Boolean
Co-associativity
fricas
test(
( λ ) / _
( I λ ) = _
( λ ) / _
( λ I ) )
Type: Boolean
fricas
test
e /
λ = ΩX
Type: Boolean
Frobenius Condition (fork)
fricas
H :=
Y /
λ
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
test
( λ I ) /
( I Y ) = H
Type: Boolean
fricas
test
( I λ ) /
( Y I ) = H
Type: Boolean
The Cartan-Killing form makes H of the Frobenius condition idempotent
fricas
test( eval(H,ck)=eval(H/H,ck) )
Type: Boolean
And it is unique.
fricas
h1:=map(numer,ravel(H-H/H)::List FRAC POLY INT);
Type: List(Polynomial(Integer))
fricas
h2:=groebner h1
Type: List(Polynomial(Integer))
fricas
ck4:=solve(h2,[ε1,εi])
Type: List(List(Equation(Fraction(Polynomial(Integer)))))
fricas
test( eval(H,ck4.2)=eval(H/H,ck4.1) )
>> Error detected within library code:
catdef: division by zero
Handle
fricas
Φ :=
λ /
Y
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
The Cartan-Killing form makes Φ of the identity
fricas
test( eval(Φ,ck)=I )
Type: Boolean
and it can be the identity in only this one way.
fricas
solve(equate(Φ=I),[ε1,εi])
Type: List(List(Equation(Expression(Integer))))
If handle is identity then fork is idempotent but the converse is not true
fricas
Φ1:=map(numer,ravel(Φ-I)::List FRAC POLY INT);
Type: List(Polynomial(Integer))
fricas
Φ2:=groebner Φ1
Type: List(Polynomial(Integer))
fricas
in?(ideal h2, ideal Φ2)
Type: Boolean
fricas
in?(ideal Φ2, ideal h2)
Type: Boolean
Figure 12
fricas
φφ:= _
( Ω Ω ) / _
( X I I ) / _
( I X I ) / _
( I I X ) / _
( Y Y );
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
φφ1:=map((x:ℚ):ℚ+->numer x,φφ)
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
φφ2:=denom(ravel(φφ).1)
Type: SparseMultivariatePolynomial
?(Integer,
Kernel(Expression(Integer)))
fricas
test(φφ=(1/φφ2)*φφ1)
Type: Boolean
For Cartan-Killing this is just the co-scalar
fricas
test(eval(φφ,ck)=eval(Ω,ck))
Type: Boolean
fricas
test(eval((e,e)/H,ck)=eval(Ω,ck))
Type: Boolean
Bi-algebra conditions
fricas
ΦΦ:= _
( λ λ ) / _
( I I X ) / _
( I X I ) / _
( I I X ) / _
( Y Y ) ;
Type: ClosedLinearOperator
?(OrderedVariableList
?([1,
i]),
Expression(Integer))
fricas
test((e,e)/ΦΦ=φφ)
Type: Boolean
fricas
test(eval(ΦΦ,ck)=eval(H,ck))
Type: Boolean
fricas
test(eval(ΦΦ/(d,d),ck)=Ũ)
Type: Boolean
fricas
test(eval(H/(d,d),ck)=Ũ)
Type: Boolean
The Cartan Killing form is a bi-algebra
fricas
bi1:=map(numer,ravel(ΦΦ-H)::List FRAC POLY INT);
Type: List(Polynomial(Integer))
fricas
bi2:=groebner bi1
Type: List(Polynomial(Integer))
fricas
b:=solve( equate(ΦΦ=H), [ε1,εi] )
Type: List(List(Equation(Expression(Integer))))
fricas
test(eval(Ų, b.1)=Ũ)
Type: Boolean
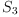 -permuted Frobenius Algebras
-permuted Frobenius Algebras![]() and
and ![]()
![]()
(2.2,0.1)(2.6,0.1)(2.6,0.9)
\psline[linewidth=0.04cm](2.4,0.3)(2.4,-0.1)
\psbezier[linewidth=0.04](2.4,-0.1)(2.4,-0.9)(3.0,-0.9)(3.0,-0.1)
\psline[linewidth=0.04cm](3.0,-0.1)(3.0,0.9)
\psbezier[linewidth=0.04](4.8,0.9)(4.8,0.1)(4.4,0.1)(4.4,0.9)
\psline[linewidth=0.04cm](4.6,0.3)(4.6,-0.1)
\psbezier[linewidth=0.04](4.6,-0.1)(4.6,-0.9)(4.0,-0.9)(4.0,-0.1)
\psline[linewidth=0.04cm](4.0,-0.1)(4.0,0.9)
\usefont{T1}{ptm}{m}{n}
\rput(3.4948437,0.205){-}
\psline[linewidth=0.04cm](0.6,-0.7)(0.6,0.9)
\psbezier[linewidth=0.04](0.0,-0.1)(0.0,-0.9)(1.2,-0.9)(1.2,-0.1)
\psline[linewidth=0.04cm](0.0,-0.1)(0.0,0.9)
\psline[linewidth=0.04cm](1.2,-0.1)(1.2,0.9)
\usefont{T1}{ptm}{m}{n}
\rput(1.6948438,0.205){=}
\end{pspicture}
}
\scalebox{1} % Change this value to rescale the drawing.
{
\begin{pspicture}(0,-0.92)(4.82,0.92)
\psbezier[linewidth=0.04](2.2,0.9)(2.2,0.1)(2.6,0.1)(2.6,0.9)
\psline[linewidth=0.04cm](2.4,0.3)(2.4,-0.1)
\psbezier[linewidth=0.04](2.4,-0.1)(2.4,-0.9)(3.0,-0.9)(3.0,-0.1)
\psline[linewidth=0.04cm](3.0,-0.1)(3.0,0.9)
\psbezier[linewidth=0.04](4.8,0.9)(4.8,0.1)(4.4,0.1)(4.4,0.9)
\psline[linewidth=0.04cm](4.6,0.3)(4.6,-0.1)
\psbezier[linewidth=0.04](4.6,-0.1)(4.6,-0.9)(4.0,-0.9)(4.0,-0.1)
\psline[linewidth=0.04cm](4.0,-0.1)(4.0,0.9)
\usefont{T1}{ptm}{m}{n}
\rput(3.4948437,0.205){-}
\psline[linewidth=0.04cm](0.6,-0.7)(0.6,0.9)
\psbezier[linewidth=0.04](0.0,-0.1)(0.0,-0.9)(1.2,-0.9)(1.2,-0.1)
\psline[linewidth=0.04cm](0.0,-0.1)(0.0,0.9)
\psline[linewidth=0.04cm](1.2,-0.1)(1.2,0.9)
\usefont{T1}{ptm}{m}{n}
\rput(1.6948438,0.205){=}
\end{pspicture}
}](images/2375189246716000159-16.0px.png)

![]()
![]() into coefficients of the tensor
into coefficients of the tensor ![]() . We are looking for
the general linear family of tensors
. We are looking for
the general linear family of tensors ![]() such that
such that
![]() into
into ![]() for any such
for any such ![]() .
.![]() and
and ![]()

![]()



