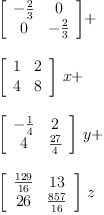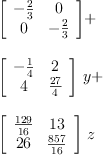help links subscribe changes refresh edit

	FrontPage
SandboxPlex ←	↑	→ SiteIndex

ScreenShots

Edit detail for ScreenShots revision 13 of 13

	1 2 3 4 5 6 7 8 9 10 11 12 13
Editor: test1 Time: 2020/11/19 17:04:52 GMT+0
Note:

changed:
-A short demonstration of Axiom
-
-  An important thing: all objects in Axiom have a <em>type</em>.  This enables us to give a simple demonstration of the Cayley-Hamilton theorem. 
-
-Let n equal 4. The semicolon at the end of the input tells Axiom not to display the result.  Thus, only its type is shown:
A short demonstration

  An important thing: all objects in FriCAS have a <em>type</em>.  This enables us to give a simple demonstration of the Cayley-Hamilton theorem. 

Let n equal 4. The semicolon at the end of the input tells FriCAS not to display the result.  Thus, only its type is shown:

changed:
-Finally we evaluate this polynomial with the original matrix as argument.  In Axiom you do not need to use parenthesis if the function takes only one argument:
Finally we evaluate this polynomial with the original matrix as argument.  In FriCAS you do not need to use parenthesis if the function takes only one argument:

changed:
-Some matrix computations under <a href="http://texmacs.org/">OldTeXmacs</a>.
Some matrix computations under <a href="http://texmacs.org/">TeXmacs</a> (this is old screenshot from Axiom era).


changed:
-Notice the hierarchical editing capabilities of OldTeXmacs.
Notice the hierarchical editing capabilities of TeXmacs (again this is old screenshot from Axiom era).

added:


changed:
-Word := OrderedFreeMonoid(Symbol)
Word := FreeMonoid(Symbol)

A short demonstration

An important thing: all objects in FriCAS have a type. This enables us to give a simple demonstration of the Cayley-Hamilton theorem.

Let n equal 4. The semicolon at the end of the input tells FriCAS not to display the result. Thus, only its type is shown:

fricas

(1) -> n := 4;

Type: PositiveInteger?

We define an abbreviation: let SM be the ring of quadratic $n\times n$ matrices with rational functions as entries:

fricas

SM ==> SquareMatrix(n, FRAC POLY INT)

Type: Void

Let M be a generic $4 \times 4$ matrix:

fricas

M: SM := matrix [[a[i,j] for j in 1..n] for i in 1..n]

$\label{eq1}\left[ \begin{array}{cccc} {a_{1, \: 1}}&{a_{1, \: 2}}&{a_{1, \: 3}}&{a_{1, \: 4}} \ {a_{2, \: 1}}&{a_{2, \: 2}}&{a_{2, \: 3}}&{a_{2, \: 4}} \ {a_{3, \: 1}}&{a_{3, \: 2}}&{a_{3, \: 3}}&{a_{3, \: 4}} \ {a_{4, \: 1}}&{a_{4, \: 2}}&{a_{4, \: 3}}&{a_{4, \: 4}}$

(1)

Type: SquareMatrix?(4,Fraction(Polynomial(Integer)))

Compute the characteristis polynomial of 'M':

fricas

P := determinant (M - x * 1);

Type: Fraction(Polynomial(Integer))

We now interpret P as univariate polynomial in x, coefficients being from the $4 \times 4$ matrices. The double colon performs this coercion:

fricas

Q := P::UP(x, SM);

Type: UnivariatePolynomial(x,SquareMatrix?(4,Fraction(Polynomial(Integer))))

Finally we evaluate this polynomial with the original matrix as argument. In FriCAS you do not need to use parenthesis if the function takes only one argument:

fricas

Q M

$\label{eq2}\left[ \begin{array}{cccc} 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0$

(2)

Type: SquareMatrix?(4,Fraction(Polynomial(Integer)))

Some matrix computations under TeXmacs (this is old screenshot from Axiom era).

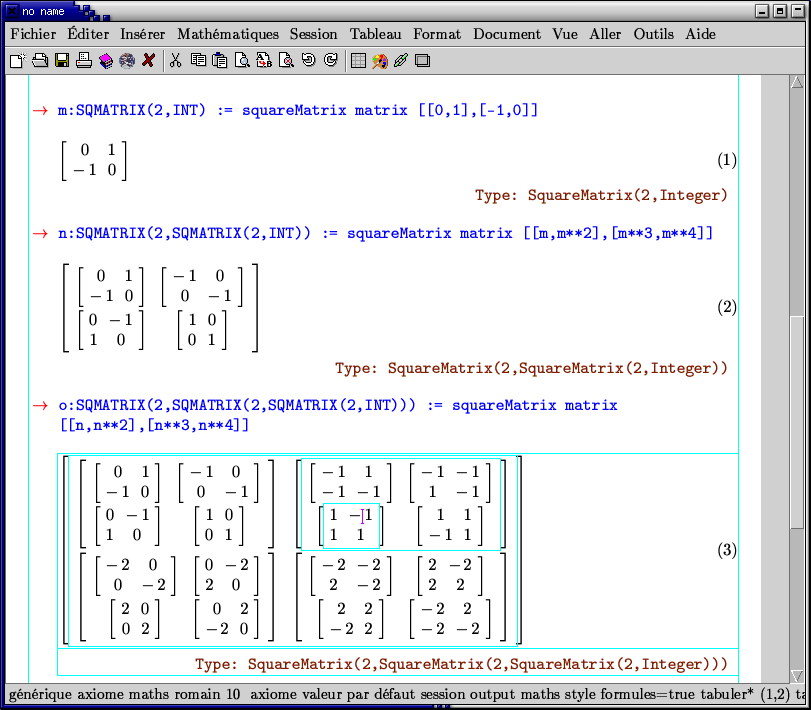
Notice the hierarchical editing capabilities of TeXmacs (again this is old screenshot from Axiom era).

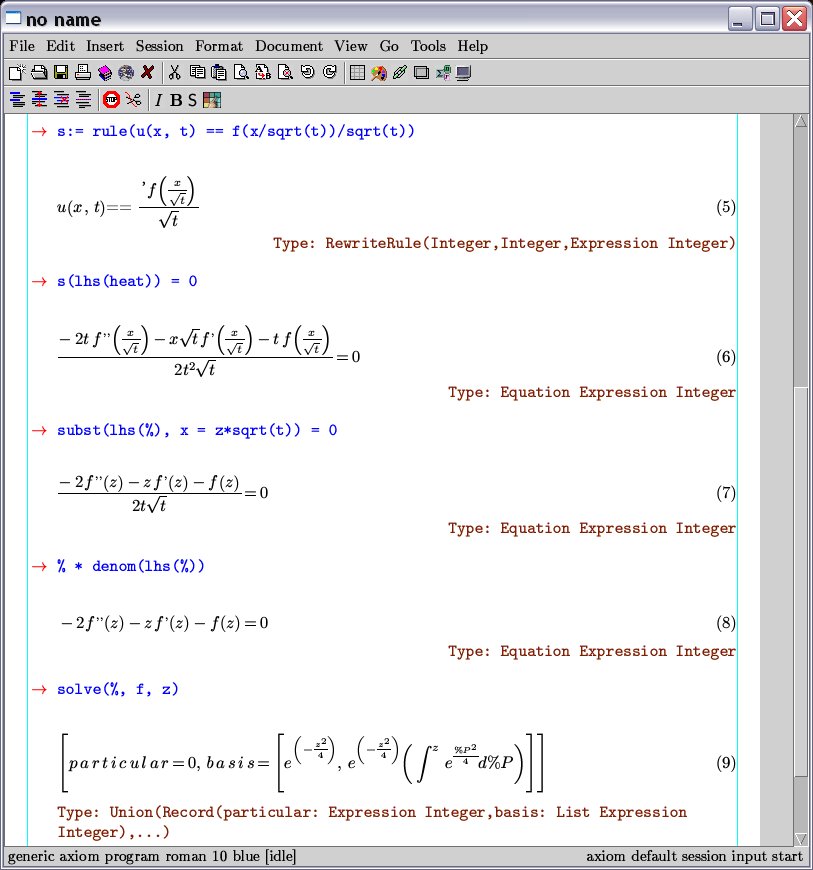
Some more complicated computations:

fricas

)cl all

   All user variables and function definitions have been cleared.
Word := FreeMonoid(Symbol)

$\label{eq3}\hbox{\axiomType{FreeMonoid}\ } \left({\hbox{\axiomType{Symbol}\ }}\right)$

(3)

Type: Type

fricas

poly:= XPR(Integer,Word)

$\label{eq4}\hbox{\axiomType{XPolynomialRing}\ } \left({\hbox{\axiomType{Integer}\ } , \:{\hbox{\axiomType{FreeMonoid}\ } \left({\hbox{\axiomType{Symbol}\ }}\right)}}\right)$

(4)

Type: Type

fricas

p:poly := 2 * x - 3 * y + 1

$\label{eq5}1 +{2 \ x}-{3 \ y}$