help links subscribe changes refresh edit

	FrontPage
SandboxPlex ←	↑	→ SiteIndex

ScreenShots

Edit detail for ScreenShots revision 8 of 13

	1 2 3 4 5 6 7 8 9 10 11 12 13
Editor: 127.0.0.1 Time: 2007/11/15 18:38:20 GMT-8
Note: re-create original screenshots page from Savannah

changed:
-  Some matrix computations under <a href="http://texmacs.org/">TeXmacs</a>.
-  <p>
-   <img src="/uploads/screenshot3.png">
-  </p>
-   Please notice the hierarchical editing capabilities of TeXmacs.
-  <p>
-   <img src="http://axiom-wiki.newsynthesis.org/uploads/screenshot3.png" />
-  </p>
Some matrix computations under <a href="http://texmacs.org/">TeXmacs</a>.
 <p>
<img src="/uploads/screenshot3.png">
 </p>
Please notice the hierarchical editing capabilities of TeXmacs.

added:

<img src="http://axiom-wiki.newsynthesis.org/uploads/screenshot2.jpg" />

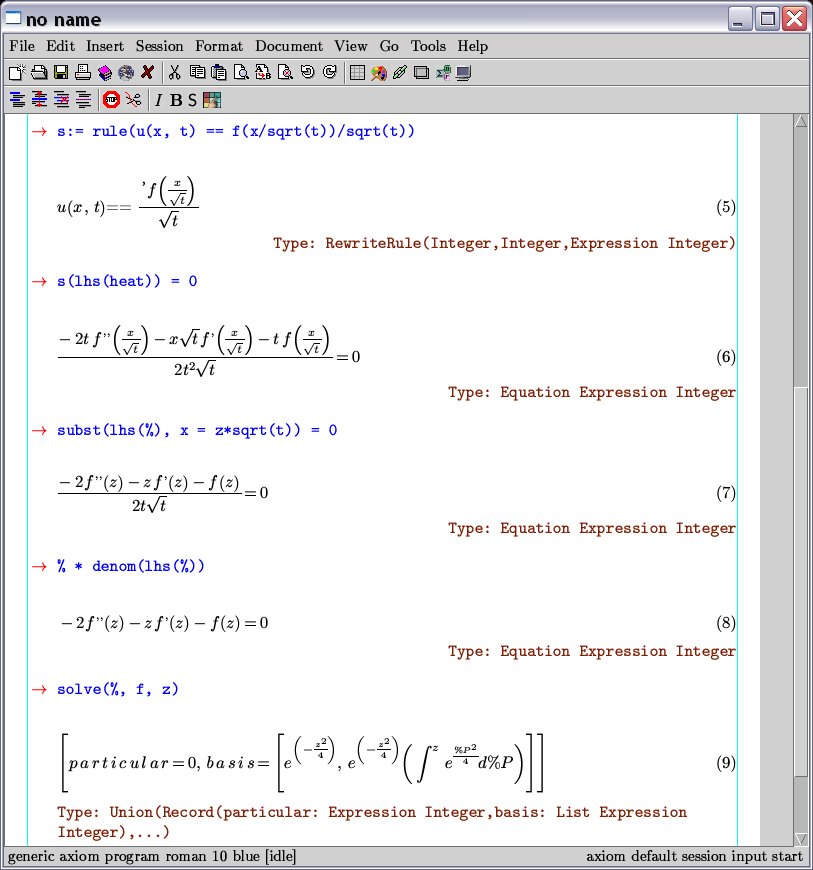
Some computations. An important thing: everything is mathematically typed in Axiom.


(1) -> 1+1

   (1)  2
                                                        Type: PositiveInteger
(2) -> integrate(1/x^(1/3),x)

         3+-+2
        3\|x
   (2)  ------
           2
                                          Type: Union(Expression Integer,...)

Axiom is running under Windows.

Some matrix computations under TeXmacs ?.

Please notice the hierarchical editing capabilities of TeXmacs?.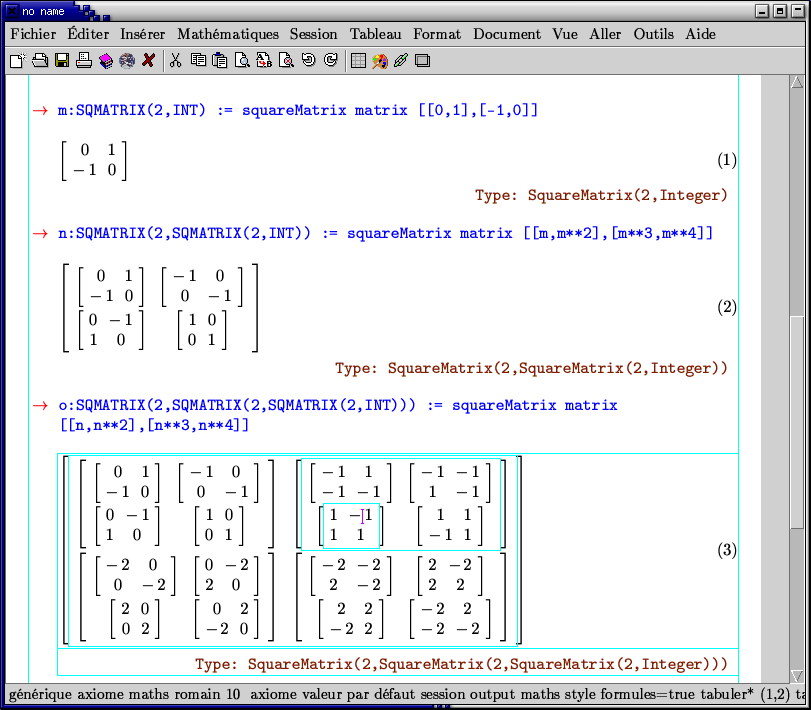

Some more complicated computations:

)cl all
 
   All user variables and function definitions have been cleared.

(1) -> Word := OrderedFreeMonoid(Symbol)
 

   (1)  OrderedFreeMonoid Symbol
                                                                 Type: Domain
(2) -> poly:= XPR(Integer,Word)
 

   (2)  XPolynomialRing(Integer,OrderedFreeMonoid Symbol)
                                                                 Type: Domain
(3) -> p:poly := 2 * x - 3 * y + 1
 

   (3)  1 + 2x - 3y
                      Type: XPolynomialRing(Integer,OrderedFreeMonoid Symbol)
(4) -> q:poly := 2 * x + 1
 

   (4)  1 + 2x
                      Type: XPolynomialRing(Integer,OrderedFreeMonoid Symbol)
(5) -> p + q
 

   (5)  2 + 4x - 3y
                      Type: XPolynomialRing(Integer,OrderedFreeMonoid Symbol)
(6) -> p * q
 

                        2
   (6)  1 + 4x - 3y + 4x  - 6y x
                      Type: XPolynomialRing(Integer,OrderedFreeMonoid Symbol)
(7) -> (p +q)^2 -p^2 -q^2 - 2*p*q
 

   (7)  - 6x y + 6y x
                      Type: XPolynomialRing(Integer,OrderedFreeMonoid Symbol)
(8) -> M := SquareMatrix(2,Fraction Integer)
 

   (8)  SquareMatrix(2,Fraction Integer)
                                                                 Type: Domain
(9) -> poly1:= XPR(M,Word)
 

   (9)
   XPolynomialRing(SquareMatrix(2,Fraction Integer),OrderedFreeMonoid Symbol)
                                                                 Type: Domain
(10) -> m1:M := matrix [[i*j**2 for i in 1..2] for j in 1..2]
 

         +1  2+
   (10)  |    |
         +4  8+
                                       Type: SquareMatrix(2,Fraction Integer)
(11) -> m2:M := m1 - 5/4
 

         +  1    +
         |- -  2 |
         |  4    |
   (11)  |       |
         |     27|
         | 4   --|
         +      4+
                                       Type: SquareMatrix(2,Fraction Integer)
(12) -> m3: M := m2**2
 

         +129     +
         |---  13 |
         | 16     |
   (12)  |        |
         |     857|
         |26   ---|
         +      16+
                                       Type: SquareMatrix(2,Fraction Integer)
(13) -> pm:poly1   := m1*x + m2*y + m3*z - 2/3
 

         +  2     +             +  1    +    +129     +
         |- -   0 |             |- -  2 |    |---  13 |
         |  3     |   +1  2+    |  4    |    | 16     |
   (13)  |        | + |    |x + |       |y + |        |z
         |       2|   +4  8+    |     27|    |     857|
         | 0   - -|             | 4   --|    |26   ---|
         +       3+             +      4+    +      16+
Type: XPolynomialRing(SquareMatrix(2,Fraction Integer),OrderedFreeMonoid Symbol)
(14) -> qm:poly1 := pm - m1*x
 

         +  2     +   +  1    +    +129     +
         |- -   0 |   |- -  2 |    |---  13 |
         |  3     |   |  4    |    | 16     |
   (14)  |        | + |       |y + |        |z
         |       2|   |     27|    |     857|
         | 0   - -|   | 4   --|    |26   ---|
         +       3+   +      4+    +      16+
Type: XPolynomialRing(SquareMatrix(2,Fraction Integer),OrderedFreeMonoid Symbol)
(15) -> qm**3
 

   (15)
     +   8      +   +  1  8+    +43   52 +    +  129       +
     |- --   0  |   |- -  -|    |--   -- |    |- ---  - 26 |
     |  27      |   |  3  3|    | 4    3 |    |   8        | 2
     |          | + |      |y + |        |z + |            |y
     |         8|   |16    |    |104  857|    |         857|
     | 0    - --|   |--   9|    |---  ---|    |- 52   - ---|
     +        27+   + 3    +    + 3    12+    +          8 +
   + 
     +  3199     831 +      +  3199     831 +      +  103169     6409 +
     |- ----   - --- |      |- ----   - --- |      |- ------   - ---- |
     |   32       4  |      |   32       4  |      |    128        4  | 2
     |               |y z + |               |z y + |                  |z
     |  831     26467|      |  831     26467|      |   6409     820977|
     |- ---   - -----|      |- ---   - -----|      | - ----   - ------|
     +   2        32 +      +   2        32 +      +     2        128 +
   + 
     +3199   831 +     +103169   6409 +      +103169   6409 +
     |----   --- |     |------   ---- |      |------   ---- |
     | 64     8  | 3   |  256      8  | 2    |  256      8  |
     |           |y  + |              |y z + |              |y z y
     |831   26467|     | 6409   820977|      | 6409   820977|
     |---   -----|     | ----   ------|      | ----   ------|
     + 4      64 +     +   4      256 +      +   4      256 +
   + 
     +3178239   795341 +       +103169   6409 +       +3178239   795341 +
     |-------   ------ |       |------   ---- |       |-------   ------ |
     |  1024      128  |   2   |  256      8  |   2   |  1024      128  |
     |                 |y z  + |              |z y  + |                 |z y z
     |795341   25447787|       | 6409   820977|       |795341   25447787|
     |------   --------|       | ----   ------|       |------   --------|
     +  64       1024  +       +   4      256 +       +  64       1024  +
   + 
     +3178239   795341 +      +98625409  12326223 +
     |-------   ------ |      |--------  -------- |
     |  1024      128  | 2    |  4096       256   | 3
     |                 |z y + |                   |z
     |795341   25447787|      |12326223  788893897|
     |------   --------|      |--------  ---------|
     +  64       1024  +      +   128       4096  +
Type: XPolynomialRing(SquareMatrix(2,Fraction Integer),OrderedFreeMonoid Symbol)

$Id: screenshots.html,v 1.8 2003/11/02 09:43:28 dmentre Exp $