login home contents what's new discussion bug reports

help links subscribe changes refresh edit

	FrontPage
SandboxPlex ←	↑	→ SiteIndex

ScreenShots

Edit detail for ScreenShots revision 11 of 13

	1 2 3 4 5 6 7 8 9 10 11 12 13
Editor: test1 Time: 2015/01/08 16:36:55 GMT+0
Note:

changed:
-Some matrix computations under <a href="http://texmacs.org/">TeXmacs</a>.
Some matrix computations under <a href="http://texmacs.org/">OldTeXmacs</a>.

changed:
-Notice the hierarchical editing capabilities of TeXmacs.
Notice the hierarchical editing capabilities of OldTeXmacs.

A short demonstration of Axiom

An important thing: all objects in Axiom have a type. This enables us to give a simple demonstration of the Cayley-Hamilton theorem.

Let n equal 4. The semicolon at the end of the input tells Axiom not to display the result. Thus, only its type is shown:

fricas

n := 4;

Type: PositiveInteger?

We define an abbreviation: let SM be the ring of quadratic $n\times n$ matrices with rational functions as entries:

fricas

SM ==> SquareMatrix(n, FRAC POLY INT)

Type: Void

Let M be a generic $4 \times 4$ matrix:

fricas

M: SM := matrix [[a[i,j] for j in 1..n] for i in 1..n]

$\label{eq1}\left[ \begin{array}{cccc} {a_{1, \: 1}}&{a_{1, \: 2}}&{a_{1, \: 3}}&{a_{1, \: 4}} \ {a_{2, \: 1}}&{a_{2, \: 2}}&{a_{2, \: 3}}&{a_{2, \: 4}} \ {a_{3, \: 1}}&{a_{3, \: 2}}&{a_{3, \: 3}}&{a_{3, \: 4}} \ {a_{4, \: 1}}&{a_{4, \: 2}}&{a_{4, \: 3}}&{a_{4, \: 4}}$

Type: SquareMatrix?(4,Fraction(Polynomial(Integer)))

Compute the characteristis polynomial of 'M':

fricas

P := determinant (M - x * 1);

Type: Fraction(Polynomial(Integer))

We now interpret P as univariate polynomial in x, coefficients being from the $4 \times 4$ matrices. The double colon performs this coercion:

fricas

Q := P::UP(x, SM);

Type: UnivariatePolynomial?(x,SquareMatrix?(4,Fraction(Polynomial(Integer))))

Finally we evaluate this polynomial with the original matrix as argument. In Axiom you do not need to use parenthesis if the function takes only one argument:

fricas

Q M

$\label{eq2}\left[ \begin{array}{cccc} 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0$

Type: SquareMatrix?(4,Fraction(Polynomial(Integer)))

Some matrix computations under OldTeXmacs ?.

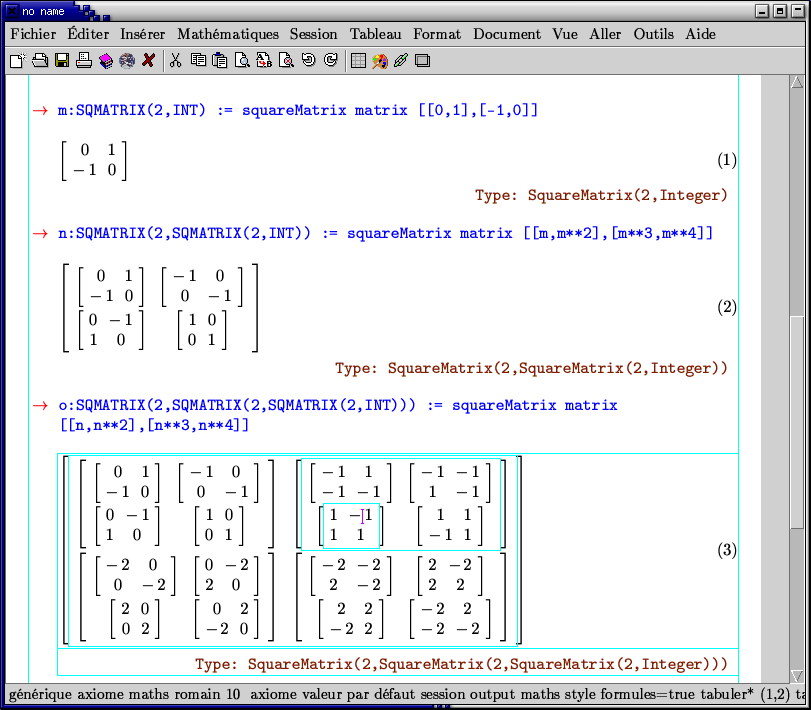
Notice the hierarchical editing capabilities of OldTeXmacs?.

Some more complicated computations:

fricas

)cl all

   All user variables and function definitions have been cleared.
Word := OrderedFreeMonoid(Symbol)

$\label{eq3}\hbox{\axiomType{OrderedFreeMonoid}\ } (\hbox{\axiomType{Symbol}\ })$

Type: Type

fricas

poly:= XPR(Integer,Word)

$\label{eq4}\hbox{\axiomType{XPolynomialRing}\ } (\hbox{\axiomType{Integer}\ } , \hbox{\axiomType{OrderedFreeMonoid}\ } (\hbox{\axiomType{Symbol}\ }))$

Type: Type

fricas

p:poly := 2 * x - 3 * y + 1

$\label{eq5}1 +{2 \ x}-{3 \ y}$

Type: XPolynomialRing?(Integer,OrderedFreeMonoid?(Symbol))

fricas

1 + 2x - 3y

   Cannot find a definition or applicable library operation named 2 
      with argument type(s) 
                                 Variable(x)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
q:poly := 2 * x + 1

$\label{eq6}1 +{2 \ x}$

Type: XPolynomialRing?(Integer,OrderedFreeMonoid?(Symbol))

fricas

p + q

$\label{eq7}2 +{4 \ x}-{3 \ y}$

Type: XPolynomialRing?(Integer,OrderedFreeMonoid?(Symbol))

fricas

p * q

$\label{eq8}1 +{4 \ x}-{3 \ y}+{4 \ {{x}^{2}}}-{6 \ y \ x}$

Type: XPolynomialRing?(Integer,OrderedFreeMonoid?(Symbol))

fricas

(p +q)^2 -p^2 -q^2 - 2*p*q

$\label{eq9}-{6 \ x \ y}+{6 \ y \ x}$

Type: XPolynomialRing?(Integer,OrderedFreeMonoid?(Symbol))

fricas

M := SquareMatrix(2,Fraction Integer)

$\label{eq10}\hbox{\axiomType{SquareMatrix}\ } (2, \hbox{\axiomType{Fraction}\ } (\hbox{\axiomType{Integer}\ }))$

Type: Type

fricas

poly1:= XPR(M,Word)

$\label{eq11}\hbox{\axiomType{XPolynomialRing}\ } (\hbox{\axiomType{SquareMatrix}\ } (2, \hbox{\axiomType{Fraction}\ } (\hbox{\axiomType{Integer}\ })) , \hbox{\axiomType{OrderedFreeMonoid}\ } (\hbox{\axiomType{Symbol}\ }))$

Type: Type

fricas

m1:M := matrix [[i*j**2 for i in 1..2] for j in 1..2]

   There are no library operations named ** 
      Use HyperDoc Browse or issue
                                 )what op **
      to learn if there is any operation containing " ** " in its name.
   Cannot find a definition or applicable library operation named ** 
      with argument type(s) 
                               PositiveInteger
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
   FriCAS will attempt to step through and interpret the code.
   There are no library operations named ** 
      Use HyperDoc Browse or issue
                                 )what op **
      to learn if there is any operation containing " ** " in its name.

   Cannot find a definition or applicable library operation named ** 
      with argument type(s) 
                               PositiveInteger
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
m2:M := m1 - 5/4

   m1 is declared as being in SquareMatrix(2,Fraction(Integer)) but has
      not been given a value.
m3: M := m2**2

   m2 is declared as being in SquareMatrix(2,Fraction(Integer)) but has
      not been given a value.
pm:poly1   := m1*x + m2*y + m3*z - 2/3

$\label{eq12}{\left[ \begin{array}{cc} -{2 \over 3}& 0 \ 0 & -{2 \over 3}$

Type: XPolynomialRing?(SquareMatrix?(2,Fraction(Integer)),OrderedFreeMonoid?(Symbol))

fricas

qm:poly1 := pm - m1*x

$\label{eq13}{\left[ \begin{array}{cc} -{2 \over 3}& 0 \ 0 & -{2 \over 3}$

Type: XPolynomialRing?(SquareMatrix?(2,Fraction(Integer)),OrderedFreeMonoid?(Symbol))

fricas

qm**3

   There are no library operations named ** 
      Use HyperDoc Browse or issue
                                 )what op **
      to learn if there is any operation containing " ** " in its name.

   Cannot find a definition or applicable library operation named ** 
      with argument type(s) 
XPolynomialRing(SquareMatrix(2,Fraction(Integer)),OrderedFreeMonoid(Symbol))
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.