help links subscribe changes refresh edit

	SandBox Categorical Relativity
SandBox Lorentz Transformations ←	↑	→ SandBoxRelativeVelocity

SandBoxLorentzTransformation

last edited 10 years ago by Bill Page

Edit detail for SandBoxLorentzTransformation revision 27 of 30

	1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Editor: page Time: 2013/10/07 06:09:41 GMT+0
Note: ω

changed:
-  An object P has a unique relative velocity w(P,Q) with respect
  An object P has a unique relative velocity ω(P,Q) with respect

changed:
-w(P,Q)==-P/dot(P,Q)-Q
-w(P,Q)
-w(S,T)
ω(P,Q)==-P/dot(P,Q)-Q
ω(P,Q)
ω(S,T)

changed:
-map(x+->Simplify x,w(U,V))
map(x+->Simplify x,ω(U,V))

changed:
-Is?(% = w(U,V))
Is?(% = ω(U,V))

changed:
-Observer P measures velocity w(Q,P). w(Q,P) is space-like
Observer P measures velocity ω(Q,P). ω(Q,P) is space-like

changed:
-dot(w(P,vect [1,0,0,0]),w(P,vect [1,0,0,0]))
dot(ω(P,vect [1,0,0,0]),ω(P,vect [1,0,0,0]))

changed:
-dot(P,w(Q,P))
-possible dot(w(Q,P),w(Q,P))::EXPR Float
-dot(Q,w(P,Q))
-possible dot(w(P,Q),w(P,Q))::EXPR Float
dot(P,ω(Q,P))
possible dot(ω(Q,P),ω(Q,P))::EXPR Float
dot(Q,ω(P,Q))
possible dot(ω(P,Q),ω(P,Q))::EXPR Float

changed:
-w(vect [u0,u1,u2,u3],vect [1,0,0,0])
-w(R,vect [1,0,0,0])
-w(S,vect [1,0,0,0])
-map(Simplify, w(U,vect [1,0,0,0]))
ω(vect [u0,u1,u2,u3],vect [1,0,0,0])
ω(R,vect [1,0,0,0])
ω(S,vect [1,0,0,0])
map(Simplify, ω(U,vect [1,0,0,0]))

changed:
-w(vect [1,0,0,0],S)
-w(vect [1,0,0,0],R)
-is?(dot(w(P,Q),w(P,Q))=dot(w(Q,P),w(Q,P)))
ω(vect [1,0,0,0],S)
ω(vect [1,0,0,0],R)
is?(dot(ω(P,Q),ω(P,Q))=dot(ω(Q,P),ω(Q,P)))

changed:
-Is?(L(P,Q)*w(P,Q) = -w(Q,P))
Is?(L(P,Q)*ω(P,Q) = -ω(Q,P))

changed:
-is?(dot(LRPQ*w(S,Q),LRPQ*w(S,Q))=dot(L(R,Q)*w(S,Q),L(R,Q)*w(S,Q)))
is?(dot(LRPQ*ω(S,Q),LRPQ*ω(S,Q))=dot(L(R,Q)*ω(S,Q),L(R,Q)*ω(S,Q)))

Lorentz transformations.

Book by T. Matolcsi

Space-time without reference frames

Mathematical Preliminaries

A vector is represented as a $n\times 1$ matrix (column vector)

fricas

Scalar := Expression Integer

$\label{eq1}\hbox{\axiomType{Expression}\ } (\hbox{\axiomType{Integer}\ })$

(1)

Type: Type

fricas

vect(x:List Scalar):Matrix Scalar == matrix map(y+->[y],x)

   Function declaration vect : List(Expression(Integer)) -> Matrix(
      Expression(Integer)) has been added to workspace.

Type: Void

fricas

vect [a0,a1,a2,a3]

fricas

Compiling function vect with type List(Expression(Integer)) -> 
      Matrix(Expression(Integer))

$\label{eq2}\left[ \begin{array}{c} a 0 \ a 1 \ a 2 \ a 3$

(2)

Type: Matrix(Expression(Integer))

Identity

fricas

ID:=diagonalMatrix([1,1,1,1])

$\label{eq3}\left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1$

(3)

Type: Matrix(Integer)

Verification

fricas

htrigs2exp == rule
  cosh(a) == (exp(a)+exp(-a))/2
  sinh(a) == (exp(a)-exp(-a))/2

Type: Void

fricas

sinhcosh == rule
  ?c*exp(a)+?c*exp(-a) == 2*c*cosh(a)
  ?c*exp(a)-?c*exp(-a) == 2*c*sinh(a)
  ?c*exp(a-b)+?c*exp(b-a) == 2*c*cosh(a-b)
  ?c*exp(a-b)-?c*exp(b-a) == 2*c*sinh(a-b)

Type: Void

fricas

expandhtrigs == rule
  cosh(:x+y) == sinh(x)*sinh(y)+cosh(x)*cosh(y)
  sinh(:x+y) == cosh(x)*sinh(y)+sinh(x)*cosh(y)
  cosh(2*x) == 2*cosh(x)^2-1
  sinh(2*x) == 2*sinh(x)*cosh(x)

Type: Void

fricas

expandhtrigs2 == rule
  cosh(2*x+2*y) == 2*cosh(x+y)^2-1
  sinh(2*x+2*y) == 2*sinh(x+y)*cosh(x+y)
  cosh(2*x-2*y) == 2*cosh(x-y)^2-1
  sinh(2*x-2*y) == 2*sinh(x-y)*cosh(x-y)

Type: Void

fricas

Simplify(x:Scalar):Scalar == htrigs sinhcosh simplify htrigs2exp x

   Function declaration Simplify : Expression(Integer) -> Expression(
      Integer) has been added to workspace.

Type: Void

fricas

possible(x)==subst(x, map(y+->(y=(random(100) - random(100))),variables x) )

Type: Void

fricas

is?(eq:Equation Scalar):Boolean == (Simplify(lhs(eq)-rhs(eq))=0)::Boolean

   Function declaration is? : Equation(Expression(Integer)) -> Boolean 
      has been added to workspace.

Type: Void

fricas

Is?(eq:Equation(Matrix(Scalar))):Boolean == _
(map(Simplify,lhs(eq)-rhs(eq)) :: Matrix Expression AlgebraicNumber = _
zero(nrows(lhs(eq)),ncols(lhs(eq)))$Matrix Expression AlgebraicNumber )::Boolean

   Function declaration Is? : Equation(Matrix(Expression(Integer))) -> 
      Boolean has been added to workspace.

Type: Void

Lorentz Form (metric)

fricas

G:=diagonalMatrix [-1,1,1,1]

$\label{eq4}\left[ \begin{array}{cccc} - 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1$

(4)

Type: Matrix(Integer)

applied to a vector produces a co-vector (represent as a $1\times n$ matrix or row vector)

fricas

g(x) == transpose(x)*G

Type: Void

fricas

g(vect [a0,a1,a2,a3])

fricas

Compiling function g with type Matrix(Expression(Integer)) -> Matrix
      (Expression(Integer))

$\label{eq5}\left[ \begin{array}{cccc} - a 0 & a 1 & a 2 & a 3$

(5)

Type: Matrix(Expression(Integer))

Scalar product

fricas

dot(x,y) == (g(x)*y)::Scalar

Type: Void

fricas

dot(vect [a0,a1,a2,a3], vect [b0,b1,b2,b3])

fricas

Compiling function dot with type (Matrix(Expression(Integer)),Matrix
      (Expression(Integer))) -> Expression(Integer)

$\label{eq6}{a 3 \ b 3}+{a 2 \ b 2}+{a 1 \ b 1}-{a 0 \ b 0}$

(6)

Type: Expression(Integer)

Tensor product

fricas

tensor(x,y) == x*g(y)

Type: Void

fricas

tensor(vect [a0,a1,a2,a3], vect [b0,b1,b2,b3])

fricas

Compiling function tensor with type (Matrix(Expression(Integer)),
      Matrix(Expression(Integer))) -> Matrix(Expression(Integer))

$\label{eq7}\left[ \begin{array}{cccc} -{a 0 \ b 0}&{a 0 \ b 1}&{a 0 \ b 2}&{a 0 \ b 3} \ -{a 1 \ b 0}&{a 1 \ b 1}&{a 1 \ b 2}&{a 1 \ b 3} \ -{a 2 \ b 0}&{a 2 \ b 1}&{a 2 \ b 2}&{a 2 \ b 3} \ -{a 3 \ b 0}&{a 3 \ b 1}&{a 3 \ b 2}&{a 3 \ b 3}$

(7)

Type: Matrix(Expression(Integer))

Massive Objects

A material object (also referred to as an observer) is represented by a time-like 4-vector

fricas

P:=vect [sqrt(p1^2+p2^2+p3^2+1),-p1,-p2,-p3];

Type: Matrix(Expression(Integer))

fricas

dot(P,P)

$\label{eq8}- 1$

(8)

Type: Expression(Integer)

fricas

Q:=vect [sqrt(q1^2+q2^2+q3^2+1),-q1,-q2,-q3];

Type: Matrix(Expression(Integer))

fricas

R:=vect [sqrt(r1^2+r2^2+r3^2+1),-r1,-r2,-r3];

Type: Matrix(Expression(Integer))

fricas

S:=1/sqrt(1-s1^2-s2^2-s3^2)*vect [1,-s1,-s2,-s3]

$\label{eq9}\left[ \begin{array}{c} {1 \over{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}} \ -{s 1 \over{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}} \ -{s 2 \over{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}} \ -{s 3 \over{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}}$

(9)

Type: Matrix(Expression(Integer))

fricas

dot(S,S)

$\label{eq10}- 1$

(10)

Type: Expression(Integer)

fricas

T:=1/sqrt(1-t1^2-t2^2-t3^2)*vect [1,-t1,-t2,-t3]

$\label{eq11}\left[ \begin{array}{c} {1 \over{\sqrt{-{{t 3}^{2}}-{{t 2}^{2}}-{{t 1}^{2}}+ 1}}} \ -{t 1 \over{\sqrt{-{{t 3}^{2}}-{{t 2}^{2}}-{{t 1}^{2}}+ 1}}} \ -{t 2 \over{\sqrt{-{{t 3}^{2}}-{{t 2}^{2}}-{{t 1}^{2}}+ 1}}} \ -{t 3 \over{\sqrt{-{{t 3}^{2}}-{{t 2}^{2}}-{{t 1}^{2}}+ 1}}}$

(11)

Type: Matrix(Expression(Integer))

fricas

U:=vect [cosh(u),sinh(u),0,0]

$\label{eq12}\left[ \begin{array}{c} {\cosh \left({u}\right)} \ {\sinh \left({u}\right)} \ 0 \ 0$

(12)

Type: Matrix(Expression(Integer))

fricas

simplify dot(U,U)

$\label{eq13}- 1$

(13)

Type: Expression(Integer)

fricas

V:=vect [cosh(v),sinh(v),0,0]

$\label{eq14}\left[ \begin{array}{c} {\cosh \left({v}\right)} \ {\sinh \left({v}\right)} \ 0 \ 0$

(14)

Type: Matrix(Expression(Integer))

fricas

Simplify dot(U,V)

fricas

Compiling body of rule htrigs2exp to compute value of type Ruleset(
      Integer,Integer,Expression(Integer))

fricas

Compiling body of rule sinhcosh to compute value of type Ruleset(
      Integer,Integer,Expression(Integer))

fricas

Compiling function Simplify with type Expression(Integer) -> 
      Expression(Integer)

$\label{eq15}-{\cosh \left({v - u}\right)}$

(15)

Type: Expression(Integer)

Observer "at rest"

fricas

vect [1,0,0,0]

$\label{eq16}\left[ \begin{array}{c} 1 \ 0 \ 0 \ 0$

(16)

Type: Matrix(Expression(Integer))

fricas

dot(%,%)

$\label{eq17}- 1$

(17)

Type: Expression(Integer)

Associated with each such vector is the orthogonal 3-d Euclidean subspace $E_P =\{x | P \cdot x = 0\}$

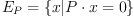
Relative Velocity

An object P has a unique relative velocity ω(P,Q) with respect to object Q given by

fricas

ω(P,Q)==-P/dot(P,Q)-Q

Type: Void

fricas

ω(P,Q)

fricas

Compiling function ω with type (Matrix(Expression(Integer)),Matrix(
      Expression(Integer))) -> Matrix(Expression(Integer))

$\label{eq18}\left[ \begin{array}{c} {{{{\left({p 3 \ q 3}+{p 2 \ q 2}+{p 1 \ q 1}\right)}\ {\sqrt{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}+ 1}}}+{{\left(-{{q 3}^{2}}-{{q 2}^{2}}-{{q 1}^{2}}\right)}\ {\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}}\over{{{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}\ {\sqrt{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}+ 1}}}-{p 3 \ q 3}-{p 2 \ q 2}-{p 1 \ q 1}}} \ {{{q 1 \ {\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}\ {\sqrt{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}+ 1}}}-{p 3 \ q 1 \ q 3}-{p 2 \ q 1 \ q 2}-{p 1 \ {{q 1}^{2}}}- p 1}\over{{{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}\ {\sqrt{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}+ 1}}}-{p 3 \ q 3}-{p 2 \ q 2}-{p 1 \ q 1}}} \ {{{q 2 \ {\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}\ {\sqrt{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}+ 1}}}-{p 3 \ q 2 \ q 3}-{p 2 \ {{q 2}^{2}}}-{p 1 \ q 1 \ q 2}- p 2}\over{{{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}\ {\sqrt{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}+ 1}}}-{p 3 \ q 3}-{p 2 \ q 2}-{p 1 \ q 1}}} \ {{{q 3 \ {\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}\ {\sqrt{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}+ 1}}}-{p 3 \ {{q 3}^{2}}}+{{\left(-{p 2 \ q 2}-{p 1 \ q 1}\right)}\ q 3}- p 3}\over{{{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}\ {\sqrt{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}+ 1}}}-{p 3 \ q 3}-{p 2 \ q 2}-{p 1 \ q 1}}}$

(18)

Type: Matrix(Expression(Integer))

fricas

ω(S,T)

$\label{eq19}\left[ \begin{array}{c} {{{{t 3}^{2}}-{s 3 \ t 3}+{{t 2}^{2}}-{s 2 \ t 2}+{{t 1}^{2}}-{s 1 \ t 1}}\over{{\left({s 3 \ t 3}+{s 2 \ t 2}+{s 1 \ t 1}- 1 \right)}\ {\sqrt{-{{t 3}^{2}}-{{t 2}^{2}}-{{t 1}^{2}}+ 1}}}} \ {{-{s 1 \ {{t 3}^{2}}}+{s 3 \ t 1 \ t 3}-{s 1 \ {{t 2}^{2}}}+{s 2 \ t 1 \ t 2}- t 1 + s 1}\over{{\left({s 3 \ t 3}+{s 2 \ t 2}+{s 1 \ t 1}- 1 \right)}\ {\sqrt{-{{t 3}^{2}}-{{t 2}^{2}}-{{t 1}^{2}}+ 1}}}} \ {{-{s 2 \ {{t 3}^{2}}}+{s 3 \ t 2 \ t 3}+{{\left({s 1 \ t 1}- 1 \right)}\ t 2}-{s 2 \ {{t 1}^{2}}}+ s 2}\over{{\left({s 3 \ t 3}+{s 2 \ t 2}+{s 1 \ t 1}- 1 \right)}\ {\sqrt{-{{t 3}^{2}}-{{t 2}^{2}}-{{t 1}^{2}}+ 1}}}} \ {{{{\left({s 2 \ t 2}+{s 1 \ t 1}- 1 \right)}\ t 3}-{s 3 \ {{t 2}^{2}}}-{s 3 \ {{t 1}^{2}}}+ s 3}\over{{\left({s 3 \ t 3}+{s 2 \ t 2}+{s 1 \ t 1}- 1 \right)}\ {\sqrt{-{{t 3}^{2}}-{{t 2}^{2}}-{{t 1}^{2}}+ 1}}}}$

(19)

Type: Matrix(Expression(Integer))

In two dimensions

fricas

map(x+->Simplify x,ω(U,V))

$\label{eq20}\left[ \begin{array}{c} {{-{\cosh \left({{2 \ v}- u}\right)}+{\cosh \left({u}\right)}}\over{2 \ {\cosh \left({v - u}\right)}}} \ {{-{\sinh \left({{2 \ v}- u}\right)}+{\sinh \left({u}\right)}}\over{2 \ {\cosh \left({v - u}\right)}}} \ 0 \ 0$

(20)

Type: Matrix(Expression(Integer))

fricas

vect [cosh(u)/cosh(u-v)-cosh(v),sinh(u)/cosh(u-v)-sinh(v),0,0]

$\label{eq21}\left[ \begin{array}{c} {{-{{\cosh \left({v - u}\right)}\ {\cosh \left({v}\right)}}+{\cosh \left({u}\right)}}\over{\cosh \left({v - u}\right)}} \ {{-{{\cosh \left({v - u}\right)}\ {\sinh \left({v}\right)}}+{\sinh \left({u}\right)}}\over{\cosh \left({v - u}\right)}} \ 0 \ 0$

(21)

Type: Matrix(Expression(Integer))

fricas

Is?(% = ω(U,V))

fricas

Compiling function Is? with type Equation(Matrix(Expression(Integer)
      )) -> Boolean

$\label{eq22} \mbox{\rm true}$

(22)

Type: Boolean

Observer P measures velocity ω(Q,P). ω(Q,P) is space-like

fricas

dot(ω(P,vect [1,0,0,0]),ω(P,vect [1,0,0,0]))

$\label{eq23}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}}\over{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}$

(23)

Type: Expression(Integer)

and in

fricas

dot(P,ω(Q,P))

$\label{eq24}0$

(24)

Type: Expression(Integer)

fricas

possible dot(ω(Q,P),ω(Q,P))::EXPR Float

fricas

Compiling function possible with type Expression(Integer) -> 
      Expression(Integer)

$\label{eq25}0.9999995659_3941083651$

(25)

Type: Expression(Float)

fricas

dot(Q,ω(P,Q))

$\label{eq26}0$

(26)

Type: Expression(Integer)

fricas

possible dot(ω(P,Q),ω(P,Q))::EXPR Float

$\label{eq27}0.9999994628_9493005142$

(27)

Type: Expression(Float)

Velocity with respect to observer "at rest"

fricas

ω(vect [u0,u1,u2,u3],vect [1,0,0,0])

$\label{eq28}\left[ \begin{array}{c} 0 \ {u 1 \over u 0} \ {u 2 \over u 0} \ {u 3 \over u 0}$

(28)

Type: Matrix(Expression(Integer))

fricas

ω(R,vect [1,0,0,0])

$\label{eq29}\left[ \begin{array}{c} 0 \ -{r 1 \over{\sqrt{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}+ 1}}} \ -{r 2 \over{\sqrt{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}+ 1}}} \ -{r 3 \over{\sqrt{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}+ 1}}}$

(29)

Type: Matrix(Expression(Integer))

fricas

ω(S,vect [1,0,0,0])

$\label{eq30}\left[ \begin{array}{c} 0 \ - s 1 \ - s 2 \ - s 3$

(30)

Type: Matrix(Expression(Integer))

fricas

map(Simplify, ω(U,vect [1,0,0,0]))

$\label{eq31}\left[ \begin{array}{c} 0 \ {{\sinh \left({u}\right)}\over{\cosh \left({u}\right)}} \ 0 \ 0$

(31)

Type: Matrix(Expression(Integer))

Non-reciprocal velocities

fricas

ω(vect [1,0,0,0],S)

$\label{eq32}\left[ \begin{array}{c} {{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}}\over{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}} \ {s 1 \over{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}} \ {s 2 \over{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}} \ {s 3 \over{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}}$

(32)

Type: Matrix(Expression(Integer))

fricas

ω(vect [1,0,0,0],R)

$\label{eq33}\left[ \begin{array}{c} {{-{{r 3}^{2}}-{{r 2}^{2}}-{{r 1}^{2}}}\over{\sqrt{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}+ 1}}} \ r 1 \ r 2 \ r 3$

(33)

Type: Matrix(Expression(Integer))

fricas

is?(dot(ω(P,Q),ω(P,Q))=dot(ω(Q,P),ω(Q,P)))

fricas

Compiling function is? with type Equation(Expression(Integer)) -> 
      Boolean

$\label{eq34} \mbox{\rm true}$

(34)

Type: Boolean

Lorentz Boost

is a linear bijection $E_Q \leftrightarrow E_P$ that preserves $E_Q \cap E_P$ and maps orthogonal compliments into each other.

fricas

L(P,Q) == ID + tensor(P+Q,P+Q)/(1-dot(P,Q)) - 2*tensor(P,Q)

Type: Void

fricas

Is?(L(P,P) = ID)

fricas

Compiling function L with type (Matrix(Expression(Integer)),Matrix(
      Expression(Integer))) -> Matrix(Expression(Integer))

$\label{eq35} \mbox{\rm true}$

(35)

Type: Boolean

fricas

Is?(L(P,Q)*L(Q,P) = ID)

$\label{eq36} \mbox{\rm true}$

(36)

Type: Boolean

fricas

Is?(L(P,Q)*Q=P)

$\label{eq37} \mbox{\rm true}$

(37)

Type: Boolean

fricas

Is?(L(P,Q)*ω(P,Q) = -ω(Q,P))

$\label{eq38} \mbox{\rm true}$

(38)

Type: Boolean

In two dimensions

fricas

map(x+->simplify expandhtrigs2 Simplify x, L(U,V))

fricas

Compiling body of rule expandhtrigs2 to compute value of type 
      Ruleset(Integer,Integer,Expression(Integer))

$\label{eq39}\left[ \begin{array}{cccc} {\cosh \left({v - u}\right)}& -{\sinh \left({v - u}\right)}& 0 & 0 \ -{\sinh \left({v - u}\right)}&{\cosh \left({v - u}\right)}& 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1$

(39)

Type: Matrix(Expression(Integer))

Composition of two Lorentz boosts is not a Lorentz boost unless all three observers are in the same plane.

fricas

Is?(L(R,P)*L(P,Q) = L(R,Q))

$\label{eq40} \mbox{\rm false}$

(40)

Type: Boolean

fricas

RQ:=a*R+b*Q;

Type: Matrix(Expression(Integer))

fricas

rq:=solve(dot(RQ,RQ)=-1,b); #rq

$\label{eq41}2$

(41)

Type: PositiveInteger?

fricas

RQ1:=eval(RQ,rq.1);

Type: Matrix(Expression(Integer))

fricas

dot(RQ1,RQ1)

$\label{eq42}- 1$

(42)

Type: Expression(Integer)

fricas

Is?(L(R,RQ1)*L(RQ1,Q) = L(R,Q))

$\label{eq43} \mbox{\rm true}$

(43)

Type: Boolean

fricas

RQ2:=eval(RQ,rq.2);

Type: Matrix(Expression(Integer))

fricas

Is?(RQ1=RQ2)

$\label{eq44} \mbox{\rm false}$

(44)

Type: Boolean

fricas

dot(RQ2,RQ2)

$\label{eq45}- 1$

(45)

Type: Expression(Integer)

fricas

Is?(L(R,RQ2)*L(RQ2,Q) = L(R,Q))

$\label{eq46} \mbox{\rm true}$

(46)

Type: Boolean

but the composition does preserve observers and magnitudes

fricas

LRPQ := L(R,P)*L(P,Q);

Type: Matrix(Expression(Integer))

fricas

Is?(LRPQ*Q = L(R,Q)*Q)

$\label{eq47} \mbox{\rm true}$

(47)

Type: Boolean

fricas

is?(dot(LRPQ*ω(S,Q),LRPQ*ω(S,Q))=dot(L(R,Q)*ω(S,Q),L(R,Q)*ω(S,Q)))

$\label{eq48} \mbox{\rm true}$

(48)

Type: Boolean

Lorentz boost with respect to observer "at rest"

fricas

LT:=L(vect [1,0,0,0],vect [u0,-u1,-u2,-u3])

$\label{eq49}\left[ \begin{array}{cccc} u 0 & u 1 & u 2 & u 3 \ u 1 &{{{{u 1}^{2}}+ u 0 + 1}\over{u 0 + 1}}&{{u 1 \ u 2}\over{u 0 + 1}}&{{u 1 \ u 3}\over{u 0 + 1}} \ u 2 &{{u 1 \ u 2}\over{u 0 + 1}}&{{{{u 2}^{2}}+ u 0 + 1}\over{u 0 + 1}}&{{u 2 \ u 3}\over{u 0 + 1}} \ u 3 &{{u 1 \ u 3}\over{u 0 + 1}}&{{u 2 \ u 3}\over{u 0 + 1}}&{{{{u 3}^{2}}+ u 0 + 1}\over{u 0 + 1}}$

(49)

Type: Matrix(Expression(Integer))

fricas

map(simplify, L(vect [1,0,0,0], map(Simplify,U)))

$\label{eq50}\left[ \begin{array}{cccc} {\cosh \left({u}\right)}& -{\sinh \left({u}\right)}& 0 & 0 \ -{\sinh \left({u}\right)}&{\cosh \left({u}\right)}& 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1$

(50)

Type: Matrix(Expression(Integer))

Two dimensional Lorentz Transformation

fricas

matrix [[1/sqrt(1-v'^2),v'/sqrt(1-v'^2),0,0],[v'/sqrt(1-v'^2),1/sqrt(1-v'^2),0,0],[0,0,1,0],[0,0,0,1]]

$\label{eq51}\left[ \begin{array}{cccc} {1 \over{\sqrt{-{{v'}^{2}}+ 1}}}&{v' \over{\sqrt{-{{v'}^{2}}+ 1}}}& 0 & 0 \ {v' \over{\sqrt{-{{v'}^{2}}+ 1}}}&{1 \over{\sqrt{-{{v'}^{2}}+ 1}}}& 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1$

(51)

Type: Matrix(Expression(Integer))

fricas

Is?(%=map(x+->eval(x,[u0=1/sqrt(1-v'^2),u1=v'/sqrt(1-v'^2),u2=0,u3=0]),LT))

$\label{eq52} \mbox{\rm true}$

(52)

Type: Boolean