help links subscribe changes refresh edit

	SandBox Categorical Relativity
SandBox Lorentz Transformations ←	↑	→ SandBoxRelativeVelocity

SandBoxLorentzTransformation

last edited 10 years ago by Bill Page

Edit detail for SandBoxLorentzTransformation revision 19 of 30

	1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30
Editor: Bill Page Time: 2013/09/25 03:25:14 GMT+0
Note: composition of boosts

changed:
-g(x)==transpose(x)*G
g(x) == transpose(x)*G

changed:
-dot(x,y)== (g(x)*y)::Expression Integer 
dot(x,y) == (g(x)*y)::Expression Integer 

added:
Non-reciprocal velocities
\begin{axiom}
v(vect [1,0,0,0],S)
v(vect [1,0,0,0],R)
is?(dot(v(P,Q),v(P,Q))=dot(v(Q,P),v(Q,P)))
\end{axiom}


added:
unless all three observers are in the same plane.

added:
RQ:=a*R+b*Q;
rq:=solve(dot(RQ,RQ)=-1,b); #rq
RQ1:=eval(RQ,rq.1);
dot(RQ1,RQ1)
Is?(L(R,RQ1)*L(RQ1,Q) = L(R,Q))
RQ2:=eval(RQ,rq.2);
Is?(RQ1=RQ2)
dot(RQ2,RQ2)
Is?(L(R,RQ2)*L(RQ2,Q) = L(R,Q))

added:

but the composition does preserve observers and magnitudes
\begin{axiom}
LRPQ := L(R,P)*L(P,Q);
Is?(LRPQ*Q = L(R,Q)*Q)
is?(dot(LRPQ*v(S,Q),LRPQ*v(S,Q))=dot(L(R,Q)*v(S,Q),L(R,Q)*v(S,Q)))
\end{axiom}

Lorentz transformations.

Book by T. Matolcsi

Space-time without reference frames

Mathematical Preliminaries

A vector is represented as a nx1 matrix (column vector)

fricas

vect(x:List Expression Integer):Matrix Expression Integer == matrix map(y+->[y],x)

   Function declaration vect : List(Expression(Integer)) -> Matrix(
      Expression(Integer)) has been added to workspace.

Type: Void

fricas

vect [a0,a1,a2,a3]

fricas

Compiling function vect with type List(Expression(Integer)) -> 
      Matrix(Expression(Integer))

$\label{eq1}\left[ \begin{array}{c} a 0 \ a 1 \ a 2 \ a 3$

(1)

Type: Matrix(Expression(Integer))

Identity

fricas

ID:=diagonalMatrix([1,1,1,1])

$\label{eq2}\left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1$

(2)

Type: Matrix(Integer)

Verification

fricas

possible(x)==subst(x, map(y+->(y=(random(100) - random(100))),variables x) )

Type: Void

fricas

is?(eq:Equation EXPR INT):Boolean == (lhs(eq)-rhs(eq)=0)::Boolean

   Function declaration is? : Equation(Expression(Integer)) -> Boolean 
      has been added to workspace.

Type: Void

fricas

Is?(eq:Equation(Matrix(EXPR(INT)))):Boolean == _
( (lhs(eq)-rhs(eq)) :: Matrix Expression AlgebraicNumber = _
zero(nrows(lhs(eq)),ncols(lhs(eq)))$Matrix Expression AlgebraicNumber )::Boolean

   Function declaration Is? : Equation(Matrix(Expression(Integer))) -> 
      Boolean has been added to workspace.

Type: Void

Lorentz Form (metric)

fricas

G:=diagonalMatrix [-1,1,1,1]

$\label{eq3}\left[ \begin{array}{cccc} - 1 & 0 & 0 & 0 \ 0 & 1 & 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1$

(3)

Type: Matrix(Integer)

applied to a vector produces a co-vector (represent as a 1xn matrix or row vector)

fricas

g(x) == transpose(x)*G

Type: Void

fricas

g(vect [a0,a1,a2,a3])

fricas

Compiling function g with type Matrix(Expression(Integer)) -> Matrix
      (Expression(Integer))

$\label{eq4}\left[ \begin{array}{cccc} - a 0 & a 1 & a 2 & a 3$

(4)

Type: Matrix(Expression(Integer))

Scalar product

fricas

dot(x,y) == (g(x)*y)::Expression Integer

Type: Void

fricas

dot(vect [a0,a1,a2,a3], vect [b0,b1,b2,b3])

fricas

Compiling function dot with type (Matrix(Expression(Integer)),Matrix
      (Expression(Integer))) -> Expression(Integer)

$\label{eq5}{a 3 \ b 3}+{a 2 \ b 2}+{a 1 \ b 1}-{a 0 \ b 0}$

(5)

Type: Expression(Integer)

Tensor product

fricas

tensor(x,y) == x*g(y)

Type: Void

fricas

tensor(vect [a0,a1,a2,a3], vect [b0,b1,b2,b3])

fricas

Compiling function tensor with type (Matrix(Expression(Integer)),
      Matrix(Expression(Integer))) -> Matrix(Expression(Integer))

$\label{eq6}\left[ \begin{array}{cccc} -{a 0 \ b 0}&{a 0 \ b 1}&{a 0 \ b 2}&{a 0 \ b 3} \ -{a 1 \ b 0}&{a 1 \ b 1}&{a 1 \ b 2}&{a 1 \ b 3} \ -{a 2 \ b 0}&{a 2 \ b 1}&{a 2 \ b 2}&{a 2 \ b 3} \ -{a 3 \ b 0}&{a 3 \ b 1}&{a 3 \ b 2}&{a 3 \ b 3}$

(6)

Type: Matrix(Expression(Integer))

Massive Objects

A material object (also referred to as an observer) is represented by a time-like 4-vector

fricas

P:=vect [sqrt(p1^2+p2^2+p3^2+1),-p1,-p2,-p3];

Type: Matrix(Expression(Integer))

fricas

dot(P,P)

$\label{eq7}- 1$

(7)

Type: Expression(Integer)

fricas

Q:=vect [sqrt(q1^2+q2^2+q3^2+1),-q1,-q2,-q3];

Type: Matrix(Expression(Integer))

fricas

R:=vect [sqrt(r1^2+r2^2+r3^2+1),-r1,-r2,-r3];

Type: Matrix(Expression(Integer))

fricas

S:=1/sqrt(1-s1^2-s2^2-s3^2)*vect [1,-s1,-s2,-s3]

$\label{eq8}\left[ \begin{array}{c} {1 \over{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}} \ -{s 1 \over{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}} \ -{s 2 \over{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}} \ -{s 3 \over{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}}$

(8)

Type: Matrix(Expression(Integer))

fricas

dot(S,S)

$\label{eq9}- 1$

(9)

Type: Expression(Integer)

fricas

T:=1/sqrt(1-t1^2-t2^2-t3^2)*vect [1,-t1,-t2,-t3]

$\label{eq10}\left[ \begin{array}{c} {1 \over{\sqrt{-{{t 3}^{2}}-{{t 2}^{2}}-{{t 1}^{2}}+ 1}}} \ -{t 1 \over{\sqrt{-{{t 3}^{2}}-{{t 2}^{2}}-{{t 1}^{2}}+ 1}}} \ -{t 2 \over{\sqrt{-{{t 3}^{2}}-{{t 2}^{2}}-{{t 1}^{2}}+ 1}}} \ -{t 3 \over{\sqrt{-{{t 3}^{2}}-{{t 2}^{2}}-{{t 1}^{2}}+ 1}}}$

(10)

Type: Matrix(Expression(Integer))

Observer "at rest"

fricas

vect [1,0,0,0]

$\label{eq11}\left[ \begin{array}{c} 1 \ 0 \ 0 \ 0$

(11)

Type: Matrix(Expression(Integer))

fricas

dot(%,%)

$\label{eq12}- 1$

(12)

Type: Expression(Integer)

Associated with each such vector is the orthogonal 3-d Euclidean subspace $E_P =\{x | P \cdot x = 0\}$

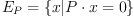
Relative Velocity

An object P has a unique relative velocity w(P,Q) with respect to object Q given by

fricas

v(P,Q)==-P/dot(P,Q)-Q

Type: Void

Observer P measures velocity v(Q,P). v(Q,P) is space-like

fricas

dot(v(P,vect [1,0,0,0]),v(P,vect [1,0,0,0]))

fricas

Compiling function v with type (Matrix(Expression(Integer)),Matrix(
      Expression(Integer))) -> Matrix(Expression(Integer))

$\label{eq13}{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}}\over{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}$

(13)

Type: Expression(Integer)

and in

fricas

dot(P,v(Q,P))

$\label{eq14}0$

(14)

Type: Expression(Integer)

fricas

possible dot(v(Q,P),v(Q,P))::EXPR Float

fricas

Compiling function possible with type Expression(Integer) -> 
      Expression(Integer)

$\label{eq15}0.9999999517_9583637853$

(15)

Type: Expression(Float)

fricas

dot(Q,v(P,Q))

$\label{eq16}0$

(16)

Type: Expression(Integer)

fricas

possible dot(v(P,Q),v(P,Q))::EXPR Float

$\label{eq17}0.9999999867_8017671721$

(17)

Type: Expression(Float)

Velocity with respect to observer "at rest"

fricas

v(vect [u0,u1,u2,u3],vect [1,0,0,0])

$\label{eq18}\left[ \begin{array}{c} 0 \ {u 1 \over u 0} \ {u 2 \over u 0} \ {u 3 \over u 0}$

(18)

Type: Matrix(Expression(Integer))

fricas

v(R,vect [1,0,0,0])

$\label{eq19}\left[ \begin{array}{c} 0 \ -{r 1 \over{\sqrt{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}+ 1}}} \ -{r 2 \over{\sqrt{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}+ 1}}} \ -{r 3 \over{\sqrt{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}+ 1}}}$

(19)

Type: Matrix(Expression(Integer))

fricas

v(S,vect [1,0,0,0])

$\label{eq20}\left[ \begin{array}{c} 0 \ - s 1 \ - s 2 \ - s 3$

(20)

Type: Matrix(Expression(Integer))

Non-reciprocal velocities

fricas

v(vect [1,0,0,0],S)

$\label{eq21}\left[ \begin{array}{c} {{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}}\over{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}} \ {s 1 \over{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}} \ {s 2 \over{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}} \ {s 3 \over{\sqrt{-{{s 3}^{2}}-{{s 2}^{2}}-{{s 1}^{2}}+ 1}}}$

(21)

Type: Matrix(Expression(Integer))

fricas

v(vect [1,0,0,0],R)

$\label{eq22}\left[ \begin{array}{c} {{-{{r 3}^{2}}-{{r 2}^{2}}-{{r 1}^{2}}}\over{\sqrt{{{r 3}^{2}}+{{r 2}^{2}}+{{r 1}^{2}}+ 1}}} \ r 1 \ r 2 \ r 3$

(22)

Type: Matrix(Expression(Integer))

fricas

is?(dot(v(P,Q),v(P,Q))=dot(v(Q,P),v(Q,P)))

fricas

Compiling function is? with type Equation(Expression(Integer)) -> 
      Boolean

$\label{eq23} \mbox{\rm true}$

(23)

Type: Boolean

Lorentz Boost

is a linear bijection $E_Q \leftrightarrow E_P$ that preserves $E_Q \cap E_P$ and maps orthogonal compliments into each other.

fricas

L(P,Q) == ID + tensor(P+Q,P+Q)/(1-dot(P,Q)) - 2*tensor(P,Q)

Type: Void

fricas

Is?(L(P,P) = ID)

fricas

Compiling function L with type (Matrix(Expression(Integer)),Matrix(
      Expression(Integer))) -> Matrix(Expression(Integer))

fricas

Compiling function Is? with type Equation(Matrix(Expression(Integer)
      )) -> Boolean

$\label{eq24} \mbox{\rm true}$

(24)

Type: Boolean

fricas

Is?(L(P,Q)*L(Q,P) = ID)

$\label{eq25} \mbox{\rm true}$

(25)

Type: Boolean

fricas

Is?(L(P,Q)*Q=P)

$\label{eq26} \mbox{\rm true}$

(26)

Type: Boolean

fricas

Is?(L(P,Q)*v(P,Q) = -v(Q,P))

$\label{eq27} \mbox{\rm true}$

(27)

Type: Boolean

Composition of two Lorentz boosts is not a Lorentz boost unless all three observers are in the same plane.

fricas

Is?(L(R,P)*L(P,Q) = L(R,Q))

$\label{eq28} \mbox{\rm false}$

(28)

Type: Boolean

fricas

RQ:=a*R+b*Q;

Type: Matrix(Expression(Integer))

fricas

rq:=solve(dot(RQ,RQ)=-1,b); #rq

$\label{eq29}2$

(29)

Type: PositiveInteger?

fricas

RQ1:=eval(RQ,rq.1);

Type: Matrix(Expression(Integer))

fricas

dot(RQ1,RQ1)

$\label{eq30}- 1$

(30)

Type: Expression(Integer)

fricas

Is?(L(R,RQ1)*L(RQ1,Q) = L(R,Q))

$\label{eq31} \mbox{\rm true}$

(31)

Type: Boolean

fricas

RQ2:=eval(RQ,rq.2);

Type: Matrix(Expression(Integer))

fricas

Is?(RQ1=RQ2)

$\label{eq32} \mbox{\rm false}$

(32)

Type: Boolean

fricas

dot(RQ2,RQ2)

$\label{eq33}- 1$

(33)

Type: Expression(Integer)

fricas

Is?(L(R,RQ2)*L(RQ2,Q) = L(R,Q))

$\label{eq34} \mbox{\rm true}$

(34)

Type: Boolean

but the composition does preserve observers and magnitudes

fricas

LRPQ := L(R,P)*L(P,Q);

Type: Matrix(Expression(Integer))

fricas

Is?(LRPQ*Q = L(R,Q)*Q)

$\label{eq35} \mbox{\rm true}$

(35)

Type: Boolean

fricas

is?(dot(LRPQ*v(S,Q),LRPQ*v(S,Q))=dot(L(R,Q)*v(S,Q),L(R,Q)*v(S,Q)))

$\label{eq36} \mbox{\rm true}$

(36)

Type: Boolean

Lorentz boost with respect to observer "at rest"

fricas

LT:=L(vect [1,0,0,0],vect [u0,-u1,-u2,-u3])

$\label{eq37}\left[ \begin{array}{cccc} u 0 & u 1 & u 2 & u 3 \ u 1 &{{{{u 1}^{2}}+ u 0 + 1}\over{u 0 + 1}}&{{u 1 \ u 2}\over{u 0 + 1}}&{{u 1 \ u 3}\over{u 0 + 1}} \ u 2 &{{u 1 \ u 2}\over{u 0 + 1}}&{{{{u 2}^{2}}+ u 0 + 1}\over{u 0 + 1}}&{{u 2 \ u 3}\over{u 0 + 1}} \ u 3 &{{u 1 \ u 3}\over{u 0 + 1}}&{{u 2 \ u 3}\over{u 0 + 1}}&{{{{u 3}^{2}}+ u 0 + 1}\over{u 0 + 1}}$

(37)

Type: Matrix(Expression(Integer))

Two dimensional Lorentz Transformation

fricas

matrix [[1/sqrt(1-v'^2),v'/sqrt(1-v'^2),0,0],[v'/sqrt(1-v'^2),1/sqrt(1-v'^2),0,0],[0,0,1,0],[0,0,0,1]]

$\label{eq38}\left[ \begin{array}{cccc} {1 \over{\sqrt{-{{v'}^{2}}+ 1}}}&{v' \over{\sqrt{-{{v'}^{2}}+ 1}}}& 0 & 0 \ {v' \over{\sqrt{-{{v'}^{2}}+ 1}}}&{1 \over{\sqrt{-{{v'}^{2}}+ 1}}}& 0 & 0 \ 0 & 0 & 1 & 0 \ 0 & 0 & 0 & 1$

(38)

Type: Matrix(Expression(Integer))

fricas

Is?(%=map(x+->eval(x,[u0=1/sqrt(1-v'^2),u1=v'/sqrt(1-v'^2),u2=0,u3=0]),LT))

$\label{eq39} \mbox{\rm true}$

(39)

Type: Boolean