Konrad Schrempf Since I never tried the ansatz (of Daniel Smertnig) and I needed something to warm up again (for programming in FriCAS) I did it now ... Factorization of non-commutative polynomialsin the free associative algebra XDPOLY using an ansatz Idea: Daniel Smertnig, January 26, 2017 Test: Konrad Schrempf, Mit 2018-07-04 10:33 Definitions fricas (1) -> --)read nc_ini03 fricas OVL ==> OrderedVariableList(ALPHABET) Type: Void
fricas OFM ==> FreeMonoid(OVL) Type: Void
fricas F ==> Integer Type: Void
fricas G ==> Fraction(Polynomial(Integer)) Type: Void
fricas XDP ==> XDPOLY(OVL, Type: Void
fricas YDP ==> XDPOLY(OVL, Type: Void
fricas --NCP ==> NCPOLY(OVL, fricas y := 'y::OFM; fricas z := 'z::OFM; fricas OF ==> OutputForm Type: Void
fricas leftSubwords(p:XDP) : List(YDP) ==
lst_wrd : List(OFM) := []
for mon in support(p) repeat
wrd := 1$OFM
for fct in factors(mon) repeat
for i in 1 .. fct.exp repeat
pos := position(wrd,
Type: Void
fricas rightSubwords(p:XDP) : List(YDP) ==
lst_wrd : List(OFM) := []
for mon in support(p) repeat
wrd := 1$OFM
for fct in reverse(factors(mon)) repeat
for i in 1 .. fct.exp repeat
pos := position(wrd,
Type: Void
fricas factorizationPolynomial(p:XDP) : YDP ==
lsw := leftSubwords(p)
rsw := rightSubwords(p)
fp := 0$YDP
for lw in lsw repeat
for rw in rsw repeat
fp := fp + lw*rw
fp
Type: Void
fricas factorizationEquations(p:XDP) : List(G) ==
lst_eqn : List(G) := []
fp := factorizationPolynomial(p)
for mon in support(fp) repeat
c_1 := coefficient(p,
Type: Void
Helper functions Lift XDP over integers to YDP over rational functions and back fricas mapPoly(p:XDP):YDP ==
if reductum p = 0 then
return leadingCoefficient(p)*leadingSupport(p)
else
return mapPoly(reductum p)+leadingCoefficient(p)*leadingSupport(p)
Type: Void
fricas mapPoly2XDP(p:YDP):XDP ==
if reductum p = 0 then
return retract(leadingCoefficient(p))*leadingSupport(p)
else
return mapPoly2XDP(reductum p)+retract(leadingCoefficient(p))*leadingSupport(p)
Type: Void
fricas vars(p)==concat map(variables, Type: Void
Example 0: fricas p0 := factorizationEquations(x::XDP) fricas Compiling function leftSubwords with type XDistributedPolynomial(
OrderedVariableList([x,fricas Compiling function rightSubwords with type XDistributedPolynomial(
OrderedVariableList([x,fricas Compiling function factorizationPolynomial with type
XDistributedPolynomial(OrderedVariableList([x,fricas Compiling function factorizationEquations with type
XDistributedPolynomial(OrderedVariableList([x,fricas Compiling function G69 with type Integer -> Boolean
Type: List(Fraction(Polynomial(Integer)))
fricas solve(p0) shows that x is irreducible ;-). Well for non-trivial polynomials solve does not work. One could try Groebner- Shirshov bases, etc. In principle it should work with general base rings, for example the integers. But I do not know the capabilities of solve. Anyway, I hope that it could be useful within XDPOLY (at least for small polynomials, because the number of non-linear equations is increasing exponentially). The file in the attachment is meant to put on github for discussions. https://github.com/billpage/ncpoly Example 1: fricas p_1 : XDP := x*(1-y*x); fricas l1 := reduce(+,
fricas r1 := reduce(+,
fricas e1 := factorizationEquations(p_1)
Type: List(Fraction(Polynomial(Integer)))
fricas concat(vars l1, fricas Compiling function vars with type XDistributedPolynomial(
OrderedVariableList([x,
Type: List(Symbol)
fricas s1:=solve(e1,
Type: List(List(Equation(Fraction(Polynomial(Integer)))))
fricas fl1:=map((x:G):G+->eval(x,
fricas fr1:=map((x:G):G+->eval(x,
fricas fl1*fr1
Example 2: fricas p_2 : XDP := x*y
fricas l2 := reduce(+,
fricas r2 := reduce(+,
fricas e2 := factorizationEquations(p_2)
Type: List(Fraction(Polynomial(Integer)))
fricas s2:=solve(e2,
Type: List(List(Equation(Fraction(Polynomial(Integer)))))
fricas fl2:=map((x:G):G+->eval(x,
fricas fr2:=map((x:G):G+->eval(x,
fricas fl2*fr2
Example 3: fricas p_3 : XDP := (x-y)*(x+y)
fricas l3 := reduce(+,
fricas r3 := reduce(+,
fricas e3 := factorizationEquations(p_3)
Type: List(Fraction(Polynomial(Integer)))
fricas s3:=solve(e3,
Type: List(List(Equation(Fraction(Polynomial(Integer)))))
fricas fl3:=map((x:G):G+->eval(x,
fricas fr3:=map((x:G):G+->eval(x,
fricas fl3*fr3
In order to obtain a solution we must choose (to omit) one variable that is necessarily not 0 since it is going to appear in the denominator of a coefficient in the result. Although this solution might be a bit "heavy" [groebnerFactorize]? expresses the solution as a union of ideals. In each ideal those variables that are necessarily zero will appear as bases containing only one variable. The remaining variables are "significant" and we can choose any of these as parameters. fricas param(e) == first variables first remove((x:G):Boolean+->#variables(x)<2, Type: Void
Example 4: fricas p_4 : XDP := (x-y^2)*(x+z^2)
fricas l4 := reduce(+,
fricas r4 := reduce(+,
fricas e4 := factorizationEquations(p_4)
Type: List(Fraction(Polynomial(Integer)))
fricas groebnerFactorize e4
Type: List(List(Polynomial(Integer)))
fricas e4a := last %
Type: List(Polynomial(Integer))
fricas param(e4a) fricas Compiling function param with type List(Polynomial(Integer)) ->
Symbol
Type: Symbol
fricas )set output tex off fricas )set output algebra on Type: List(List(Equation(Fraction(Polynomial(Integer)))))
fricas )set output tex on fricas )set output algebra off
fricas fr4:=map((x:G):G+->eval(x,
fricas fl4*fr4
fricas test(mapPoly p_4 = fl4*fr4) fricas Compiling function mapPoly with type XDistributedPolynomial(
OrderedVariableList([x,
Type: Boolean
Example 5: fricas p_5 : XDP := (x*y*z+y*x*z)*(z*x*y+z*y*x)
fricas l5 := reduce(+,
fricas r5 := reduce(+,
fricas e5 := factorizationEquations(p_5)
Type: List(Fraction(Polynomial(Integer)))
fricas )set output tex off fricas )set output algebra on Example 6: We need the solution of the factorization equations to associate a unique value with each variable. If the result includes any implicit solutions, i.e. equations whose lefthand side is not just a symbol then fricas p_6 : XDP := 2 - x^2 fricas l6 := reduce(+, fricas r6 := reduce(+, fricas e6 := factorizationEquations(p_6) Type: List(Fraction(Polynomial(Integer)))
fricas -- look for a solution for i in 1..#coefficients r6 repeat s6 := solve(e6, Type: Void
fricas s6 Type: List(List(Equation(Fraction(Polynomial(Integer)))))
Test for irreducibility. fricas map(x+->retractIfCan(lhs x)@Union(Symbol, Type: List(Boolean)
fricas if reduce(_and, Type: irreducible
|
|
|
|
last edited 7 years ago by Bill Page |
![\label{eq4}\begin{array}{@{}l}
\displaystyle
\left[{{a_{1}}\ {b_{1}}}, \:{{{a_{1}}\ {b_{2}}}+{{a_{2}}\ {b_{1}}}- 1}, \:{{a_{1}}\ {b_{3}}}, \:{{a_{3}}\ {b_{1}}}, \:{{a_{2}}\ {b_{2}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{2}}\ {b_{3}}}+{{a_{3}}\ {b_{2}}}+ 1}, \:{{a_{3}}\ {b_{3}}}\right]
\label{eq4}\begin{array}{@{}l}
\displaystyle
\left[{{a_{1}}\ {b_{1}}}, \:{{{a_{1}}\ {b_{2}}}+{{a_{2}}\ {b_{1}}}- 1}, \:{{a_{1}}\ {b_{3}}}, \:{{a_{3}}\ {b_{1}}}, \:{{a_{2}}\ {b_{2}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{2}}\ {b_{3}}}+{{a_{3}}\ {b_{2}}}+ 1}, \:{{a_{3}}\ {b_{3}}}\right]](images/5240272058223479227-16.0px.png)
![\label{eq21}\begin{array}{@{}l}
\displaystyle
\left[{{a_{1}}\ {b_{1}}}, \:{{{a_{1}}\ {b_{3}}}+{{a_{3}}\ {b_{1}}}}, \:{{{a_{1}}\ {b_{2}}}+{{a_{2}}\ {b_{1}}}}, \:{{{a_{3}}\ {b_{3}}}+ 1}, \:{{{a_{3}}\ {b_{2}}}+ 1}, \: \right.
\
\
\displaystyle
\left.{{{a_{2}}\ {b_{3}}}- 1}, \:{{{a_{2}}\ {b_{2}}}- 1}\right]
\label{eq21}\begin{array}{@{}l}
\displaystyle
\left[{{a_{1}}\ {b_{1}}}, \:{{{a_{1}}\ {b_{3}}}+{{a_{3}}\ {b_{1}}}}, \:{{{a_{1}}\ {b_{2}}}+{{a_{2}}\ {b_{1}}}}, \:{{{a_{3}}\ {b_{3}}}+ 1}, \:{{{a_{3}}\ {b_{2}}}+ 1}, \: \right.
\
\
\displaystyle
\left.{{{a_{2}}\ {b_{3}}}- 1}, \:{{{a_{2}}\ {b_{2}}}- 1}\right]](images/6091178162252775626-16.0px.png)
![\label{eq29}\begin{array}{@{}l}
\displaystyle
\left[{{a_{1}}\ {b_{1}}}, \:{{a_{1}}\ {b_{2}}}, \:{{a_{2}}\ {b_{1}}}, \:{{{a_{1}}\ {b_{5}}}+{{a_{5}}\ {b_{1}}}}, \:{{a_{1}}\ {b_{3}}}, \:{{a_{2}}\ {b_{2}}}, \:{{a_{3}}\ {b_{1}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{1}}\ {b_{6}}}+{{a_{2}}\ {b_{5}}}}, \:{{{a_{5}}\ {b_{2}}}+{{a_{6}}\ {b_{1}}}}, \:{{{a_{5}}\ {b_{5}}}- 1}, \:{{{a_{1}}\ {b_{4}}}+{{a_{2}}\ {b_{3}}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{3}}\ {b_{2}}}+{{a_{4}}\ {b_{1}}}}, \:{{{a_{2}}\ {b_{6}}}+{{a_{3}}\ {b_{5}}}+ 1}, \:{{{a_{5}}\ {b_{3}}}+{{a_{6}}\ {b_{2}}}- 1}, \:{{a_{6}}\ {b_{5}}}, \: \right.
\
\
\displaystyle
\left.{{a_{5}}\ {b_{6}}}, \:{{{a_{2}}\ {b_{4}}}+{{a_{3}}\ {b_{3}}}+{{a_{4}}\ {b_{2}}}+ 1}, \:{{a_{4}}\ {b_{5}}}, \:{{a_{3}}\ {b_{6}}}, \:{{a_{6}}\ {b_{3}}}, \:{{a_{6}}\ {b_{6}}}, \: \right.
\
\
\displaystyle
\left.{{a_{5}}\ {b_{4}}}, \:{{a_{4}}\ {b_{3}}}, \:{{a_{4}}\ {b_{6}}}, \:{{a_{3}}\ {b_{4}}}, \:{{a_{6}}\ {b_{4}}}, \:{{a_{4}}\ {b_{4}}}\right]
\label{eq29}\begin{array}{@{}l}
\displaystyle
\left[{{a_{1}}\ {b_{1}}}, \:{{a_{1}}\ {b_{2}}}, \:{{a_{2}}\ {b_{1}}}, \:{{{a_{1}}\ {b_{5}}}+{{a_{5}}\ {b_{1}}}}, \:{{a_{1}}\ {b_{3}}}, \:{{a_{2}}\ {b_{2}}}, \:{{a_{3}}\ {b_{1}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{1}}\ {b_{6}}}+{{a_{2}}\ {b_{5}}}}, \:{{{a_{5}}\ {b_{2}}}+{{a_{6}}\ {b_{1}}}}, \:{{{a_{5}}\ {b_{5}}}- 1}, \:{{{a_{1}}\ {b_{4}}}+{{a_{2}}\ {b_{3}}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{3}}\ {b_{2}}}+{{a_{4}}\ {b_{1}}}}, \:{{{a_{2}}\ {b_{6}}}+{{a_{3}}\ {b_{5}}}+ 1}, \:{{{a_{5}}\ {b_{3}}}+{{a_{6}}\ {b_{2}}}- 1}, \:{{a_{6}}\ {b_{5}}}, \: \right.
\
\
\displaystyle
\left.{{a_{5}}\ {b_{6}}}, \:{{{a_{2}}\ {b_{4}}}+{{a_{3}}\ {b_{3}}}+{{a_{4}}\ {b_{2}}}+ 1}, \:{{a_{4}}\ {b_{5}}}, \:{{a_{3}}\ {b_{6}}}, \:{{a_{6}}\ {b_{3}}}, \:{{a_{6}}\ {b_{6}}}, \: \right.
\
\
\displaystyle
\left.{{a_{5}}\ {b_{4}}}, \:{{a_{4}}\ {b_{3}}}, \:{{a_{4}}\ {b_{6}}}, \:{{a_{3}}\ {b_{4}}}, \:{{a_{6}}\ {b_{4}}}, \:{{a_{4}}\ {b_{4}}}\right]](images/4075816841263113979-16.0px.png)
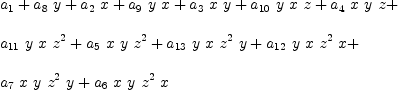
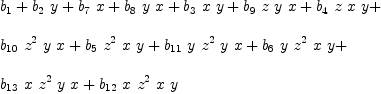
![\label{eq40}\begin{array}{@{}l}
\displaystyle
\left[{{a_{1}}\ {b_{1}}}, \:{{{a_{1}}\ {b_{2}}}+{{a_{8}}\ {b_{1}}}}, \:{{{a_{1}}\ {b_{7}}}+{{a_{2}}\ {b_{1}}}}, \:{{a_{8}}\ {b_{2}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{1}}\ {b_{8}}}+{{a_{8}}\ {b_{7}}}+{{a_{9}}\ {b_{1}}}}, \:{{{a_{1}}\ {b_{3}}}+{{a_{2}}\ {b_{2}}}+{{a_{3}}\ {b_{1}}}}, \:{{a_{2}}\ {b_{7}}}, \:{{a_{1}}\ {b_{9}}}, \: \right.
\
\
\displaystyle
\left.{{a_{1}}\ {b_{4}}}, \:{{a_{8}}\ {b_{8}}}, \:{{a_{10}}\ {b_{1}}}, \:{{{a_{8}}\ {b_{3}}}+{{a_{9}}\ {b_{2}}}}, \:{{a_{9}}\ {b_{7}}}, \:{{a_{4}}\ {b_{1}}}, \:{{a_{3}}\ {b_{2}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{2}}\ {b_{8}}}+{{a_{3}}\ {b_{7}}}}, \:{{a_{2}}\ {b_{3}}}, \:{{a_{1}}\ {b_{10}}}, \:{{a_{1}}\ {b_{5}}}, \:{{a_{8}}\ {b_{9}}}, \:{{a_{8}}\ {b_{4}}}, \:{{a_{11}}\ {b_{1}}}, \: \right.
\
\
\displaystyle
\left.{{a_{10}}\ {b_{2}}}, \:{{a_{10}}\ {b_{7}}}, \:{{a_{9}}\ {b_{8}}}, \:{{a_{9}}\ {b_{3}}}, \:{{a_{2}}\ {b_{9}}}, \:{{a_{2}}\ {b_{4}}}, \:{{a_{5}}\ {b_{1}}}, \:{{a_{4}}\ {b_{2}}}, \:{{a_{4}}\ {b_{7}}}, \: \right.
\
\
\displaystyle
\left.{{a_{3}}\ {b_{8}}}, \:{{a_{3}}\ {b_{3}}}, \:{{{a_{1}}\ {b_{11}}}+{{a_{8}}\ {b_{10}}}}, \:{{{a_{1}}\ {b_{6}}}+{{a_{8}}\ {b_{5}}}}, \:{{{a_{11}}\ {b_{2}}}+{{a_{13}}\ {b_{1}}}}, \right.
\
\
\displaystyle
\left.\:{{{a_{11}}\ {b_{7}}}+{{a_{12}}\ {b_{1}}}}, \:{{{a_{9}}\ {b_{9}}}+{{a_{10}}\ {b_{8}}}}, \:{{{a_{9}}\ {b_{4}}}+{{a_{10}}\ {b_{3}}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{1}}\ {b_{13}}}+{{a_{2}}\ {b_{10}}}}, \:{{{a_{1}}\ {b_{12}}}+{{a_{2}}\ {b_{5}}}}, \:{{{a_{5}}\ {b_{2}}}+{{a_{7}}\ {b_{1}}}}, \:{{{a_{5}}\ {b_{7}}}+{{a_{6}}\ {b_{1}}}}, \right.
\
\
\displaystyle
\left.\:{{{a_{3}}\ {b_{9}}}+{{a_{4}}\ {b_{8}}}}, \:{{{a_{3}}\ {b_{4}}}+{{a_{4}}\ {b_{3}}}}, \:{{a_{8}}\ {b_{11}}}, \:{{a_{8}}\ {b_{6}}}, \:{{a_{13}}\ {b_{2}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{8}}\ {b_{13}}}+{{a_{9}}\ {b_{10}}}+{{a_{10}}\ {b_{9}}}+{{a_{11}}\ {b_{8}}}+{{a_{13}}\ {b_{7}}}- 1}, \: \right.
\
\
\displaystyle
\left.{{{a_{8}}\ {b_{12}}}+{{a_{9}}\ {b_{5}}}+{{a_{10}}\ {b_{4}}}+{{a_{11}}\ {b_{3}}}+{{a_{12}}\ {b_{2}}}- 1}, \:{{a_{12}}\ {b_{7}}}, \:{{a_{7}}\ {b_{2}}}, \right.
\
\
\displaystyle
\left.\:{{{a_{2}}\ {b_{11}}}+{{a_{3}}\ {b_{10}}}+{{a_{4}}\ {b_{9}}}+{{a_{5}}\ {b_{8}}}+{{a_{7}}\ {b_{7}}}- 1}, \: \right.
\
\
\displaystyle
\left.{{{a_{2}}\ {b_{6}}}+{{a_{3}}\ {b_{5}}}+{{a_{4}}\ {b_{4}}}+{{a_{5}}\ {b_{3}}}+{{a_{6}}\ {b_{2}}}- 1}, \:{{a_{6}}\ {b_{7}}}, \:{{a_{2}}\ {b_{13}}}, \: \right.
\
\
\displaystyle
\left.{{a_{2}}\ {b_{12}}}, \:{{{a_{10}}\ {b_{10}}}+{{a_{11}}\ {b_{9}}}}, \:{{{a_{10}}\ {b_{5}}}+{{a_{11}}\ {b_{4}}}}, \:{{a_{1
3}}\ {b_{8}}}, \:{{a_{13}}\ {b_{3}}}, \: \right.
\
\
\displaystyle
\left.{{a_{12}}\ {b_{8}}}, \:{{a_{12}}\ {b_{3}}}, \:{{a_{9}}\ {b_{11}}}, \:{{a_{9}}\ {b_{6}}}, \:{{a_{9}}\ {b_{13}}}, \:{{a_{9}}\ {b_{12}}}, \:{{{a_{4}}\ {b_{10}}}+{{a_{5}}\ {b_{9}}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{4}}\ {b_{5}}}+{{a_{5}}\ {b_{4}}}}, \:{{a_{7}}\ {b_{8}}}, \:{{a_{7}}\ {b_{3}}}, \:{{a_{6}}\ {b_{8}}}, \:{{a_{6}}\ {b_{3}}}, \:{{a_{3}}\ {b_{11}}}, \:{{a_{3}}\ {b_{6}}}, \: \right.
\
\
\displaystyle
\left.{{a_{3}}\ {b_{13}}}, \:{{a_{3}}\ {b_{12}}}, \:{{a_{11}}\ {b_{10}}}, \:{{a_{11}}\ {b_{5}}}, \:{{a_{13}}\ {b_{9}}}, \:{{a_{1
3}}\ {b_{4}}}, \:{{a_{12}}\ {b_{9}}}, \: \right.
\
\
\displaystyle
\left.{{a_{12}}\ {b_{4}}}, \:{{a_{10}}\ {b_{11}}}, \:{{a_{10}}\ {b_{6}}}, \:{{a_{10}}\ {b_{13}}}, \:{{a_{10}}\ {b_{12}}}, \:{{a_{5}}\ {b_{10}}}, \:{{a_{5}}\ {b_{5}}}, \: \right.
\
\
\displaystyle
\left.{{a_{7}}\ {b_{9}}}, \:{{a_{7}}\ {b_{4}}}, \:{{a_{6}}\ {b_{9}}}, \:{{a_{6}}\ {b_{4}}}, \:{{a_{4}}\ {b_{11}}}, \:{{a_{4}}\ {b_{6}}}, \:{{a_{4}}\ {b_{13}}}, \:{{a_{4}}\ {b_{12}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{11}}\ {b_{11}}}+{{a_{13}}\ {b_{10}}}}, \:{{{a_{11}}\ {b_{6}}}+{{a_{13}}\ {b_{5}}}}, \:{{{a_{11}}\ {b_{13}}}+{{a_{12}}\ {b_{10}}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{11}}\ {b_{12}}}+{{a_{12}}\ {b_{5}}}}, \:{{{a_{5}}\ {b_{11}}}+{{a_{7}}\ {b_{10}}}}, \:{{{a_{5}}\ {b_{6}}}+{{a_{7}}\ {b_{5}}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{5}}\ {b_{13}}}+{{a_{6}}\ {b_{10}}}}, \:{{{a_{5}}\ {b_{12}}}+{{a_{6}}\ {b_{5}}}}, \:{{a_{13}}\ {b_{11}}}, \:{{a_{13}}\ {b_{6}}}, \:{{a_{13}}\ {b_{13}}}, \: \right.
\
\
\displaystyle
\left.{{a_{13}}\ {b_{12}}}, \:{{a_{12}}\ {b_{11}}}, \:{{a_{12}}\ {b_{6}}}, \:{{a_{12}}\ {b_{13}}}, \:{{a_{12}}\ {b_{12}}}, \:{{a_{7}}\ {b_{11}}}, \:{{a_{7}}\ {b_{6}}}, \: \right.
\
\
\displaystyle
\left.{{a_{7}}\ {b_{13}}}, \:{{a_{7}}\ {b_{12}}}, \:{{a_{6}}\ {b_{11}}}, \:{{a_{6}}\ {b_{6}}}, \:{{a_{6}}\ {b_{13}}}, \:{{a_{6}}\ {b_{12}}}\right]
\label{eq40}\begin{array}{@{}l}
\displaystyle
\left[{{a_{1}}\ {b_{1}}}, \:{{{a_{1}}\ {b_{2}}}+{{a_{8}}\ {b_{1}}}}, \:{{{a_{1}}\ {b_{7}}}+{{a_{2}}\ {b_{1}}}}, \:{{a_{8}}\ {b_{2}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{1}}\ {b_{8}}}+{{a_{8}}\ {b_{7}}}+{{a_{9}}\ {b_{1}}}}, \:{{{a_{1}}\ {b_{3}}}+{{a_{2}}\ {b_{2}}}+{{a_{3}}\ {b_{1}}}}, \:{{a_{2}}\ {b_{7}}}, \:{{a_{1}}\ {b_{9}}}, \: \right.
\
\
\displaystyle
\left.{{a_{1}}\ {b_{4}}}, \:{{a_{8}}\ {b_{8}}}, \:{{a_{10}}\ {b_{1}}}, \:{{{a_{8}}\ {b_{3}}}+{{a_{9}}\ {b_{2}}}}, \:{{a_{9}}\ {b_{7}}}, \:{{a_{4}}\ {b_{1}}}, \:{{a_{3}}\ {b_{2}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{2}}\ {b_{8}}}+{{a_{3}}\ {b_{7}}}}, \:{{a_{2}}\ {b_{3}}}, \:{{a_{1}}\ {b_{10}}}, \:{{a_{1}}\ {b_{5}}}, \:{{a_{8}}\ {b_{9}}}, \:{{a_{8}}\ {b_{4}}}, \:{{a_{11}}\ {b_{1}}}, \: \right.
\
\
\displaystyle
\left.{{a_{10}}\ {b_{2}}}, \:{{a_{10}}\ {b_{7}}}, \:{{a_{9}}\ {b_{8}}}, \:{{a_{9}}\ {b_{3}}}, \:{{a_{2}}\ {b_{9}}}, \:{{a_{2}}\ {b_{4}}}, \:{{a_{5}}\ {b_{1}}}, \:{{a_{4}}\ {b_{2}}}, \:{{a_{4}}\ {b_{7}}}, \: \right.
\
\
\displaystyle
\left.{{a_{3}}\ {b_{8}}}, \:{{a_{3}}\ {b_{3}}}, \:{{{a_{1}}\ {b_{11}}}+{{a_{8}}\ {b_{10}}}}, \:{{{a_{1}}\ {b_{6}}}+{{a_{8}}\ {b_{5}}}}, \:{{{a_{11}}\ {b_{2}}}+{{a_{13}}\ {b_{1}}}}, \right.
\
\
\displaystyle
\left.\:{{{a_{11}}\ {b_{7}}}+{{a_{12}}\ {b_{1}}}}, \:{{{a_{9}}\ {b_{9}}}+{{a_{10}}\ {b_{8}}}}, \:{{{a_{9}}\ {b_{4}}}+{{a_{10}}\ {b_{3}}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{1}}\ {b_{13}}}+{{a_{2}}\ {b_{10}}}}, \:{{{a_{1}}\ {b_{12}}}+{{a_{2}}\ {b_{5}}}}, \:{{{a_{5}}\ {b_{2}}}+{{a_{7}}\ {b_{1}}}}, \:{{{a_{5}}\ {b_{7}}}+{{a_{6}}\ {b_{1}}}}, \right.
\
\
\displaystyle
\left.\:{{{a_{3}}\ {b_{9}}}+{{a_{4}}\ {b_{8}}}}, \:{{{a_{3}}\ {b_{4}}}+{{a_{4}}\ {b_{3}}}}, \:{{a_{8}}\ {b_{11}}}, \:{{a_{8}}\ {b_{6}}}, \:{{a_{13}}\ {b_{2}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{8}}\ {b_{13}}}+{{a_{9}}\ {b_{10}}}+{{a_{10}}\ {b_{9}}}+{{a_{11}}\ {b_{8}}}+{{a_{13}}\ {b_{7}}}- 1}, \: \right.
\
\
\displaystyle
\left.{{{a_{8}}\ {b_{12}}}+{{a_{9}}\ {b_{5}}}+{{a_{10}}\ {b_{4}}}+{{a_{11}}\ {b_{3}}}+{{a_{12}}\ {b_{2}}}- 1}, \:{{a_{12}}\ {b_{7}}}, \:{{a_{7}}\ {b_{2}}}, \right.
\
\
\displaystyle
\left.\:{{{a_{2}}\ {b_{11}}}+{{a_{3}}\ {b_{10}}}+{{a_{4}}\ {b_{9}}}+{{a_{5}}\ {b_{8}}}+{{a_{7}}\ {b_{7}}}- 1}, \: \right.
\
\
\displaystyle
\left.{{{a_{2}}\ {b_{6}}}+{{a_{3}}\ {b_{5}}}+{{a_{4}}\ {b_{4}}}+{{a_{5}}\ {b_{3}}}+{{a_{6}}\ {b_{2}}}- 1}, \:{{a_{6}}\ {b_{7}}}, \:{{a_{2}}\ {b_{13}}}, \: \right.
\
\
\displaystyle
\left.{{a_{2}}\ {b_{12}}}, \:{{{a_{10}}\ {b_{10}}}+{{a_{11}}\ {b_{9}}}}, \:{{{a_{10}}\ {b_{5}}}+{{a_{11}}\ {b_{4}}}}, \:{{a_{1
3}}\ {b_{8}}}, \:{{a_{13}}\ {b_{3}}}, \: \right.
\
\
\displaystyle
\left.{{a_{12}}\ {b_{8}}}, \:{{a_{12}}\ {b_{3}}}, \:{{a_{9}}\ {b_{11}}}, \:{{a_{9}}\ {b_{6}}}, \:{{a_{9}}\ {b_{13}}}, \:{{a_{9}}\ {b_{12}}}, \:{{{a_{4}}\ {b_{10}}}+{{a_{5}}\ {b_{9}}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{4}}\ {b_{5}}}+{{a_{5}}\ {b_{4}}}}, \:{{a_{7}}\ {b_{8}}}, \:{{a_{7}}\ {b_{3}}}, \:{{a_{6}}\ {b_{8}}}, \:{{a_{6}}\ {b_{3}}}, \:{{a_{3}}\ {b_{11}}}, \:{{a_{3}}\ {b_{6}}}, \: \right.
\
\
\displaystyle
\left.{{a_{3}}\ {b_{13}}}, \:{{a_{3}}\ {b_{12}}}, \:{{a_{11}}\ {b_{10}}}, \:{{a_{11}}\ {b_{5}}}, \:{{a_{13}}\ {b_{9}}}, \:{{a_{1
3}}\ {b_{4}}}, \:{{a_{12}}\ {b_{9}}}, \: \right.
\
\
\displaystyle
\left.{{a_{12}}\ {b_{4}}}, \:{{a_{10}}\ {b_{11}}}, \:{{a_{10}}\ {b_{6}}}, \:{{a_{10}}\ {b_{13}}}, \:{{a_{10}}\ {b_{12}}}, \:{{a_{5}}\ {b_{10}}}, \:{{a_{5}}\ {b_{5}}}, \: \right.
\
\
\displaystyle
\left.{{a_{7}}\ {b_{9}}}, \:{{a_{7}}\ {b_{4}}}, \:{{a_{6}}\ {b_{9}}}, \:{{a_{6}}\ {b_{4}}}, \:{{a_{4}}\ {b_{11}}}, \:{{a_{4}}\ {b_{6}}}, \:{{a_{4}}\ {b_{13}}}, \:{{a_{4}}\ {b_{12}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{11}}\ {b_{11}}}+{{a_{13}}\ {b_{10}}}}, \:{{{a_{11}}\ {b_{6}}}+{{a_{13}}\ {b_{5}}}}, \:{{{a_{11}}\ {b_{13}}}+{{a_{12}}\ {b_{10}}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{11}}\ {b_{12}}}+{{a_{12}}\ {b_{5}}}}, \:{{{a_{5}}\ {b_{11}}}+{{a_{7}}\ {b_{10}}}}, \:{{{a_{5}}\ {b_{6}}}+{{a_{7}}\ {b_{5}}}}, \: \right.
\
\
\displaystyle
\left.{{{a_{5}}\ {b_{13}}}+{{a_{6}}\ {b_{10}}}}, \:{{{a_{5}}\ {b_{12}}}+{{a_{6}}\ {b_{5}}}}, \:{{a_{13}}\ {b_{11}}}, \:{{a_{13}}\ {b_{6}}}, \:{{a_{13}}\ {b_{13}}}, \: \right.
\
\
\displaystyle
\left.{{a_{13}}\ {b_{12}}}, \:{{a_{12}}\ {b_{11}}}, \:{{a_{12}}\ {b_{6}}}, \:{{a_{12}}\ {b_{13}}}, \:{{a_{12}}\ {b_{12}}}, \:{{a_{7}}\ {b_{11}}}, \:{{a_{7}}\ {b_{6}}}, \: \right.
\
\
\displaystyle
\left.{{a_{7}}\ {b_{13}}}, \:{{a_{7}}\ {b_{12}}}, \:{{a_{6}}\ {b_{11}}}, \:{{a_{6}}\ {b_{6}}}, \:{{a_{6}}\ {b_{13}}}, \:{{a_{6}}\ {b_{12}}}\right]](images/1513936853399017991-16.0px.png)