Solving Equations
What method is used to solve equation in Axiom?
fricas
(1) -> solve(sin(x)=4/5,x)
Type: List(Equation(Expression(Integer)))
fricas
solve([a=4,sin(x)=a/5],[a,x])
Type: List(List(Equation(Expression(Integer))))
In the following, a workaround is necessary because of bug #128:
fricas
)set output algebra on
fricas
)set output tex off
solve([V_q*U_q+V_l*U_l+V_d*U_d+V_a*U_a=U_ma, _
V_q*rho_q+V_l*rho_l+ V_d*rho_d+V_a*rho_a=rho_ma, _
V_q*t_q+V_l*t_l+V_d*t_d+V_a*t_a=t_ma, _
V_q+V_l+V_d+V_a=1], _
[V_q,V_l,V_d,V_a] )
(3)
[
[
V_q
=
((U_d - U_a)rho_l + (- U_l + U_a)rho_d + (U_l - U_d)rho_a)t_ma
+
((- U_d + U_a)rho_ma + (U_ma - U_a)rho_d + (- U_ma + U_d)rho_a)t_l
+
((U_l - U_a)rho_ma + (- U_ma + U_a)rho_l + (U_ma - U_l)rho_a)t_d
+
((- U_l + U_d)rho_ma + (U_ma - U_d)rho_l + (- U_ma + U_l)rho_d)t_a
/
((U_d - U_a)rho_l + (- U_l + U_a)rho_d + (U_l - U_d)rho_a)t_q
+
((- U_d + U_a)rho_q + (U_q - U_a)rho_d + (- U_q + U_d)rho_a)t_l
+
((U_l - U_a)rho_q + (- U_q + U_a)rho_l + (U_q - U_l)rho_a)t_d
+
((- U_l + U_d)rho_q + (U_q - U_d)rho_l + (- U_q + U_l)rho_d)t_a
,
V_l
=
((U_d - U_a)rho_ma + (- U_ma + U_a)rho_d + (U_ma - U_d)rho_a)t_q
+
((- U_d + U_a)rho_q + (U_q - U_a)rho_d + (- U_q + U_d)rho_a)t_ma
+
((U_ma - U_a)rho_q + (- U_q + U_a)rho_ma + (U_q - U_ma)rho_a)t_d
+
((- U_ma + U_d)rho_q + (U_q - U_d)rho_ma + (- U_q + U_ma)rho_d)t_a
/
((U_d - U_a)rho_l + (- U_l + U_a)rho_d + (U_l - U_d)rho_a)t_q
+
((- U_d + U_a)rho_q + (U_q - U_a)rho_d + (- U_q + U_d)rho_a)t_l
+
((U_l - U_a)rho_q + (- U_q + U_a)rho_l + (U_q - U_l)rho_a)t_d
+
((- U_l + U_d)rho_q + (U_q - U_d)rho_l + (- U_q + U_l)rho_d)t_a
,
V_d
=
((- U_l + U_a)rho_ma + (U_ma - U_a)rho_l + (- U_ma + U_l)rho_a)t_q
+
((U_l - U_a)rho_q + (- U_q + U_a)rho_l + (U_q - U_l)rho_a)t_ma
+
((- U_ma + U_a)rho_q + (U_q - U_a)rho_ma + (- U_q + U_ma)rho_a)t_l
+
((U_ma - U_l)rho_q + (- U_q + U_l)rho_ma + (U_q - U_ma)rho_l)t_a
/
((U_d - U_a)rho_l + (- U_l + U_a)rho_d + (U_l - U_d)rho_a)t_q
+
((- U_d + U_a)rho_q + (U_q - U_a)rho_d + (- U_q + U_d)rho_a)t_l
+
((U_l - U_a)rho_q + (- U_q + U_a)rho_l + (U_q - U_l)rho_a)t_d
+
((- U_l + U_d)rho_q + (U_q - U_d)rho_l + (- U_q + U_l)rho_d)t_a
,
V_a
=
((U_l - U_d)rho_ma + (- U_ma + U_d)rho_l + (U_ma - U_l)rho_d)t_q
+
((- U_l + U_d)rho_q + (U_q - U_d)rho_l + (- U_q + U_l)rho_d)t_ma
+
((U_ma - U_d)rho_q + (- U_q + U_d)rho_ma + (U_q - U_ma)rho_d)t_l
+
((- U_ma + U_l)rho_q + (U_q - U_l)rho_ma + (- U_q + U_ma)rho_l)t_d
/
((U_d - U_a)rho_l + (- U_l + U_a)rho_d + (U_l - U_d)rho_a)t_q
+
((- U_d + U_a)rho_q + (U_q - U_a)rho_d + (- U_q + U_d)rho_a)t_l
+
((U_l - U_a)rho_q + (- U_q + U_a)rho_l + (U_q - U_l)rho_a)t_d
+
((- U_l + U_d)rho_q + (U_q - U_d)rho_l + (- U_q + U_l)rho_d)t_a
]
]
Type: List(List(Equation(Fraction(Polynomial(Integer)))))
fricas
)set output algebra off
fricas
)set output tex on
fricas
solve(v^4+b*v^3+c*v^2+d=0,v)
Type: List(Equation(Fraction(Polynomial(Integer))))
This didn't work since solve returns solutions expressible as members of the
ground field only. Above, the ground field of 
defaults to
Fraction Polynomial Integer...
Thus, the proper call is
fricas
solve((v^4+b*v^3+c*v^2+d)::EXPR INT=0,v)
Type: List(Equation(Expression(Integer)))
But really, you should use 'zeroOf':
fricas
zeroOf(v^4+b*v^3+c*v^2+d, v)
Type: Expression(Integer)
In the following, we have to do three
things:
- convert the list of
Fraction Polynomial Float to a list of
Fraction Polynomial Integer, since solve can only handle the latter,
- ask for an approximate solution and
- set precision to a lower value then 68, since it would take too much time otherwise
Furthermore, it's %pi, not %PI.
Here is one way to use macros and _ to define more complex names that
print nicely in LaTeX form:
fricas
K_sc ==> K___{sc_}
Type: Void
fricas
mu_sc ==> _\mu___{sc_}
Type: Void
fricas
digits(7);
fricas
l:= [0.01*(2.25-K_sc)*K_sc/(0.01*%pi*mu_sc*(mu_sc+3.0*K_sc)/ _
(4.0*mu_sc+3.0*K_sc)+2.25)+0.7*(37.0-K_sc)*(4.0*mu_sc/3.0+K_sc)/ _
(4.0*mu_sc/3.0+37.0)+0.29*(2.25-K_sc)*(4.0*mu_sc/3.0+K_sc)/ _
(4.0*mu_sc/3.0+2.25), _
-0.002*mu_sc*(2.0*(2.0*mu_sc/3.0+2.25)/ _
(0.01*%pi*mu_sc*(mu_sc+3.0*K_sc)/ _
(4.0*mu_sc+3.0*K_sc)+2.25)+800.0*mu_sc/ _
(%pi*(2.0*mu_sc*(mu_sc+3.0*K_sc)/ _
(4.0*mu_sc+3.0*K_sc)+mu_sc))+1.0)+0.7*(44.0-mu_sc)*(mu_sc*(8.0*mu_sc+9.0*K_sc)/ _
(6.0*(2.0*mu_sc+K_sc))+mu_sc)/ _
(mu_sc*(8.0*mu_sc+9.0*K_sc)/ _
(6.0*(2.0*mu_sc+K_sc))+44.0)-1.74*(2.0*mu_sc+K_sc)*(mu_sc*(8.0*mu_sc+9.0*K_sc)/ _
(6.0*(2.0*mu_sc+K_sc))+mu_sc)/(8.0*mu_sc+9.0*K_sc)]
Type: List(Fraction(Polynomial(Float)))
fricas
-- solve exactly for fractions
a:=solve (l::LIST FRAC POLY FRAC INT::LIST FRAC POLY INT);
Type: List(List(Equation(Fraction(Polynomial(Integer)))))
fricas
-- Number of results:
#a
fricas
-- But only the first one is of interest.
-- Display it as a floating point result
a.1::List Equation Fraction POLY FLOAT
Type: List(Equation(Fraction(Polynomial(Float))))
fricas
-- Now check it
map(x+->subst(x,(a.1)::List Equation FRAC POLY FLOAT),l)
Type: List(Expression(Float))
fricas
)clear all
All user variables and function definitions have been cleared.
fricas
solve((x=-1+x^2)::EQ EXPR INT,x)
Type: List(Equation(Expression(Integer)))
quadratic equation
fricas
solve(a*x^2+b*x+c=0,x)
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
solve(a*x+b=0,x)
Type: List(Equation(Fraction(Polynomial(Integer))))
quadratic equation
fricas
solve(x^2+x-1,x)
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
radicalSolve(a*x^2+b*x+c=0,x)
Type: List(Equation(Expression(Integer)))
This doesn't work:
fricas
L := [ A = 2*P1+P2, B = 2*P2+P1, C = 2*Q1+Q2, D = 2*Q2+Q1]
Type: List(Equation(Polynomial(Integer)))
fricas
solve(L, [P1,P2])
Type: List(List(Equation(Fraction(Polynomial(Integer)))))
The reason is that above Q1 and Q2 are parameters. In such case FriCAS seeks
solution in rational functions of Q1 and Q2 and there is no such solution.
Instead one should solve also for Q1 and Q2:
fricas
)set output tex off
fricas
)set output algebra on
solve(L, [P1,P2,Q1,Q2])
- B + 2 A 2 B - A - D + 2 C 2 D - C
(8) [[P1 = ---------, P2 = -------, Q1 = ---------, Q2 = -------]]
3 3 3 3
Type: List(List(Equation(Fraction(Polynomial(Integer)))))
fricas
radicalSolve(a*x^3+b*x^2+c*x+d=0,x)
(9)
[
x
=
2 +---+ 2
(- 9 a \|- 3 + 9 a )
*
ROOT
+----------------------------------------------+
| 2 2 3 3 2 2
3 |27 a d + (- 18 a b c + 4 b )d + 4 a c - b c
54 a |----------------------------------------------
| 4
\| 108 a
+
2 3
- 27 a d + 9 a b c - 2 b
/
3
54 a
,
3
^
2
+
+---+
(- 3 a b\|- 3 - 3 a b)
*
ROOT
+----------------------------------------------+
| 2 2 3 3 2 2
3 |27 a d + (- 18 a b c + 4 b )d + 4 a c - b c
54 a |----------------------------------------------
| 4
\| 108 a
+
2 3
- 27 a d + 9 a b c - 2 b
/
3
54 a
,
3
+
2
6 a c - 2 b
/
2 +---+ 2
(9 a \|- 3 + 9 a )
*
ROOT
+----------------------------------------------+
| 2 2 3 3 2 2
3 |27 a d + (- 18 a b c + 4 b )d + 4 a c - b c
54 a |----------------------------------------------
| 4
\| 108 a
+
2 3
- 27 a d + 9 a b c - 2 b
/
3
54 a
,
3
,
x
=
2 +---+ 2
(- 9 a \|- 3 - 9 a )
*
ROOT
+----------------------------------------------+
| 2 2 3 3 2 2
3 |27 a d + (- 18 a b c + 4 b )d + 4 a c - b c
54 a |----------------------------------------------
| 4
\| 108 a
+
2 3
- 27 a d + 9 a b c - 2 b
/
3
54 a
,
3
^
2
+
+---+
(- 3 a b\|- 3 + 3 a b)
*
ROOT
+----------------------------------------------+
| 2 2 3 3 2 2
3 |27 a d + (- 18 a b c + 4 b )d + 4 a c - b c
54 a |----------------------------------------------
| 4
\| 108 a
+
2 3
- 27 a d + 9 a b c - 2 b
/
3
54 a
,
3
+
2
- 6 a c + 2 b
/
2 +---+ 2
(9 a \|- 3 - 9 a )
*
ROOT
+----------------------------------------------+
| 2 2 3 3 2 2
3 |27 a d + (- 18 a b c + 4 b )d + 4 a c - b c
54 a |----------------------------------------------
| 4
\| 108 a
+
2 3
- 27 a d + 9 a b c - 2 b
/
3
54 a
,
3
,
x
=
2
9 a
*
ROOT
+----------------------------------------------+
| 2 2 3 3 2 2
3 |27 a d + (- 18 a b c + 4 b )d + 4 a c - b c
54 a |----------------------------------------------
| 4
\| 108 a
+
2 3
- 27 a d + 9 a b c - 2 b
/
3
54 a
,
3
^
2
+
-
3 a b
*
ROOT
+----------------------------------------------+
| 2 2 3 3 2 2
3 |27 a d + (- 18 a b c + 4 b )d + 4 a c - b c
54 a |----------------------------------------------
| 4
\| 108 a
+
2 3
- 27 a d + 9 a b c - 2 b
/
3
54 a
,
3
+
2
- 3 a c + b
/
2
9 a
*
ROOT
+----------------------------------------------+
| 2 2 3 3 2 2
3 |27 a d + (- 18 a b c + 4 b )d + 4 a c - b c
54 a |----------------------------------------------
| 4
\| 108 a
+
2 3
- 27 a d + 9 a b c - 2 b
/
3
54 a
,
3
]
Type: List(Equation(Expression(Integer)))
fricas
)set output algebra off
fricas
)set output tex on
fricas
solve(x^2=y,x)
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
solve(x3=x0+(x1-x0)*t + (x2-x0) *u,u)
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
solve([x+y=3,x-y=1],[x,y])
Type: List(List(Equation(Fraction(Polynomial(Integer)))))
An error in the way
MathAction folds the
LaTeX output from
Axiom prevents this expression from displaying properly. As
a work-a-round it is necessary to disable the
LaTeX output
and replace it with a ASCII text equivalent.
fricas
)set output tex off
fricas
)set output algebra on
A:=i=(a*x+c*z+e)/(z+g)
c z + a x + e
(13) i = -------------
z + g
Type: Equation(Fraction(Polynomial(Integer)))
fricas
B:=j=(b*x+d*z+f)/(z+g)
d z + b x + f
(14) j = -------------
z + g
Type: Equation(Fraction(Polynomial(Integer)))
fricas
solve([A,B],[x,z])
(15)
(c g - e)j + (- d g + f)i - c f + d e - a g j + b g i + a f - b e
[[x = -------------------------------------, z = ---------------------------]
a j - b i - a d + b c a j - b i - a d + b c
]
Type: List(List(Equation(Fraction(Polynomial(Integer)))))
fricas
)set output tex on
fricas
)set output algebra off
fricas
solve(14=x*1.1^x,x)
There are 20 exposed and 3 unexposed library operations named solve
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op solve
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named solve
with argument type(s)
Equation(Expression(Float))
Variable(x)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
fricas
)set output algebra on
fricas
)set output tex off
zerosOf((1-a)*x^4+x^3+x^2+x+1,x)
(16)
[%x6, %x7,
-
ROOT
2 2 2
(- 3 a + 6 a - 3)%x7 + ((- 2 a + 4 a - 2)%x6 + 2 a - 2)%x7
+
2 2
(- 3 a + 6 a - 3)%x6 + (2 a - 2)%x6 + 4 a - 3
+
(- a + 1)%x7 + (- a + 1)%x6 + 1
/
2 a - 2
,
ROOT
2 2 2
(- 3 a + 6 a - 3)%x7 + ((- 2 a + 4 a - 2)%x6 + 2 a - 2)%x7
+
2 2
(- 3 a + 6 a - 3)%x6 + (2 a - 2)%x6 + 4 a - 3
+
(- a + 1)%x7 + (- a + 1)%x6 + 1
/
2 a - 2
]
Type: List(Expression(Integer))
fricas
)set output algebra off
fricas
)set output tex on
fricas
solve( dx_p = ( m / b ) * ( c0 - b * dv_p + c0 * log(c0) - _
c0 * log( c0 - b * dv_p ) + v0 * log(c0) - _
v0 * log( c0 - b * dv_p ) - ( c0 / b ) ), dv_p )
Type: List(Equation(Expression(Integer)))
fricas
solve(((1+sqrt(5))^n-(1-sqrt(5))^n)/(sqrt(5)*2^n)=10^1001, n)
Type: List(Equation(Expression(Integer)))
fricas
)set output tex off
fricas
)set output algebra on
fricas
solve([nnH+2*niH+nnCs+2*niCs = n, (niH+niCs)*niH/nnH = SH, (niH+niCs)*niCs/nnCs = SCs, (niH+nnH)/(niCs+nnCs) = alpha],[nnH, niH, nnCs, niCs])
(19)
[
[
nnH
=
2 2
((- 2 SH + 2 SCs)alpha + (- 3 SH + 3 SCs)alpha - SH + SCs)niCs
+
2
(- 2 SH alpha + (- SH - SCs)alpha)n
+
2 2 2
(- 4 SCs SH + 2 SCs )alpha + (- 6 SCs SH + 4 SCs )alpha
+
2
- 2 SCs SH + 2 SCs
*
niCs
+
2 2 2
SCs alpha n + ((2 SCs SH - SCs )alpha + SCs SH - SCs )n
/
2 2
(SCs alpha + SCs)n + SCs alpha + SCs
,
niH
=
2
((SH - SCs)alpha + SH - SCs)niCs
+
2 2
(SH alpha n + (2 SCs SH - SCs )alpha + 2 SCs SH - 2 SCs )niCs
+
2
(- SCs SH + SCs )n
/
2
SCs n + SCs
,
nnCs
=
2
((- SH + SCs)alpha - SH + SCs)niCs
+
(((- SH - SCs)alpha - 2 SCs)n - 2 SCs SH alpha - 2 SCs SH)niCs
+
2
SCs n + SCs SH n
/
2 2
(SCs alpha + SCs)n + SCs alpha + SCs
,
2 3
((SH - SCs)alpha + (2 SH - 2 SCs)alpha + SH - SCs)niCs
+
2 2 2
(SH alpha + (SH + SCs)alpha + SCs)n + (2 SCs SH - SCs )alpha
+
2 2
(5 SCs SH - 3 SCs )alpha + 3 SCs SH - 2 SCs
*
2
niCs
+
2 2 2 2
((2 SCs alpha - SCs SH + 3 SCs )n + 2 SCs SH alpha + 2 SCs SH)niCs
+
2 2 2
- SCs n - SCs SH n
=
0
]
]
Type: List(List(Equation(Fraction(Polynomial(Integer)))))
fricas
solve((-v^3 * cos(x) * sin(x)^2 / sqrt(v^2 * cos(x)^2 + 2*a*h) - v^2 * sin(x)^2 + v * cos(x) * sqrt(v^2 * cos(x)^2 + 2 * a * h) + v^2 * cos(x)^2)) / a
>> Error detected within library code:
too many variables
![\label{eq1}\left[{x ={\arcsin \left({\frac{4}{5}}\right)}}\right]](images/2835323481703177854-16.0px.png "\label{eq1}\left[{x ={\arcsin \left({\frac{4}{5}}\right)}}\right]")
![\label{eq2}\left[ \right]](images/4639340934722937175-16.0px.png "\label{eq2}\left[ \right]")
![\label{eq3}\left[{{{{v}^{4}}+{b \ {{v}^{3}}}+{c \ {{v}^{2}}}+ d}= 0}\right]](images/5413503641855554152-16.0px.png "\label{eq3}\left[{{{{v}^{4}}+{b \ {{v}^{3}}}+{c \ {{v}^{2}}}+ d}= 0}\right]")
![\label{eq4}\begin{array}{@{}l}
\displaystyle
\left[{v = \%v 0}, \:{v = \%v 1}, \: \right.
\
\
\displaystyle
\left.{
\begin{array}{@{}l}
\displaystyle
v =
\
\
\displaystyle
{\frac{{\sqrt{-{3 \ {{\%v 1}^{2}}}+{{\left(-{2 \ \%v 0}-{2 \ b}\right)}\ \%v 1}-{3 \ {{\%v 0}^{2}}}-{2 \ b \ \%v 0}-{4 \ c}+{{b}^{2}}}}- \%v 1 - \%v 0 - b}{2}}](images/2562873278686680464-16.0px.png "\label{eq4}\begin{array}{@{}l}
\displaystyle
\left[{v = \%v 0}, \:{v = \%v 1}, \: \right.
\
\
\displaystyle
\left.{
\begin{array}{@{}l}
\displaystyle
v =
\
\
\displaystyle
{\frac{{\sqrt{-{3 \ {{\%v 1}^{2}}}+{{\left(-{2 \ \%v 0}-{2 \ b}\right)}\ \%v 1}-{3 \ {{\%v 0}^{2}}}-{2 \ b \ \%v 0}-{4 \ c}+{{b}^{2}}}}- \%v 1 - \%v 0 - b}{2}}")
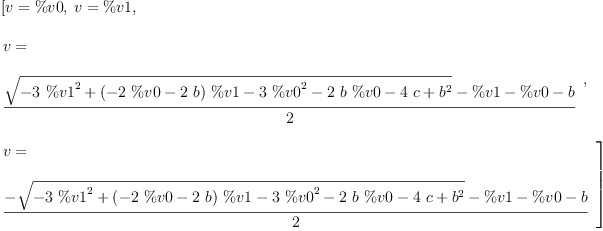
![\label{eq6}\begin{array}{@{}l}
\displaystyle
\left[{\frac{{{\left(-{{0.99}\ K \_{sc}}+{26.5525}\right)}\ {{\mu \_{sc}}^{4}}}+{{\left(-{{4.98574}\ {{K \_{sc}}^{2}}}-{{190.40
62}\ K \_{sc}}+{7668.544}\right)}\ {{\mu \_{sc}}^{3}}}+{{\left(-{{3.18243}\ {{K \_{sc}}^{3}}}-{{435.6183}\ {{K \_{sc}}^{2}}}+{{9082.386}\ K \_{sc}}+{17708.16}\right)}\ {{\mu \_{sc}}^{2}}}+{{\left(-{{208.4084}\ {{K \_{sc}}^{3}}}+{{455.729}\ {{K \_{sc}}^{2}}}+{{26696.39}\ K \_{sc}}\right)}\ \mu \_{sc}}-{{1531.87
9}\ {{K \_{sc}}^{3}}}+{{10061.45}\ {{K \_{sc}}^{2}}}}{{{\mu \_{sc}}^{4}}+{{\left({{3.0}\ K \_{sc}}+{315.9164}\right)}\ {{\mu \_{sc}}^{3}}}+{{\left({{303.1717}\ K \_{sc}}+{8480.051}\right)}\ {{\mu \_{sc}}^{2}}}+{{\left({{6465.401}\ K \_{sc}}+{13415.27}\right)}\ \mu \_{sc}}+{{10061.45}\ K \_{sc}}}}, \right.
\
\
\displaystyle
\left.\: \right.
\
\
\displaystyle
\left.{\frac{-{{3.156061}\ {{\mu \_{sc}}^{7}}}+{{\left(-{{19.3
567}\ K \_{sc}}-{823.8225}\right)}\ {{\mu \_{sc}}^{6}}}+{{\left(-{{40.72939}\ {{K \_{sc}}^{2}}}-{{3289.616}\ K \_{sc}}+{1817.7}\right)}\ {{\mu \_{sc}}^{5}}}+{{\left(-{{35.46834}\ {{K \_{sc}}^{3}}}-{{4668.2
97}\ {{K \_{sc}}^{2}}}+{{22513.6}\ K \_{sc}}\right)}\ {{\mu \_{sc}}^{4}}}+{{\left(-{{10.85896}\ {{K \_{sc}}^{4}}}-{{2766.3
75}\ {{K \_{sc}}^{3}}}+{{53897.04}\ {{K \_{sc}}^{2}}}\right)}\ {{\mu \_{sc}}^{3}}}+{{\left(-{{575.9874}\ {{K \_{sc}}^{4}}}+{{45929.1
9}\ {{K \_{sc}}^{3}}}\right)}\ {{\mu \_{sc}}^{2}}}+{{13052.6}\ {{K \_{sc}}^{4}}\ \mu \_{sc}}}{{{\mu \_{sc}}^{6}}+{{\left({{6.75}\ K \_{sc}}+{352.4789}\right)}\ {{\mu \_{sc}}^{5}}}+{{\left({{1
5.89063}\ {{K \_{sc}}^{2}}}+{{1693.405}\ K \_{sc}}+{18907.61}\right)}\ {{\mu \_{sc}}^{4}}}+{{\left({{15.82031}\ {{K \_{sc}}^{3}}}+{{2951.9
13}\ {{K \_{sc}}^{2}}}+{{73266.98}\ K \_{sc}}\right)}\ {{\mu \_{sc}}^{3}}}+{{\left({{5.695313}\ {{K \_{sc}}^{4}}}+{{2190.6
31}\ {{K \_{sc}}^{3}}}+{{101037.5}\ {{K \_{sc}}^{2}}}\right)}\ {{\mu \_{sc}}^{2}}}+{{\left({{574.9593}\ {{K \_{sc}}^{4}}}+{{58495.4
1}\ {{K \_{sc}}^{3}}}\right)}\ \mu \_{sc}}+{{11964.97}\ {{K \_{sc}}^{4}}}}}\right]](images/9026079232315422064-16.0px.png "\label{eq6}\begin{array}{@{}l}
\displaystyle
\left[{\frac{{{\left(-{{0.99}\ K \_{sc}}+{26.5525}\right)}\ {{\mu \_{sc}}^{4}}}+{{\left(-{{4.98574}\ {{K \_{sc}}^{2}}}-{{190.40
62}\ K \_{sc}}+{7668.544}\right)}\ {{\mu \_{sc}}^{3}}}+{{\left(-{{3.18243}\ {{K \_{sc}}^{3}}}-{{435.6183}\ {{K \_{sc}}^{2}}}+{{9082.386}\ K \_{sc}}+{17708.16}\right)}\ {{\mu \_{sc}}^{2}}}+{{\left(-{{208.4084}\ {{K \_{sc}}^{3}}}+{{455.729}\ {{K \_{sc}}^{2}}}+{{26696.39}\ K \_{sc}}\right)}\ \mu \_{sc}}-{{1531.87
9}\ {{K \_{sc}}^{3}}}+{{10061.45}\ {{K \_{sc}}^{2}}}}{{{\mu \_{sc}}^{4}}+{{\left({{3.0}\ K \_{sc}}+{315.9164}\right)}\ {{\mu \_{sc}}^{3}}}+{{\left({{303.1717}\ K \_{sc}}+{8480.051}\right)}\ {{\mu \_{sc}}^{2}}}+{{\left({{6465.401}\ K \_{sc}}+{13415.27}\right)}\ \mu \_{sc}}+{{10061.45}\ K \_{sc}}}}, \right.
\
\
\displaystyle
\left.\: \right.
\
\
\displaystyle
\left.{\frac{-{{3.156061}\ {{\mu \_{sc}}^{7}}}+{{\left(-{{19.3
567}\ K \_{sc}}-{823.8225}\right)}\ {{\mu \_{sc}}^{6}}}+{{\left(-{{40.72939}\ {{K \_{sc}}^{2}}}-{{3289.616}\ K \_{sc}}+{1817.7}\right)}\ {{\mu \_{sc}}^{5}}}+{{\left(-{{35.46834}\ {{K \_{sc}}^{3}}}-{{4668.2
97}\ {{K \_{sc}}^{2}}}+{{22513.6}\ K \_{sc}}\right)}\ {{\mu \_{sc}}^{4}}}+{{\left(-{{10.85896}\ {{K \_{sc}}^{4}}}-{{2766.3
75}\ {{K \_{sc}}^{3}}}+{{53897.04}\ {{K \_{sc}}^{2}}}\right)}\ {{\mu \_{sc}}^{3}}}+{{\left(-{{575.9874}\ {{K \_{sc}}^{4}}}+{{45929.1
9}\ {{K \_{sc}}^{3}}}\right)}\ {{\mu \_{sc}}^{2}}}+{{13052.6}\ {{K \_{sc}}^{4}}\ \mu \_{sc}}}{{{\mu \_{sc}}^{6}}+{{\left({{6.75}\ K \_{sc}}+{352.4789}\right)}\ {{\mu \_{sc}}^{5}}}+{{\left({{1
5.89063}\ {{K \_{sc}}^{2}}}+{{1693.405}\ K \_{sc}}+{18907.61}\right)}\ {{\mu \_{sc}}^{4}}}+{{\left({{15.82031}\ {{K \_{sc}}^{3}}}+{{2951.9
13}\ {{K \_{sc}}^{2}}}+{{73266.98}\ K \_{sc}}\right)}\ {{\mu \_{sc}}^{3}}}+{{\left({{5.695313}\ {{K \_{sc}}^{4}}}+{{2190.6
31}\ {{K \_{sc}}^{3}}}+{{101037.5}\ {{K \_{sc}}^{2}}}\right)}\ {{\mu \_{sc}}^{2}}}+{{\left({{574.9593}\ {{K \_{sc}}^{4}}}+{{58495.4
1}\ {{K \_{sc}}^{3}}}\right)}\ \mu \_{sc}}+{{11964.97}\ {{K \_{sc}}^{4}}}}}\right]")
![\label{eq8}\left[{\mu \_{sc}={0.0}}, \:{K \_{sc}={6.568047}}\right]](images/3895232874710484904-16.0px.png "\label{eq8}\left[{\mu \_{sc}={0.0}}, \:{K \_{sc}={6.568047}}\right]")
![\label{eq9}\left[{0.0}, \:{0.0}\right]](images/7777694375848649443-16.0px.png "\label{eq9}\left[{0.0}, \:{0.0}\right]")
![\label{eq10}\left[{x ={\frac{{\sqrt{5}}+ 1}{2}}}, \:{x ={\frac{-{\sqrt{5}}+ 1}{2}}}\right]](images/3735695839723513692-16.0px.png "\label{eq10}\left[{x ={\frac{{\sqrt{5}}+ 1}{2}}}, \:{x ={\frac{-{\sqrt{5}}+ 1}{2}}}\right]")
![\label{eq11}\left[{{{a \ {{x}^{2}}}+{b \ x}+ c}= 0}\right]](images/4311196400694307604-16.0px.png "\label{eq11}\left[{{{a \ {{x}^{2}}}+{b \ x}+ c}= 0}\right]")
![\label{eq12}\left[{x = -{\frac{b}{a}}}\right]](images/537194817202715371-16.0px.png "\label{eq12}\left[{x = -{\frac{b}{a}}}\right]")
![\label{eq13}\left[{{{{x}^{2}}+ x - 1}= 0}\right]](images/2308963947823185382-16.0px.png "\label{eq13}\left[{{{{x}^{2}}+ x - 1}= 0}\right]")
![\label{eq14}\begin{array}{@{}l}
\displaystyle
\left[{x ={\frac{-{\sqrt{-{4 \ a \ c}+{{b}^{2}}}}- b}{2 \ a}}}, \: \right.
\
\
\displaystyle
\left.{x ={\frac{{\sqrt{-{4 \ a \ c}+{{b}^{2}}}}- b}{2 \ a}}}\right]](images/1811132579062576311-16.0px.png "\label{eq14}\begin{array}{@{}l}
\displaystyle
\left[{x ={\frac{-{\sqrt{-{4 \ a \ c}+{{b}^{2}}}}- b}{2 \ a}}}, \: \right.
\
\
\displaystyle
\left.{x ={\frac{{\sqrt{-{4 \ a \ c}+{{b}^{2}}}}- b}{2 \ a}}}\right]")
![\label{eq15}\begin{array}{@{}l}
\displaystyle
\left[{A ={P 2 +{2 \ P 1}}}, \:{B ={{2 \ P 2}+ P 1}}, \:{C ={Q 2 +{2 \ Q 1}}}, \: \right.
\
\
\displaystyle
\left.{D ={{2 \ Q 2}+ Q 1}}\right]](images/7670241622770146677-16.0px.png "\label{eq15}\begin{array}{@{}l}
\displaystyle
\left[{A ={P 2 +{2 \ P 1}}}, \:{B ={{2 \ P 2}+ P 1}}, \:{C ={Q 2 +{2 \ Q 1}}}, \: \right.
\
\
\displaystyle
\left.{D ={{2 \ Q 2}+ Q 1}}\right]")
![\label{eq16}\left[ \right]](images/3763945104387423615-16.0px.png "\label{eq16}\left[ \right]")
![\label{eq17}\left[{{y -{{x}^{2}}}= 0}\right]](images/6626725044909927963-16.0px.png "\label{eq17}\left[{{y -{{x}^{2}}}= 0}\right]")
![\label{eq18}\left[{u ={\frac{x 3 -{t \ x 1}+{{\left(t - 1 \right)}\ x 0}}{x 2 - x 0}}}\right]](images/5691519487523357299-16.0px.png "\label{eq18}\left[{u ={\frac{x 3 -{t \ x 1}+{{\left(t - 1 \right)}\ x 0}}{x 2 - x 0}}}\right]")
![\label{eq19}\left[{\left[{x = 2}, \:{y = 1}\right]}\right]](images/3383396533935064483-16.0px.png "\label{eq19}\left[{\left[{x = 2}, \:{y = 1}\right]}\right]")
![\label{eq20}\left[ \right]](images/6065393688934802760-16.0px.png "\label{eq20}\left[ \right]")
![\label{eq21}\left[ \right]](images/8188311882178940711-16.0px.png "\label{eq21}\left[ \right]")