|
|
|
last edited 12 years ago by test1 |
Edit detail for SandBoxCliffordAlgebra revision 9 of 9
| 1 2 3 4 5 6 7 8 9 | ||
|
Editor: test1
Time: 2013/07/31 14:43:30 GMT+0 |
||
| Note: | ||
changed: -We want to test some properties of the CliffordAlgebra domain implemented in AXIOM(TM) We want to test some properties of the CliffordAlgebra domain implemented in FriCAS
We want to test some properties of the CliffordAlgebra? domain implemented in FriCAS
fricas
(1) -> diagMat:=matrix[[1,0, 0], [0, 1, 0], [0, 0, 1]]
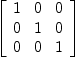 | (1) |
Type: Matrix(NonNegativeInteger?)
fricas
CLDQ := CliffordAlgebra(3,Fraction(Integer), diagMat)
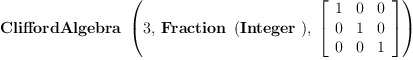 | (2) |
Type: Type
CLDQ contains now the Clifford algebra constructor for the Clifford algebra CL(R^3,Q) corresponding to the diagonal quadratic form in the basis of generators ei=e(i)
fricas
basGen: List CLDQ :=[1,e(1), e(2), e(1)*e(2), e(3), e(1)*e(3), e(2)*e(3), e(1)*e(2)*e(3)]
| (3) |
And we can now compute within this basis
fricas
elem1: CLDQ :=2*e(1)+e(2)
| (4) |
fricas
elem2: CLDQ :=1/2+e(2)+3*e(1)*e(3)
| (5) |
fricas
elem1*elem2
| (6) |
which is fine.
Lets now see what happens if we change the basis. We define new generators
fricas
f1:CLDQ := e(1)-e(2)
| (7) |
fricas
f2:CLDQ := e(2)-e(3)
| (8) |
fricas
f3:CLDQ := e(1)+e(2)+e(3)
| (9) |
fricas
lstFGen: List CLDQ := [f1,f2, f3]
| (10) |
and check what the new defining relations are
fricas
matrix [[y*x for x in lstFGen] for y in lstFGen]
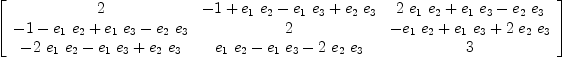 | (11) |
However, let us do the same calculations with another, symmetric but not diagonal quadratic form
fricas
offDiagMat:=matrix[[0,0, 1], [0, 1, 0], [1, 0, 0]]
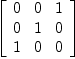 | (12) |
Type: Matrix(NonNegativeInteger?)
fricas
CLODQ := CliffordAlgebra(3,Fraction(Integer), offDiagMat)
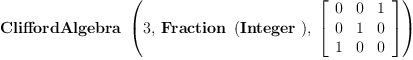 | (13) |
Type: Type
fricas
basGenO: List CLODQ :=[1,e(1), e(2), e(1)*e(2), e(3), e(1)*e(3), e(2)*e(3), e(1)*e(2)*e(3)]
| (14) |
fricas
basO: List CLODQ :=[e(1),e(2), e(3)]
| (15) |
and let us check the multiplication table on the basis and in general:
fricas
matrix [[y*x for x in basO] for y in basO]
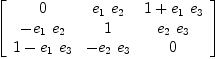 | (16) |
fricas
matrix [[y*x for x in basGenO] for y in basGenO]
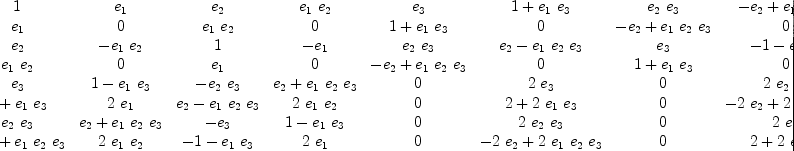 | (17) |
Note: Before Martin Baker fixed CliffordAlgebra? the results with off diagonal form were wrong.