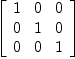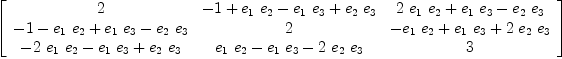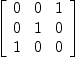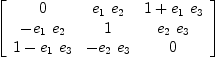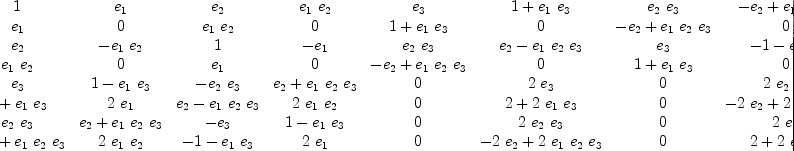We want to test some properties of the CliffordAlgebra? domain implemented in FriCAS fricas (1) -> diagMat:=matrix[[1,
Type: Matrix(NonNegativeInteger?)
fricas CLDQ := CliffordAlgebra(3,
Type: Type
CLDQ contains now the Clifford algebra constructor for the Clifford algebra CL(R^3,Q) corresponding to the diagonal quadratic form in the basis of generators ei=e(i) fricas basGen: List CLDQ :=[1,
And we can now compute within this basis fricas elem1: CLDQ :=2*e(1)+e(2)
fricas elem2: CLDQ :=1/2+e(2)+3*e(1)*e(3)
fricas elem1*elem2
which is fine. Lets now see what happens if we change the basis. We define new generators fricas f1:CLDQ := e(1)-e(2)
fricas f2:CLDQ := e(2)-e(3)
fricas f3:CLDQ := e(1)+e(2)+e(3)
fricas lstFGen: List CLDQ := [f1,
and check what the new defining relations are fricas matrix [[y*x for x in lstFGen] for y in lstFGen]
However, let us do the same calculations with another, symmetric but not diagonal quadratic form fricas offDiagMat:=matrix[[0,
Type: Matrix(NonNegativeInteger?)
fricas CLODQ := CliffordAlgebra(3,
Type: Type
fricas basGenO: List CLODQ :=[1,
fricas basO: List CLODQ :=[e(1),
and let us check the multiplication table on the basis and in general: fricas matrix [[y*x for x in basO] for y in basO]
fricas matrix [[y*x for x in basGenO] for y in basGenO]
Note: Before Martin Baker fixed CliffordAlgebra? the results with off diagonal form were wrong. |
|
|
|
last edited 12 years ago by test1 |