|
|
|
last edited 4 months ago by test1 |
Edit detail for Symbolic Integration revision 16 of 16
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 | ||
|
Editor: test1
Time: 2025/07/23 14:26:04 GMT+0 |
||
| Note: | ||
changed: -Unfortunately, due to a bug during final processing this result got mangled and elliptic -integral part is dropped, giving wrong result. - -We gets correct result when we keep only algebraic part Below is result when we keep only algebraic part
Errors in symbolic integration
Risch-Bronstein-Trager algorithm (Risch algorithm in short) is a complete algorithm for integration in terms of elementary functions. The algorithm either finds elementary integral or proves that there is none. Existence of elementary integral is relatively rare, so given random elementary function probably does not have elementary integral. FriCAS implementation of Risch algorithm is probably the "most complete" existing implementation. Unfortunately "most complete" does not mean complete, some parts are still unimplemented. See RischImplementationStatus. Unlike some other systems FriCAS will not give you unevaluated result when hitting unimplemented part. Instead, it signals error with message indicating that given integral requires unimplemented part. So when FriCAS returns unevaluated result almost surely there is no elementary integral. Almost surely, because as all programs FriCAS may have bugs...
FriCAS in fact implements extension of Risch algorithm which extends class of integrands
to some Liouvillian functions and for integration in terms of Ei, Ci, Si, li, erf,
fresnelS, fresnelC, incomplete Gamma, polylogs and elliptic integrals. There is complete
extended algorithm for large class of functions. However polylog and elliptic integrals cause
tricky theoretical problems. Compared to
theory current FriCAS implementation
contains considerable gaps. Nevertheless, FriCAS can handle a lot of examples
involving special functions that no other system can handle.
- FriCAS used to contain relatively weak pattern matching integrator capable of generating a few special functions
- Ei, li, dilog
and erf. Currently pattern matching is only used for one case of definite integration, all indefinite
integrals are done by Risch algorithm or extentions and shortcuts.
FriCAS Examples
1)
(1) -> integrate(sin(x)+sqrt(1-x^3),x)
| (1) |
Here FriCAS proved that result is not elementary and found integral in terms of elliptic functions.
Below is result when we keep only algebraic part
integrate(sqrt(1-x^3),x)
| (2) |
Reduce code
int(sin(x)+sqrt(1-x^3),x); | reduce |
2)
integrate(sqrt(1-log(sin(x)^2)),x)
>> Error detected within library code: integrate: implementation incomplete (constant residues)
In this case FriCAS neither can compute elementary result nor can it prove that result is not elementary, so it gives up with error message indicating that the handling this integral requires unimplemented part of Bronstein-Trager algorithm.
Reduce answer:
int(sqrt(1-log(sin(x)^2)),x); | reduce |
3)
integrate(sqrt(sin(1/x)),x)
>> Error detected within library code: integrate: implementation incomplete (has polynomial part)
Again, this integral needs unimplemented part of Bronstein-Trager algorithm.
Reduce reduce answer:
int(sqrt(sin(1/x)),x); | reduce |
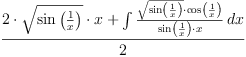 |
4)
)set output tex off
)set output algebra on
integrate(sqrt(sin(x)),x)
(3) +------+ | +---+ |\|- 1 |------ \| 2 * weierstrassZeta 4 ,0 , +---+ +---+ - sin(x) + \|- 1 cos(x) + \|- 1 weierstrassPInverse(4, 0, --------------------------------) +---+ +---+ sin(x) + \|- 1 cos(x) + \|- 1 + +--------+ | +---+ | \|- 1 |- ------ \| 2 * weierstrassZeta 4 , 0 , +---+ +---+ - sin(x) - \|- 1 cos(x) - \|- 1 weierstrassPInverse(4, 0, --------------------------------) +---+ +---+ sin(x) - \|- 1 cos(x) - \|- 1 / +--------+ +------+ | +---+ | +---+ | \|- 1 |\|- 1 |- ------ |------ \| 2 \| 2
This time FriCAS can prove that result is nonelementary and returns answer in terms of elliptic functions.
Reduce answer:
int(sqrt(sin(x)),x); | reduce |
For this Maple 9 gives the following result:
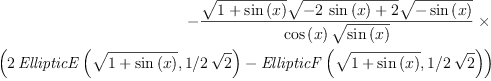 | (3) |
And Mathematica 4 gives:
| (4) |
- symbolic integration
- Tue, 22 Mar 2005 11:48:00 -0600 reply
fricas)set output tex on
fricas)set output algebra off
integrate(exp(-x^2),x) 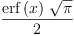
(5) Type: Union(Expression(Integer),...) Errorfunction- Wed, 23 Mar 2005 08:23:21 -0600 reply
fricasintegrate(exp(-x^2/2)/sqrt(%pi*2),
x=%minusInfinity..%plusInfinity) 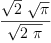
(6) Type: Union(f1: OrderedCompletion?(Expression(Integer)),...)
integrate(x^6*exp(-x^2/2)/sqrt(%pi*2),x=%minusInfinity..%plusInfinity)
| (7) |
integrate(x^6*exp(-x^2/2)/sqrt(%pi*2),x)
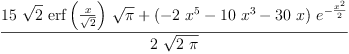 | (8) |
| (9) |
integrate(exp(x)/x^2,x)
| (10) |
integrate(sqrt(x),x)
| (11) |