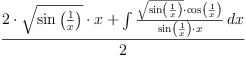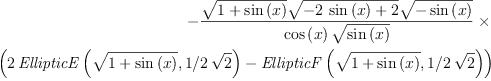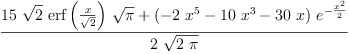Errors in symbolic integration Risch-Bronstein-Trager algorithm (Risch algorithm in short) is a complete algorithm for integration in terms of elementary functions. The algorithm either finds elementary integral or proves that there is none. Existence of elementary integral is relatively rare, so given random elementary function probably does not have elementary integral. FriCAS implementation of Risch algorithm is probably the "most complete" existing implementation. Unfortunately "most complete" does not mean complete, some parts are still unimplemented. See RischImplementationStatus. Unlike some other systems FriCAS will not give you unevaluated result when hitting unimplemented part. Instead, it signals error with message indicating that given integral requires unimplemented part. So when FriCAS returns unevaluated result almost surely there is no elementary integral. Almost surely, because as all programs FriCAS may have bugs... FriCAS in fact implements extension of Risch algorithm which extends class of integrands
to some Liouvillian functions and for integration in terms of Ei, Ci, Si, li, erf,
fresnelS, fresnelC, incomplete Gamma, polylogs and elliptic integrals. There is complete
extended algorithm for large class of functions. However
fricas (1) -> integrate(sin(x)+sqrt(1-x^3),
Type: Union(Expression(Integer),
Here FriCAS proved that result is not elementary and found integral in terms of elliptic functions. Below is result when we keep only algebraic part fricas integrate(sqrt(1-x^3),
Type: Union(Expression(Integer), Reduce code
2) fricas integrate(sqrt(1-log(sin(x)^2)), In this case FriCAS neither can compute elementary result nor can it prove that result is not elementary, so it gives up with error message indicating that the handling this integral requires unimplemented part of Bronstein-Trager algorithm. Reduce answer:
3) fricas integrate(sqrt(sin(1/x)), Again, this integral needs unimplemented part of Bronstein-Trager algorithm. Reduce reduce answer:
4) fricas )set output tex off fricas )set output algebra on Type: Union(Expression(Integer), This time FriCAS can prove that result is nonelementary and returns answer in terms of elliptic functions. Reduce answer:
For this Maple 9 gives the following result:
And Mathematica 4 gives:
fricas integrate(x^6*exp(-x^2/2)/sqrt(%pi*2),
Type: Union(f1: OrderedCompletion?(Expression(Integer)),
fricas integrate(x^6*exp(-x^2/2)/sqrt(%pi*2),
Type: Union(Expression(Integer),
... --unknown, Thu, 25 Aug 2005 05:57:53 -0500 reply fricas integrate(exp(x)/x^2,
Type: Union(Expression(Integer),
fricas integrate(sqrt(x),
Type: Union(Expression(Integer),
|
|
|
|
last edited 7 months ago by test1 |