|
|
|
last edited 4 years ago by pagani |
Edit detail for SandBoxTensorAlgebra3 revision 1 of 1
| 1 | ||
|
Editor: pagani
Time: 2020/11/03 19:33:59 GMT+0 |
||
| Note: | ||
changed: - \begin{spad} )abbrev domain TENSALG TensorAlgebra ++ Author: Kurt Pagani ++ Date Created: Thu Jan 30 23:04:02 CET 2020 ++ License: BSD ++ References: ++ https://en.wikipedia.org/wiki/Tensor_algebra ++ Description: ++ Quote Ref: ++ -- Non-commutative polynomials ++ -- Quotients ++ Because of the generality of the tensor algebra, many other algebras ++ of interest can be constructed by starting with the tensor algebra and ++ then imposing certain relations on the generators, i.e. by constructing ++ certain quotient algebras of T(V). Examples of this are the ++ exterior algebra, the symmetric algebra, Clifford algebras, ++ the Weyl algebra and universal enveloping algebras. ++ TensorAlgebra(M,R,B) : Exports == Implementation where M:FreeModuleCategory(R, B) R:Ring B:OrderedSet OF ==> OutputForm NNI ==> NonNegativeInteger FMB ==> FreeMonoid B CTOF ==> CoercibleTo OutputForm FMCRB ==> FreeModuleCategory(R,FMB) XFABR ==> XFreeAlgebra(B,R) XDPBR ==> XDistributedPolynomial(B,R) TERM ==> Record(k:FMB,c:R) Exports == Join(FMCRB, XFABR) with coerce : B -> % convert : FMB -> OutputForm Implementation == XDPBR add Rep := XDPBR convert(x:FMB):OutputForm == x=1$FMB => empty()$OF length(x)$FMB = 1 => x::OF length(x)$FMB = 2 => tensor(first(x)::OF,rest(x)::OF)$OF tensor(first(x)::OF, convert(rest x)) coerce(x:%):OutputForm == zero? x => empty()$OF x=1$% => outputForm(1)$OF c:R:=leadingCoefficient(x) if c=1 then cof:=empty()$OF else cof:=c::OF kof:OF:=cof * convert(leadingSupport(x)) zero? reductum(x) => kof kof + reductum(x)::OF )abbrev domain OOBJ OrderedObjectList ++ Description: ++ This domain implements ordered objects such that the type ++ has OrderedSet. Adapted from OrderedVariableList. OrderedObjectList(T:Comparable, ObjectList : List T): Join(OrderedFinite, ConvertibleTo T) with object : T -> Union(%,"failed") ++ object(s) returns a member of the object set or failed == add ObjectList := removeDuplicates ObjectList Rep := PositiveInteger s1, s2 : % convert(s1) : T == ObjectList.((s1::Rep)::PositiveInteger) coerce(s1) : OutputForm == (convert(s1)@T)::OutputForm index i == i::% lookup j == j :: Rep size () == #ObjectList object(exp : T) == for i in 1.. for exp2 in ObjectList repeat if exp = exp2 then return i::PositiveInteger::% "failed" s1 < s2 == s2 <$Rep s1 s1 = s2 == s1 =$Rep s2 latex(x : %) : String == latex(convert(x)@T) hashUpdate!(hs, s) == update!(hs, SXHASH(s)$Lisp)$HashState -- B:=OrderedObjectList(BOP, map(operator,[a,b,c])) -- index(1)$B -- enumerate()$B -- size()$B -- object(operator a)$B \end{spad} \begin{axiom} n:=3 B1:=OrderedVariableList [e[i] for i in 1..n] R1:=Expression Integer M1:=FreeModule(R1, B1) TA1:=TensorAlgebra(M1,R1,B1) e:=[a::TA1 for a in enumerate()$B1] T1:=x*e.1+y*e.2-z*e.3 T11:=T1*T1 --- B2:=OrderedObjectList(BOP, map(operator,[a,b,c])) R2:=DeRhamComplex(Integer,[x,y,z]) M2:=FreeModule(R2, B2) TA2:=TensorAlgebra(M2,R2,B2) g:=[a::TA2 for a in enumerate()$B2] h:=[generator(i)$R2 for i in 1..3] T2:=h.1*g.1+h.2*g.2-h.3*g.3 T3:=g.2 * T2 - T2 * g.1 T4:=h.2 * T3 )show TENSALG \end{axiom}
fricas
(1) -> <spad>
fricas
)abbrev domain TENSALG TensorAlgebra ++ Author: Kurt Pagani ++ Date Created: Thu Jan 30 23:04:02 CET 2020 ++ License: BSD ++ References: ++ https://en.wikipedia.org/wiki/Tensor_algebra ++ Description: ++ Quote Ref: ++ -- Non-commutative polynomials ++ -- Quotients ++ Because of the generality of the tensor algebra,many other algebras ++ of interest can be constructed by starting with the tensor algebra and ++ then imposing certain relations on the generators, i.e. by constructing ++ certain quotient algebras of T(V). Examples of this are the ++ exterior algebra, the symmetric algebra, Clifford algebras, ++ the Weyl algebra and universal enveloping algebras. ++ TensorAlgebra(M, R, B) : Exports == Implementation where
M:FreeModuleCategory(R,B) R:Ring B:OrderedSet
OF ==> OutputForm NNI ==> NonNegativeInteger FMB ==> FreeMonoid B CTOF ==> CoercibleTo OutputForm FMCRB ==> FreeModuleCategory(R,FMB) XFABR ==> XFreeAlgebra(B, R) XDPBR ==> XDistributedPolynomial(B, R) TERM ==> Record(k:FMB, c:R)
Exports == Join(FMCRB,XFABR) with
coerce : B -> % convert : FMB -> OutputForm
Implementation == XDPBR add
Rep := XDPBR
convert(x:FMB):OutputForm == x=1$FMB => empty()$OF length(x)$FMB = 1 => x::OF length(x)$FMB = 2 => tensor(first(x)::OF,rest(x)::OF)$OF tensor(first(x)::OF, convert(rest x))
coerce(x:%):OutputForm == zero? x => empty()$OF x=1$% => outputForm(1)$OF c:R:=leadingCoefficient(x) if c=1 then cof:=empty()$OF else cof:=c::OF kof:OF:=cof * convert(leadingSupport(x)) zero? reductum(x) => kof kof + reductum(x)::OF
fricas
)abbrev domain OOBJ OrderedObjectList ++ Description: ++ This domain implements ordered objects such that the type ++ has OrderedSet. Adapted from OrderedVariableList. OrderedObjectList(T:Comparable,ObjectList : List T): Join(OrderedFinite, ConvertibleTo T) with object : T -> Union(%, "failed") ++ object(s) returns a member of the object set or failed == add ObjectList := removeDuplicates ObjectList Rep := PositiveInteger s1, s2 : % convert(s1) : T == ObjectList.((s1::Rep)::PositiveInteger) coerce(s1) : OutputForm == (convert(s1)@T)::OutputForm index i == i::% lookup j == j :: Rep size () == #ObjectList object(exp : T) == for i in 1.. for exp2 in ObjectList repeat if exp = exp2 then return i::PositiveInteger::% "failed" s1 < s2 == s2 <$Rep s1 s1 = s2 == s1 =$Rep s2 latex(x : %) : String == latex(convert(x)@T) hashUpdate!(hs, s) == update!(hs, SXHASH(s)$Lisp)$HashState
-- B:=OrderedObjectList(BOP,map(operator, [a, b, c])) -- index(1)$B -- enumerate()$B -- size()$B -- object(operator a)$B</spad>
fricas
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/3277064617359698758-25px001.spad
using old system compiler.
TENSALG abbreviates domain TensorAlgebra
------------------------------------------------------------------------
initializing NRLIB TENSALG for TensorAlgebra
compiling into NRLIB TENSALG
compiling exported convert : FreeMonoid B -> OutputForm
Time: 0.02 SEC.
compiling exported coerce : % -> OutputForm
Time: 0 SEC.
****** Domain: R already in scope
augmenting R: (Comparable)
****** Domain: R already in scope
augmenting R: (CommutativeRing)
(time taken in buildFunctor: 4513)
Time: 0 SEC.
Cumulative Statistics for Constructor TensorAlgebra
Time: 0.03 seconds
--------------non extending category----------------------
.. TensorAlgebra(#1,
; wrote /var/aw/var/LatexWiki/TENSALG.NRLIB/TENSALG.fasl
; compilation finished in 0:00:00.028
------------------------------------------------------------------------
TensorAlgebra is now explicitly exposed in frame initial
TensorAlgebra will be automatically loaded when needed from
/var/aw/var/LatexWiki/TENSALG.NRLIB/TENSALG
OOBJ abbreviates domain OrderedObjectList
------------------------------------------------------------------------
initializing NRLIB OOBJ for OrderedObjectList
compiling into NRLIB OOBJ
****** Domain: T$ already in scope
Local variable Rep type redefined: (Join (OrderedAbelianSemiGroup) (OrderedMonoid) (CommutativeStar) (ConvertibleTo (InputForm)) (Hashable) (CATEGORY domain (SIGNATURE gcd (% % %)) (SIGNATURE qcoerce (% (Integer))))) to (Join (XPolynomialsCat B R) (FreeModuleCategory R (FreeMonoid B)))
compiling exported convert : % -> T$
Time: 0.01 SEC.
compiling exported coerce : % -> OutputForm
Time: 0 SEC.
compiling exported index : PositiveInteger -> %
OOBJ;index;Pi%;3 is replaced by i
Time: 0 SEC.
compiling exported lookup : % -> PositiveInteger
OOBJ;lookup;%Pi;4 is replaced by j
Time: 0 SEC.
compiling exported size : () -> NonNegativeInteger
Time: 0 SEC.
compiling exported object : T$ -> Union(%,
compiling exported < : (%,
compiling exported = : (%,
compiling exported latex : % -> String
Time: 0 SEC.
compiling exported hashUpdate! : (HashState,
(time taken in buildFunctor: 556)
Time: 0 SEC.
Cumulative Statistics for Constructor OrderedObjectList
Time: 0.02 seconds
finalizing NRLIB OOBJ
Processing OrderedObjectList for Browser database:
--------constructor---------
--------(object ((Union % failed) T$))---------
; compiling file "/var/aw/var/LatexWiki/OOBJ.NRLIB/OOBJ.lsp" (written 09 AUG 2025 10:08:27 AM):
; wrote /var/aw/var/LatexWiki/OOBJ.NRLIB/OOBJ.fasl
; compilation finished in 0:00:00.028
------------------------------------------------------------------------
OrderedObjectList is now explicitly exposed in frame initial
OrderedObjectList will be automatically loaded when needed from
/var/aw/var/LatexWiki/OOBJ.NRLIB/OOBJfricas
n:=3
 | (1) |
Type: PositiveInteger?
fricas
B1:=OrderedVariableList [e[i] for i in 1..n]
![\label{eq2}\hbox{\axiomType{OrderedVariableList}\ } \left({\left[{e_{1}}, \:{e_{2}}, \:{e_{3}}\right]}\right)](images/6854671562371173833-16.0px.png "\label{eq2}\hbox{\axiomType{OrderedVariableList}\ } \left({\left[{e_{1}}, \:{e_{2}}, \:{e_{3}}\right]}\right)") | (2) |
Type: Type
fricas
R1:=Expression Integer
 | (3) |
Type: Type
fricas
M1:=FreeModule(R1,B1)
![\label{eq4}\hbox{\axiomType{FreeModule}\ } \left({{\hbox{\axiomType{Expression}\ } \left({\hbox{\axiomType{Integer}\ }}\right)}, \:{\hbox{\axiomType{OrderedVariableList}\ } \left({\left[{e_{1}}, \:{e_{2}}, \:{e_{3}}\right]}\right)}}\right)](images/6747553549747686522-16.0px.png "\label{eq4}\hbox{\axiomType{FreeModule}\ } \left({{\hbox{\axiomType{Expression}\ } \left({\hbox{\axiomType{Integer}\ }}\right)}, \:{\hbox{\axiomType{OrderedVariableList}\ } \left({\left[{e_{1}}, \:{e_{2}}, \:{e_{3}}\right]}\right)}}\right)") | (4) |
Type: Type
fricas
TA1:=TensorAlgebra(M1,R1, B1)
![\label{eq5}\hbox{\axiomType{TensorAlgebra}\ } \left({{\hbox{\axiomType{FreeModule}\ } \left({{\hbox{\axiomType{Expression}\ } \left({\hbox{\axiomType{Integer}\ }}\right)}, \:{\hbox{\axiomType{OrderedVariableList}\ } \left({\left[{e_{1}}, \:{e_{2}}, \:{e_{3}}\right]}\right)}}\right)}, \:{\hbox{\axiomType{Expression}\ } \left({\hbox{\axiomType{Integer}\ }}\right)}, \:{\hbox{\axiomType{OrderedVariableList}\ } \left({\left[{e_{1}}, \:{e_{2}}, \:{e_{3}}\right]}\right)}}\right)](images/2743783191762621425-16.0px.png "\label{eq5}\hbox{\axiomType{TensorAlgebra}\ } \left({{\hbox{\axiomType{FreeModule}\ } \left({{\hbox{\axiomType{Expression}\ } \left({\hbox{\axiomType{Integer}\ }}\right)}, \:{\hbox{\axiomType{OrderedVariableList}\ } \left({\left[{e_{1}}, \:{e_{2}}, \:{e_{3}}\right]}\right)}}\right)}, \:{\hbox{\axiomType{Expression}\ } \left({\hbox{\axiomType{Integer}\ }}\right)}, \:{\hbox{\axiomType{OrderedVariableList}\ } \left({\left[{e_{1}}, \:{e_{2}}, \:{e_{3}}\right]}\right)}}\right)") | (5) |
Type: Type
fricas
e:=[a::TA1 for a in enumerate()$B1]
![\label{eq6}\left[{\ {e_{1}}}, \:{\ {e_{2}}}, \:{\ {e_{3}}}\right]](images/2500432007490566947-16.0px.png "\label{eq6}\left[{\ {e_{1}}}, \:{\ {e_{2}}}, \:{\ {e_{3}}}\right]") | (6) |
Type: List(TensorAlgebra?(FreeModule(Expression(Integer),
fricas
T1:=x*e.1+y*e.2-z*e.3
 | (7) |
Type: TensorAlgebra?(FreeModule(Expression(Integer),
fricas
T11:=T1*T1
![\label{eq8}\begin{array}{@{}l}
\displaystyle
{{{x}^{2}}\ {{e_{1}}\otimes{e_{1}}}}+{x \ y \ {{e_{1}}\otimes{e_{2}}}}-{x \ z \ {{e_{1}}\otimes{e_{3}}}}+
\
\
\displaystyle
{x \ y \ {{e_{2}}\otimes{e_{1}}}}+{{{y}^{2}}\ {{e_{2}}\otimes{e_{2}}}}-{y \ z \ {{e_{2}}\otimes{e_{3}}}}-
\
\
\displaystyle
{x \ z \ {{e_{3}}\otimes{e_{1}}}}-{y \ z \ {{e_{3}}\otimes{e_{2}}}}+{{{z}^{2}}\ {{e_{3}}\otimes{e_{3}}}}](images/7361074830312898928-16.0px.png "\label{eq8}\begin{array}{@{}l}
\displaystyle
{{{x}^{2}}\ {{e_{1}}\otimes{e_{1}}}}+{x \ y \ {{e_{1}}\otimes{e_{2}}}}-{x \ z \ {{e_{1}}\otimes{e_{3}}}}+
\
\
\displaystyle
{x \ y \ {{e_{2}}\otimes{e_{1}}}}+{{{y}^{2}}\ {{e_{2}}\otimes{e_{2}}}}-{y \ z \ {{e_{2}}\otimes{e_{3}}}}-
\
\
\displaystyle
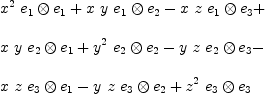{x \ z \ {{e_{3}}\otimes{e_{1}}}}-{y \ z \ {{e_{3}}\otimes{e_{2}}}}+{{{z}^{2}}\ {{e_{3}}\otimes{e_{3}}}}") | (8) |
Type: TensorAlgebra?(FreeModule(Expression(Integer),
fricas
--- B2:=OrderedObjectList(BOP,map(operator, [a, b, c]))
![\label{eq9}\hbox{\axiomType{OrderedObjectList}\ } \left({\hbox{\axiomType{BasicOperator}\ } , \:{\left[ a , \: b , \: c \right]}}\right)](images/8283178542414325053-16.0px.png "\label{eq9}\hbox{\axiomType{OrderedObjectList}\ } \left({\hbox{\axiomType{BasicOperator}\ } , \:{\left[ a , \: b , \: c \right]}}\right)") | (9) |
Type: Type
fricas
R2:=DeRhamComplex(Integer,[x, y, z])
![\label{eq10}\hbox{\axiomType{DeRhamComplex}\ } \left({\hbox{\axiomType{Integer}\ } , \:{\left[ x , \: y , \: z \right]}}\right)](images/2102471674507902610-16.0px.png "\label{eq10}\hbox{\axiomType{DeRhamComplex}\ } \left({\hbox{\axiomType{Integer}\ } , \:{\left[ x , \: y , \: z \right]}}\right)") | (10) |
Type: Type
fricas
M2:=FreeModule(R2,B2)
![\label{eq11}\hbox{\axiomType{FreeModule}\ } \left({{\hbox{\axiomType{DeRhamComplex}\ } \left({\hbox{\axiomType{Integer}\ } , \:{\left[ x , \: y , \: z \right]}}\right)}, \:{\hbox{\axiomType{OrderedObjectList}\ } \left({\hbox{\axiomType{BasicOperator}\ } , \:{\left[ a , \: b , \: c \right]}}\right)}}\right)](images/7816248359765191215-16.0px.png "\label{eq11}\hbox{\axiomType{FreeModule}\ } \left({{\hbox{\axiomType{DeRhamComplex}\ } \left({\hbox{\axiomType{Integer}\ } , \:{\left[ x , \: y , \: z \right]}}\right)}, \:{\hbox{\axiomType{OrderedObjectList}\ } \left({\hbox{\axiomType{BasicOperator}\ } , \:{\left[ a , \: b , \: c \right]}}\right)}}\right)") | (11) |
Type: Type
fricas
TA2:=TensorAlgebra(M2,R2, B2)
![\label{eq12}\hbox{\axiomType{TensorAlgebra}\ } \left({{\hbox{\axiomType{FreeModule}\ } \left({{\hbox{\axiomType{DeRhamComplex}\ } \left({\hbox{\axiomType{Integer}\ } , \:{\left[ x , \: y , \: z \right]}}\right)}, \:{\hbox{\axiomType{OrderedObjectList}\ } \left({\hbox{\axiomType{BasicOperator}\ } , \:{\left[ a , \: b , \: c \right]}}\right)}}\right)}, \:{\hbox{\axiomType{DeRhamComplex}\ } \left({\hbox{\axiomType{Integer}\ } , \:{\left[ x , \: y , \: z \right]}}\right)}, \:{\hbox{\axiomType{OrderedObjectList}\ } \left({\hbox{\axiomType{BasicOperator}\ } , \:{\left[ a , \: b , \: c \right]}}\right)}}\right)](images/3982157463552141378-16.0px.png "\label{eq12}\hbox{\axiomType{TensorAlgebra}\ } \left({{\hbox{\axiomType{FreeModule}\ } \left({{\hbox{\axiomType{DeRhamComplex}\ } \left({\hbox{\axiomType{Integer}\ } , \:{\left[ x , \: y , \: z \right]}}\right)}, \:{\hbox{\axiomType{OrderedObjectList}\ } \left({\hbox{\axiomType{BasicOperator}\ } , \:{\left[ a , \: b , \: c \right]}}\right)}}\right)}, \:{\hbox{\axiomType{DeRhamComplex}\ } \left({\hbox{\axiomType{Integer}\ } , \:{\left[ x , \: y , \: z \right]}}\right)}, \:{\hbox{\axiomType{OrderedObjectList}\ } \left({\hbox{\axiomType{BasicOperator}\ } , \:{\left[ a , \: b , \: c \right]}}\right)}}\right)") | (12) |
Type: Type
fricas
g:=[a::TA2 for a in enumerate()$B2]
![\label{eq13}\left[{\ a}, \:{\ b}, \:{\ c}\right]](images/782915223677107193-16.0px.png "\label{eq13}\left[{\ a}, \:{\ b}, \:{\ c}\right]") | (13) |
Type: List(TensorAlgebra?(FreeModule(DeRhamComplex?(Integer,
fricas
h:=[generator(i)$R2 for i in 1..3]
![\label{eq14}\left[ dx , \: dy , \: dz \right]](images/4524090445907504999-16.0px.png "\label{eq14}\left[ dx , \: dy , \: dz \right]") | (14) |
fricas
T2:=h.1*g.1+h.2*g.2-h.3*g.3
 | (15) |
Type: TensorAlgebra?(FreeModule(DeRhamComplex?(Integer,
fricas
T3:=g.2 * T2 - T2 * g.1
![\label{eq16}\begin{array}{@{}l}
\displaystyle
-{dx \ {a \otimes a}}+{{\left(- dy + dx \right)}\ {b \otimes a}}+{dy \ {b \otimes b}}-
\
\
\displaystyle
{dz \ {b \otimes c}}+{dz \ {c \otimes a}}](images/1190886619837943122-16.0px.png "\label{eq16}\begin{array}{@{}l}
\displaystyle
-{dx \ {a \otimes a}}+{{\left(- dy + dx \right)}\ {b \otimes a}}+{dy \ {b \otimes b}}-
\
\
\displaystyle
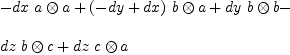{dz \ {b \otimes c}}+{dz \ {c \otimes a}}") | (16) |
Type: TensorAlgebra?(FreeModule(DeRhamComplex?(Integer,
fricas
T4:=h.2 * T3
![\label{eq17}\begin{array}{@{}l}
\displaystyle
{dx \ dy \ {a \otimes a}}-{dx \ dy \ {b \otimes a}}-{dy \ dz \ {b \otimes c}}+
\
\
\displaystyle
{dy \ dz \ {c \otimes a}}](images/3127845189858916110-16.0px.png "\label{eq17}\begin{array}{@{}l}
\displaystyle
{dx \ dy \ {a \otimes a}}-{dx \ dy \ {b \otimes a}}-{dy \ dz \ {b \otimes c}}+
\
\
\displaystyle
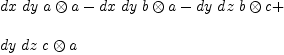{dy \ dz \ {c \otimes a}}") | (17) |
Type: TensorAlgebra?(FreeModule(DeRhamComplex?(Integer,
fricas
)show TENSALG
TensorAlgebra(M: FreeModuleCategory(R,B), R: Ring, B: OrderedSet) is a domain constructor Abbreviation for TensorAlgebra is TENSALG This constructor is exposed in this frame. ------------------------------- Operations --------------------------------
?*? : (%,%) -> % ?*? : (Integer, %) -> % ?*? : (B, %) -> % ?*? : (%, R) -> % ?*? : (R, %) -> % ?*? : (PositiveInteger, %) -> % ?+? : (%, %) -> % ?-? : (%, %) -> % -? : % -> % ?=? : (%, %) -> Boolean 1 : () -> % 0 : () -> % ?^? : (%, PositiveInteger) -> % annihilate? : (%, %) -> Boolean antiCommutator : (%, %) -> % associator : (%, %, %) -> % coef : (%, FreeMonoid(B)) -> R coef : (%, %) -> R coefficients : % -> List(R) coerce : Integer -> % coerce : R -> % coerce : FreeMonoid(B) -> % coerce : B -> % coerce : % -> OutputForm commutator : (%, %) -> % constant : % -> R constant? : % -> Boolean latex : % -> String lquo : (%, B) -> % lquo : (%, FreeMonoid(B)) -> % lquo : (%, %) -> % map : ((R -> R), %) -> % mindeg : % -> FreeMonoid(B) mirror : % -> % monomial? : % -> Boolean monomials : % -> List(%) one? : % -> Boolean opposite? : (%, %) -> Boolean quasiRegular : % -> % quasiRegular? : % -> Boolean recip : % -> Union(%, "failed") retract : % -> R retract : % -> FreeMonoid(B) rquo : (%, B) -> % rquo : (%, FreeMonoid(B)) -> % rquo : (%, %) -> % sample : () -> % varList : % -> List(B) zero? : % -> Boolean ?~=? : (%, %) -> Boolean ?*? : (NonNegativeInteger, %) -> % ?^? : (%, NonNegativeInteger) -> % characteristic : () -> NonNegativeInteger coefficient : (%, FreeMonoid(B)) -> R construct : List(Record(k: FreeMonoid(B), c: R)) -> % constructOrdered : List(Record(k: FreeMonoid(B), c: R)) -> % if FreeMonoid(B) has COMPAR convert : FreeMonoid(B) -> OutputForm leadingCoefficient : % -> R if FreeMonoid(B) has COMPAR leadingMonomial : % -> % if FreeMonoid(B) has COMPAR leadingSupport : % -> FreeMonoid(B) if FreeMonoid(B) has COMPAR leadingTerm : % -> Record(k: FreeMonoid(B), c: R) if FreeMonoid(B) has COMPAR leftPower : (%, PositiveInteger) -> % leftPower : (%, NonNegativeInteger) -> % leftRecip : % -> Union(%, "failed") linearExtend : ((FreeMonoid(B) -> R), %) -> R if R has COMRING listOfTerms : % -> List(Record(k: FreeMonoid(B), c: R)) mindegTerm : % -> Record(k: FreeMonoid(B), c: R) monomial : (R, FreeMonoid(B)) -> % numberOfMonomials : % -> NonNegativeInteger plenaryPower : (%, PositiveInteger) -> % if R has COMRING reductum : % -> % if FreeMonoid(B) has COMPAR retractIfCan : % -> Union(R, "failed") retractIfCan : % -> Union(FreeMonoid(B), "failed") rightPower : (%, PositiveInteger) -> % rightPower : (%, NonNegativeInteger) -> % rightRecip : % -> Union(%, "failed") sh : (%, %) -> % if R has COMRING sh : (%, NonNegativeInteger) -> % if R has COMRING smaller? : (%, %) -> Boolean if R has COMPAR and FreeMonoid(B) has COMPAR subtractIfCan : (%, %) -> Union(%, "failed") support : % -> List(FreeMonoid(B))