EigenVectors? and Diagonalization
fricas
(1) -> ℂ:=Complex Fraction Polynomial Integer
Type: Type
fricas
-- dagger
htranspose(h)==map(x+->conjugate(x),transpose h)
Type: Void
fricas
)expose MCALCFN
MultiVariableCalculusFunctions is now explicitly exposed in frame
initial
fricas
)set output tex off
fricas
)set output algebra on
fricas
p1:ℂ:=complex(ℜp1,𝔍p1)
(3) ℜp1 + 𝔍p1 %i
Type: Complex(Fraction(Polynomial(Integer)))
fricas
q1:ℂ:=complex(ℜq1,𝔍q1)
(4) ℜq1 + 𝔍q1 %i
Type: Complex(Fraction(Polynomial(Integer)))
fricas
p2:ℂ:=complex(ℜp2,𝔍p2)
(5) ℜp2 + 𝔍p2 %i
Type: Complex(Fraction(Polynomial(Integer)))
fricas
q2:ℂ:=complex(ℜq2,𝔍q2)
(6) ℜq2 + 𝔍q2 %i
Type: Complex(Fraction(Polynomial(Integer)))
fricas
ρ:Matrix ℂ := matrix [[p1,q1],[p2,q2]]
+ℜp1 + 𝔍p1 %i ℜq1 + 𝔍q1 %i+
(7) | |
+ℜp2 + 𝔍p2 %i ℜq2 + 𝔍q2 %i+
Type: Matrix(Complex(Fraction(Polynomial(Integer))))
fricas
s1:=solve(imag determinant ρ,ℜp2)
ℜp1 𝔍q2 - ℜq1 𝔍p2 + ℜq2 𝔍p1
(8) [ℜp2 = ---------------------------]
𝔍q1
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
s2:=solve(eval(imag trace ρ,s1),𝔍p1)
(9) [𝔍p1 = - 𝔍q2]
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
s3:=solve(eval(eval(imag trace(ρ*ρ),s1), s2),ℜp1)
(10) [0 = 0]
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
eval(eval(imag trace (ρ*ρ),s1),s2)
(11) 0
Type: Fraction(Polynomial(Integer))
fricas
C:=eval(eval(characteristicPolynomial ρ,s1),s2)
(12)
2 2
𝔍q1 𝔍q2 + (ℜq1 ℜq2 - ℜp1 ℜq1)𝔍q2 + 𝔍p2 𝔍q1
+
2 2
((ℜp1 - %B)ℜq2 - %B ℜp1 + %B )𝔍q1 + ℜq1 𝔍p2
/
𝔍q1
Type: Fraction(Polynomial(Complex(Integer)))
fricas
C0:=zerosOf(C)
(13)
[
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
ℜq2 + ℜp1
/
2
,
-
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
ℜq2 + ℜp1
/
2
]
Type: List(Expression(Complex(Integer)))
fricas
#C0
(14) 2
fricas
imag(C0.1)
(15) 0
Type: Expression(Integer)
fricas
imag(C0.2)
(16) 0
Type: Expression(Integer)
Given an operator 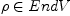 , one must find the tensor
, one must find the tensor 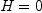 for unknown manifold of hermitian isomorphisms
for unknown manifold of hermitian isomorphisms 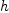 .
.
fricas
h:Matrix ℂ:=matrix [[ℜa,complex(ℜb,𝔍b)],[complex(ℜb,-𝔍b),ℜe]]
+ ℜa ℜb + 𝔍b %i+
(17) | |
+ℜb - 𝔍b %i ℜe +
Type: Matrix(Complex(Fraction(Polynomial(Integer))))
fricas
test(h = htranspose h)
fricas
Compiling function htranspose with type Matrix(Complex(Fraction(
Polynomial(Integer)))) -> Matrix(Complex(Fraction(Polynomial(
Integer))))
(18) trueType: Boolean
fricas
H:=htranspose(ρ)*h-h*ρ
(19)
[
[(- 2 ℜb 𝔍p2 - 2 ℜa 𝔍p1 - 2 ℜp2 𝔍b)%i,
𝔍b 𝔍q2 + 𝔍b 𝔍p1 - ℜb ℜq2 - ℜa ℜq1 + ℜe ℜp2 + ℜb ℜp1
+
(- ℜb 𝔍q2 - ℜa 𝔍q1 - ℜe 𝔍p2 - ℜb 𝔍p1 + (- ℜq2 + ℜp1)𝔍b)%i
]
,
[
- 𝔍b 𝔍q2 - 𝔍b 𝔍p1 + ℜb ℜq2 + ℜa ℜq1 - ℜe ℜp2 - ℜb ℜp1
+
(- ℜb 𝔍q2 - ℜa 𝔍q1 - ℜe 𝔍p2 - ℜb 𝔍p1 + (- ℜq2 + ℜp1)𝔍b)%i
,
(- 2 ℜe 𝔍q2 - 2 ℜb 𝔍q1 + 2 ℜq1 𝔍b)%i]
]
Type: Matrix(Complex(Fraction(Polynomial(Integer))))
We wish to find expressions for 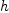 in terms of the components of
in terms of the components of
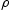 . To do this we will determine how the components of
. To do this we will determine how the components of 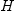 depend
on the components of
depend
on the components of 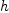 .
.
fricas
J:=jacobian(concat( map(x+->[real x, imag x], concat(H::List List ?)) ),
[ℜa,ℜb,𝔍b,ℜe]::List Symbol)
+ 0 0 0 0 +
| |
|- 2 𝔍p1 - 2 𝔍p2 - 2 ℜp2 0 |
| |
| - ℜq1 - ℜq2 + ℜp1 𝔍q2 + 𝔍p1 ℜp2 |
| |
| - 𝔍q1 - 𝔍q2 - 𝔍p1 - ℜq2 + ℜp1 - 𝔍p2 |
(20) | |
| ℜq1 ℜq2 - ℜp1 - 𝔍q2 - 𝔍p1 - ℜp2 |
| |
| - 𝔍q1 - 𝔍q2 - 𝔍p1 - ℜq2 + ℜp1 - 𝔍p2 |
| |
| 0 0 0 0 |
| |
+ 0 - 2 𝔍q1 2 ℜq1 - 2 𝔍q2+
Type: Matrix(Fraction(Polynomial(Integer)))
The null space (kernel) of the Jacobian
fricas
N:=nullSpace(map(x+->eval(eval(x,s1),s2),J))
- ℜq2 + ℜp1 ℜq1 𝔍p2 𝔍q2
(21) [[-----------, ---, 1, 0], [- ---, - ---, 0, 1]]
𝔍q1 𝔍q1 𝔍q1 𝔍q1
Type: List(Vector(Fraction(Polynomial(Integer))))
gives the general solution to the problem.
fricas
s4:=map((x,y)+->x=y,[ℜa,ℜb,𝔍b,ℜe],𝔍b*N.1+ℜe*N.2)
(22)
- ℜe 𝔍p2 + (- ℜq2 + ℜp1)𝔍b - ℜe 𝔍q2 + ℜq1 𝔍b
[ℜa = --------------------------, ℜb = -----------------, 𝔍b = 𝔍b, ℜe = ℜe]
𝔍q1 𝔍q1
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
H0:=map(x+->eval(eval(eval(x,s1),s2),s4),H)
+0 0+
(23) | |
+0 0+
Type: Matrix(Fraction(Polynomial(Complex(Integer))))
fricas
h0:=map(x+->eval(eval(eval(x,s1),s2),s4),h)
+ - ℜe 𝔍p2 + (- ℜq2 + ℜp1)𝔍b - ℜe 𝔍q2 + %i 𝔍b 𝔍q1 + ℜq1 𝔍b+
| -------------------------- -----------------------------|
| 𝔍q1 𝔍q1 |
(24) | |
|- ℜe 𝔍q2 - %i 𝔍b 𝔍q1 + ℜq1 𝔍b |
|----------------------------- ℜe |
+ 𝔍q1 +
Type: Matrix(Fraction(Polynomial(Complex(Integer))))
fricas
ρ0:=map(x+->eval(eval(x,s1),s2),ρ)
+ - %i 𝔍q2 + ℜp1 %i 𝔍q1 + ℜq1+
| |
(25) |(- ℜq2 + ℜp1)𝔍q2 + %i 𝔍p2 𝔍q1 - ℜq1 𝔍p2 |
|--------------------------------------- %i 𝔍q2 + ℜq2|
+ 𝔍q1 +
Type: Matrix(Fraction(Polynomial(Complex(Integer))))
fricas
E:=eigenvalues(ρ0)
(26)
[
%D
|
2 2
𝔍q1 𝔍q2 + (ℜq1 ℜq2 - ℜp1 ℜq1)𝔍q2 + 𝔍p2 𝔍q1
+
2 2
((ℜp1 - %D)ℜq2 - %D ℜp1 + %D )𝔍q1 + ℜq1 𝔍p2
]
Type: List(Union(Fraction(Polynomial(Complex(Integer))),
SuchThat
?(Symbol,
Polynomial(Complex(Integer)))))
fricas
E0:=eigenvector(E.1,ρ0)
+ %i 𝔍q1 𝔍q2 + (ℜq2 - %D)𝔍q1 +
|-------------------------------------|
(27) [|(ℜq2 - ℜp1)𝔍q2 - %i 𝔍p2 𝔍q1 + ℜq1 𝔍p2|]
| |
+ 1 +
Type: List(Matrix(Fraction(Polynomial(Complex(Integer)))))
fricas
E1:=map(x+->eval(x,%D=C0.1),E0.1)
(28)
[
[
-
𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2 %i 𝔍q1 𝔍q2 + (ℜq2 - ℜp1)𝔍q1
/
(2 ℜq2 - 2 ℜp1)𝔍q2 - 2 %i 𝔍p2 𝔍q1 + 2 ℜq1 𝔍p2
]
,
[1]]
Type: Matrix(Expression(Complex(Integer)))
fricas
E2:=map(x+->eval(x,%D=C0.2),E0.1)
(29)
[
[
𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2 %i 𝔍q1 𝔍q2 + (ℜq2 - ℜp1)𝔍q1
/
(2 ℜq2 - 2 ℜp1)𝔍q2 - 2 %i 𝔍p2 𝔍q1 + 2 ℜq1 𝔍p2
]
,
[1]]
Type: Matrix(Expression(Complex(Integer)))
fricas
test(ρ0*E1=C0(1)*E1)
(30) true
Type: Boolean
fricas
test(ρ0*E2=C0(2)*E2)
(31) true
Type: Boolean
fricas
EE := horizConcat(E1,E2)
(32)
[
[
-
𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2 %i 𝔍q1 𝔍q2 + (ℜq2 - ℜp1)𝔍q1
/
(2 ℜq2 - 2 ℜp1)𝔍q2 - 2 %i 𝔍p2 𝔍q1 + 2 ℜq1 𝔍p2
,
𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2 %i 𝔍q1 𝔍q2 + (ℜq2 - ℜp1)𝔍q1
/
(2 ℜq2 - 2 ℜp1)𝔍q2 - 2 %i 𝔍p2 𝔍q1 + 2 ℜq1 𝔍p2
]
,
[1, 1]]
Type: Matrix(Expression(Complex(Integer)))
fricas
EI := inverse EE
(33)
[
[
(- ℜq2 + ℜp1)𝔍q2 + %i 𝔍p2 𝔍q1 - ℜq1 𝔍p2
/
𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
,
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2 %i 𝔍q2 + ℜq2 - ℜp1
/
2
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
]
,
[
(ℜq2 - ℜp1)𝔍q2 - %i 𝔍p2 𝔍q1 + ℜq1 𝔍p2
/
𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
,
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
- 2 %i 𝔍q2 - ℜq2 + ℜp1
/
2
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
]
]
Type: Union(Matrix(Expression(Complex(Integer))),...)
fricas
ρ1:=EI*ρ0*EE
(34)
[
[
(ℜq2 + ℜp1)𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
2 𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
,
0]
,
[0,
(ℜq2 + ℜp1)𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2 2
4 𝔍q1 𝔍q2 + (4 ℜq1 ℜq2 - 4 ℜp1 ℜq1)𝔍q2 + 4 𝔍p2 𝔍q1
+
2 2 2
(- ℜq2 + 2 ℜp1 ℜq2 - ℜp1 )𝔍q1 + 4 ℜq1 𝔍p2
/
2 𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
]
]
Type: Matrix(Expression(Complex(Integer)))
fricas
h1:=map(x+->eval(eval(x,s1),s2),h)
+ ℜa %i 𝔍b + ℜb+
(35) | |
+- %i 𝔍b + ℜb ℜe +
Type: Matrix(Fraction(Polynomial(Complex(Integer))))
fricas
hh:=EI*h1*EE
(36)
[
[
(ℜe + ℜa)𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
(2 %i ℜe - 2 %i ℜa)𝔍q1 + (- 2 %i ℜq2 + 2 %i ℜp1)𝔍b - 2 ℜb ℜq2
+
2 ℜb ℜp1
*
𝔍q2
+
2
(2 𝔍b + 2 %i ℜb)𝔍q1
+
(- 2 𝔍b + 2 %i ℜb)𝔍p2 - 2 %i ℜq1 𝔍b + (ℜe - ℜa)ℜq2 + 2 ℜb ℜq1
+
(- ℜe + ℜa)ℜp1
*
𝔍q1
+
(- 2 %i ℜq1 𝔍b - 2 ℜb ℜq1)𝔍p2
/
2 𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
,
2
((2 𝔍b + 2 %i ℜb)𝔍q1 + ((ℜe - ℜa)ℜq2 + (- ℜe + ℜa)ℜp1)𝔍q1)𝔍q2
+
(- %i ℜe + %i ℜa)𝔍p2 + (- %i ℜq2 + %i ℜp1)𝔍b + ℜb ℜq2
+
- ℜb ℜp1
*
2
𝔍q1
+
(ℜe - ℜa)ℜq1 𝔍p2 𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2
(4 %i 𝔍b - 4 ℜb)𝔍q1
+
((2 %i ℜe - 2 %i ℜa)ℜq2 + (- 2 %i ℜe + 2 %i ℜa)ℜp1)𝔍q1
+
2 2 2
(- 2 %i ℜq2 + 4 %i ℜp1 ℜq2 - 2 %i ℜp1 )𝔍b - 2 ℜb ℜq2
+
2
4 ℜb ℜp1 ℜq2 - 2 ℜb ℜp1
*
2
𝔍q2
+
(2 ℜe - 2 ℜa)𝔍p2 + (2 ℜq2 - 2 ℜp1)𝔍b + 2 %i ℜb ℜq2
+
- 2 %i ℜb ℜp1
*
2
𝔍q1
+
(- 4 ℜq2 + 4 ℜp1)𝔍b + 4 %i ℜb ℜq2
+
(2 %i ℜe - 2 %i ℜa)ℜq1 - 4 %i ℜb ℜp1
*
𝔍p2
+
2
(2 %i ℜq1 ℜq2 - 2 %i ℜp1 ℜq1)𝔍b + (ℜe - ℜa)ℜq2
+
(- 2 ℜb ℜq1 + (- 2 ℜe + 2 ℜa)ℜp1)ℜq2 + 2 ℜb ℜp1 ℜq1
+
2
(ℜe - ℜa)ℜp1
*
𝔍q1
+
(- 4 %i ℜq1 ℜq2 + 4 %i ℜp1 ℜq1)𝔍b - 4 ℜb ℜq1 ℜq2
+
4 ℜb ℜp1 ℜq1
*
𝔍p2
*
𝔍q2
+
3
(2 %i 𝔍b - 2 ℜb)𝔍p2 𝔍q1
+
2
(2 %i 𝔍b + 2 ℜb)𝔍p2
+
((- %i ℜe + %i ℜa)ℜq2 + (%i ℜe - %i ℜa)ℜp1)𝔍p2
+
2 2 2
(- %i ℜq2 + 2 %i ℜp1 ℜq2 - %i ℜp1 )𝔍b + ℜb ℜq2 - 2 ℜb ℜp1 ℜq2
+
2
ℜb ℜp1
*
2
𝔍q1
+
2
(- 4 ℜq1 𝔍b + 4 %i ℜb ℜq1)𝔍p2
+
2 2
2 %i ℜq1 𝔍b + (ℜe - ℜa)ℜq1 ℜq2 - 2 ℜb ℜq1
+
(- ℜe + ℜa)ℜp1 ℜq1
*
𝔍p2
*
𝔍q1
+
2 2 2
(- 2 %i ℜq1 𝔍b - 2 ℜb ℜq1 )𝔍p2
/
2
((2 ℜq2 - 2 ℜp1)𝔍q1 𝔍q2 - 2 %i 𝔍p2 𝔍q1 + 2 ℜq1 𝔍p2 𝔍q1)
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
]
,
[
2
((2 𝔍b + 2 %i ℜb)𝔍q1 + ((ℜe - ℜa)ℜq2 + (- ℜe + ℜa)ℜp1)𝔍q1)𝔍q2
+
(- %i ℜe + %i ℜa)𝔍p2 + (- %i ℜq2 + %i ℜp1)𝔍b + ℜb ℜq2
+
- ℜb ℜp1
*
2
𝔍q1
+
(ℜe - ℜa)ℜq1 𝔍p2 𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2
(- 4 %i 𝔍b + 4 ℜb)𝔍q1
+
((- 2 %i ℜe + 2 %i ℜa)ℜq2 + (2 %i ℜe - 2 %i ℜa)ℜp1)𝔍q1
+
2 2 2
(2 %i ℜq2 - 4 %i ℜp1 ℜq2 + 2 %i ℜp1 )𝔍b + 2 ℜb ℜq2
+
2
- 4 ℜb ℜp1 ℜq2 + 2 ℜb ℜp1
*
2
𝔍q2
+
(- 2 ℜe + 2 ℜa)𝔍p2 + (- 2 ℜq2 + 2 ℜp1)𝔍b - 2 %i ℜb ℜq2
+
2 %i ℜb ℜp1
*
2
𝔍q1
+
(4 ℜq2 - 4 ℜp1)𝔍b - 4 %i ℜb ℜq2
+
(- 2 %i ℜe + 2 %i ℜa)ℜq1 + 4 %i ℜb ℜp1
*
𝔍p2
+
2
(- 2 %i ℜq1 ℜq2 + 2 %i ℜp1 ℜq1)𝔍b + (- ℜe + ℜa)ℜq2
+
(2 ℜb ℜq1 + (2 ℜe - 2 ℜa)ℜp1)ℜq2 - 2 ℜb ℜp1 ℜq1
+
2
(- ℜe + ℜa)ℜp1
*
𝔍q1
+
((4 %i ℜq1 ℜq2 - 4 %i ℜp1 ℜq1)𝔍b + 4 ℜb ℜq1 ℜq2 - 4 ℜb ℜp1 ℜq1)𝔍p2
*
𝔍q2
+
3
(- 2 %i 𝔍b + 2 ℜb)𝔍p2 𝔍q1
+
2
(- 2 %i 𝔍b - 2 ℜb)𝔍p2
+
((%i ℜe - %i ℜa)ℜq2 + (- %i ℜe + %i ℜa)ℜp1)𝔍p2
+
2 2 2
(%i ℜq2 - 2 %i ℜp1 ℜq2 + %i ℜp1 )𝔍b - ℜb ℜq2 + 2 ℜb ℜp1 ℜq2
+
2
- ℜb ℜp1
*
2
𝔍q1
+
2
(4 ℜq1 𝔍b - 4 %i ℜb ℜq1)𝔍p2
+
2 2
- 2 %i ℜq1 𝔍b + (- ℜe + ℜa)ℜq1 ℜq2 + 2 ℜb ℜq1
+
(ℜe - ℜa)ℜp1 ℜq1
*
𝔍p2
*
𝔍q1
+
2 2 2
(2 %i ℜq1 𝔍b + 2 ℜb ℜq1 )𝔍p2
/
2
((2 ℜq2 - 2 ℜp1)𝔍q1 𝔍q2 - 2 %i 𝔍p2 𝔍q1 + 2 ℜq1 𝔍p2 𝔍q1)
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
,
(ℜe + ℜa)𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
(- 2 %i ℜe + 2 %i ℜa)𝔍q1 + (2 %i ℜq2 - 2 %i ℜp1)𝔍b + 2 ℜb ℜq2
+
- 2 ℜb ℜp1
*
𝔍q2
+
2
(- 2 𝔍b - 2 %i ℜb)𝔍q1
+
(2 𝔍b - 2 %i ℜb)𝔍p2 + 2 %i ℜq1 𝔍b + (- ℜe + ℜa)ℜq2 - 2 ℜb ℜq1
+
(ℜe - ℜa)ℜp1
*
𝔍q1
+
(2 %i ℜq1 𝔍b + 2 ℜb ℜq1)𝔍p2
/
2 𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
]
]
Type: Matrix(Expression(Complex(Integer)))
fricas
htranspose(h)==map(x+->conjugate(x::Complex Expression Integer),transpose h)
Compiled code for htranspose has been cleared.
1 old definition(s) deleted for function or rule htranspose
Type: Void
fricas
H1:=htranspose(ρ1)*hh-hh*ρ1
fricas
Compiling function htranspose with type Matrix(Expression(Complex(
Integer))) -> Matrix(Complex(Expression(Integer)))
(38)
[
[0,
2
((2 𝔍b + 2 %i ℜb)𝔍q1 + ((ℜe - ℜa)ℜq2 + (- ℜe + ℜa)ℜp1)𝔍q1)𝔍q2
+
(- %i ℜe + %i ℜa)𝔍p2 + (- %i ℜq2 + %i ℜp1)𝔍b + ℜb ℜq2
+
- ℜb ℜp1
*
2
𝔍q1
+
(ℜe - ℜa)ℜq1 𝔍p2 𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2
(4 %i 𝔍b - 4 ℜb)𝔍q1
+
((2 %i ℜe - 2 %i ℜa)ℜq2 + (- 2 %i ℜe + 2 %i ℜa)ℜp1)𝔍q1
+
2 2 2
(- 2 %i ℜq2 + 4 %i ℜp1 ℜq2 - 2 %i ℜp1 )𝔍b - 2 ℜb ℜq2
+
2
4 ℜb ℜp1 ℜq2 - 2 ℜb ℜp1
*
2
𝔍q2
+
(2 ℜe - 2 ℜa)𝔍p2 + (2 ℜq2 - 2 ℜp1)𝔍b + 2 %i ℜb ℜq2
+
- 2 %i ℜb ℜp1
*
2
𝔍q1
+
(- 4 ℜq2 + 4 ℜp1)𝔍b + 4 %i ℜb ℜq2
+
(2 %i ℜe - 2 %i ℜa)ℜq1 - 4 %i ℜb ℜp1
*
𝔍p2
+
2
(2 %i ℜq1 ℜq2 - 2 %i ℜp1 ℜq1)𝔍b + (ℜe - ℜa)ℜq2
+
(- 2 ℜb ℜq1 + (- 2 ℜe + 2 ℜa)ℜp1)ℜq2 + 2 ℜb ℜp1 ℜq1
+
2
(ℜe - ℜa)ℜp1
*
𝔍q1
+
(- 4 %i ℜq1 ℜq2 + 4 %i ℜp1 ℜq1)𝔍b - 4 ℜb ℜq1 ℜq2
+
4 ℜb ℜp1 ℜq1
*
𝔍p2
*
𝔍q2
+
3
(2 %i 𝔍b - 2 ℜb)𝔍p2 𝔍q1
+
2
(2 %i 𝔍b + 2 ℜb)𝔍p2
+
((- %i ℜe + %i ℜa)ℜq2 + (%i ℜe - %i ℜa)ℜp1)𝔍p2
+
2 2 2
(- %i ℜq2 + 2 %i ℜp1 ℜq2 - %i ℜp1 )𝔍b + ℜb ℜq2 - 2 ℜb ℜp1 ℜq2
+
2
ℜb ℜp1
*
2
𝔍q1
+
2
(- 4 ℜq1 𝔍b + 4 %i ℜb ℜq1)𝔍p2
+
2 2
2 %i ℜq1 𝔍b + (ℜe - ℜa)ℜq1 ℜq2 - 2 ℜb ℜq1
+
(- ℜe + ℜa)ℜp1 ℜq1
*
𝔍p2
*
𝔍q1
+
2 2 2
(- 2 %i ℜq1 𝔍b - 2 ℜb ℜq1 )𝔍p2
/
2
(2 ℜq2 - 2 ℜp1)𝔍q1 𝔍q2 - 2 %i 𝔍p2 𝔍q1 + 2 ℜq1 𝔍p2 𝔍q1
]
,
[
2
((- 2 𝔍b - 2 %i ℜb)𝔍q1 + ((- ℜe + ℜa)ℜq2 + (ℜe - ℜa)ℜp1)𝔍q1)𝔍q2
+
2
((%i ℜe - %i ℜa)𝔍p2 + (%i ℜq2 - %i ℜp1)𝔍b - ℜb ℜq2 + ℜb ℜp1)𝔍q1
+
(- ℜe + ℜa)ℜq1 𝔍p2 𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2
(4 %i 𝔍b - 4 ℜb)𝔍q1
+
((2 %i ℜe - 2 %i ℜa)ℜq2 + (- 2 %i ℜe + 2 %i ℜa)ℜp1)𝔍q1
+
2 2 2
(- 2 %i ℜq2 + 4 %i ℜp1 ℜq2 - 2 %i ℜp1 )𝔍b - 2 ℜb ℜq2
+
2
4 ℜb ℜp1 ℜq2 - 2 ℜb ℜp1
*
2
𝔍q2
+
(2 ℜe - 2 ℜa)𝔍p2 + (2 ℜq2 - 2 ℜp1)𝔍b + 2 %i ℜb ℜq2
+
- 2 %i ℜb ℜp1
*
2
𝔍q1
+
(- 4 ℜq2 + 4 ℜp1)𝔍b + 4 %i ℜb ℜq2
+
(2 %i ℜe - 2 %i ℜa)ℜq1 - 4 %i ℜb ℜp1
*
𝔍p2
+
2
(2 %i ℜq1 ℜq2 - 2 %i ℜp1 ℜq1)𝔍b + (ℜe - ℜa)ℜq2
+
(- 2 ℜb ℜq1 + (- 2 ℜe + 2 ℜa)ℜp1)ℜq2 + 2 ℜb ℜp1 ℜq1
+
2
(ℜe - ℜa)ℜp1
*
𝔍q1
+
(- 4 %i ℜq1 ℜq2 + 4 %i ℜp1 ℜq1)𝔍b - 4 ℜb ℜq1 ℜq2
+
4 ℜb ℜp1 ℜq1
*
𝔍p2
*
𝔍q2
+
3
(2 %i 𝔍b - 2 ℜb)𝔍p2 𝔍q1
+
2
(2 %i 𝔍b + 2 ℜb)𝔍p2
+
((- %i ℜe + %i ℜa)ℜq2 + (%i ℜe - %i ℜa)ℜp1)𝔍p2
+
2 2 2
(- %i ℜq2 + 2 %i ℜp1 ℜq2 - %i ℜp1 )𝔍b + ℜb ℜq2 - 2 ℜb ℜp1 ℜq2
+
2
ℜb ℜp1
*
2
𝔍q1
+
2
(- 4 ℜq1 𝔍b + 4 %i ℜb ℜq1)𝔍p2
+
2 2
2 %i ℜq1 𝔍b + (ℜe - ℜa)ℜq1 ℜq2 - 2 ℜb ℜq1
+
(- ℜe + ℜa)ℜp1 ℜq1
*
𝔍p2
*
𝔍q1
+
2 2 2
(- 2 %i ℜq1 𝔍b - 2 ℜb ℜq1 )𝔍p2
/
2
(2 ℜq2 - 2 ℜp1)𝔍q1 𝔍q2 - 2 %i 𝔍p2 𝔍q1 + 2 ℜq1 𝔍p2 𝔍q1
,
0]
]Type: Matrix(Expression(Complex(Integer)))
fricas
J1:=jacobian(concat( map(x+->[real x, imag x], concat(H1::List List ?)) ),
[ℜa,ℜb,𝔍b,ℜe]::List Symbol)
(39)
[[0, 0, 0, 0], [0, 0, 0, 0],
[
-
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
- ℜq2 + ℜp1
/
2
,
3 2 2 2
(- 2 𝔍p2 𝔍q1 + (ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 )𝔍q2
+
2
(ℜq1 ℜq2 - ℜp1 ℜq1)𝔍p2 𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2 3 2 2 3
((- 4 ℜq2 + 4 ℜp1)𝔍q1 - 2 ℜq2 + 6 ℜp1 ℜq2 - 6 ℜp1 ℜq2 + 2 ℜp1 )
*
3
𝔍q2
+
2 2 2
- 4 ℜq1 𝔍p2 𝔍q1 + (- 2 ℜq1 ℜq2 + 4 ℜp1 ℜq1 ℜq2 - 2 ℜp1 ℜq1)𝔍q1
+
2 2
(- 6 ℜq1 ℜq2 + 12 ℜp1 ℜq1 ℜq2 - 6 ℜp1 ℜq1)𝔍p2
*
2
𝔍q2
+
3
(- 4 ℜq2 + 4 ℜp1)𝔍p2 𝔍q1
+
2 3 2 2 3
((- 2 ℜq2 + 2 ℜp1)𝔍p2 + ℜq2 - 3 ℜp1 ℜq2 + 3 ℜp1 ℜq2 - ℜp1 )
*
2
𝔍q1
+
2 2 2 2 2
(- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1 )𝔍p2 𝔍q1 + (- 6 ℜq1 ℜq2 + 6 ℜp1 ℜq1 )𝔍p2
*
𝔍q2
+
2 3
- 2 ℜq1 𝔍p2 𝔍q1
+
3 2 2 2
(- 2 ℜq1 𝔍p2 + (ℜq1 ℜq2 - 2 ℜp1 ℜq1 ℜq2 + ℜp1 ℜq1)𝔍p2)𝔍q1
+
3 2 3 3
- 2 ℜq1 𝔍p2 𝔍q1 - 2 ℜq1 𝔍p2
/
2 2 2
(2 ℜq2 - 4 ℜp1 ℜq2 + 2 ℜp1 )𝔍q1 𝔍q2
+
2 3 2 2
(4 ℜq1 ℜq2 - 4 ℜp1 ℜq1)𝔍p2 𝔍q1 𝔍q2 + 2 𝔍p2 𝔍q1 + 2 ℜq1 𝔍p2 𝔍q1
,
2 2
((2 ℜq2 - 2 ℜp1)𝔍q1 𝔍q2 + 2 ℜq1 𝔍p2 𝔍q1 𝔍q2 + (ℜq2 - ℜp1)𝔍p2 𝔍q1 )
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2 2 2
- 4 𝔍p2 𝔍q1 + (2 ℜq2 - 4 ℜp1 ℜq2 + 2 ℜp1 )𝔍q1
+
2 2
(- 2 ℜq2 + 4 ℜp1 ℜq2 - 2 ℜp1 )𝔍p2
*
2
𝔍q2
+
2 2 3
(- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍p2 𝔍q2 - 2 𝔍p2 𝔍q1
+
3 2 2 2 2 2
(- 2 𝔍p2 + (ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍p2)𝔍q1 - 2 ℜq1 𝔍p2 𝔍q1
+
2 3
- 2 ℜq1 𝔍p2
/
2 2 2
(2 ℜq2 - 4 ℜp1 ℜq2 + 2 ℜp1 )𝔍q2 + (4 ℜq1 ℜq2 - 4 ℜp1 ℜq1)𝔍p2 𝔍q2
+
2 2 2 2
2 𝔍p2 𝔍q1 + 2 ℜq1 𝔍p2
,
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
ℜq2 - ℜp1
/
2
]
,
[- 𝔍q2,
2 2
((2 ℜq2 - 2 ℜp1)𝔍q1 𝔍q2 + 2 ℜq1 𝔍p2 𝔍q1 𝔍q2 + (ℜq2 - ℜp1)𝔍p2 𝔍q1 )
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2 2 2
- 4 𝔍p2 𝔍q1 + (2 ℜq2 - 4 ℜp1 ℜq2 + 2 ℜp1 )𝔍q1
+
2 2
(2 ℜq2 - 4 ℜp1 ℜq2 + 2 ℜp1 )𝔍p2
*
2
𝔍q2
+
2 2 3
(4 ℜq1 ℜq2 - 4 ℜp1 ℜq1)𝔍p2 𝔍q2 - 2 𝔍p2 𝔍q1
+
3 2 2 2 2 2
(2 𝔍p2 + (ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍p2)𝔍q1 - 2 ℜq1 𝔍p2 𝔍q1
+
2 3
2 ℜq1 𝔍p2
/
2 2 2
(2 ℜq2 - 4 ℜp1 ℜq2 + 2 ℜp1 )𝔍q2 + (4 ℜq1 ℜq2 - 4 ℜp1 ℜq1)𝔍p2 𝔍q2
+
2 2 2 2
2 𝔍p2 𝔍q1 + 2 ℜq1 𝔍p2
,
3 2 2 2
(2 𝔍p2 𝔍q1 + (- ℜq2 + 2 ℜp1 ℜq2 - ℜp1 )𝔍q1 )𝔍q2
+
2
(- ℜq1 ℜq2 + ℜp1 ℜq1)𝔍p2 𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2 3 2 2 3 3
((4 ℜq2 - 4 ℜp1)𝔍q1 - 2 ℜq2 + 6 ℜp1 ℜq2 - 6 ℜp1 ℜq2 + 2 ℜp1 )𝔍q2
+
2 2 2
4 ℜq1 𝔍p2 𝔍q1 + (2 ℜq1 ℜq2 - 4 ℜp1 ℜq1 ℜq2 + 2 ℜp1 ℜq1)𝔍q1
+
2 2
(- 6 ℜq1 ℜq2 + 12 ℜp1 ℜq1 ℜq2 - 6 ℜp1 ℜq1)𝔍p2
*
2
𝔍q2
+
3
(4 ℜq2 - 4 ℜp1)𝔍p2 𝔍q1
+
2 3 2 2 3
((- 2 ℜq2 + 2 ℜp1)𝔍p2 - ℜq2 + 3 ℜp1 ℜq2 - 3 ℜp1 ℜq2 + ℜp1 )
*
2
𝔍q1
+
2 2 2 2 2
(4 ℜq1 ℜq2 - 4 ℜp1 ℜq1 )𝔍p2 𝔍q1 + (- 6 ℜq1 ℜq2 + 6 ℜp1 ℜq1 )𝔍p2
*
𝔍q2
+
2 3
2 ℜq1 𝔍p2 𝔍q1
+
3 2 2 2
(- 2 ℜq1 𝔍p2 + (- ℜq1 ℜq2 + 2 ℜp1 ℜq1 ℜq2 - ℜp1 ℜq1)𝔍p2)𝔍q1
+
3 2 3 3
2 ℜq1 𝔍p2 𝔍q1 - 2 ℜq1 𝔍p2
/
2 2 2
(2 ℜq2 - 4 ℜp1 ℜq2 + 2 ℜp1 )𝔍q1 𝔍q2
+
2 3 2 2
(4 ℜq1 ℜq2 - 4 ℜp1 ℜq1)𝔍p2 𝔍q1 𝔍q2 + 2 𝔍p2 𝔍q1 + 2 ℜq1 𝔍p2 𝔍q1
,
𝔍q2]
,
[
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
- ℜq2 + ℜp1
/
2
,
3 2 2 2
(2 𝔍p2 𝔍q1 + (- ℜq2 + 2 ℜp1 ℜq2 - ℜp1 )𝔍q1 )𝔍q2
+
2
(- ℜq1 ℜq2 + ℜp1 ℜq1)𝔍p2 𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2 3 2 2 3
((- 4 ℜq2 + 4 ℜp1)𝔍q1 - 2 ℜq2 + 6 ℜp1 ℜq2 - 6 ℜp1 ℜq2 + 2 ℜp1 )
*
3
𝔍q2
+
2 2 2
- 4 ℜq1 𝔍p2 𝔍q1 + (- 2 ℜq1 ℜq2 + 4 ℜp1 ℜq1 ℜq2 - 2 ℜp1 ℜq1)𝔍q1
+
2 2
(- 6 ℜq1 ℜq2 + 12 ℜp1 ℜq1 ℜq2 - 6 ℜp1 ℜq1)𝔍p2
*
2
𝔍q2
+
3
(- 4 ℜq2 + 4 ℜp1)𝔍p2 𝔍q1
+
2 3 2 2 3
((- 2 ℜq2 + 2 ℜp1)𝔍p2 + ℜq2 - 3 ℜp1 ℜq2 + 3 ℜp1 ℜq2 - ℜp1 )
*
2
𝔍q1
+
2 2 2 2 2
(- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1 )𝔍p2 𝔍q1 + (- 6 ℜq1 ℜq2 + 6 ℜp1 ℜq1 )𝔍p2
*
𝔍q2
+
2 3
- 2 ℜq1 𝔍p2 𝔍q1
+
3 2 2 2
(- 2 ℜq1 𝔍p2 + (ℜq1 ℜq2 - 2 ℜp1 ℜq1 ℜq2 + ℜp1 ℜq1)𝔍p2)𝔍q1
+
3 2 3 3
- 2 ℜq1 𝔍p2 𝔍q1 - 2 ℜq1 𝔍p2
/
2 2 2
(2 ℜq2 - 4 ℜp1 ℜq2 + 2 ℜp1 )𝔍q1 𝔍q2
+
2 3 2 2
(4 ℜq1 ℜq2 - 4 ℜp1 ℜq1)𝔍p2 𝔍q1 𝔍q2 + 2 𝔍p2 𝔍q1 + 2 ℜq1 𝔍p2 𝔍q1
,
2
(- 2 ℜq2 + 2 ℜp1)𝔍q1 𝔍q2 - 2 ℜq1 𝔍p2 𝔍q1 𝔍q2
+
2
(- ℜq2 + ℜp1)𝔍p2 𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2 2 2
- 4 𝔍p2 𝔍q1 + (2 ℜq2 - 4 ℜp1 ℜq2 + 2 ℜp1 )𝔍q1
+
2 2
(- 2 ℜq2 + 4 ℜp1 ℜq2 - 2 ℜp1 )𝔍p2
*
2
𝔍q2
+
2 2 3
(- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍p2 𝔍q2 - 2 𝔍p2 𝔍q1
+
3 2 2 2 2 2
(- 2 𝔍p2 + (ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍p2)𝔍q1 - 2 ℜq1 𝔍p2 𝔍q1
+
2 3
- 2 ℜq1 𝔍p2
/
2 2 2
(2 ℜq2 - 4 ℜp1 ℜq2 + 2 ℜp1 )𝔍q2 + (4 ℜq1 ℜq2 - 4 ℜp1 ℜq1)𝔍p2 𝔍q2
+
2 2 2 2
2 𝔍p2 𝔍q1 + 2 ℜq1 𝔍p2
,
-
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
ℜq2 - ℜp1
/
2
]
,
[- 𝔍q2,
2
(- 2 ℜq2 + 2 ℜp1)𝔍q1 𝔍q2 - 2 ℜq1 𝔍p2 𝔍q1 𝔍q2
+
2
(- ℜq2 + ℜp1)𝔍p2 𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2 2 2
- 4 𝔍p2 𝔍q1 + (2 ℜq2 - 4 ℜp1 ℜq2 + 2 ℜp1 )𝔍q1
+
2 2
(2 ℜq2 - 4 ℜp1 ℜq2 + 2 ℜp1 )𝔍p2
*
2
𝔍q2
+
2 2 3
(4 ℜq1 ℜq2 - 4 ℜp1 ℜq1)𝔍p2 𝔍q2 - 2 𝔍p2 𝔍q1
+
3 2 2 2 2 2
(2 𝔍p2 + (ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍p2)𝔍q1 - 2 ℜq1 𝔍p2 𝔍q1
+
2 3
2 ℜq1 𝔍p2
/
2 2 2
(2 ℜq2 - 4 ℜp1 ℜq2 + 2 ℜp1 )𝔍q2 + (4 ℜq1 ℜq2 - 4 ℜp1 ℜq1)𝔍p2 𝔍q2
+
2 2 2 2
2 𝔍p2 𝔍q1 + 2 ℜq1 𝔍p2
,
3 2 2 2
(- 2 𝔍p2 𝔍q1 + (ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 )𝔍q2
+
2
(ℜq1 ℜq2 - ℜp1 ℜq1)𝔍p2 𝔍q1
*
ROOT
2 2
- 4 𝔍q1 𝔍q2 + (- 4 ℜq1 ℜq2 + 4 ℜp1 ℜq1)𝔍q2 - 4 𝔍p2 𝔍q1
+
2 2 2
(ℜq2 - 2 ℜp1 ℜq2 + ℜp1 )𝔍q1 - 4 ℜq1 𝔍p2
/
𝔍q1
+
2 3 2 2 3 3
((4 ℜq2 - 4 ℜp1)𝔍q1 - 2 ℜq2 + 6 ℜp1 ℜq2 - 6 ℜp1 ℜq2 + 2 ℜp1 )𝔍q2
+
2 2 2
4 ℜq1 𝔍p2 𝔍q1 + (2 ℜq1 ℜq2 - 4 ℜp1 ℜq1 ℜq2 + 2 ℜp1 ℜq1)𝔍q1
+
2 2
(- 6 ℜq1 ℜq2 + 12 ℜp1 ℜq1 ℜq2 - 6 ℜp1 ℜq1)𝔍p2
*
2
𝔍q2
+
3
(4 ℜq2 - 4 ℜp1)𝔍p2 𝔍q1
+
2 3 2 2 3
((- 2 ℜq2 + 2 ℜp1)𝔍p2 - ℜq2 + 3 ℜp1 ℜq2 - 3 ℜp1 ℜq2 + ℜp1 )
*
2
𝔍q1
+
2 2 2 2 2
(4 ℜq1 ℜq2 - 4 ℜp1 ℜq1 )𝔍p2 𝔍q1 + (- 6 ℜq1 ℜq2 + 6 ℜp1 ℜq1 )𝔍p2
*
𝔍q2
+
2 3
2 ℜq1 𝔍p2 𝔍q1
+
3 2 2 2
(- 2 ℜq1 𝔍p2 + (- ℜq1 ℜq2 + 2 ℜp1 ℜq1 ℜq2 - ℜp1 ℜq1)𝔍p2)𝔍q1
+
3 2 3 3
2 ℜq1 𝔍p2 𝔍q1 - 2 ℜq1 𝔍p2
/
2 2 2
(2 ℜq2 - 4 ℜp1 ℜq2 + 2 ℜp1 )𝔍q1 𝔍q2
+
2 3 2 2
(4 ℜq1 ℜq2 - 4 ℜp1 ℜq1)𝔍p2 𝔍q1 𝔍q2 + 2 𝔍p2 𝔍q1 + 2 ℜq1 𝔍p2 𝔍q1
,
𝔍q2]
,
[0, 0, 0, 0], [0, 0, 0, 0]]
Type: Matrix(Expression(Integer))
fricas
N1:=nullSpace(map(x+->eval(eval(x,s1),s2),J1))
(40) [[1, 0, 0, 1]]
Type: List(Vector(Expression(Integer)))
fricas
s5:=map((x,y)+->x=y,[ℜa,ℜb,𝔍b,ℜe],t*N1.1)
(41) [ℜa = t, ℜb = 0, 𝔍b = 0, ℜe = t]
Type: List(Equation(Expression(Integer)))
fricas
map(x+->eval(x,s5),H1)
+0 0+
(42) | |
+0 0+
Type: Matrix(Expression(Complex(Integer)))
fricas
h2:=EE*map(x+->eval(x,s5),hh)*EI
+t 0+
(43) | |
+0 t+
Type: Matrix(Expression(Complex(Integer)))
fricas
H0:=map(x+->eval(eval(eval(x,s1),s2),s5),H)
(44)
[
[2 %i t 𝔍q2,
2
(- t ℜq2 + t ℜp1)𝔍q2 - %i t 𝔍q1 + (- %i t 𝔍p2 - t ℜq1)𝔍q1 - t ℜq1 𝔍p2
----------------------------------------------------------------------]
𝔍q1
,
2
(t ℜq2 - t ℜp1)𝔍q2 - %i t 𝔍q1 + (- %i t 𝔍p2 + t ℜq1)𝔍q1 + t ℜq1 𝔍p2
[--------------------------------------------------------------------,
𝔍q1
- 2 %i t 𝔍q2]
]
Type: Matrix(Expression(Complex(Integer)))