Edit detail for SandBoxFrobeniusAlgebra revision 21 of 26

References

• Frobenius algebras and 2D topological quantum field theories by Joachim Kock

  Especially "Tensor calculus (linear algebra in coordinates)" in section 2.3.31, page 123.

See also:

• http://ncatlab.org/nlab/show/Frobenius+algebra by John Baez, et al.
• Ideals, Varieties, and Algorithms by David A. Cox, et al.

An n-dimensional algebra is represented by a (2,1)-tensor viewed as an operator with two inputs and one output . For example in 2 dimensions

n:=2

(1)

T:=CartesianTensor(1,n,FRAC POLY INT)

(2)

Y:T := unravel(concat concat
  [[[script(y,[[i,j],[k]])
    for i in 1..n]
      for j in 1..n]
        for k in 1..n]
          )

(3)

Given two vectors and

P:T := unravel([script(p,[[],[i]]) for i in 1..n])

(4)

Q:T := unravel([script(q,[[],[i]]) for i in 1..n])

(5)

the tensor operates on their tensor product to yield a vector

R:=contract(contract(Y,3,product(P,Q),1),2,3)

(6)

Pictorially:

  P Q
   Y
   R

  or more explicitly

  Pi Qj
   \/
    \
     Rk

In Axiom we may use the more convenient tensor inner product denoted by * that combines tensor product with a contraction on the last index of the first tensor and the first index of the second tensor.

R:=(Y*P)*Q

(7)

An algebra is said to be associative if:

  Y    =    Y
   Y       Y

Note: the right hand side of the equation above is implicitly the mirror image of the left hand side:

  i   j   k   i  j     k   i     j  k
   \  |  /     \/     /     \     \/
    \ | /       \    /       \    /
     \|/    =    e  k    -    i  e
      |           \/           \/
      |            \           /
      l             l         l

This requires that the following (3,1)-tensor

(8)

(associator) is zero.

YY := reindex(reindex(Y,[1,3,2])*reindex(Y,[1,3,2]),[1,4,3,2])-Y*Y; ravel(YY)

(9)

The algebra is commutative if:

  Y = Y

  i   j     i  j     j  i
   \ /   =   \/   -   \/
    |         \       /
    k          k     k

This requires that the following (2,1)-tensor

(10)

(commutator) is zero.

YC:=Y-reindex(Y,[1,3,2])

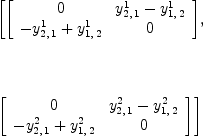(11)

A basis for the ideal defined by the coefficients of the commutator is given by:

groebner(ravel(YC))

(12)

The algebra is anti-commutative if:

  Y = -Y

  i   j     i  j     j  i
   \ /   =   \/   =   \/
    |         \       /
    k          k     k

This requires that the following (2,1)-tensor

(13)

(anti-commutator) is zero.

YA:=Y+reindex(Y,[1,3,2])

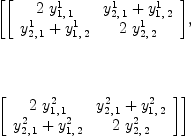(14)

A basis for the ideal defined by the coefficients of the commutator is given by:

groebner(ravel(YA))

(15)

The Jacobi identity is:

            X
  Y =  Y + Y
   Y  Y     Y

  i     j     k  i      j     k  i     j      k   i  j   k
   \    |    /    \    /     /    \     \    /     \  \ /
    \   |   /      \  /     /      \     \  /       \  0
     \  |  /        \/     /        \     \/         \/ \
      \ | /          \    /          \    /           \  \
       \|/     =      e  k      -     i  e       -     e  j
        |              \/              \/               \/
        |               \              /                /
        l                l            l                 l

An algebra satisfies the Jacobi identity if and only if the following (3,1)-tensor

(16)

is zero.

YX := YY - reindex(contract(Y,1,Y,2),[3,1,4,2]); ravel(YX)

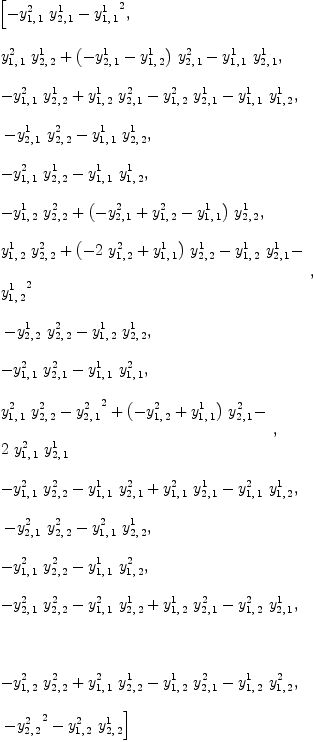(17)

A scalar product is denoted by the (2,0)-tensor

U:T := unravel(concat
  [[script(u,[[],[j,i]])
    for i in 1..n]
      for j in 1..n]
        )

(18)

Definition 1

We say that the scalar product is associative if the tensor equation holds:

    Y   =   Y
     U     U

In other words, if the (3,0)-tensor:

    i  j  k   i  j  k   i  j  k
     \ | /     \/  /     \  \/
      \|/   =   \ /   -   \ /
       0         0         0

(19)

(three-point function) is zero.

YU := reindex(reindex(U,[2,1])*reindex(Y,[1,3,2]),[3,2,1])-U*Y

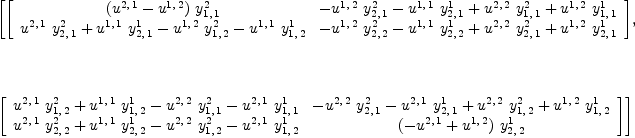(20)

Definition 2

An algebra with a non-degenerate associative scalar product is called pre-Frobenius.

We may consider the problem where multiplication Y is given, and look for all associative scalar products or we may consider an scalar product U as given, and look for all algebras such that the scalar product is associative.

This problem can be solved using linear algebra.

)expose MCALCFN

   MultiVariableCalculusFunctions is now explicitly exposed in frame 
      initial 
K := jacobian(ravel(YU),concat(map(variables,ravel(Y)))::List Symbol);

yy := transpose matrix [concat(map(variables,ravel(Y)))::List Symbol];

K::OutputForm * yy::OutputForm = 0

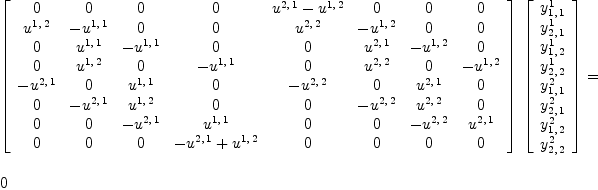(21)

The matrix K transforms the coefficients of the tensor into coefficients of the tensor . We are looking for coefficients of the tensor such that K transforms the tensor into for any .

A necessary condition for the equation to have a non-trivial solution is that the matrix K be degenerate.

Theorem 1

All 2-dimensional pre-Frobenius algebras are symmetric.

Proof: Consider the determinant of the matrix K above.

Kd := factor(determinant(K)::DMP(concat map(variables,ravel(U)),FRAC INT))

(22)

The scalar product must also be non-degenerate

Ud:DMP(concat map(variables,ravel(U)),FRAC INT) := determinant [[U[i,j] for j in 1..n] for i in 1..n]

(23)

therefore U must be symmetric.

nthFactor(Kd,1)

(24)

US:T := unravel(map(x+->subst(x,U[2,1]=U[1,2]),ravel U))

(25)

Theorem 2

All 2-dimensional algebras with associative scalar product are commutative.

Proof: The basis of the null space of the symmetric K matrix are all symmetric

YUS:T :=  reindex(reindex(US,[2,1])*reindex(Y,[1,3,2]),[3,2,1])-US*Y

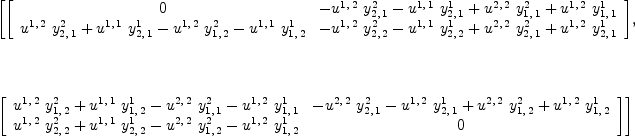(26)

KS := jacobian(ravel(YUS),concat(map(variables,ravel(Y)))::List Symbol);

NS:=nullSpace(KS)

(27)

SS:=map((x,y)+->x=y,concat map(variables,ravel Y),
  entries reduce(+,[p[i]*NS.i for i in 1..#NS]))

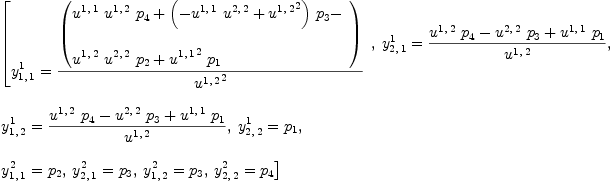(28)

YS:T := unravel(map(x+->subst(x,SS),ravel Y))

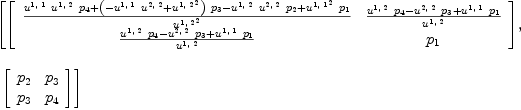(29)

This defines a 4-parameter family of 2-d pre-Frobenius algebras

test(unravel(map(x+->subst(x,SS),ravel YUS))$T=0*YU)

(30)

Alternatively we may consider

J := jacobian(ravel(YU),concat(map(variables,ravel(U)))::List Symbol);

uu := transpose matrix [concat(map(variables,ravel(U)))::List Symbol];

J::OutputForm * uu::OutputForm = 0

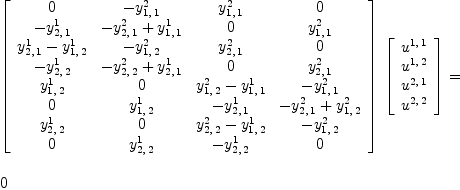(31)

The matrix J transforms the coefficients of the tensor into coefficients of the tensor . We are looking for coefficients of the tensor such that J transforms the tensor into for any .

A necessary condition for the equation to have a non-trivial solution is that all 70 of the 4x4 sub-matrices of J are degenerate. To this end we can form the polynomial ideal of the determinants of these sub-matrices.

JP:=ideal concat concat concat
  [[[[ determinant(
    matrix([row(J,i1),row(J,i2),row(J,i3),row(J,i4)]))
      for i4 in (i3+1)..maxRowIndex(J) ] 
        for i3 in (i2+1)..(maxRowIndex(J)-1) ]
          for i2 in (i1+1)..(maxRowIndex(J)-2) ]
            for i1 in minRowIndex(J)..(maxRowIndex(J)-3) ];

#generators(%)

(32)

Theorem 3

If a 2-d algebra is associative, commutative, anti-commutative or if it satisfies the Jacobi identity then it is a pre-Frobenius algebra.

Proof

in?(JP,ideal ravel YY)  -- associative

(33)

in?(JP,ideal ravel YC)  -- commutative

(34)

in?(JP,ideal ravel YA)  -- anti-commutative

(35)

in?(JP,ideal ravel YX) -- Jacobi identity

(36)

Y-forms

Left snail and right snail:

  LS                    RS

  Y A                   A Y
   Y )                 ( Y
    U                   U

  i  j                          j  i
   \/     0                0     \/
    \    / \              / \    /
     e  f   \            /   f  e
      \/     \          /     \/
       \     /          \     /
        \   /            \   /
         \ /              \ /
          0                0

(37)

LS=contract(Y*Y,1,2)

(38)

RS=reindex(contract(reindex(Y,[1,3,2])*reindex(Y,[1,3,2]),1,2),[2,1])

(39)

test(LS=RS)

(40)