MathAction SandBoxFrobeniusAlgebra

Topics

FrontPage
- FriCASContributions
  - Frobenius Algebra, Vector Spaces and Polynomial Ideals
    - SandBoxFrobeniusAlgebra <-- You are here.

References

Frobenius algebras and 2D topological quantum field theories by Joachim Kock
Especially "Tensor calculus (linear algebra in coordinates)" in section 2.3.31, page 123.

2-d Example

fricas

(1) -> )lib CARTEN MONAL PROP LOP

   >> System error:
   The value
  15684
is not of type
  LIST

Algebra

An n-dimensional algebra is represented by a (2,1)-tensor 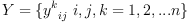$Y=\{ {y^k}_{ij} \ i,j,k =1,2, ... n \}$ viewed as a linear operator with two inputs 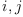and one output 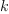. For example in 2 dimensions

fricas

Y:=Σ(Σ(Σ(script(y,[[i,j],[k]]),dx,i),dx,j),Dx,k)

   There are no library operations named Σ 
      Use HyperDoc Browse or issue
                                 )what op Σ
      to learn if there is any operation containing " Σ " in its name.

   Cannot find a definition or applicable library operation named Σ 
      with argument type(s) 
                                   Symbol
                                Variable(dx)
                                 Variable(i)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Multiplication

Given two vectors 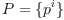$P=\{ p^i \}$ and $Q=\{ q^j \}$

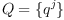
fricas

P:=Σ(script(p,[[],[i]]),Dx,i)

   There are no library operations named Σ 
      Use HyperDoc Browse or issue
                                 )what op Σ
      to learn if there is any operation containing " Σ " in its name.

   Cannot find a definition or applicable library operation named Σ 
      with argument type(s) 
                                   Symbol
                                Variable(Dx)
                                 Variable(i)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

the tensor 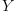operates on their tensor product to yield a vector $R=\{ r_k = {y^k}_{ij} p^i q^j \}$

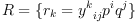
fricas

R:=(P,Q)/Y

   There are 11 exposed and 15 unexposed library operations named / 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op /
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named / 
      with argument type(s) 
                      Tuple(OrderedVariableList([P,Q]))
                                 Variable(Y)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Pictorially:

  P Q
   Y
   R

  or more explicitly

  Pi Qj
   \/
    \
     Rk

Associator

An algebra is said to be associative if:

    Y    =    Y
     Y       Y

    i   j   k   i  j     k   i     j  k
     \  |  /     \/     /     \     \/
      \ | /       \    /       \    /
       \|/    =    e  k    -    i  e
        |           \/           \/
        |            \           /
        l             l         l

This requires that the following (3,1)-tensor

$\label{eq1} \Psi = \{ {\psi_l}^{ijk} = {y^e}_{ij} {y^l}_{ek} - {y^l}_{ie} {y^e}_{jk} \}$

(1)

(associator) is zero.

fricas

YY := (Y,I)/Y - (I,Y)/Y

   There are 11 exposed and 15 unexposed library operations named / 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op /
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named / 
      with argument type(s) 
                      Tuple(OrderedVariableList([Y,I]))
                                 Variable(Y)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Commutator

The algebra 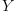is commutative if:

    Y = Y

    i   j     i  j     j  i
     \ /   =   \/   -   \/
      |         \       /
      k          k     k

This requires that the following (2,1)-tensor

$\label{eq2} \mathcal{C} = \{ {c^k}_{ij} = {y^k}_{ij} - {y^k}_{ji} \}$

(2)

(commutator) is zero.

fricas

YC:=Y-(X/Y)

$\label{eq3}\frac{{{Y}^{2}}- X}{Y}$

(3)

Type: Fraction(Polynomial(Integer))

A basis for the ideal defined by the coefficients of the commutator is given by:

fricas

groebner(ravel(YC))

   There are 1 exposed and 0 unexposed library operations named ravel 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op ravel
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named ravel
      with argument type(s) 
                        Fraction(Polynomial(Integer))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Anti-commutator

The algebra 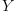is anti-commutative if:

    Y = -Y

    i   j     i  j     j  i
     \ /   =   \/   =   \/
      |         \       /
      k          k     k

This requires that the following (2,1)-tensor

$\label{eq4} \mathcal{A} = \{ {a^k}_{ij} = {y^k}_{ij} + {y^k}_{ji} \}$

(4)

(anti-commutator) is zero.

fricas

YA:=Y+(X/Y)

$\label{eq5}\frac{{{Y}^{2}}+ X}{Y}$

(5)

Type: Fraction(Polynomial(Integer))

A basis for the ideal defined by the coefficients of the commutator is given by:

fricas

groebner(ravel(YA))

   There are 1 exposed and 0 unexposed library operations named ravel 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op ravel
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named ravel
      with argument type(s) 
                        Fraction(Polynomial(Integer))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Jacobi

The Jacobi identity is:

              X
    Y =  Y + Y
     Y  Y     Y

    i     j     k  i      j     k  i     j      k   i  j   k
     \    |    /    \    /     /    \     \    /     \  \ /
      \   |   /      \  /     /      \     \  /       \  0
       \  |  /        \/     /        \     \/         \/ \
        \ | /          \    /          \    /           \  \
         \|/     =      e  k      -     i  e       -     e  j
          |              \/              \/               \/
          |               \              /                /
          l                l            l                 l

An algebra satisfies the Jacobi identity if and only if the following (3,1)-tensor

$\label{eq6} \Theta = \{ {\theta^l}_{ijk} = {y^l}_{ek} {y^e}_{ij} - {y^l}_{ie} {y^e}_{jk} - {y^l}_{ej} {y^e}_{ik} \}$

(6)

is zero.

fricas

YX := YY - (I,X)/(Y,I)/Y

   There are 11 exposed and 15 unexposed library operations named / 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op /
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named / 
      with argument type(s) 
                      Tuple(OrderedVariableList([I,X]))
                      Tuple(OrderedVariableList([Y,I]))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Scalar Product

A scalar product is denoted by the (2,0)-tensor $U = \{ u_{ij} \}$

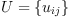
fricas

U:=Σ(Σ(script(u,[[],[i,j]]),dx,i),dx,j)

   There are no library operations named Σ 
      Use HyperDoc Browse or issue
                                 )what op Σ
      to learn if there is any operation containing " Σ " in its name.

   Cannot find a definition or applicable library operation named Σ 
      with argument type(s) 
                                   Symbol
                                Variable(dx)
                                 Variable(i)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Definition 1

We say that the scalar product is associative if the tensor equation holds:

    Y   =   Y
     U     U

In other words, if the (3,0)-tensor:

    i  j  k   i  j  k   i  j  k
     \ | /     \/  /     \  \/
      \|/   =   \ /   -   \ /
       0         0         0

$\label{eq7} \Phi = \{ \phi^{ijk} = {y^e}_{ij} u_{ek} - u_{ie} {y_e}^{jk} \}$

(7)

(three-point function) is zero.

fricas

YU := (Y,I)/U - (I,Y)/U

   There are 11 exposed and 15 unexposed library operations named / 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op /
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named / 
      with argument type(s) 
                      Tuple(OrderedVariableList([Y,I]))
                                 Variable(U)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Definition 2

An algebra with a non-degenerate associative scalar product is called pre-Frobenius.

We may consider the problem where multiplication Y is given, and look for all associative scalar products 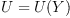or we may consider an scalar product U as given, and look for all algebras 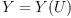such that the scalar product is associative.

This problem can be solved using linear algebra.

fricas

)expose MCALCFN

   MultiVariableCalculusFunctions is now explicitly exposed in frame 
      initial 
K := jacobian(ravel(YU),concat(map(variables,ravel(Y)))::List Symbol);

   There are 1 exposed and 0 unexposed library operations named ravel 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op ravel
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named ravel
      with argument type(s) 
                                Variable(YU)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

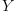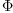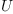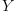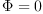The matrix K transforms the coefficients of the tensor into coefficients of the tensor $\Phi$ . We are looking for coefficients of the tensor such that K transforms the tensor into $\Phi=0$ for any .

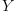A necessary condition for the equation to have a non-trivial solution is that the matrix K be degenerate.

Theorem 1

All 2-dimensional pre-Frobenius algebras are symmetric.

Proof: Consider the determinant of the matrix K above.

fricas

Kd := factor(determinant(K)::DMP(concat map(variables,ravel(U)),FRAC INT))

   There are 1 exposed and 0 unexposed library operations named ravel 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op ravel
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named ravel
      with argument type(s) 
                                 Variable(U)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

The scalar product must also be non-degenerate

fricas

Ud:DMP(concat map(variables,ravel(U)),FRAC INT) := determinant [[retract((Dx.i,Dx.j)/U) for j in 1..#Dx] for i in 1..#Dx]

   There are 1 exposed and 0 unexposed library operations named ravel 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op ravel
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named ravel
      with argument type(s) 
                                 Variable(U)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

therefore U must be symmetric.

fricas

nthFactor(Kd,1)

   There are no exposed library operations named nthFactor but there 
      are 3 unexposed operations with that name. Use HyperDoc Browse or
      issue
                            )display op nthFactor
      to learn more about the available operations.

   Cannot find a definition or applicable library operation named 
      nthFactor with argument type(s) 
                                Variable(Kd)
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Theorem 2

All 2-dimensional algebras with associative scalar product are commutative.

Proof: The basis of the null space of the symmetric K matrix are all symmetric

fricas

YUS := (I,Y)/US - (Y,I)/US

   There are 11 exposed and 15 unexposed library operations named / 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op /
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named / 
      with argument type(s) 
                      Tuple(OrderedVariableList([I,Y]))
                                Variable(US)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

This defines a 4-parameter family of 2-d pre-Frobenius algebras

fricas

test(eval(YUS,SS)=0*YUS)

   There are 10 exposed and 6 unexposed library operations named eval 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op eval
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named eval 
      with argument type(s) 
                                Variable(YUS)
                                Variable(SS)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Alternatively we may consider

fricas

J := jacobian(ravel(YU),concat(map(variables,ravel(U)))::List Symbol);

   There are 1 exposed and 0 unexposed library operations named ravel 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op ravel
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named ravel
      with argument type(s) 
                                Variable(YU)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

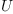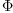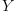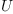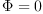The matrix J transforms the coefficients of the tensor into coefficients of the tensor $\Phi$ . We are looking for coefficients of the tensor such that J transforms the tensor into $\Phi=0$ for any .

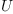A necessary condition for the equation to have a non-trivial solution is that all 70 of the 4x4 sub-matrices of J are degenerate. To this end we can form the polynomial ideal of the determinants of these sub-matrices.

fricas

JP:=ideal concat concat concat
  [[[[ determinant(
    matrix([row(J,i1),row(J,i2),row(J,i3),row(J,i4)]))::FRAC POLY INT
      for i4 in (i3+1)..maxRowIndex(J) ] 
        for i3 in (i2+1)..(maxRowIndex(J)-1) ]
          for i2 in (i1+1)..(maxRowIndex(J)-2) ]
            for i1 in minRowIndex(J)..(maxRowIndex(J)-3) ];

   There are 2 exposed and 0 unexposed library operations named 
      minRowIndex having 1 argument(s) but none was determined to be 
      applicable. Use HyperDoc Browse, or issue
                           )display op minRowIndex
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named 
      minRowIndex with argument type(s) 
                                 Variable(J)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Theorem 3

If a 2-d algebra is associative, commutative, anti-commutative or if it satisfies the Jacobi identity then it is a pre-Frobenius algebra.

Proof

Consider the ideals of the associator, commutator, anti-commutator and Jacobi identity

fricas

YYI:=ideal(ravel(YY)::List FRAC POLY INT);

   There are 1 exposed and 0 unexposed library operations named ravel 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op ravel
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named ravel
      with argument type(s) 
                                Variable(YY)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Y-forms

Three traces of two graftings of an algebra gives six (2,0)-forms.

Left snail and right snail:

  LS                    RS

  Y /\                    /\ Y
   Y  )                  (  Y
    \/                    \/

  i  j                        j  i
   \/                          \/
    \    /\              /\    /
     e  f  \            /  f  e
      \/    \          /    \/
       \    /          \    /
        f  /            \  f
         \/              \/

$\label{eq8} LS = \{ {y^e}_{ij} {y^f}_{ef} \} \ RS = \{ {y^f}_{fe} {y^e}_{ji} \}$

(8)

fricas

LS:=
  ( Y Λ  )/ _
  (  Y I )/ _
      V

   There are no exposed library operations named Y but there are 2 
      unexposed operations with that name. Use HyperDoc Browse or issue
                                )display op Y
      to learn more about the available operations.

   Cannot find a definition or applicable library operation named Y 
      with argument type(s) 
                                 Variable(Λ)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Left and right deer:

   RD                 LD

   \ /\/              \/\ /
    Y /\              /\ Y
     Y  )            (  Y
      \/              \/

   i            j    i            j
    \    /\    /      \    /\    /
     \  f  \  /        \  /  f  /
      \/    \/          \/    \/
       \    /\          /\    /
        e  /  \        /  \  e
         \/    \      /    \/
          \    /      \    /
           f  /        \  f
            \/          \/

$\label{eq9} RD = \{ {y^e}_{if} {y^f}_{ej} \} \ LD = \{ {y^f}_{ie} {y^e}_{fj} \}$

(9)

Left and right deer forms are identical but different from snails.

fricas

RD:=
  (  I Λ I  ) / _
  (   Y X   ) / _
  (    Y I  ) / _
        V

   There are no library operations named Λ 
      Use HyperDoc Browse or issue
                                 )what op Λ
      to learn if there is any operation containing " Λ " in its name.

   Cannot find a definition or applicable library operation named Λ 
      with argument type(s) 
                                 Variable(I)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Left and right turtles:

  RT                   LT

   /\ / /               \ \ /\
  (  Y /                 \ Y  )
   \  Y                   Y  /
    \/                     \/

           i     j      i     j
    /\    /     /        \     \    /\
   /  f  /     /          \     \  f  \
  /    \/     /            \     \/    \
  \     \    /              \    /     /
   \     e  /                \  e     /
    \     \/                  \/     /
     \    /                    \    /
      \  f                      f  /
       \/                        \/

$\label{eq10} RT = \{ {y^e}_{fi} {y^f}_{ej} \} \ LT = \{ {y^f}_{ie} {y^e}_{jf} \}$

(10)

fricas

RT:=
  (  Λ I I ) / _
  ( I Y I  ) / _
  (  I Y   ) / _
      V

   There are no exposed library operations named I but there is one 
      unexposed operation with that name. Use HyperDoc Browse or issue
                                )display op I
      to learn more about the available operation.

   Cannot find a definition or applicable library operation named I 
      with argument type(s) 
                                 Variable(I)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

The turles are symmetric

fricas

test(RT = X/RT)

$\label{eq11} \mbox{\rm false}$

(11)

Type: Boolean

fricas

test(LT = X/LT)

$\label{eq12} \mbox{\rm false}$

(12)

Type: Boolean

Five of the six forms are independent.

fricas

test(RT=RS)

$\label{eq13} \mbox{\rm false}$

(13)

Type: Boolean

fricas

test(RT=LS)

$\label{eq14} \mbox{\rm false}$

(14)

Type: Boolean

fricas

test(RT=RD)

$\label{eq15} \mbox{\rm false}$

(15)

Type: Boolean

fricas

test(LT=RS)

$\label{eq16} \mbox{\rm false}$

(16)

Type: Boolean

fricas

test(LT=LS)

$\label{eq17} \mbox{\rm false}$

(17)

Type: Boolean

fricas

test(LT=RD)

$\label{eq18} \mbox{\rm false}$

(18)

Type: Boolean

Associativity implies right turtle equals right snail and left turtle equals left snail.

fricas

in?(ideal(ravel(RT-RS)::List FRAC POLY INT),YYI)

   There are 1 exposed and 0 unexposed library operations named ravel 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op ravel
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named ravel
      with argument type(s) 
                             Polynomial(Integer)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

If the Jacobi identity holds then both snails are zero

fricas

in?(ideal(ravel(RS)::List FRAC POLY INT),YXI)

   There are 1 exposed and 0 unexposed library operations named ravel 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op ravel
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named ravel
      with argument type(s) 
                                Variable(RS)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

and right turtle and deer have opposite signs

fricas

in?(ideal(ravel(RT+RD)::List FRAC POLY INT),YXI)

   There are 1 exposed and 0 unexposed library operations named ravel 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op ravel
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named ravel
      with argument type(s) 
                             Polynomial(Integer)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Subject: Be Bold !!

	( 15 subscribers )