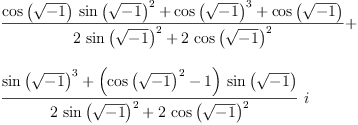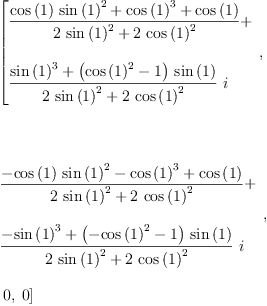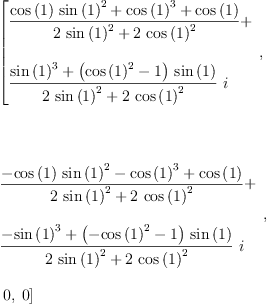MathAction SandBoxBiQuaternions2

Topics

FrontPage
- SandBox
  - SandBoxBiQuaternions
    - SandBoxBiQuaternions2 <-- You are here.

SandBoxBiQuaternions3

Biquaternion Calculus Domain

D. Cyganski and Bill Page - July 2007

This version is implemented as a new domain in Aldor .

fricas

(1) -> <aldor>
#pile
#include "fricas"

import from NonNegativeInteger

BiQuaternion(R:Join(OrderedSet,CommutativeRing)): Exports == Implementation where
  C==>Complex Expression R
  Exports ==> QuaternionCategory(C) with
    qlist: List C -> %
    -- takes a complex list (parameter l) into a quaternion
    listq: % -> List C
    -- takes a quaternion into a list
    matrixq: % -> SquareMatrix(2,C)
    -- takes a quaternion into a matrix
    sig0:%
    sig1:%
    sig2:%
    sig3:%
    siglist: % -> List C
    -- Pauli basis representation of the biquaternion
    if Complex(Expression(R)) has PartialDifferentialRing(Symbol) then
      D: (%,Symbol,Symbol,Symbol) -> %
    -- quaternion derivative
    rot: (C,%) -> %
    -- biquaternion rotation
    /: (%,%) -> %
    /: (C,%) -> %
    /: (%,C) -> %
    abs: % -> C
    exp: % -> %
    coerce: Complex R -> %

  Implementation ==> Quaternion C add
    import from C

    coerce(z:Complex R):% ==
      import from Expression(R),ComplexFunctions2(R,Expression R)
      map(coerce,z)::%

    -- Define a function that takes a complex list (parameter l) into a quaternion
    qlist(l:List C):%==
      import from Integer
      quatern(l 1,l 2,l 3,l 4)
    -- Define a function that takes a quaternion into a list
    listq(x:%):List C == [real x, imagI x, imagJ x, imagK x]
    -- Define a function that takes a biquat into a matrix
    matrixq(x:%):SquareMatrix(2,C) ==
       import from List List C
       matrix [[real x + imaginary()*imagI(x), imagJ x + imaginary()*imagK(x)],
               [-imagJ(x) + imaginary()*imagK(x), real x - imaginary()*imagI(x)]]
    -- Define a function that produces the Pauli basis representation of the biquaternion
    siglist(x:%):List C == [real x, -imaginary()*imagK(x),-imaginary()*imagJ(x),imaginary()*imagI(x)]
    sig0:% == quatern(1,0,0,0)
    sig1:% == imaginary() * quatern(0,0,0,1)
    sig2:% == imaginary() * quatern(0,0,1,0)
    sig3:% == -imaginary() * quatern(0,1,0,0)
    -- Define the quaternion derivative (Morgan, 2001, Eq. 2)
    if Complex(Expression(R)) has PartialDifferentialRing(Symbol) then
      D(q:%,x:Symbol,y:Symbol,z:Symbol):% == sig1*D(q,x)+sig2*D(q,y)+sig3*D(q,z)
    -- Define a biquaternion rotation operator that takes a biquat through a rotation
    -- of theta radians about the axis defined by the unit q biquat (Morgan 2001, Eq 3).
    rot(theta:C,q:%):% ==
      import from Integer, SparseMultivariatePolynomial(Integer, Kernel(C))
      cos(theta/2::C)::% - imaginary()*q*sin(theta/2::C)
    ((x:%)/(y:%)):% == x*inv(y)
    ((x:C)/(y:%)):% == (x::%)*inv(y)
    ((x:%)/(y:C)):% == x*inv(y::%)
    abs(q:%):C ==
      sqrt(retract(q*conjugate(q)))
    exp(q:%):% ==
      import from Integer, SparseMultivariatePolynomial(Integer, Kernel(C))
      q-conjugate(q)=0 => exp(retract(q+conjugate(q))/2::C)*sig0
      exp(retract(q+conjugate(q))/2::C) * (sig0*cos(abs(q)) + (q-conjugate(q))/abs(q-conjugate(q)) * sin(abs(q)))</aldor>

fricas

Compiling FriCAS source code from file 
      /var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/8265291018112466544-25px001.as
      using Aldor compiler and options 
-O -Fasy -Fao -Flsp -lfricas -Mno-ALDOR_W_WillObsolete -DFriCAS -Y $FRICAS/algebra -I $FRICAS/algebra
      Use the system command )set compiler args to change these 
      options.

fricas

Compiling Lisp source code from file 
      ./8265291018112466544-25px001.lsp
   Issuing )library command for 8265291018112466544-25px001

fricas

Reading /var/aw/var/LatexWiki/8265291018112466544-25px001.asy
   BiQuaternion is now explicitly exposed in frame initial 
   BiQuaternion will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/8265291018112466544-25px001

fricas

)show BiQuaternion

 BiQuaternion(R: Join(OrderedSet,CommutativeRing)) is a domain constructor
 Abbreviation for BiQuaternion is BIQUAT 
 This constructor is exposed in this frame.
------------------------------- Operations --------------------------------

 0 : () -> %                           1 : () -> %
 sample : () -> %                      sig0 : () -> %
 sig1 : () -> %                        sig2 : () -> %
 sig3 : () -> %                       
 ?*? : (%, Integer) -> % if Complex(Expression(R)) has LINEXP(INT)
 ?*? : (%, Fraction(Integer)) -> % if Complex(Expression(R)) has FIELD
 ?*? : (Fraction(Integer), %) -> % if Complex(Expression(R)) has FIELD
 ?<=? : (%, %) -> Boolean if Complex(Expression(R)) has ORDSET
 ?>? : (%, %) -> Boolean if Complex(Expression(R)) has ORDSET
 ?>=? : (%, %) -> Boolean if Complex(Expression(R)) has ORDSET
 D : % -> % if Complex(Expression(R)) has DIFRING
 D : (%, NonNegativeInteger) -> % if Complex(Expression(R)) has DIFRING
 D : (%, Symbol) -> % if Complex(Expression(R)) has PDRING(SYMBOL)
 D : (%, List(Symbol)) -> % if Complex(Expression(R)) has PDRING(SYMBOL)
 D : (%, Symbol, NonNegativeInteger) -> % if Complex(Expression(R)) has PDRING(SYMBOL)
 D : (%, List(Symbol), List(NonNegativeInteger)) -> % if Complex(Expression(R)) has PDRING(SYMBOL)
 D : (%, Symbol, Symbol, Symbol) -> % if Complex(Expression(R)) has PDRING(SYMBOL)
 ?^? : (%, Integer) -> % if Complex(Expression(R)) has FIELD
 associates? : (%, %) -> Boolean if Complex(Expression(R)) has ENTIRER
 associates? : (%, %) -> Boolean if Complex(Expression(R)) has FIELD
 charthRoot : % -> Union(value1: %,failed: Enumeration(failed)) if Complex(Expression(R)) has CHARNZ
 differentiate : (%, NonNegativeInteger) -> % if Complex(Expression(R)) has DIFRING
 differentiate : (%, List(Symbol)) -> % if Complex(Expression(R)) has PDRING(SYMBOL)
 differentiate : (%, Symbol, NonNegativeInteger) -> % if Complex(Expression(R)) has PDRING(SYMBOL)
 differentiate : (%, List(Symbol), List(NonNegativeInteger)) -> % if Complex(Expression(R)) has PDRING(SYMBOL)
 eval : (%, Complex(Expression(R)), Complex(Expression(R))) -> % if Complex(Expression(R)) has EVALAB(COMPLEX(EXPR(R)))
 eval : (%, List(Complex(Expression(R))), List(Complex(Expression(R)))) -> % if Complex(Expression(R)) has EVALAB(COMPLEX(EXPR(R)))
 eval : (%, Equation(Complex(Expression(R)))) -> % if Complex(Expression(R)) has EVALAB(COMPLEX(EXPR(R)))
 eval : (%, Symbol, Complex(Expression(R))) -> % if Complex(Expression(R)) has IEVALAB(SYMBOL,COMPLEX(EXPR(R)))
 exquo : (%, %) -> Union(value1: %,failed: Enumeration(failed)) if Complex(Expression(R)) has ENTIRER
 exquo : (%, %) -> Union(value1: %,failed: Enumeration(failed)) if Complex(Expression(R)) has FIELD
 max : (%, %) -> % if Complex(Expression(R)) has ORDSET
 min : (%, %) -> % if Complex(Expression(R)) has ORDSET
 smaller? : (%, %) -> Boolean if Complex(Expression(R)) has ORDSET
 unit? : % -> Boolean if Complex(Expression(R)) has ENTIRER
 unit? : % -> Boolean if Complex(Expression(R)) has FIELD
 unitCanonical : % -> % if Complex(Expression(R)) has ENTIRER
 unitCanonical : % -> % if Complex(Expression(R)) has FIELD
 unitNormal : % -> Record(unit: %,canonical: %,associate: %) if Complex(Expression(R)) has ENTIRER
 unitNormal : % -> Record(unit: %,canonical: %,associate: %) if Complex(Expression(R)) has FIELD

fricas

Q := BiQuaternion Integer

$\label{eq1}\hbox{\axiomType{BiQuaternion}\ } \left({\hbox{\axiomType{Integer}\ }}\right)$

(1)

Type: Type

fricas

q:Q := quatern(q0,q1,q2,q3)

$\label{eq2}q 0 +{q 1 \ i}+{q 2 \ j}+{q 3 \ k}$

(2)

Type: BiQuaternion?(Integer)

For testing the derivative we define this set of operators

fricas

Ft:=operator 'Ft; Fx:=operator 'Fx; Fy:=operator 'Fy; Fz:=operator 'Fz;

Type: BasicOperator?

Now form a general quaternion which is a function of x,y,z

fricas

F:Q:=Ft(x,y,z)*sig0()+Fx(x,y,z)*sig1()+Fy(x,y,z)*sig2()+Fz(x,y,z)*sig3()

$\label{eq3}{Ft \left({x , \: y , \: z}\right)}-{{Fz \left({x , \: y , \: z}\right)}\ i \ i}+{{Fy \left({x , \: y , \: z}\right)}\ i \ j}+{{Fx \left({x , \: y , \: z}\right)}\ i \ k}$

(3)

Type: BiQuaternion?(Integer)

In the Pauli basis the derivative of this biquat should produce (Morgan 2001, eq 1):

  D(Ft+F.sigma)=div(F)+(grad(Ft)+%i*curl(F)).sigma

which it does

fricas

siglist(D(F,x,y,z))

$\label{eq4}\begin{array}{@{}l} \displaystyle \left[{{{Fz_{, 3}}\left({x , \: y , \: z}\right)}+{{Fy_{, 2}}\left({x , \: y , \: z}\right)}+{{Fx_{, 1}}\left({x , \: y , \: z}\right)}}, \: \right. \ \ \displaystyle \left.{{{Ft_{, 1}}\left({x , \: y , \: z}\right)}+{{\left({{Fz_{, 2}}\left({x , \: y , \: z}\right)}-{{Fy_{, 3}}\left({x , \: y , \: z}\right)}\right)}\ i}}, \: \right. \ \ \displaystyle \left.{{{Ft_{, 2}}\left({x , \: y , \: z}\right)}+{{\left(-{{Fz_{, 1}}\left({x , \: y , \: z}\right)}+{{Fx_{, 3}}\left({x , \: y , \: z}\right)}\right)}\ i}}, \: \right. \ \ \displaystyle \left.{{{Ft_{, 3}}\left({x , \: y , \: z}\right)}+{{\left({{Fy_{, 1}}\left({x , \: y , \: z}\right)}-{{Fx_{, 2}}\left({x , \: y , \: z}\right)}\right)}\ i}}\right]$

(4)

Type: List(Complex(Expression(Integer)))

Test

(comment out this test later)

fricas

%i::Q

$\label{eq5}i$

(5)

Type: BiQuaternion?(Integer)

fricas

abs(%i::Q)

$\label{eq6}\sqrt{- 1}$

(6)

Type: Complex(Expression(Integer))

fricas

abs(q)

$\label{eq7}\sqrt{{{q 3}^{2}}+{{q 2}^{2}}+{{q 1}^{2}}+{{q 0}^{2}}}$

(7)

Type: Complex(Expression(Integer))

fricas

cos(abs(%i::Q))

$\label{eq8}\begin{array}{@{}l} \displaystyle {\frac{{{\cos \left({\sqrt{- 1}}\right)}\ {{\sin \left({\sqrt{- 1}}\right)}^{2}}}+{{\cos \left({\sqrt{- 1}}\right)}^{3}}+{\cos \left({\sqrt{- 1}}\right)}}{{2 \ {{\sin \left({\sqrt{- 1}}\right)}^{2}}}+{2 \ {{\cos \left({\sqrt{- 1}}\right)}^{2}}}}}+ \ \ \displaystyle {{\frac{{{\sin \left({\sqrt{- 1}}\right)}^{3}}+{{\left({{\cos \left({\sqrt{- 1}}\right)}^{2}}- 1 \right)}\ {\sin \left({\sqrt{- 1}}\right)}}}{{2 \ {{\sin \left({\sqrt{- 1}}\right)}^{2}}}+{2 \ {{\cos \left({\sqrt{- 1}}\right)}^{2}}}}}\ i}$

(8)

Type: Complex(Expression(Integer))

If I've defined these correctly, then the rotation about the x axis defined by qx below by 2 radians should give the same answer as exponentiation to -%i*qx (not a very complete test)

fricas

qx:Q:=sig1()

$\label{eq9}i \ k$

(9)

Type: BiQuaternion?(Integer)

fricas

siglist(rot(2,qx))

$\label{eq10}\begin{array}{@{}l} \displaystyle \left[{ \begin{array}{@{}l} \displaystyle {\frac{{{\cos \left({1}\right)}\ {{\sin \left({1}\right)}^{2}}}+{{\cos \left({1}\right)}^{3}}+{\cos \left({1}\right)}}{{2 \ {{\sin \left({1}\right)}^{2}}}+{2 \ {{\cos \left({1}\right)}^{2}}}}}+ \ \ \displaystyle {{\frac{{{\sin \left({1}\right)}^{3}}+{{\left({{\cos \left({1}\right)}^{2}}- 1 \right)}\ {\sin \left({1}\right)}}}{{2 \ {{\sin \left({1}\right)}^{2}}}+{2 \ {{\cos \left({1}\right)}^{2}}}}}\ i}$

(10)

Type: List(Complex(Expression(Integer)))

fricas

siglist(exp(-%i::Q*qx))

$\label{eq11}\begin{array}{@{}l} \displaystyle \left[{ \begin{array}{@{}l} \displaystyle {\frac{{{\cos \left({1}\right)}\ {{\sin \left({1}\right)}^{2}}}+{{\cos \left({1}\right)}^{3}}+{\cos \left({1}\right)}}{{2 \ {{\sin \left({1}\right)}^{2}}}+{2 \ {{\cos \left({1}\right)}^{2}}}}}+ \ \ \displaystyle {{\frac{{{\sin \left({1}\right)}^{3}}+{{\left({{\cos \left({1}\right)}^{2}}- 1 \right)}\ {\sin \left({1}\right)}}}{{2 \ {{\sin \left({1}\right)}^{2}}}+{2 \ {{\cos \left({1}\right)}^{2}}}}}\ i}$

(11)

Type: List(Complex(Expression(Integer)))

which it does

fricas

(%%(-1)=%%(-2))@Boolean

$\label{eq12} \mbox{\rm true}$

(12)

Type: Boolean

I would love to express a proof of equality such as:

   rot(theta,q) = exp((-theta/2)*%i*q)

for arbitrary real 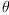$\theta$ and biquaternion q as I would in Maple.

fricas

theta:Complex Expression Integer := _\theta

$\label{eq13}\theta$

(13)

Type: Complex(Expression(Integer))

fricas

map(simplify, siglist( rot(theta,q) - exp((-%i*theta/2) * q)))::List Expression Complex Integer

$\label{eq14}\begin{array}{@{}l} \displaystyle \left[{ \begin{array}{@{}l} \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle {i \ {\sin \left({\frac{\theta \ q 0}{2}}\right)}}- \ \ \displaystyle {\cos \left({\frac{\theta \ q 0}{2}}\right)}$

(14)

Type: List(Expression(Complex(Integer)))

fricas

map(simplify,siglist(rot(2,qx)))::List Expression Complex Integer

$\label{eq15}\left[{\cos \left({1}\right)}, \: -{i \ {\sin \left({1}\right)}}, \: 0, \: 0 \right]$

(15)

Type: List(Expression(Complex(Integer)))

Subject: Be Bold !!

	( 15 subscribers )