The Biquaternion calculus support function collection D. Cyganski - May-June 2007 Hamiltonian BiquaternionsDefine the type Q of Hamiltonian biquaternions (not to be confused with Clifford biquaternions which are an entirely different object) fricas (1) -> C:=Complex Expression Integer
Type: Type
fricas Q:=Quaternion C
Type: Type
fricas q:Q:=quatern(q0,
Type: Quaternion(Complex(Expression(Integer)))
Define a function that takes a complex list (parameter l) into a quaternion fricas qlist(l:List C):Q==quatern(l.1, Type: Void
Define a function that takes a quaternion into a list fricas listq(x:Q):List C == [real x, Type: Void
Define a function that takes a biquat into a matrix fricas matrixq(x:Q):Matrix C == matrix _
[[real x + %i*imagI(x),
Type: Void
The Pauli basis BiquaternionsThe quaternion package in axiom is based upon the Hamiltonian basis, i,j,k, in constrast to the Pauli basis used in the Mogan papers which make certain operations correspond more closely (in the sense of visualization as ordering of components is more natural so that classical operations can be easily identified) to vector calculus functions and connect with more directly with various spinor QM formulations. To both follow these papers and obtain these visualization benefits, we will define and use the Pauli basis also. The Pauli basis in terms of the Hamiltonian quaternion basis fricas sig0:=quatern(1,
Type: Quaternion(Complex(Expression(Integer)))
fricas sig1:=%i*quatern(0,
Type: Quaternion(Complex(Expression(Integer)))
fricas sig2:=%i*quatern(0,
Type: Quaternion(Complex(Expression(Integer)))
fricas sig3:=-%i*quatern(0,
Type: Quaternion(Complex(Expression(Integer)))
For purposes of manipulation and display it would be best if we either:
While 2. is not as natural and convenient, it is easier to code and would automatically provide a development that could be seen in the visually appealing Pauli form, or in the standard Hamiltonian form of biquaternions. After a quick review and finding no fast path to 2. and not wishing to get into the mechanics of compiling an axiom package instead of working on the physics, I have taken the yet easier path and simply defined the simplest display function that gives me access to seeing Pauli basis results: a list of the the four Pauli basis coefficients. Define a function that produces the Pauli basis representation of the biquaternion fricas siglist(x:Q):List C == _ [real x, Type: Void
Biquaternion CalculusDefine the quaternion derivative (Morgan, 2001, Eq. 2) fricas D(q:Q, Type: Void
For testing the derivative we define this set of operators fricas Ft:=operator 'Ft; Fx:=operator 'Fx; Fy:=operator 'Fy; Fz:=operator 'Fz; Type: BasicOperator?
Now form a general quaternion which is a function of x,y,z fricas F:Q:=Ft(x,
Type: Quaternion(Complex(Expression(Integer)))
In the Pauli basis the derivative of this biquat should produce (Morgan 2001, eq 1): D(Ft+F.sigma)=div(F)+(grad(Ft)+%i*curl(F)).sigma which it does fricas siglist(D(F, fricas Compiling function D with type (Quaternion(Complex(Expression(
Integer))),fricas Compiling function siglist with type Quaternion(Complex(Expression(
Integer))) -> List(Complex(Expression(Integer)))
Type: List(Complex(Expression(Integer)))
Biquaternion ExponentialDefine a function that evaluates the Biquat exponential by beginning with the biquat rotation First let's introduce some refinement to the language we will use. In many
texts and papers, the i,j,k or sigma1, sigma2, sigma3 components of the
biquaternion are called the imaginary components while the scalar or sigma0
component are called real. This introduces vast confusion when dealing with
biquaternions in which there is a "true" imaginary unit, %i being used. We
will adopt a variation on the language used by Gsponer and others. A biquat
[0,b,c,d]=[0,Re(b),Re(c),Re(d)]+[0,Im(b),Im(c),Im(d)]=Re(Vec(q))+Im(Vec(q)) Thus, for us, a "real quaternion" has real scalar and vector components and does not refer to a quaternion with only a scalar component as it would in the language adopted by the quatern package in axiom. The rotation is a function of real number, theta and a unit norm, real vector quaternion. It's form is that of a simple complex quaternion exponential, R(theta,q) = exp(a) where a is an Imaginary Vector quaternion. The result is Unit Norm, Vector quaternion. That is, exponentials of pure imaginary, pure vector quaternions are like exponentials of pure imaginary numbers, resulting in each case in a unit norm object of the same type. For many of our purposes in the representation of relativistic and quantum mechanics it is the only type of quaternion for which we will have to evaluate the exponential. Define a biquaternion rotation operator that takes a biquat through a rotation of theta radians about the axis defined by the unit q biquat (Morgan 2001, Eq 3). fricas rot(theta:Expression Integer, Type: Void
The rotation is a basis for defining the general exponential, since we can always extract the unit vector corresponding to a given biquaternion, all we need is the biquaternion abs operation, not provided by axiom (note, many texts and papers label the abs which is a complex valued norm^2 by the name "norm" - very bad form -- I've adopted abs as the name to avoid this confusion. fricas ((x:Q)/(y:Q)):Q == x*inv(y) Type: Void
fricas abs(q:Q):C == sqrt((q*conjugate(q))::C) Type: Void
fricas exp(q:Q):Q == ( _ q-conjugate(q)=0 => exp( (q+conjugate(q))::C/2)$C * sig0; _ exp( (q+conjugate(q))::C/2)$C * (sig0*cos(abs(q)) + (q-conjugate(q))/abs(q-conjugate(q))*sin(abs(q))) ) Type: Void
Test (comment out this test later) If I've defined these correctly, then the rotation about the x axis defined by qx below by 2 radians
should give the same answer as exponentiation to fricas qx:=sig1
Type: Quaternion(Complex(Expression(Integer)))
fricas siglist(rot(2, fricas Compiling function / with type (Quaternion(Complex(Expression(
Integer))),fricas Compiling function rot with type (Expression(Integer),
Type: List(Complex(Expression(Integer)))
fricas siglist(exp(-%i::Q*qx)) fricas Compiling function exp with type Quaternion(Complex(Expression(
Integer))) -> Quaternion(Complex(Expression(Integer)))fricas Compiling function abs with type Quaternion(Complex(Expression(
Integer))) -> Complex(Expression(Integer))
Type: List(Complex(Expression(Integer)))
which it does fricas (%%(-1)=%%(-2))@Boolean
Type: Boolean
To express a proof of equality such as: rot(theta,q) = exp((-theta/2)*%i*q) for arbitrary real fricas qnv:=q1*sig1+q2*sig2+sqrt(1-q1^2-q2^2)*sig3
Type: Quaternion(Complex(Expression(Integer)))
Assumptions about Variables Now, in the equations that will result, we will obtain subexpressions of the form
ProblemsReturning to the case at hand, let's expand a test of equality of the four biquat components and seek a way to prove that each component is zero. fricas theta := _\theta
Type: Variable(\theta)
fricas testqeq:=map(simplify,
Type: List(Expression(Complex(Integer)))
As is quite obvious from this result, the two equations would have been shown to be equal if positivity of the theta variable was enforced. This raises two questions: (1) How would one perform a proof such as the above within the allowed operations of Axiom? (2) How can Axiom be called an symbolic algebra system if basic notions of algebraic proof such as restrictions of a variable to the semiring of non-negative integers is disallowed? How are symbolic manipulations, proofs and solutions to be carried out without this basic notion? I am led to think that axiom can only be considered a semi-numerical software system. Rules and Pattern MatchingLet's try another way to answer question 1 by using symbolic pattern matching "rules". Define a rule that recognizes the specific case of the variable theta appearing in a construct that should be simplified given its positivity fricas posthetaRule:=rule sqrt(theta^2)==theta
But, now we encounter two new problems... a) Apparently "map" does not work with rules, so I can't apply this rule in a simple fashion to the entire List generated by our test case above for any x.
fricas map(x+->posthetaRule(x),
Type: List(Expression(Integer))
b) But even if we were to split our list above, and try to apply this rule to a component, we get this disappointing result fricas posthetaRule testqeq.1 Apparently rules have built in assumption about the construction of the expression If I override this for a real element of the list we are testing I can successfully get one answer fricas [posthetaRule (testqeq.i::Expression Integer) for i in 1..1]
Type: List(Expression(Integer))
But this doesn't extend to the remainder of the list fricas [posthetaRule (testqeq.i::Expression Integer) for i in 1..4] because obviously we can't coerce an actually complex value into the Expression Integer type that the rule seems to want. Here is one way to create the necessary rule. Like everything else in Axiom rules are objects in some domain. We need to specify a domain for the rule that is compatible with the domain we wish to manipulate. So let's find out more about this domain: fricas )show RewriteRule We can provide satisfactory parameters of this domain constructor as follows: fricas Complex Integer has PatternMatchable Integer
Type: Boolean
fricas Expression Complex Integer has FunctionSpace Complex Integer
Type: Boolean
fricas Expression Complex Integer has PatternMatchable Integer
Type: Boolean
So the following simplification works as hoped: fricas posxRule:=(rule sqrt('theta^2)==theta)$RewriteRule(Integer,
fricas map(x+->posxRule x,
Type: List(Expression(Complex(Integer)))
Algebraic Domain of ComputationRecall that Axiom does things in an fundamentally algebraic rather than symbolic way. So although the pattern matching approach works, it goes somewhat against the overall philosophy of Axiom. It is possible to do almost anything by using rewrite rules including things that are mathematically incorrect. In this case the rule is simple and the results obvious but it more complicated situations this can be a problem. Is there some "axiomatic", i.e. algebraic way to express the fact that be satisfied. Now consider that by definition of fricas test (sqrt(x)^2=x)
Type: Boolean
and so fricas test (sqrt(sqrt(x)^2)=sqrt(x))
Type: Boolean
for any x. So the expression fricas eval(eval(testqeq ,
Type: List(Expression(Complex(Integer)))
See OverloadProblems for some interesting observations and problems that resulted from further development of this work with regard to type conversions and function overloading |
|
|
|
last edited 3 years ago by test1 |
![\label{eq9}\begin{array}{@{}l}
\displaystyle
\left[{{{Fz_{, 3}}\left({x , \: y , \: z}\right)}+{{Fy_{, 2}}\left({x , \: y , \: z}\right)}+{{Fx_{, 1}}\left({x , \: y , \: z}\right)}}, \: \right.
\
\
\displaystyle
\left.{{{Ft_{, 1}}\left({x , \: y , \: z}\right)}+{{\left({{Fz_{, 2}}\left({x , \: y , \: z}\right)}-{{Fy_{, 3}}\left({x , \: y , \: z}\right)}\right)}\ i}}, \: \right.
\
\
\displaystyle
\left.{{{Ft_{, 2}}\left({x , \: y , \: z}\right)}+{{\left(-{{Fz_{, 1}}\left({x , \: y , \: z}\right)}+{{Fx_{, 3}}\left({x , \: y , \: z}\right)}\right)}\ i}}, \: \right.
\
\
\displaystyle
\left.{{{Ft_{, 3}}\left({x , \: y , \: z}\right)}+{{\left({{Fy_{, 1}}\left({x , \: y , \: z}\right)}-{{Fx_{, 2}}\left({x , \: y , \: z}\right)}\right)}\ i}}\right]
\label{eq9}\begin{array}{@{}l}
\displaystyle
\left[{{{Fz_{, 3}}\left({x , \: y , \: z}\right)}+{{Fy_{, 2}}\left({x , \: y , \: z}\right)}+{{Fx_{, 1}}\left({x , \: y , \: z}\right)}}, \: \right.
\
\
\displaystyle
\left.{{{Ft_{, 1}}\left({x , \: y , \: z}\right)}+{{\left({{Fz_{, 2}}\left({x , \: y , \: z}\right)}-{{Fy_{, 3}}\left({x , \: y , \: z}\right)}\right)}\ i}}, \: \right.
\
\
\displaystyle
\left.{{{Ft_{, 2}}\left({x , \: y , \: z}\right)}+{{\left(-{{Fz_{, 1}}\left({x , \: y , \: z}\right)}+{{Fx_{, 3}}\left({x , \: y , \: z}\right)}\right)}\ i}}, \: \right.
\
\
\displaystyle
\left.{{{Ft_{, 3}}\left({x , \: y , \: z}\right)}+{{\left({{Fy_{, 1}}\left({x , \: y , \: z}\right)}-{{Fx_{, 2}}\left({x , \: y , \: z}\right)}\right)}\ i}}\right]](images/787526583911745654-16.0px.png)
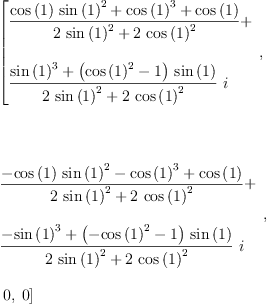
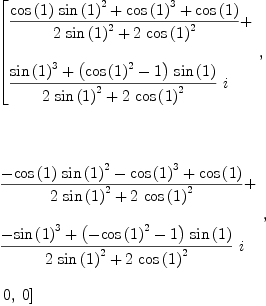
![\label{eq16}\begin{array}{@{}l}
\displaystyle
\left[{-{\cos \left({\frac{\sqrt{{\theta}^{2}}}{2}}\right)}+{\cos \left({\frac{\theta}{2}}\right)}}, \: \right.
\
\
\displaystyle
\left.{\frac{{i \ q 1 \ {\sqrt{{\theta}^{2}}}\ {\sin \left({\frac{\sqrt{{\theta}^{2}}}{2}}\right)}}-{i \ \theta \ q 1 \ {\sin \left({\frac{\theta}{2}}\right)}}}{\theta}}, \right.
\
\
\displaystyle
\left.\: \right.
\
\
\displaystyle
\left.{\frac{{i \ q 2 \ {\sqrt{{\theta}^{2}}}\ {\sin \left({\frac{\sqrt{{\theta}^{2}}}{2}}\right)}}-{i \ \theta \ q 2 \ {\sin \left({\frac{\theta}{2}}\right)}}}{\theta}}, \right.
\
\
\displaystyle
\left.\: \right.
\
\
\displaystyle
\left.{\frac{{i \ {\sqrt{-{{q 2}^{2}}-{{q 1}^{2}}+ 1}}\ {\sqrt{{\theta}^{2}}}\ {\sin \left({\frac{\sqrt{{\theta}^{2}}}{2}}\right)}}-{i \ \theta \ {\sin \left({\frac{\theta}{2}}\right)}\ {\sqrt{-{{q 2}^{2}}-{{q 1}^{2}}+ 1}}}}{\theta}}\right]
\label{eq16}\begin{array}{@{}l}
\displaystyle
\left[{-{\cos \left({\frac{\sqrt{{\theta}^{2}}}{2}}\right)}+{\cos \left({\frac{\theta}{2}}\right)}}, \: \right.
\
\
\displaystyle
\left.{\frac{{i \ q 1 \ {\sqrt{{\theta}^{2}}}\ {\sin \left({\frac{\sqrt{{\theta}^{2}}}{2}}\right)}}-{i \ \theta \ q 1 \ {\sin \left({\frac{\theta}{2}}\right)}}}{\theta}}, \right.
\
\
\displaystyle
\left.\: \right.
\
\
\displaystyle
\left.{\frac{{i \ q 2 \ {\sqrt{{\theta}^{2}}}\ {\sin \left({\frac{\sqrt{{\theta}^{2}}}{2}}\right)}}-{i \ \theta \ q 2 \ {\sin \left({\frac{\theta}{2}}\right)}}}{\theta}}, \right.
\
\
\displaystyle
\left.\: \right.
\
\
\displaystyle
\left.{\frac{{i \ {\sqrt{-{{q 2}^{2}}-{{q 1}^{2}}+ 1}}\ {\sqrt{{\theta}^{2}}}\ {\sin \left({\frac{\sqrt{{\theta}^{2}}}{2}}\right)}}-{i \ \theta \ {\sin \left({\frac{\theta}{2}}\right)}\ {\sqrt{-{{q 2}^{2}}-{{q 1}^{2}}+ 1}}}}{\theta}}\right]](images/8114517558791619618-16.0px.png)