help links subscribe changes refresh edit

	FAQ
	↑	→ Creating New Pages

Common Mistakes

Edit detail for Common Mistakes revision 3 of 3

	1 2 3
Editor: kratt6 Time: 2008/01/03 05:16:26 GMT-8
Note: deindent 12 to make mathaction happy

changed:
-   r:Fraction Integer:=1.544
-   eq1:=90*%pi/180-asin(n*sin(34*%pi/180)/r)=asin(n/r)
-   s:=solve(eq1,n)
-   \end{axiom}
r:Fraction Integer:=1.544
eq1:=90*%pi/180-asin(n*sin(34*%pi/180)/r)=asin(n/r)
s:=solve(eq1,n)
   \end{axiom}

changed:
-   eval(eq1,s.1)::Equation Expression Float
-   eval(eq1,s.2)::Equation Expression Float
-   \end{axiom}
eval(eq1,s.1)::Equation Expression Float
eval(eq1,s.2)::Equation Expression Float
   \end{axiom}

Omitting the {axiom} enviroment
You have to use \begin{axiom} ... \end{axiom} or \begin{reduce} ... \end{reduce} before and after the command like this:
```
    \begin{reduce}
    int(1/(a+z^3), z);
    \end{reduce}
```
Axiom commands do not end with ;
Oh yes, note that for Axiom you don't end the command with ; and the command for integration in Axiom is integrate.
fricas
```
(1) -> integrate(1/(a+z^3), z)
```
$\label{eq1}\frac{-{{\sqrt{3}}\ {\log \left({{{{z}^{2}}\ {{\root{3}\of{{a}^{2}}}^{2}}}-{a \ z \ {\root{3}\of{{a}^{2}}}}+{{a}^{2}}}\right)}}+{2 \ {\sqrt{3}}\ {\log \left({{z \ {\root{3}\of{{a}^{2}}}}+ a}\right)}}+{6 \ {\arctan \left({\frac{{2 \ z \ {\sqrt{3}}\ {\root{3}\of{{a}^{2}}}}-{a \ {\sqrt{3}}}}{3 \ a}}\right)}}}{6 \ {\sqrt{3}}\ {\root{3}\of{{a}^{2}}}}$ (1)

Type: Union(Expression(Integer),...)
Reduce commands must end with a semicolon ;
But it must be there for Reduce.
r^2+r+1;
reduce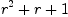
$\displaylines{\qdd r^{2} +r +1 \cr}$
In Axiom ln is written log
This won't work:
```
    \begin{axiom}integrate((x^2+2*x*ln(x)+5)/(sin(x^2+x^3-x^4)^2), x)\end{axiom}
```
Put the \begin{axiom} and \end{axiom} on separate lines and notice that in Axiom ln is written log
fricas
```
integrate((x^2+2*x*log(x)+5)/(sin(x^2+x^3-x^4)^2), x)
```
$\label{eq2}\int^{ \displaystyle x}{{\frac{-{2 \ \%G \ {\log \left({\%G}\right)}}-{{\%G}^{2}}- 5}{{{\cos \left({{{\%G}^{4}}-{{\%G}^{3}}-{{\%G}^{2}}}\right)}^{2}}- 1}}\ {d \%G}}$ (2)

Type: Union(Expression(Integer),...)
Don't put a \ in front of the axiom command
This is wrong:
```
    \begin{axiom}
    \sqrt{49/100}
    \end{axiom}
```
Begin each comment with an explanation. Don't put \ in front of the Axiom command.

Do it like this:
```
    Some explanation
    \begin{axiom}
    sqrt{49/100}
    \end{axiom}
```
Some explanation
fricas
```
sqrt{49/100}
```
$\label{eq3}\frac{7}{10}$ (3)

Type: AlgebraicNumber?
No $ before and after
This is wrong:
```
    \begin{axiom}
    $ \sqrt{49/100} $
    \end{axiom}
```
Don't put $ before and after $ and there is no \ in front.

Just do it like this:
```
    \begin{axiom}
    sqrt{49/100}
    \end{axiom}
```
and what you will see is this:
fricas
```
sqrt{49/100}
```
$\label{eq4}\frac{7}{10}$ (4)

Type: AlgebraicNumber?
Axiom sometimes interprets commands in unexpected ways
This command appears to work
fricas
```
integrate(x^5 ln[x],x)
```
$\label{eq5}\frac{{x}^{6}}{6}$ (5)

Type: Union(Expression(Integer),...)

But notice that
fricas
```
5 ln[x]
```
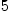
$\label{eq6}5$ (6)

Type: UnivariatePolynomial(ln[x],Integer)

is something strange. Oddly perhaps, Axiom interprets 5 as a UnivariatePolynomial and 'ln[x]' as a subscripted Symbol and the result is a univariate polynomial in the variable 'ln[x]'.

So perhaps what you meant to write was:
fricas
```
integrate(x^5*log(x),x)
```
$\label{eq7}\frac{{6 \ {{x}^{6}}\ {\log \left({x}\right)}}-{{x}^{6}}}{36}$ (7)

Type: Union(Expression(Integer),...)
Use braces not parenthesis after begin and end
The command:
```
    \begin(axiom)
    integrate(sin(x))
    \end(axiom)
```
wont work.

Use "braces" like this { } not parenthesis ( ) around {axiom}.

Finally, unless the expression is a univariate polynomial, then you must also specify the variable with which to integrate.
fricas
```
integrate(sin(x),x)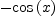
```
$\label{eq8}-{\cos \left({x}\right)}$ (8)

Type: Union(Expression(Integer),...)
Use parenthesis not braces in Axiom commands
This command:
```
    \begin{axiom}
    solve{xy=1,x}
    \end{axiom}
```
uses {} after the solve operation. This is syntactically correct but it probably doesn't do what you might expect.
fricas
```
solve{xy=1,x}
```
$\label{eq9}\left[{x = 0}\right]$ (9)

Type: List(Equation(Fraction(Polynomial(Integer))))

In Axiom {...,...} is executed as a block of commands which returns the result of the last command in the sequence. Compare
fricas
```
a:={xy=1,x}
```
$\label{eq10}x$ (10)

Type: Variable(x)

which is just x to
fricas
```
b:=(xy=1,x)
```
$\label{eq11}\left[{xy = 1}, \: x \right]$ (11)

Type: Tuple(Any)

solve normally operates on such a tuple and
fricas
```
c:=[xy=1,x]
```
$\label{eq12}\left[{xy = 1}, \: x \right]$ (12)

Type: List(Any)

which is a list and finally
fricas
```
c:=set [xy=1,x]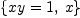
```
$\label{eq13}\left\{{xy = 1}, \: x \right\}$ (13)

Type: Set(Any)

which is how to construct a set.

Also notice that multiplication must be written using *
fricas
```
solve(x*y=1,x)
```
$\label{eq14}\left[{x ={\frac{1}{y}}}\right]$ (14)

Type: List(Equation(Fraction(Polynomial(Integer))))
Use %minusInfinity and %plusInfinity
I'd like to see if Axiom can do my favorite definite integral:
```
    \begin{axiom}
    integrate(x^4/(sinh(x))^2,x,-inf,inf)
    \end{axiom}
```
In Axiom use %minusInfinity and %plusInfinity instead of -inf and inf.
fricas
```
integrate(x^4/(sinh(x))^2,x=%minusInfinity..%plusInfinity)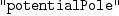
```
$\label{eq15}\verb#"potentialPole"#$ (15)

Type: Union(pole: potentialPole,...)
Numeric conversions
The results of calculations depend on the type of the inputs You can tell Axiom that you would like the result expressed as a floating point number (if possible) using @. For example:
fricas
```
asin(1/2)@Float
```
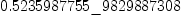
$\label{eq16}0.5235987755 \ 9829887308$ (16)

Type: Float
Axiom prefers symbolic calculations
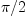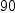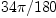The trig functions are expressed in radians so use $\pi/2$ instead and $34\pi/180$ instead of 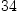. Finally, because Axiom prefers symbolic calculations express 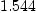as a rational number
fricas
```
r:Fraction Integer:=1.544
```
$\label{eq17}\frac{193}{125}$ (17)

Type: Fraction(Integer)

fricas
```
eq1:=90*%pi/180-asin(n*sin(34*%pi/180)/r)=asin(n/r)
```
$\label{eq18}\begin{array}{@{}l} \displaystyle {\frac{-{2 \ {\arcsin \left({\frac{{125}\ n \ {\sin \left({\frac{{1 7}\ \pi}{90}}\right)}}{193}}\right)}}+ \pi}{2}}= \ \ \displaystyle {\arcsin \left({\frac{{125}\ n}{193}}\right)}$ (18)

Type: Equation(Expression(Integer))

fricas
```
s:=solve(eq1,n)
```
$\label{eq19}\begin{array}{@{}l} \displaystyle \left[{ \begin{array}{@{}l} \displaystyle n = - \ \ \displaystyle {\frac{{386}\ {{e}^{\frac{{17}\ \pi \ {\sqrt{- 1}}}{90}}}}{{1 25}\ {\sqrt{-{{{e}^{\frac{{17}\ \pi \ {\sqrt{- 1}}}{90}}}^{4}}+{6 \ {{{e}^{\frac{{17}\ \pi \ {\sqrt{- 1}}}{90}}}^{2}}}- 1}}}}$ (19)

Type: List(Equation(Expression(Integer)))

Axiom thinks there are two solutions, unfortunately only one is valid:
fricas
```
eval(eq1,s.1)::Equation Expression Float
```
$\label{eq20}\begin{array}{@{}l} \displaystyle { \begin{array}{@{}l} \displaystyle {\arcsin \left({\frac{{1.1183858069 \ 414936603}\ {{e}^{{0.5 934119456 \ 7807205615}\ {\sqrt{-{1.0}}}}}}{\sqrt{-{{1.0}\ {{{e}^{{0.5934119456 \ 7807205615}\ {\sqrt{-{1.0}}}}}^{4}}}+{{6.0}\ {{{e}^{{0.5934119456 \ 7807205615}\ {\sqrt{-{1.0}}}}}^{2}}}-{1.0}}}}\right)}+ \ \ \displaystyle {1.5707963267 \ 948966192}$ (20)

Type: Equation(Expression(Float))

fricas
```
eval(eq1,s.2)::Equation Expression Float
```
$\label{eq21}\begin{array}{@{}l} \displaystyle { \begin{array}{@{}l} \displaystyle -{{1.0}\ {\arcsin \left({\frac{{1.1183858069 \ 414936603}\ {{e}^{{0.5934119456 \ 7807205615}\ {\sqrt{-{1.0}}}}}}{\sqrt{-{{1.0}\ {{{e}^{{0.5934119456 \ 7807205615}\ {\sqrt{-{1.0}}}}}^{4}}}+{{6.0}\ {{{e}^{{0.5934119456 \ 7807205615}\ {\sqrt{-{1.0}}}}}^{2}}}-{1.0}}}}\right)}}+{1.5707963267 \ 948966192}$ (21)

Type: Equation(Expression(Float))

Coercion is sometimes necessary

For example

fricas

integrate((4 - x**2)**.5::Expression Fraction Integer, x)

   There are no library operations named ** 
      Use HyperDoc Browse or issue
                                 )what op **
      to learn if there is any operation containing " ** " in its name.

   Cannot find a definition or applicable library operation named ** 
      with argument type(s) 
                                 Variable(x)
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Use either differentiate or the abbreviation D
Since sin(x) cannot be interpreted as a univariate polynomial, you must specify the integration variable.
fricas
```
differentiate(sin(x),x)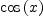
```
$\label{eq22}\cos \left({x}\right)$ (22)

Type: Expression(Integer)
MathAction requires that Axiom library code must beging with )abbrev. Typing )abb is not enough even though that works in Axiom itself.