A complex vector CC-space  possesses many different hermitian isomorphisms
possesses many different hermitian isomorphisms
 . In quantum mechanics a given operator
. In quantum mechanics a given operator
 may be said to be
may be said to be 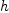 -hermitian if
-hermitian if
fricas
)set output tex off
fricas
)set output algebra on
fricas
CC:=Complex Fraction Polynomial Integer
(1) Complex(Fraction(Polynomial(Integer)))
Type: Type
fricas
-- dagger
htranspose(h)==map(x+->conjugate(x),transpose h)
Type: Void
fricas
)expose MCALCFN
MultiVariableCalculusFunctions is now explicitly exposed in frame
initial
Theorem
The necessary conditions for an operator  to possess hermitean isomorphism
to possess hermitean isomorphism
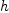 is that
is that  and
and  .
.
Two-Dimensions
fricas
p1:CC:=complex(Rp1,Ip1)
(3) Rp1 + Ip1 %i
Type: Complex(Fraction(Polynomial(Integer)))
fricas
q1:CC:=complex(Rq1,Iq1)
(4) Rq1 + Iq1 %i
Type: Complex(Fraction(Polynomial(Integer)))
fricas
p2:CC:=complex(Rp2,Ip2)
(5) Rp2 + Ip2 %i
Type: Complex(Fraction(Polynomial(Integer)))
fricas
q2:CC:=complex(Rq2,Iq2)
(6) Rq2 + Iq2 %i
Type: Complex(Fraction(Polynomial(Integer)))
fricas
rho:Matrix CC := matrix [[p1,q1],[p2,q2]]
+Rp1 + Ip1 %i Rq1 + Iq1 %i+
(7) | |
+Rp2 + Ip2 %i Rq2 + Iq2 %i+
Type: Matrix(Complex(Fraction(Polynomial(Integer))))
fricas
s1:=solve(imag determinant rho,Rp2)
Ip1 Rq2 - Ip2 Rq1 + Iq2 Rp1
(8) [Rp2 = ---------------------------]
Iq1
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
s2:=solve(eval(imag trace rho,s1),Ip1)
(9) [Ip1 = - Iq2]
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
s3:=solve(eval(eval(imag trace(rho*rho),s1), s2),Rp1)
(10) [0 = 0]
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
eval(eval(imag trace (rho*rho),s1),s2)
(11) 0
Type: Fraction(Polynomial(Integer))
fricas
C:=eval(eval(characteristicPolynomial rho,s1),s2)
(12)
2
(Iq2 Rq1 + Iq1 Rp1 - %B Iq1)Rq2 + Ip2 Rq1 - Iq2 Rp1 Rq1 - %B Iq1 Rp1
+
2 2 2
Iq1 Iq2 + Ip2 Iq1 + %B Iq1
/
Iq1
Type: Fraction(Polynomial(Complex(Integer)))
fricas
C0:=zerosOf(C)
(13)
[
ROOT
2 2
Iq1 Rq2 + (- 4 Iq2 Rq1 - 2 Iq1 Rp1)Rq2 - 4 Ip2 Rq1
+
2 2 2
4 Iq2 Rp1 Rq1 + Iq1 Rp1 - 4 Iq1 Iq2 - 4 Ip2 Iq1
/
Iq1
+
Rq2 + Rp1
/
2
,
-
ROOT
2 2
Iq1 Rq2 + (- 4 Iq2 Rq1 - 2 Iq1 Rp1)Rq2 - 4 Ip2 Rq1
+
2 2 2
4 Iq2 Rp1 Rq1 + Iq1 Rp1 - 4 Iq1 Iq2 - 4 Ip2 Iq1
/
Iq1
+
Rq2 + Rp1
/
2
]
Type: List(Expression(Complex(Integer)))
fricas
#C0
(14) 2
fricas
imag(C0.1)
(15) 0
Type: Expression(Integer)
fricas
imag(C0.2)
(16) 0
Type: Expression(Integer)
fricas
rho0:=map(x+->eval(eval(x,s1),s2),rho)
+ Rp1 - %i Iq2 Rq1 + %i Iq1+
| |
(17) |- Iq2 Rq2 - Ip2 Rq1 + Iq2 Rp1 + %i Ip2 Iq1 |
|------------------------------------------ Rq2 + %i Iq2|
+ Iq1 +
Type: Matrix(Fraction(Polynomial(Complex(Integer))))
fricas
E:=eigenvalues(rho0)
(18)
[
%D
|
2
(Iq2 Rq1 + Iq1 Rp1 - %D Iq1)Rq2 + Ip2 Rq1 - Iq2 Rp1 Rq1 - %D Iq1 Rp1
+
2 2 2
Iq1 Iq2 + Ip2 Iq1 + %D Iq1
]
Type: List(Union(Fraction(Polynomial(Complex(Integer))),
SuchThat
?(Symbol,
Polynomial(Complex(Integer)))))
fricas
E0:=eigenvector(E.1,rho0)
+ Iq1 Rq2 + %i Iq1 Iq2 - %D Iq1 +
|----------------------------------------|
(19) [|Iq2 Rq2 + Ip2 Rq1 - Iq2 Rp1 - %i Ip2 Iq1|]
| |
+ 1 +
Type: List(Matrix(Fraction(Polynomial(Complex(Integer)))))
fricas
E1:=map(x+->eval(x,%D=C0.1),E0.1)
(20)
[
[
-
Iq1
*
ROOT
2 2
Iq1 Rq2 + (- 4 Iq2 Rq1 - 2 Iq1 Rp1)Rq2 - 4 Ip2 Rq1
+
2 2 2
4 Iq2 Rp1 Rq1 + Iq1 Rp1 - 4 Iq1 Iq2 - 4 Ip2 Iq1
/
Iq1
+
Iq1 Rq2 - Iq1 Rp1 + 2 %i Iq1 Iq2
/
2 Iq2 Rq2 + 2 Ip2 Rq1 - 2 Iq2 Rp1 - 2 %i Ip2 Iq1
]
,
[1]]
Type: Matrix(Expression(Complex(Integer)))
fricas
E2:=map(x+->eval(x,%D=C0.2),E0.1)
(21)
[
[
Iq1
*
ROOT
2 2
Iq1 Rq2 + (- 4 Iq2 Rq1 - 2 Iq1 Rp1)Rq2 - 4 Ip2 Rq1
+
2 2 2
4 Iq2 Rp1 Rq1 + Iq1 Rp1 - 4 Iq1 Iq2 - 4 Ip2 Iq1
/
Iq1
+
Iq1 Rq2 - Iq1 Rp1 + 2 %i Iq1 Iq2
/
2 Iq2 Rq2 + 2 Ip2 Rq1 - 2 Iq2 Rp1 - 2 %i Ip2 Iq1
]
,
[1]]
Type: Matrix(Expression(Complex(Integer)))
fricas
test(rho0*E1=C0(1)*E1)
(22) true
Type: Boolean
fricas
test(rho0*E2=C0(2)*E2)
(23) true
Type: Boolean
Given an operator  , one must find the tensor
, one must find the tensor 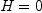 for unknown manifold of hermitian isomorphisms
for unknown manifold of hermitian isomorphisms 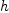 .
.
fricas
h:Matrix CC:=matrix [[Ra,complex(Rb,Ib)],[complex(Rb,-Ib),Re]]
+ Ra Rb + Ib %i+
(24) | |
+Rb - Ib %i Re +
Type: Matrix(Complex(Fraction(Polynomial(Integer))))
fricas
test(h = htranspose h)
fricas
Compiling function htranspose with type Matrix(Complex(Fraction(
Polynomial(Integer)))) -> Matrix(Complex(Fraction(Polynomial(
Integer))))
(25) trueType: Boolean
fricas
H:=htranspose(rho)*h-h*rho
(26)
[
[(- 2 Ib Rp2 - 2 Ip2 Rb - 2 Ip1 Ra)%i,
- Rb Rq2 - Ra Rq1 + Re Rp2 + Rb Rp1 + Ib Iq2 + Ib Ip1
+
(- Ib Rq2 + Ib Rp1 - Ip2 Re + (- Iq2 - Ip1)Rb - Iq1 Ra)%i
]
,
[
Rb Rq2 + Ra Rq1 - Re Rp2 - Rb Rp1 - Ib Iq2 - Ib Ip1
+
(- Ib Rq2 + Ib Rp1 - Ip2 Re + (- Iq2 - Ip1)Rb - Iq1 Ra)%i
,
(2 Ib Rq1 - 2 Iq2 Re - 2 Iq1 Rb)%i]
]
Type: Matrix(Complex(Fraction(Polynomial(Integer))))
We wish to find expressions for 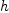 in terms of the components of
in terms of the components of
 . To do this we will determine how the components of
. To do this we will determine how the components of 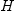 depend
on the components of
depend
on the components of 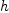 .
.
fricas
J:=jacobian(concat( map(x+->[real x, imag x], concat(H::List List ?)) ),
[Ra,Rb,Ib,Re]::List Symbol)
+ 0 0 0 0 +
| |
|- 2 Ip1 - 2 Ip2 - 2 Rp2 0 |
| |
| - Rq1 - Rq2 + Rp1 Iq2 + Ip1 Rp2 |
| |
| - Iq1 - Iq2 - Ip1 - Rq2 + Rp1 - Ip2 |
(27) | |
| Rq1 Rq2 - Rp1 - Iq2 - Ip1 - Rp2 |
| |
| - Iq1 - Iq2 - Ip1 - Rq2 + Rp1 - Ip2 |
| |
| 0 0 0 0 |
| |
+ 0 - 2 Iq1 2 Rq1 - 2 Iq2+
Type: Matrix(Fraction(Polynomial(Integer)))
The null space (kernel) of the Jacobian
fricas
N:=nullSpace(map(x+->eval(eval(x,s1),s2),J))
- Rq2 + Rp1 Rq1 Ip2 Iq2
(28) [[-----------, ---, 1, 0], [- ---, - ---, 0, 1]]
Iq1 Iq1 Iq1 Iq1
Type: List(Vector(Fraction(Polynomial(Integer))))
gives the general solution to the problem.
fricas
s4:=map((x,y)+->x=y,[Ra,Rb,Rb,Re],Ib*N.1+Re*N.2)
(29)
- Ib Rq2 + Ib Rp1 - Ip2 Re Ib Rq1 - Iq2 Re
[Ra = --------------------------, Rb = ---------------, Rb = Ib, Re = Re]
Iq1 Iq1
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
map(x+->eval(eval(eval(x,s1),s2),s4),H)
+0 0+
(30) | |
+0 0+
Type: Matrix(Fraction(Polynomial(Complex(Integer))))
Three-Dimensions
fricas
p1:CC:=complex(Rp1,Ip1)
(31) Rp1 + Ip1 %i
Type: Complex(Fraction(Polynomial(Integer)))
fricas
q1:CC:=complex(Rq1,Iq1)
(32) Rq1 + Iq1 %i
Type: Complex(Fraction(Polynomial(Integer)))
fricas
r1:CC:=complex(Rr1,Ir1)
(33) Rr1 + Ir1 %i
Type: Complex(Fraction(Polynomial(Integer)))
fricas
p2:CC:=complex(Rp2,Ip2)
(34) Rp2 + Ip2 %i
Type: Complex(Fraction(Polynomial(Integer)))
fricas
q2:CC:=complex(Rq2,Iq2)
(35) Rq2 + Iq2 %i
Type: Complex(Fraction(Polynomial(Integer)))
fricas
r2:CC:=complex(Rr2,Ir2)
(36) Rr2 + Ir2 %i
Type: Complex(Fraction(Polynomial(Integer)))
fricas
p3:CC:=complex(Rp3,Ip3)
(37) Rp3 + Ip3 %i
Type: Complex(Fraction(Polynomial(Integer)))
fricas
q3:CC:=complex(Rq3,Iq3)
(38) Rq3 + Iq3 %i
Type: Complex(Fraction(Polynomial(Integer)))
fricas
r3:CC:=complex(Rr3,Ir3)
(39) Rr3 + Ir3 %i
Type: Complex(Fraction(Polynomial(Integer)))
fricas
rho:Matrix CC := matrix [[p1,q1,r1],[p2,q2,r2],[p3,q3,r3]]
+Rp1 + Ip1 %i Rq1 + Iq1 %i Rr1 + Ir1 %i+
| |
(40) |Rp2 + Ip2 %i Rq2 + Iq2 %i Rr2 + Ir2 %i|
| |
+Rp3 + Ip3 %i Rq3 + Iq3 %i Rr3 + Ir3 %i+
Type: Matrix(Complex(Fraction(Polynomial(Integer))))
fricas
s1:=solve(imag determinant rho,Rp3)
(41)
[
Rp3
=
(- Ip1 Rq2 + Ip2 Rq1 + Iq1 Rp2 - Iq2 Rp1)Rr3
+
(Ip1 Rq3 - Ip3 Rq1 + Iq3 Rp1)Rr2 + (- Ip2 Rq3 + Ip3 Rq2 - Iq3 Rp2)Rr1
+
(- Ir1 Rp2 + Ir2 Rp1)Rq3 - Ir3 Rp1 Rq2 + Ir3 Rp2 Rq1
+
(Ip1 Iq2 - Ip2 Iq1)Ir3 + (- Ip1 Iq3 + Ip3 Iq1)Ir2
+
(Ip2 Iq3 - Ip3 Iq2)Ir1
/
Iq1 Rr2 - Iq2 Rr1 - Ir1 Rq2 + Ir2 Rq1
]
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
s2:=solve(eval(imag trace(rho),s1),Ip1)
(42) [Ip1 = - Ir3 - Iq2]
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
s3:=solve(eval(eval(imag trace(rho*rho),s1),s2),Rp1)
(43)
[
Rp1
=
Iq1 Ir3 Rr2 - Iq2 Ir3 Rr1 + Iq2 Ir1 Rq2 + (Ir2 Ir3 + Ip2 Ir1)Rq1
+
Iq1 Ir1 Rp2
*
Rr3
+
2
Iq1 Iq3 Rr2
+
(- Iq2 Iq3 + Ip3 Iq1)Rr1 + (- Ir1 Ir3 + Iq1 Ir2 - Iq2 Ir1)Rq3
+
(- Iq3 Ir1 + Iq1 Iq2)Rq2 + (Iq3 Ir2 - Ip3 Ir1 + Ip2 Iq1)Rq1
+
2
Iq1 Rp2
*
Rr2
+
2
- Ip3 Iq2 Rr1
+
2
(- Iq2 Ir2 - Ip2 Ir1)Rq3 - Iq2 Rq2 + (Ip3 Ir2 - Ip2 Iq2)Rq1
+
(- Iq3 Ir1 - Iq1 Iq2)Rp2
*
Rr1
+
2 2 2
(- Ir1 Ir2 Rq2 + Ir2 Rq1 - Ir1 Rp2)Rq3 - Iq2 Ir1 Rq2
+
2
((Iq2 Ir2 - Ip2 Ir1)Rq1 - Iq1 Ir1 Rp2)Rq2 + Ip2 Ir2 Rq1
+
2
(Ir1 Ir3 + Iq1 Ir2)Rp2 Rq1 - Iq2 Ir1 Ir3
+
2
(Iq3 Ir1 Ir2 + (- Iq2 - Ip2 Iq1)Ir1)Ir3 + (Iq2 Iq3 + Ip3 Iq1)Ir1 Ir2
+
2
(Ip2 Iq3 - Ip3 Iq2)Ir1
/
Iq2 Ir1 Rr3 + (Iq1 Ir3 - Iq3 Ir1 + Iq1 Iq2)Rr2
+
2
(- Iq2 Ir3 - Iq2 )Rr1 - Ir1 Ir2 Rq3 - Iq2 Ir1 Rq2
+
(Ir2 Ir3 + Iq2 Ir2)Rq1
]
Type: List(Equation(Fraction(Polynomial(Integer))))
fricas
eval(eval(eval(imag trace(rho*rho*rho),s1),s2),s3)
(44) 0
Type: Fraction(Polynomial(Integer))
fricas
C:=eval(eval(eval(characteristicPolynomial rho,s1),s2),s3)
(45)
2
(Iq1 Ir3 Rq2 - Iq2 Ir3 Rq1 - %E Iq1 Ir3)Rr2 + Iq2 Ir1 Rq2
+
((Ir2 Ir3 + Ip2 Ir1)Rq1 + Iq1 Ir1 Rp2 - 2 %E Iq2 Ir1)Rq2
+
(- Iq2 Ir1 Rp2 - %E Ir2 Ir3 - %E Ip2 Ir1)Rq1 - %E Iq1 Ir1 Rp2
+
3 2
Iq1 Iq2 Ir2 Ir3 + (Iq2 + (Ip2 Iq1 + %E )Iq2)Ir1
*
2
Rr3
+
(- Iq1 Ir3 Rq3 + Iq1 Iq3 Rq2 + (Iq3 Ir3 - Iq2 Iq3)Rq1 - %E Iq1 Iq3)
*
2
Rr2
+
Iq2 Ir3 Rq3 + (- Iq3 Ir3 + Ip3 Iq1)Rq2 - Ip3 Iq2 Rq1
+
%E Iq3 Ir3 - %E Ip3 Iq1
*
Rr1
+
(- Ir1 Ir3 + Iq1 Ir2 - 2 Iq2 Ir1)Rq2
+
(- Iq2 Ir2 - Ip2 Ir1)Rq1 - Iq1 Ir1 Rp2 + %E Ir1 Ir3
+
- %E Iq1 Ir2 + 2 %E Iq2 Ir1
*
Rq3
+
2
(- Iq3 Ir1 + Iq1 Iq2)Rq2
+
2
(2 Iq2 Ir3 + Iq3 Ir2 - Ip3 Ir1 + Ip2 Iq1)Rq1 + Iq1 Rp2
+
- 2 %E Iq1 Ir3 + 2 %E Iq3 Ir1 - 2 %E Iq1 Iq2
*
Rq2
+
2
Ip2 Ir3 Rq1
+
((Iq3 Ir1 - Iq1 Iq2)Rp2 - %E Iq3 Ir2 + %E Ip3 Ir1 - %E Ip2 Iq1)
*
Rq1
+
2
- %E Iq1 Rp2
+
2 2 2
(- Iq2 Iq3 Ir1 + 2 Iq1 Iq2 + Ip2 Iq1 + 2 %E Iq1)Ir3
+
Iq1 Iq2 Iq3 Ir2
+
2 2 3
((- 3 Iq2 - Ip2 Iq1 - %E )Iq3 - Ip3 Iq1 Iq2)Ir1 + Iq1 Iq2
+
2 2
(Ip2 Iq1 + %E Iq1)Iq2
*
Rr2
+
(- Ir2 Ir3 - Ip2 Ir1)Rq2 + Iq2 Ir1 Rp2 + %E Ir2 Ir3
+
%E Ip2 Ir1
*
Rq3
+
2 2
(- 2 Iq2 Ir3 - Iq2 )Rq2
+
(- Ip2 Ir3 + Ip3 Ir2 - Ip2 Iq2)Rq1
+
2
(- Iq1 Ir3 - Iq3 Ir1 - Iq1 Iq2)Rp2 + 4 %E Iq2 Ir3 + 2 %E Iq2
*
Rq2
+
2
((Iq2 Ir3 + Iq2 )Rp2 + %E Ip2 Ir3 - %E Ip3 Ir2 + %E Ip2 Iq2)Rq1
+
(%E Iq1 Ir3 + %E Iq3 Ir1 + %E Iq1 Iq2)Rp2
+
3 2
(- Iq2 Iq3 Ir2 - 2 Iq2 + (- Ip2 Iq1 - 2 %E )Iq2)Ir3
+
4 2 2
Ip3 Iq1 Iq2 Ir2 - Ip2 Iq2 Iq3 Ir1 - Iq2 + (- Ip2 Iq1 - %E )Iq2
*
Rr1
+
2 2 2
- Ir1 Ir2 Rq2 + (Ir2 Rq1 - Ir1 Rp2 + 2 %E Ir1 Ir2)Rq2
+
2 2
(Ir1 Ir2 Rp2 - %E Ir2 )Rq1 + %E Ir1 Rp2
+
2 2
(- Iq1 Ir2 - Iq2 Ir1 Ir2)Ir3 + Iq1 Iq2 Ir2
+
2 2 2
(- 3 Iq2 - Ip2 Iq1 - %E )Ir1 Ir2 - Ip2 Iq2 Ir1
*
Rq3
+
3
- Iq2 Ir1 Rq2
+
2
((Iq2 Ir2 - Ip2 Ir1)Rq1 - Iq1 Ir1 Rp2 + %E Iq2 Ir1)Rq2
+
2
Ip2 Ir2 Rq1
+
(Ir1 Ir3 + Iq1 Ir2 + Iq2 Ir1)Rp2 - 2 %E Ir2 Ir3
+
- 2 %E Iq2 Ir2
*
Rq1
+
((Iq3 Ir1 - 2 Iq1 Iq2)Ir2 - Ip2 Iq1 Ir1)Ir3
+
2
(2 Iq2 Iq3 + Ip3 Iq1)Ir1 Ir2 + Ip2 Iq3 Ir1
+
3 2
(- Iq2 + (- Ip2 Iq1 + %E )Iq2)Ir1
*
Rq2
+
2
((- Ir2 Ir3 - Iq2 Ir2)Rp2 - %E Ip2 Ir2)Rq1
+
(- %E Ir1 Ir3 - %E Iq1 Ir2 + %E Iq2 Ir1)Rp2
+
2 2 2
(Iq3 Ir2 + (2 Iq2 + 2 %E )Ir2 + Ip2 Iq2 Ir1)Ir3
+
3 2
((Ip2 Iq3 - Ip3 Iq2)Ir1 + Iq2 + (Ip2 Iq1 + %E )Iq2)Ir2
+
2
%E Ip2 Ir1
*
Rq1
+
2 2
(- Iq1 Ir2 + Iq1 Iq2 Ir1)Ir3 + Iq1 Iq3 Ir1 Ir2 - Iq2 Iq3 Ir1
+
2
%E Iq1 Ir1
*
Rp2
+
(- %E Iq3 Ir1 Ir2 + %E Ip2 Iq1 Ir1)Ir3
+
2
(- 2 %E Iq2 Iq3 - %E Ip3 Iq1)Ir1 Ir2 - %E Ip2 Iq3 Ir1
+
3 3
(- %E Iq2 + (- %E Ip2 Iq1 - %E )Iq2)Ir1
*
Rr3
+
2 3
(- Iq1 Iq3 Rq3 + Iq3 Rq1)Rr2
+
2 2
((Iq2 Iq3 - Ip3 Iq1)Rq3 - Iq3 Rq2 + Ip3 Iq3 Rq1 + %E Iq3 )Rr1
+
2
(Ir1 Ir3 - Iq1 Ir2 + Iq2 Ir1)Rq3
+
(Iq3 Ir1 - Iq1 Iq2)Rq2
+
2 2
(- Ir3 - 2 Iq2 Ir3 + Iq3 Ir2 + Ip3 Ir1 - Iq2 - Ip2 Iq1)Rq1
+
2
- Iq1 Rp2 + %E Iq1 Ir3 - %E Iq3 Ir1 + %E Iq1 Iq2
*
Rq3
+
((- Iq3 Ir3 + Iq2 Iq3)Rq1 - %E Iq1 Iq3)Rq2
+
2 2
(- Ip3 Ir3 + Ip2 Iq3 - Ip3 Iq2)Rq1 + Iq1 Iq3 Rp2 Rq1 - Iq1 Iq3 Ir3
+
2 2
(Iq3 Ir1 - 3 Iq1 Iq2 Iq3 - Ip3 Iq1 )Ir3
+
2 2 2 2
(2 Iq2 Iq3 + Ip3 Iq1 Iq3)Ir1 + (- Iq1 Iq2 + %E Iq1)Iq3 - Ip3 Iq1 Iq2
*
2
Rr2
+
2
(Ip3 Iq2 Rq3 - Ip3 Iq3 Rq2 + %E Ip3 Iq3)Rr1
+
2
(Iq2 Ir2 + Ip2 Ir1)Rq3
+
2 2
(Ir3 + 2 Iq2 Ir3 - 2 Iq3 Ir2 + 2 Iq2 )Rq2 - Ip2 Ir3 Rq1
+
2
(Iq1 Ir3 + 2 Iq1 Iq2)Rp2 - %E Ir3 - 3 %E Iq2 Ir3
+
2
2 %E Iq3 Ir2 - 2 %E Iq2
*
Rq3
+
2
(Iq3 Ir3 - Iq2 Iq3)Rq2
+
(Ip3 Ir3 - Ip2 Iq3 + 2 Ip3 Iq2)Rq1 - Iq1 Iq3 Rp2 - %E Iq3 Ir3
+
2 %E Iq2 Iq3 - %E Ip3 Iq1
*
Rq2
+
(- Iq3 Ir3 - Iq2 Iq3)Rp2 - %E Ip3 Ir3 + %E Ip2 Iq3
+
- %E Ip3 Iq2
*
Rq1
+
2
%E Iq1 Iq3 Rp2 + Iq2 Iq3 Ir3
+
2 2
((3 Iq2 - Ip2 Iq1)Iq3 + Ip3 Iq1 Iq2)Ir3 - Iq2 Iq3 Ir2
+
2 3 2 2
Ip2 Iq3 Ir1 + (Iq2 + (- Ip2 Iq1 - %E )Iq2)Iq3 + 2 Ip3 Iq1 Iq2
+
2
%E Ip3 Iq1
*
Rr1
+
2 2
(Ir1 Ir2 Rq2 + Ir1 Rp2 - %E Ir1 Ir2)Rq3
+
2
Iq2 Ir1 Rq2
+
(- Ir2 Ir3 + Ip2 Ir1)Rq1 + Iq1 Ir1 Rp2 + %E Ir1 Ir3
+
- %E Iq1 Ir2
*
Rq2
+
((- 2 Ir1 Ir3 - Iq2 Ir1)Rp2 + %E Ir2 Ir3 + %E Iq2 Ir2)Rq1
+
2 2 2
Iq2 Ir1 Ir3 + (- Iq1 Iq2 Ir2 - %E Ir1)Ir3 - Iq1 Iq3 Ir2
+
2 2
(2 Iq2 Iq3 Ir1 + %E Iq1)Ir2 + Ip3 Iq2 Ir1
+
3 2
(- Iq2 + (- Ip2 Iq1 - %E )Iq2)Ir1
*
Rq3
+
2
(- Iq2 Ir3 Rq1 + %E Iq3 Ir1 - %E Iq1 Iq2)Rq2
+
2
- Ip2 Ir3 Rq1
+
(- Iq1 Ir3 Rp2 - %E Iq3 Ir2 + %E Ip3 Ir1 - %E Ip2 Iq1)Rq1
+
2 3 2
- %E Iq1 Rp2 + Iq1 Ir3 + (- Iq3 Ir1 + 2 Iq1 Iq2)Ir3
+
2 2
(Iq1 Iq3 Ir2 + Ip3 Iq1 Ir1 + %E Iq1)Ir3 - Iq3 Ir1 Ir2
+
2 2 2
- Ip3 Iq3 Ir1 + ((2 Iq2 - 2 %E )Iq3 + 2 Ip3 Iq1 Iq2)Ir1
+
2
2 %E Iq1 Iq2
*
Rq2
+
2 2
(Ir3 + Iq2 Ir3)Rp2 Rq1
+
3 2 2
(%E Iq1 Ir3 - %E Iq3 Ir1 + %E Iq1 Iq2)Rp2 - Iq2 Ir3 - 2 Iq2 Ir3
+
3 2 2
(- Iq2 Iq3 Ir2 - Ip3 Iq2 Ir1 - Iq2 - Ip2 Iq1 Iq2)Ir3 + Iq3 Ir2
+
2 2 2 2
%E Iq3 Ir2 + (2 Ip2 Iq2 Iq3 - 2 Ip3 Iq2 - %E Ip3)Ir1 + %E Ip2 Iq1
*
Rq1
+
2 2 2 2 2 2 3
(Iq1 Ir3 - 2 Iq1 Iq3 Ir1 Ir3 + Iq3 Ir1 + %E Iq1 )Rp2 - %E Iq1 Ir3
+
2
(%E Iq3 Ir1 - 2 %E Iq1 Iq2)Ir3
+
2
- %E Iq1 Iq3 Ir2 + (%E Iq2 Iq3 - %E Ip3 Iq1)Ir1 - 2 %E Iq1 Iq2
+
2 3
- %E Ip2 Iq1 - %E Iq1
*
Ir3
+
2 2
(%E Iq3 Ir1 - %E Iq1 Iq2 Iq3)Ir2 + %E Ip3 Iq3 Ir1
+
2 3 3
((%E Iq2 + %E Ip2 Iq1 + %E )Iq3 - %E Ip3 Iq1 Iq2)Ir1 - %E Iq1 Iq2
+
2 3
(- %E Ip2 Iq1 - %E Iq1)Iq2
*
Rr2
+
2
(Ip2 Ir3 - Ip3 Ir2 + Ip2 Iq2)Rq2 + (- Iq2 Ir3 - Iq2 )Rp2
+
- %E Ip2 Ir3 + %E Ip3 Ir2 - %E Ip2 Iq2
*
Rq3
+
2
- Ip3 Iq2 Rq2 + ((Iq3 Ir3 + Iq2 Iq3)Rp2 + 2 %E Ip3 Iq2)Rq2
+
(- %E Iq3 Ir3 - %E Iq2 Iq3)Rp2 + Ip2 Iq2 Iq3 Ir3 - Ip3 Iq2 Iq3 Ir2
+
2 3 2
Ip2 Iq2 Iq3 - Ip3 Iq2 - %E Ip3 Iq2
*
2
Rr1
+
2 2 2
(- Ir2 Rq2 - Ir1 Ir2 Rp2 + %E Ir2 )Rq3
+
2
(Ir2 Ir3 - Iq2 Ir2)Rq2
+
- Ip2 Ir2 Rq1 + (Ir1 Ir3 - Iq1 Ir2)Rp2 - %E Ir2 Ir3
+
2 %E Iq2 Ir2 + %E Ip2 Ir1
*
Rq2
+
((Ir2 Ir3 + Iq2 Ir2)Rp2 + %E Ip2 Ir2)Rq1
+
2
(- %E Ir1 Ir3 + %E Iq1 Ir2 - %E Iq2 Ir1)Rp2 + Iq2 Ir2 Ir3
+
2
((3 Iq2 + Ip2 Iq1)Ir2 + Ip2 Iq2 Ir1)Ir3
+
2 3 2
(- Iq2 Iq3 - Ip3 Iq1)Ir2 + (Iq2 + (Ip2 Iq1 - %E )Iq2)Ir2
+
2
- %E Ip2 Ir1
*
Rq3
+
3 2 2
Iq2 Ir3 Rq2 + (Ip2 Ir3 Rq1 + Iq1 Ir3 Rp2 - %E Iq2 Ir3 + %E Iq2 )Rq2
+
2
((- Ir3 - Iq2 Ir3)Rp2 - %E Ip2 Ir3 - %E Ip3 Ir2 + %E Ip2 Iq2)Rq1
+
(- %E Iq1 Ir3 + %E Iq3 Ir1 + %E Iq1 Iq2)Rp2
+
2
(- Iq3 Ir2 + Ip2 Iq1)Ir3
+
3
(- 2 Iq2 Iq3 - Ip3 Iq1)Ir2 - Ip2 Iq3 Ir1 + Iq2
+
2
(Ip2 Iq1 - %E )Iq2
*
Ir3
+
2 2 2
(- 2 Iq2 Iq3 - 2 Ip3 Iq1 Iq2)Ir2 - 2 %E Iq2
*
Rq2
+
2 2 2
(%E Ir3 - %E Iq2 )Rp2 - Ip2 Iq2 Ir3
+
2
(- Ip2 Iq3 + Ip3 Iq2)Ir2 Ir3 + Ip3 Iq3 Ir2
+
2 2 2
(- 2 Ip2 Iq2 Iq3 + 2 Ip3 Iq2 + %E Ip3)Ir2 - %E Ip2 Iq2
*
Rq1
+
2 2
- Iq1 Iq2 Ir3 + (Iq1 Iq3 Ir2 + Iq2 Iq3 Ir1)Ir3 - Iq3 Ir1 Ir2
+
2 2
- %E Iq3 Ir1 - %E Iq1 Iq2
*
Rp2
+
2
(%E Iq3 Ir2 - %E Ip2 Iq1)Ir3
+
3
(3 %E Iq2 Iq3 + %E Ip3 Iq1)Ir2 + %E Ip2 Iq3 Ir1 + %E Iq2
+
3
%E Iq2
*
Ir3
+
2 4
(2 %E Iq2 Iq3 + %E Ip3 Iq1 Iq2)Ir2 + %E Ip2 Iq2 Iq3 Ir1 + %E Iq2
+
3 2
(%E Ip2 Iq1 + %E )Iq2
*
Rr1
+
2 3 2 2 2
(Ir1 Ir2 Ir3 - Iq1 Ir2 + 2 Iq2 Ir1 Ir2 + Ip2 Ir1 Ir2)Rq3
+
2
%E Ir1 Ir2 Rq2
+
2 2 2 2
- %E Ir2 Rq1 + %E Ir1 Rp2 - Ir1 Ir2 Ir3 + Iq1 Ir2 Ir3
+
2 2 2 2
(- Iq3 Ir1 - Iq1 Iq2)Ir2 + (- Ip3 Ir1 + (2 Iq2 - 2 %E )Ir1)Ir2
+
2
Ip2 Iq2 Ir1
*
Rq2
+
2 2 2
- %E Ir1 Ir2 Rp2 - Ir2 Ir3 + (- 3 Iq2 Ir2 - 2 Ip2 Ir1 Ir2)Ir3
+
3 2 2 2
Iq3 Ir2 + (Ip3 Ir1 - Iq2 - Ip2 Iq1 + %E )Ir2
*
Rq1
+
2 2 2 2 2
(- Iq1 Ir2 + 2 Iq1 Iq2 Ir1 Ir2 + (- Iq2 - %E )Ir1 )Rp2
+
2 2
%E Ir1 Ir2 Ir3 + %E Iq2 Ir1 Ir2 Ir3 + %E Iq3 Ir1 Ir2
+
2 2 3
(%E Ip3 Ir1 + (%E Iq2 + %E Ip2 Iq1 + %E )Ir1)Ir2
*
Rq3
+
3
%E Iq2 Ir1 Rq2
+
2
(- %E Iq2 Ir2 + %E Ip2 Ir1)Rq1 + %E Iq1 Ir1 Rp2 - Iq2 Ir1 Ir3
+
2 2
(Iq1 Iq2 Ir2 - Iq2 Ir1)Ir3 - Iq2 Iq3 Ir1 Ir2 - Ip3 Iq2 Ir1
+
2
- 2 %E Iq2 Ir1
*
2
Rq2
+
2
- %E Ip2 Ir2 Rq1
+
3
(- %E Ir1 Ir3 - %E Iq1 Ir2 - %E Iq2 Ir1)Rp2 + Ir2 Ir3
+
2 2
2 Iq2 Ir2 Ir3 + ((Ip3 Ir1 + Ip2 Iq1 + %E )Ir2 - Ip2 Iq2 Ir1)Ir3
+
2 2
Iq2 Iq3 Ir2 + ((- Ip2 Iq3 + 2 Ip3 Iq2)Ir1 + 2 %E Iq2)Ir2
+
2
- %E Ip2 Ir1
*
Rq1
+
2 2
(Iq1 Ir2 - Iq1 Iq2 Ir1)Ir3 - Iq1 Iq3 Ir1 Ir2 + Iq2 Iq3 Ir1
+
2
- %E Iq1 Ir1
*
Rp2
+
2
2 %E Iq2 Ir1 Ir3
+
2
(- %E Iq3 Ir1 Ir2 + (2 %E Iq2 + %E Ip2 Iq1)Ir1)Ir3
+
2
- %E Ip3 Iq1 Ir1 Ir2 + (- %E Ip2 Iq3 + 2 %E Ip3 Iq2)Ir1
+
3 3
(%E Iq2 + (%E Ip2 Iq1 + %E )Iq2)Ir1
*
Rq2
+
2 2
(%E Ir2 Ir3 + %E Iq2 Ir2)Rp2 + Ip2 Ir2 Ir3 - Ip3 Ir2 Ir3
+
2 2
(Ip2 Iq3 - Ip3 Iq2)Ir2 + %E Ip2 Ir2
*
2
Rq1
+
2 2 2
(- Iq1 Iq2 Ir2 + (Iq2 + %E )Ir1)Ir3 + Iq1 Iq3 Ir2
+
2
(- Iq2 Iq3 Ir1 + %E Iq1)Ir2
*
Rp2
+
3 2
- %E Ir2 Ir3 - 2 %E Iq2 Ir2 Ir3
+
2 2 3
(- %E Iq3 Ir2 + (- %E Ip3 Ir1 - 2 %E Iq2 - %E Ip2 Iq1 - %E )Ir2)Ir3
+
2
- %E Iq2 Iq3 Ir2
+
3 3
(- %E Ip3 Iq2 Ir1 - %E Iq2 + (- %E Ip2 Iq1 - %E )Iq2)Ir2
*
Rq1
+
3
Iq1 Iq2 Ir2 Ir3
+
2 2 2
- Iq1 Iq3 Ir2 + (- Iq2 Iq3 Ir1 + 2 Iq1 Iq2 + Ip2 Iq1 )Ir2
+
3 2
(- Iq2 - %E Iq2)Ir1
*
2
Ir3
+
2 2 2
(Iq3 Ir1 - 2 Iq1 Iq2 Iq3 - Ip3 Iq1 )Ir2
+
2 3
((- 2 Ip2 Iq1 + %E )Iq3 + Ip3 Iq1 Iq2)Ir1 + Iq1 Iq2
+
2
Ip2 Iq1 Iq2
*
Ir2
+
4 2 2 2
(- Iq2 + (- Ip2 Iq1 - %E )Iq2 - %E Ip2 Iq1)Ir1
*
Ir3
+
2 2 2 2
((Iq2 Iq3 + Ip3 Iq1 Iq3)Ir1 - Iq1 Iq2 Iq3 - Ip3 Iq1 Iq2)Ir2
+
2 2
(Ip2 Iq3 - Ip3 Iq2 Iq3)Ir1
+
3 2 2 2
((Iq2 + (- Ip2 Iq1 + %E )Iq2)Iq3 + 2 Ip3 Iq1 Iq2 + %E Ip3 Iq1)Ir1
*
Ir2
+
2 2 3 2 2
((Ip2 Iq2 + %E Ip2)Iq3 - Ip3 Iq2 - %E Ip3 Iq2)Ir1
/
2
Iq2 Ir1 Rr3 + (Iq1 Ir3 - Iq3 Ir1 + Iq1 Iq2)Rr2 + (- Iq2 Ir3 - Iq2 )Rr1
+
- Ir1 Ir2 Rq3 - Iq2 Ir1 Rq2 + (Ir2 Ir3 + Iq2 Ir2)Rq1
Type: Fraction(Polynomial(Complex(Integer)))
fricas
factor C
(46)
2
(Iq1 Ir3 Rq2 - Iq2 Ir3 Rq1 - %E Iq1 Ir3)Rr2 + Iq2 Ir1 Rq2
+
((Ir2 Ir3 + Ip2 Ir1)Rq1 + Iq1 Ir1 Rp2 - 2 %E Iq2 Ir1)Rq2
+
(- Iq2 Ir1 Rp2 - %E Ir2 Ir3 - %E Ip2 Ir1)Rq1 - %E Iq1 Ir1 Rp2
+
3 2
Iq1 Iq2 Ir2 Ir3 + (Iq2 + (Ip2 Iq1 + %E )Iq2)Ir1
*
2
Rr3
+
(- Iq1 Ir3 Rq3 + Iq1 Iq3 Rq2 + (Iq3 Ir3 - Iq2 Iq3)Rq1 - %E Iq1 Iq3)
*
2
Rr2
+
Iq2 Ir3 Rq3 + (- Iq3 Ir3 + Ip3 Iq1)Rq2 - Ip3 Iq2 Rq1
+
%E Iq3 Ir3 - %E Ip3 Iq1
*
Rr1
+
(- Ir1 Ir3 + Iq1 Ir2 - 2 Iq2 Ir1)Rq2
+
(- Iq2 Ir2 - Ip2 Ir1)Rq1 - Iq1 Ir1 Rp2 + %E Ir1 Ir3
+
- %E Iq1 Ir2 + 2 %E Iq2 Ir1
*
Rq3
+
2
(- Iq3 Ir1 + Iq1 Iq2)Rq2
+
2
(2 Iq2 Ir3 + Iq3 Ir2 - Ip3 Ir1 + Ip2 Iq1)Rq1 + Iq1 Rp2
+
- 2 %E Iq1 Ir3 + 2 %E Iq3 Ir1 - 2 %E Iq1 Iq2
*
Rq2
+
2
Ip2 Ir3 Rq1
+
((Iq3 Ir1 - Iq1 Iq2)Rp2 - %E Iq3 Ir2 + %E Ip3 Ir1 - %E Ip2 Iq1)
*
Rq1
+
2
- %E Iq1 Rp2
+
2 2 2
(- Iq2 Iq3 Ir1 + 2 Iq1 Iq2 + Ip2 Iq1 + 2 %E Iq1)Ir3
+
Iq1 Iq2 Iq3 Ir2
+
2 2 3
((- 3 Iq2 - Ip2 Iq1 - %E )Iq3 - Ip3 Iq1 Iq2)Ir1 + Iq1 Iq2
+
2 2
(Ip2 Iq1 + %E Iq1)Iq2
*
Rr2
+
(- Ir2 Ir3 - Ip2 Ir1)Rq2 + Iq2 Ir1 Rp2 + %E Ir2 Ir3
+
%E Ip2 Ir1
*
Rq3
+
2 2
(- 2 Iq2 Ir3 - Iq2 )Rq2
+
(- Ip2 Ir3 + Ip3 Ir2 - Ip2 Iq2)Rq1
+
2
(- Iq1 Ir3 - Iq3 Ir1 - Iq1 Iq2)Rp2 + 4 %E Iq2 Ir3 + 2 %E Iq2
*
Rq2
+
2
((Iq2 Ir3 + Iq2 )Rp2 + %E Ip2 Ir3 - %E Ip3 Ir2 + %E Ip2 Iq2)Rq1
+
(%E Iq1 Ir3 + %E Iq3 Ir1 + %E Iq1 Iq2)Rp2
+
3 2
(- Iq2 Iq3 Ir2 - 2 Iq2 + (- Ip2 Iq1 - 2 %E )Iq2)Ir3
+
4 2 2
Ip3 Iq1 Iq2 Ir2 - Ip2 Iq2 Iq3 Ir1 - Iq2 + (- Ip2 Iq1 - %E )Iq2
*
Rr1
+
2 2 2
- Ir1 Ir2 Rq2 + (Ir2 Rq1 - Ir1 Rp2 + 2 %E Ir1 Ir2)Rq2
+
2 2
(Ir1 Ir2 Rp2 - %E Ir2 )Rq1 + %E Ir1 Rp2
+
2 2
(- Iq1 Ir2 - Iq2 Ir1 Ir2)Ir3 + Iq1 Iq2 Ir2
+
2 2 2
(- 3 Iq2 - Ip2 Iq1 - %E )Ir1 Ir2 - Ip2 Iq2 Ir1
*
Rq3
+
3
- Iq2 Ir1 Rq2
+
2
((Iq2 Ir2 - Ip2 Ir1)Rq1 - Iq1 Ir1 Rp2 + %E Iq2 Ir1)Rq2
+
2
Ip2 Ir2 Rq1
+
(Ir1 Ir3 + Iq1 Ir2 + Iq2 Ir1)Rp2 - 2 %E Ir2 Ir3
+
- 2 %E Iq2 Ir2
*
Rq1
+
((Iq3 Ir1 - 2 Iq1 Iq2)Ir2 - Ip2 Iq1 Ir1)Ir3
+
2
(2 Iq2 Iq3 + Ip3 Iq1)Ir1 Ir2 + Ip2 Iq3 Ir1
+
3 2
(- Iq2 + (- Ip2 Iq1 + %E )Iq2)Ir1
*
Rq2
+
2
((- Ir2 Ir3 - Iq2 Ir2)Rp2 - %E Ip2 Ir2)Rq1
+
(- %E Ir1 Ir3 - %E Iq1 Ir2 + %E Iq2 Ir1)Rp2
+
2 2 2
(Iq3 Ir2 + (2 Iq2 + 2 %E )Ir2 + Ip2 Iq2 Ir1)Ir3
+
3 2
((Ip2 Iq3 - Ip3 Iq2)Ir1 + Iq2 + (Ip2 Iq1 + %E )Iq2)Ir2
+
2
%E Ip2 Ir1
*
Rq1
+
2 2
(- Iq1 Ir2 + Iq1 Iq2 Ir1)Ir3 + Iq1 Iq3 Ir1 Ir2 - Iq2 Iq3 Ir1
+
2
%E Iq1 Ir1
*
Rp2
+
(- %E Iq3 Ir1 Ir2 + %E Ip2 Iq1 Ir1)Ir3
+
2
(- 2 %E Iq2 Iq3 - %E Ip3 Iq1)Ir1 Ir2 - %E Ip2 Iq3 Ir1
+
3 3
(- %E Iq2 + (- %E Ip2 Iq1 - %E )Iq2)Ir1
*
Rr3
+
2 3
(- Iq1 Iq3 Rq3 + Iq3 Rq1)Rr2
+
2 2
((Iq2 Iq3 - Ip3 Iq1)Rq3 - Iq3 Rq2 + Ip3 Iq3 Rq1 + %E Iq3 )Rr1
+
2
(Ir1 Ir3 - Iq1 Ir2 + Iq2 Ir1)Rq3
+
(Iq3 Ir1 - Iq1 Iq2)Rq2
+
2 2
(- Ir3 - 2 Iq2 Ir3 + Iq3 Ir2 + Ip3 Ir1 - Iq2 - Ip2 Iq1)Rq1
+
2
- Iq1 Rp2 + %E Iq1 Ir3 - %E Iq3 Ir1 + %E Iq1 Iq2
*
Rq3
+
((- Iq3 Ir3 + Iq2 Iq3)Rq1 - %E Iq1 Iq3)Rq2
+
2 2
(- Ip3 Ir3 + Ip2 Iq3 - Ip3 Iq2)Rq1 + Iq1 Iq3 Rp2 Rq1 - Iq1 Iq3 Ir3
+
2 2
(Iq3 Ir1 - 3 Iq1 Iq2 Iq3 - Ip3 Iq1 )Ir3
+
2 2 2 2
(2 Iq2 Iq3 + Ip3 Iq1 Iq3)Ir1 + (- Iq1 Iq2 + %E Iq1)Iq3 - Ip3 Iq1 Iq2
*
2
Rr2
+
2
(Ip3 Iq2 Rq3 - Ip3 Iq3 Rq2 + %E Ip3 Iq3)Rr1
+
2
(Iq2 Ir2 + Ip2 Ir1)Rq3
+
2 2
(Ir3 + 2 Iq2 Ir3 - 2 Iq3 Ir2 + 2 Iq2 )Rq2 - Ip2 Ir3 Rq1
+
2
(Iq1 Ir3 + 2 Iq1 Iq2)Rp2 - %E Ir3 - 3 %E Iq2 Ir3
+
2
2 %E Iq3 Ir2 - 2 %E Iq2
*
Rq3
+
2
(Iq3 Ir3 - Iq2 Iq3)Rq2
+
(Ip3 Ir3 - Ip2 Iq3 + 2 Ip3 Iq2)Rq1 - Iq1 Iq3 Rp2 - %E Iq3 Ir3
+
2 %E Iq2 Iq3 - %E Ip3 Iq1
*
Rq2
+
(- Iq3 Ir3 - Iq2 Iq3)Rp2 - %E Ip3 Ir3 + %E Ip2 Iq3
+
- %E Ip3 Iq2
*
Rq1
+
2
%E Iq1 Iq3 Rp2 + Iq2 Iq3 Ir3
+
2 2
((3 Iq2 - Ip2 Iq1)Iq3 + Ip3 Iq1 Iq2)Ir3 - Iq2 Iq3 Ir2
+
2 3 2 2
Ip2 Iq3 Ir1 + (Iq2 + (- Ip2 Iq1 - %E )Iq2)Iq3 + 2 Ip3 Iq1 Iq2
+
2
%E Ip3 Iq1
*
Rr1
+
2 2
(Ir1 Ir2 Rq2 + Ir1 Rp2 - %E Ir1 Ir2)Rq3
+
2
Iq2 Ir1 Rq2
+
(- Ir2 Ir3 + Ip2 Ir1)Rq1 + Iq1 Ir1 Rp2 + %E Ir1 Ir3
+
- %E Iq1 Ir2
*
Rq2
+
((- 2 Ir1 Ir3 - Iq2 Ir1)Rp2 + %E Ir2 Ir3 + %E Iq2 Ir2)Rq1
+
2 2 2
Iq2 Ir1 Ir3 + (- Iq1 Iq2 Ir2 - %E Ir1)Ir3 - Iq1 Iq3 Ir2
+
2 2
(2 Iq2 Iq3 Ir1 + %E Iq1)Ir2 + Ip3 Iq2 Ir1
+
3 2
(- Iq2 + (- Ip2 Iq1 - %E )Iq2)Ir1
*
Rq3
+
2
(- Iq2 Ir3 Rq1 + %E Iq3 Ir1 - %E Iq1 Iq2)Rq2
+
2
- Ip2 Ir3 Rq1
+
(- Iq1 Ir3 Rp2 - %E Iq3 Ir2 + %E Ip3 Ir1 - %E Ip2 Iq1)Rq1
+
2 3 2
- %E Iq1 Rp2 + Iq1 Ir3 + (- Iq3 Ir1 + 2 Iq1 Iq2)Ir3
+
2 2
(Iq1 Iq3 Ir2 + Ip3 Iq1 Ir1 + %E Iq1)Ir3 - Iq3 Ir1 Ir2
+
2 2 2
- Ip3 Iq3 Ir1 + ((2 Iq2 - 2 %E )Iq3 + 2 Ip3 Iq1 Iq2)Ir1
+
2
2 %E Iq1 Iq2
*
Rq2
+
2 2
(Ir3 + Iq2 Ir3)Rp2 Rq1
+
3 2 2
(%E Iq1 Ir3 - %E Iq3 Ir1 + %E Iq1 Iq2)Rp2 - Iq2 Ir3 - 2 Iq2 Ir3
+
3 2 2
(- Iq2 Iq3 Ir2 - Ip3 Iq2 Ir1 - Iq2 - Ip2 Iq1 Iq2)Ir3 + Iq3 Ir2
+
2 2 2 2
%E Iq3 Ir2 + (2 Ip2 Iq2 Iq3 - 2 Ip3 Iq2 - %E Ip3)Ir1 + %E Ip2 Iq1
*
Rq1
+
2 2 2 2 2 2 3
(Iq1 Ir3 - 2 Iq1 Iq3 Ir1 Ir3 + Iq3 Ir1 + %E Iq1 )Rp2 - %E Iq1 Ir3
+
2
(%E Iq3 Ir1 - 2 %E Iq1 Iq2)Ir3
+
2
- %E Iq1 Iq3 Ir2 + (%E Iq2 Iq3 - %E Ip3 Iq1)Ir1 - 2 %E Iq1 Iq2
+
2 3
- %E Ip2 Iq1 - %E Iq1
*
Ir3
+
2 2
(%E Iq3 Ir1 - %E Iq1 Iq2 Iq3)Ir2 + %E Ip3 Iq3 Ir1
+
2 3 3
((%E Iq2 + %E Ip2 Iq1 + %E )Iq3 - %E Ip3 Iq1 Iq2)Ir1 - %E Iq1 Iq2
+
2 3
(- %E Ip2 Iq1 - %E Iq1)Iq2
*
Rr2
+
2
(Ip2 Ir3 - Ip3 Ir2 + Ip2 Iq2)Rq2 + (- Iq2 Ir3 - Iq2 )Rp2
+
- %E Ip2 Ir3 + %E Ip3 Ir2 - %E Ip2 Iq2
*
Rq3
+
2
- Ip3 Iq2 Rq2 + ((Iq3 Ir3 + Iq2 Iq3)Rp2 + 2 %E Ip3 Iq2)Rq2
+
(- %E Iq3 Ir3 - %E Iq2 Iq3)Rp2 + Ip2 Iq2 Iq3 Ir3 - Ip3 Iq2 Iq3 Ir2
+
2 3 2
Ip2 Iq2 Iq3 - Ip3 Iq2 - %E Ip3 Iq2
*
2
Rr1
+
2 2 2
(- Ir2 Rq2 - Ir1 Ir2 Rp2 + %E Ir2 )Rq3
+
2
(Ir2 Ir3 - Iq2 Ir2)Rq2
+
- Ip2 Ir2 Rq1 + (Ir1 Ir3 - Iq1 Ir2)Rp2 - %E Ir2 Ir3
+
2 %E Iq2 Ir2 + %E Ip2 Ir1
*
Rq2
+
((Ir2 Ir3 + Iq2 Ir2)Rp2 + %E Ip2 Ir2)Rq1
+
2
(- %E Ir1 Ir3 + %E Iq1 Ir2 - %E Iq2 Ir1)Rp2 + Iq2 Ir2 Ir3
+
2
((3 Iq2 + Ip2 Iq1)Ir2 + Ip2 Iq2 Ir1)Ir3
+
2 3 2
(- Iq2 Iq3 - Ip3 Iq1)Ir2 + (Iq2 + (Ip2 Iq1 - %E )Iq2)Ir2
+
2
- %E Ip2 Ir1
*
Rq3
+
3 2 2
Iq2 Ir3 Rq2 + (Ip2 Ir3 Rq1 + Iq1 Ir3 Rp2 - %E Iq2 Ir3 + %E Iq2 )Rq2
+
2
((- Ir3 - Iq2 Ir3)Rp2 - %E Ip2 Ir3 - %E Ip3 Ir2 + %E Ip2 Iq2)Rq1
+
(- %E Iq1 Ir3 + %E Iq3 Ir1 + %E Iq1 Iq2)Rp2
+
2
(- Iq3 Ir2 + Ip2 Iq1)Ir3
+
3
(- 2 Iq2 Iq3 - Ip3 Iq1)Ir2 - Ip2 Iq3 Ir1 + Iq2
+
2
(Ip2 Iq1 - %E )Iq2
*
Ir3
+
2 2 2
(- 2 Iq2 Iq3 - 2 Ip3 Iq1 Iq2)Ir2 - 2 %E Iq2
*
Rq2
+
2 2 2
(%E Ir3 - %E Iq2 )Rp2 - Ip2 Iq2 Ir3
+
2
(- Ip2 Iq3 + Ip3 Iq2)Ir2 Ir3 + Ip3 Iq3 Ir2
+
2 2 2
(- 2 Ip2 Iq2 Iq3 + 2 Ip3 Iq2 + %E Ip3)Ir2 - %E Ip2 Iq2
*
Rq1
+
2 2
- Iq1 Iq2 Ir3 + (Iq1 Iq3 Ir2 + Iq2 Iq3 Ir1)Ir3 - Iq3 Ir1 Ir2
+
2 2
- %E Iq3 Ir1 - %E Iq1 Iq2
*
Rp2
+
2
(%E Iq3 Ir2 - %E Ip2 Iq1)Ir3
+
3
(3 %E Iq2 Iq3 + %E Ip3 Iq1)Ir2 + %E Ip2 Iq3 Ir1 + %E Iq2
+
3
%E Iq2
*
Ir3
+
2 4
(2 %E Iq2 Iq3 + %E Ip3 Iq1 Iq2)Ir2 + %E Ip2 Iq2 Iq3 Ir1 + %E Iq2
+
3 2
(%E Ip2 Iq1 + %E )Iq2
*
Rr1
+
2 3 2 2 2
(Ir1 Ir2 Ir3 - Iq1 Ir2 + 2 Iq2 Ir1 Ir2 + Ip2 Ir1 Ir2)Rq3
+
2
%E Ir1 Ir2 Rq2
+
2 2 2 2
- %E Ir2 Rq1 + %E Ir1 Rp2 - Ir1 Ir2 Ir3 + Iq1 Ir2 Ir3
+
2 2 2 2
(- Iq3 Ir1 - Iq1 Iq2)Ir2 + (- Ip3 Ir1 + (2 Iq2 - 2 %E )Ir1)Ir2
+
2
Ip2 Iq2 Ir1
*
Rq2
+
2 2 2
- %E Ir1 Ir2 Rp2 - Ir2 Ir3 + (- 3 Iq2 Ir2 - 2 Ip2 Ir1 Ir2)Ir3
+
3 2 2 2
Iq3 Ir2 + (Ip3 Ir1 - Iq2 - Ip2 Iq1 + %E )Ir2
*
Rq1
+
2 2 2 2 2
(- Iq1 Ir2 + 2 Iq1 Iq2 Ir1 Ir2 + (- Iq2 - %E )Ir1 )Rp2
+
2 2
%E Ir1 Ir2 Ir3 + %E Iq2 Ir1 Ir2 Ir3 + %E Iq3 Ir1 Ir2
+
2 2 3
(%E Ip3 Ir1 + (%E Iq2 + %E Ip2 Iq1 + %E )Ir1)Ir2
*
Rq3
+
3
%E Iq2 Ir1 Rq2
+
2
(- %E Iq2 Ir2 + %E Ip2 Ir1)Rq1 + %E Iq1 Ir1 Rp2 - Iq2 Ir1 Ir3
+
2 2
(Iq1 Iq2 Ir2 - Iq2 Ir1)Ir3 - Iq2 Iq3 Ir1 Ir2 - Ip3 Iq2 Ir1
+
2
- 2 %E Iq2 Ir1
*
2
Rq2
+
2
- %E Ip2 Ir2 Rq1
+
3
(- %E Ir1 Ir3 - %E Iq1 Ir2 - %E Iq2 Ir1)Rp2 + Ir2 Ir3
+
2 2
2 Iq2 Ir2 Ir3 + ((Ip3 Ir1 + Ip2 Iq1 + %E )Ir2 - Ip2 Iq2 Ir1)Ir3
+
2 2
Iq2 Iq3 Ir2 + ((- Ip2 Iq3 + 2 Ip3 Iq2)Ir1 + 2 %E Iq2)Ir2
+
2
- %E Ip2 Ir1
*
Rq1
+
2 2
(Iq1 Ir2 - Iq1 Iq2 Ir1)Ir3 - Iq1 Iq3 Ir1 Ir2 + Iq2 Iq3 Ir1
+
2
- %E Iq1 Ir1
*
Rp2
+
2
2 %E Iq2 Ir1 Ir3
+
2
(- %E Iq3 Ir1 Ir2 + (2 %E Iq2 + %E Ip2 Iq1)Ir1)Ir3
+
2
- %E Ip3 Iq1 Ir1 Ir2 + (- %E Ip2 Iq3 + 2 %E Ip3 Iq2)Ir1
+
3 3
(%E Iq2 + (%E Ip2 Iq1 + %E )Iq2)Ir1
*
Rq2
+
2 2
(%E Ir2 Ir3 + %E Iq2 Ir2)Rp2 + Ip2 Ir2 Ir3 - Ip3 Ir2 Ir3
+
2 2
(Ip2 Iq3 - Ip3 Iq2)Ir2 + %E Ip2 Ir2
*
2
Rq1
+
2 2 2
(- Iq1 Iq2 Ir2 + (Iq2 + %E )Ir1)Ir3 + Iq1 Iq3 Ir2
+
2
(- Iq2 Iq3 Ir1 + %E Iq1)Ir2
*
Rp2
+
3 2
- %E Ir2 Ir3 - 2 %E Iq2 Ir2 Ir3
+
2 2 3
(- %E Iq3 Ir2 + (- %E Ip3 Ir1 - 2 %E Iq2 - %E Ip2 Iq1 - %E )Ir2)Ir3
+
2
- %E Iq2 Iq3 Ir2
+
3 3
(- %E Ip3 Iq2 Ir1 - %E Iq2 + (- %E Ip2 Iq1 - %E )Iq2)Ir2
*
Rq1
+
3
Iq1 Iq2 Ir2 Ir3
+
2 2 2
- Iq1 Iq3 Ir2 + (- Iq2 Iq3 Ir1 + 2 Iq1 Iq2 + Ip2 Iq1 )Ir2
+
3 2
(- Iq2 - %E Iq2)Ir1
*
2
Ir3
+
2 2 2
(Iq3 Ir1 - 2 Iq1 Iq2 Iq3 - Ip3 Iq1 )Ir2
+
2 3
((- 2 Ip2 Iq1 + %E )Iq3 + Ip3 Iq1 Iq2)Ir1 + Iq1 Iq2
+
2
Ip2 Iq1 Iq2
*
Ir2
+
4 2 2 2
(- Iq2 + (- Ip2 Iq1 - %E )Iq2 - %E Ip2 Iq1)Ir1
*
Ir3
+
2 2 2 2
((Iq2 Iq3 + Ip3 Iq1 Iq3)Ir1 - Iq1 Iq2 Iq3 - Ip3 Iq1 Iq2)Ir2
+
2 2
(Ip2 Iq3 - Ip3 Iq2 Iq3)Ir1
+
3 2 2 2
((Iq2 + (- Ip2 Iq1 + %E )Iq2)Iq3 + 2 Ip3 Iq1 Iq2 + %E Ip3 Iq1)Ir1
*
Ir2
+
2 2 3 2 2
((Ip2 Iq2 + %E Ip2)Iq3 - Ip3 Iq2 - %E Ip3 Iq2)Ir1
/
2
Iq2 Ir1 Rr3 + (Iq1 Ir3 - Iq3 Ir1 + Iq1 Iq2)Rr2 + (- Iq2 Ir3 - Iq2 )Rr1
+
- Ir1 Ir2 Rq3 - Iq2 Ir1 Rq2 + (Ir2 Ir3 + Iq2 Ir2)Rq1
Type: Factored(Fraction(Polynomial(Complex(Integer))))
fricas
C0:=zerosOf(C);
Type: List(Expression(Complex(Integer)))
fricas
#C0
(48) 3
fricas
imag(C0.1)
(49) 0
Type: Expression(Integer)
fricas
imag(C0.2)
(50) 0
Type: Expression(Integer)
fricas
imag(C0.3)
(51) 0
Type: Expression(Integer)
Given an operator  , one must find the tensor
, one must find the tensor 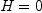 for unknown manifold of hermitian isomorphisms
for unknown manifold of hermitian isomorphisms 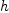 .
.
fricas
h:Matrix CC:=matrix [[Ra, complex(Rb,Ib), complex(Rc,Ic)], _
[complex(Rb,-Ib),Re, complex(Rd,Id)], _
[complex(Rc,-Ic),complex(Rd,-Id),Rf ]]
+ Ra Rb + Ib %i Rc + Ic %i+
| |
(52) |Rb - Ib %i Re Rd + Id %i|
| |
+Rc - Ic %i Rd - Id %i Rf +
Type: Matrix(Complex(Fraction(Polynomial(Integer))))
fricas
test(h = htranspose h)
(53) true
Type: Boolean
fricas
H:=htranspose(rho)*h-h*rho
(54)
[
[(- 2 Ic Rp3 - 2 Ib Rp2 - 2 Ip3 Rc - 2 Ip2 Rb - 2 Ip1 Ra)%i,
- Rc Rq3 - Rb Rq2 - Ra Rq1 + Rd Rp3 + Re Rp2 + Rb Rp1 + Ic Iq3 + Ib Iq2
+
- Id Ip3 + Ib Ip1
+
- Ic Rq3 - Ib Rq2 - Id Rp3 + Ib Rp1 - Ip2 Re - Ip3 Rd - Iq3 Rc
+
(- Iq2 - Ip1)Rb - Iq1 Ra
*
%i
,
- Rc Rr3 - Rb Rr2 - Ra Rr1 + Rf Rp3 + Rd Rp2 + Rc Rp1 + Ic Ir3 + Ib Ir2
+
Id Ip2 + Ic Ip1
+
- Ic Rr3 - Ib Rr2 + Id Rp2 + Ic Rp1 - Ip3 Rf - Ip2 Rd
+
(- Ir3 - Ip1)Rc - Ir2 Rb - Ir1 Ra
*
%i
]
,
[
Rc Rq3 + Rb Rq2 + Ra Rq1 - Rd Rp3 - Re Rp2 - Rb Rp1 - Ic Iq3 - Ib Iq2
+
Id Ip3 - Ib Ip1
+
- Ic Rq3 - Ib Rq2 - Id Rp3 + Ib Rp1 - Ip2 Re - Ip3 Rd - Iq3 Rc
+
(- Iq2 - Ip1)Rb - Iq1 Ra
*
%i
,
(- 2 Id Rq3 + 2 Ib Rq1 - 2 Iq2 Re - 2 Iq3 Rd - 2 Iq1 Rb)%i,
- Rd Rr3 - Re Rr2 - Rb Rr1 + Rf Rq3 + Rd Rq2 + Rc Rq1 + Id Ir3 - Ib Ir1
+
Id Iq2 + Ic Iq1
+
- Id Rr3 + Ib Rr1 + Id Rq2 + Ic Rq1 - Iq3 Rf - Ir2 Re
+
(- Ir3 - Iq2)Rd - Iq1 Rc - Ir1 Rb
*
%i
]
,
[
Rc Rr3 + Rb Rr2 + Ra Rr1 - Rf Rp3 - Rd Rp2 - Rc Rp1 - Ic Ir3 - Ib Ir2
+
- Id Ip2 - Ic Ip1
+
- Ic Rr3 - Ib Rr2 + Id Rp2 + Ic Rp1 - Ip3 Rf - Ip2 Rd
+
(- Ir3 - Ip1)Rc - Ir2 Rb - Ir1 Ra
*
%i
,
Rd Rr3 + Re Rr2 + Rb Rr1 - Rf Rq3 - Rd Rq2 - Rc Rq1 - Id Ir3 + Ib Ir1
+
- Id Iq2 - Ic Iq1
+
- Id Rr3 + Ib Rr1 + Id Rq2 + Ic Rq1 - Iq3 Rf - Ir2 Re
+
(- Ir3 - Iq2)Rd - Iq1 Rc - Ir1 Rb
*
%i
,
(2 Id Rr2 + 2 Ic Rr1 - 2 Ir3 Rf - 2 Ir2 Rd - 2 Ir1 Rc)%i]
]
Type: Matrix(Complex(Fraction(Polynomial(Integer))))
We wish to find expressions for 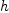 in terms of the components of
in terms of the components of
 . To do this we will determine how the components of
. To do this we will determine how the components of 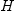 depend
on the components of
depend
on the components of 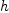 .
.
fricas
K:=concat( map(x+->[real x, imag x], concat(H::List List ?)))::List Polynomial Integer
(55)
[0, - 2 Ic Rp3 - 2 Ib Rp2 - 2 Ip3 Rc - 2 Ip2 Rb - 2 Ip1 Ra,
- Rc Rq3 - Rb Rq2 - Ra Rq1 + Rd Rp3 + Re Rp2 + Rb Rp1 + Ic Iq3 + Ib Iq2
+
- Id Ip3 + Ib Ip1
,
- Ic Rq3 - Ib Rq2 - Id Rp3 + Ib Rp1 - Ip2 Re - Ip3 Rd - Iq3 Rc
+
(- Iq2 - Ip1)Rb - Iq1 Ra
,
- Rc Rr3 - Rb Rr2 - Ra Rr1 + Rf Rp3 + Rd Rp2 + Rc Rp1 + Ic Ir3 + Ib Ir2
+
Id Ip2 + Ic Ip1
,
- Ic Rr3 - Ib Rr2 + Id Rp2 + Ic Rp1 - Ip3 Rf - Ip2 Rd + (- Ir3 - Ip1)Rc
+
- Ir2 Rb - Ir1 Ra
,
Rc Rq3 + Rb Rq2 + Ra Rq1 - Rd Rp3 - Re Rp2 - Rb Rp1 - Ic Iq3 - Ib Iq2
+
Id Ip3 - Ib Ip1
,
- Ic Rq3 - Ib Rq2 - Id Rp3 + Ib Rp1 - Ip2 Re - Ip3 Rd - Iq3 Rc
+
(- Iq2 - Ip1)Rb - Iq1 Ra
,
0, - 2 Id Rq3 + 2 Ib Rq1 - 2 Iq2 Re - 2 Iq3 Rd - 2 Iq1 Rb,
- Rd Rr3 - Re Rr2 - Rb Rr1 + Rf Rq3 + Rd Rq2 + Rc Rq1 + Id Ir3 - Ib Ir1
+
Id Iq2 + Ic Iq1
,
- Id Rr3 + Ib Rr1 + Id Rq2 + Ic Rq1 - Iq3 Rf - Ir2 Re + (- Ir3 - Iq2)Rd
+
- Iq1 Rc - Ir1 Rb
,
Rc Rr3 + Rb Rr2 + Ra Rr1 - Rf Rp3 - Rd Rp2 - Rc Rp1 - Ic Ir3 - Ib Ir2
+
- Id Ip2 - Ic Ip1
,
- Ic Rr3 - Ib Rr2 + Id Rp2 + Ic Rp1 - Ip3 Rf - Ip2 Rd + (- Ir3 - Ip1)Rc
+
- Ir2 Rb - Ir1 Ra
,
Rd Rr3 + Re Rr2 + Rb Rr1 - Rf Rq3 - Rd Rq2 - Rc Rq1 - Id Ir3 + Ib Ir1
+
- Id Iq2 - Ic Iq1
,
- Id Rr3 + Ib Rr1 + Id Rq2 + Ic Rq1 - Iq3 Rf - Ir2 Re + (- Ir3 - Iq2)Rd
+
- Iq1 Rc - Ir1 Rb
,
0, 2 Id Rr2 + 2 Ic Rr1 - 2 Ir3 Rf - 2 Ir2 Rd - 2 Ir1 Rc]
Type: List(Polynomial(Integer))
fricas
--K2:=groebner(K)
J:=jacobian(select(x+->x~=0,K), [Ra,Rb,Ib,Rc,Ic,Rd,Id,Re,Rf]::List Symbol)
(56)
[[- 2 Ip1, - 2 Ip2, - 2 Rp2, - 2 Ip3, - 2 Rp3, 0, 0, 0, 0],
[- Rq1, - Rq2 + Rp1, Iq2 + Ip1, - Rq3, Iq3, Rp3, - Ip3, Rp2, 0],
[- Iq1, - Iq2 - Ip1, - Rq2 + Rp1, - Iq3, - Rq3, - Ip3, - Rp3, - Ip2, 0],
[- Rr1, - Rr2, Ir2, - Rr3 + Rp1, Ir3 + Ip1, Rp2, Ip2, 0, Rp3],
[- Ir1, - Ir2, - Rr2, - Ir3 - Ip1, - Rr3 + Rp1, - Ip2, Rp2, 0, - Ip3],
[Rq1, Rq2 - Rp1, - Iq2 - Ip1, Rq3, - Iq3, - Rp3, Ip3, - Rp2, 0],
[- Iq1, - Iq2 - Ip1, - Rq2 + Rp1, - Iq3, - Rq3, - Ip3, - Rp3, - Ip2, 0],
[0, - 2 Iq1, 2 Rq1, 0, 0, - 2 Iq3, - 2 Rq3, - 2 Iq2, 0],
[0, - Rr1, - Ir1, Rq1, Iq1, - Rr3 + Rq2, Ir3 + Iq2, - Rr2, Rq3],
[0, - Ir1, Rr1, - Iq1, Rq1, - Ir3 - Iq2, - Rr3 + Rq2, - Ir2, - Iq3],
[Rr1, Rr2, - Ir2, Rr3 - Rp1, - Ir3 - Ip1, - Rp2, - Ip2, 0, - Rp3],
[- Ir1, - Ir2, - Rr2, - Ir3 - Ip1, - Rr3 + Rp1, - Ip2, Rp2, 0, - Ip3],
[0, Rr1, Ir1, - Rq1, - Iq1, Rr3 - Rq2, - Ir3 - Iq2, Rr2, - Rq3],
[0, - Ir1, Rr1, - Iq1, Rq1, - Ir3 - Iq2, - Rr3 + Rq2, - Ir2, - Iq3],
[0, 0, 0, - 2 Ir1, 2 Rr1, - 2 Ir2, 2 Rr2, 0, - 2 Ir3]]
Type: Matrix(Polynomial(Integer))
The null space (kernel) of the Jacobian
fricas
J2:=map(x+->eval(eval(eval(x,s1),s2),s3),J);
Type: Matrix(Fraction(Polynomial(Integer)))
fricas
nrows(J2),ncols(J2)
(58) [15, 9]
Type: Tuple(PositiveInteger
?)
fricas
binomial(nrows(J2),ncols(J2))
(59) 5005
SandBoxHermitianIsomorphisms4