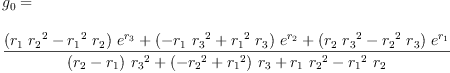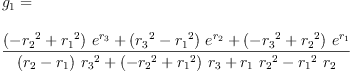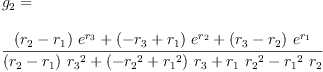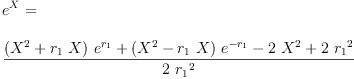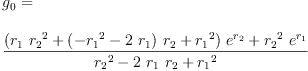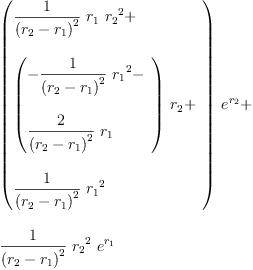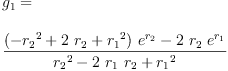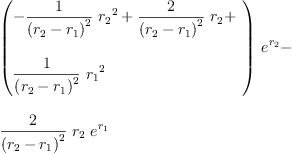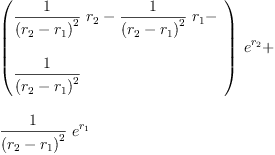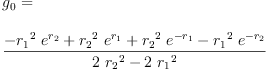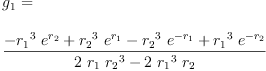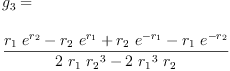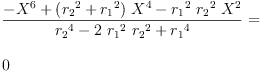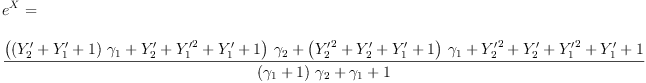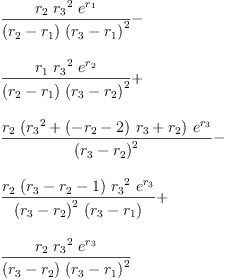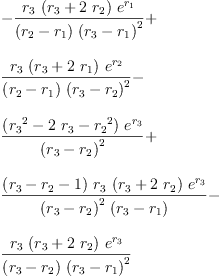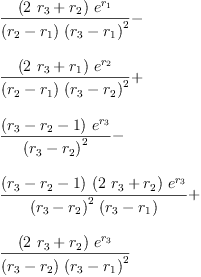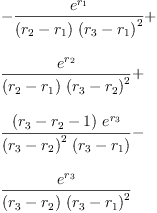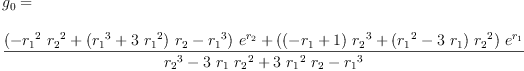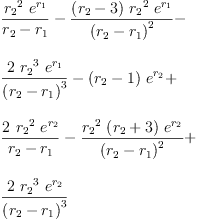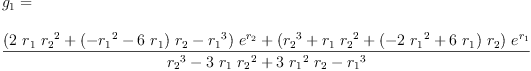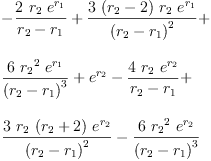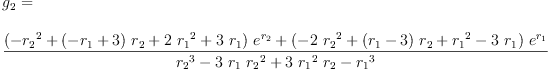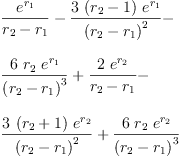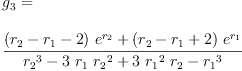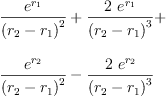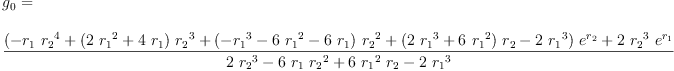MathAction SandBoxExpOfEnd

Topics

FrontPage
- SandBox
  - SandBoxExpOfEnd <-- You are here.

SandBoxCollect

Exponential of endomorphism with minimal polynomial

First define some needed operations

Sum and product

fricas

sum(x)==reduce(+,x)

Type: Void

fricas

product(x)==reduce(*,x,1)

Type: Void

Collect terms in x with given factor k.

fricas

QF==>PolynomialCategoryQuotientFunctions(IndexedExponents Kernel Expression Integer,_
                                         Kernel Expression Integer,_
                                         Integer,_
                                         SparseMultivariatePolynomial(Integer,Kernel Expression Integer),_
                                         Expression Integer)

Type: Void

fricas

--collect(x:Expression Integer,k:Kernel Expression Integer):Expression Integer ==
collect(x,k) ==
  n1:=univariate(x::Expression Integer,k::Kernel Expression Integer)$QF
  n2:=(leadingMonomial numer n1)/(denom n1)
  n3:=multivariate(n2,k::Kernel Expression Integer)$QF
  n4:=factor(numer n3)/factor(denom n3)

Type: Void

fricas

--
collector(x:Expression Integer,k:Expression Integer):List Expression Integer ==
  s1:=solve(%k=k,variables(k)(1))
  x2:=eval(collect(eval(x,s1),%k::Expression Integer::Kernel Expression Integer)::Expression Integer,%k=k)
  x2=0 => []
  concat(x2,collector(x-x2,k))

   Function declaration collector : (Expression(Integer), Expression(
      Integer)) -> List(Expression(Integer)) has been added to 
      workspace.

Type: Void

fricas

--
collector((r2-r1+1)^3,(r2-r1)::Expression Integer)

fricas

Compiling function collect with type (Expression(Integer), Kernel(
      Expression(Integer))) -> Fraction(Factored(
      SparseMultivariatePolynomial(Integer,Kernel(Expression(Integer)))
      ))

fricas

Compiling function collector with type (Expression(Integer), 
      Expression(Integer)) -> List(Expression(Integer))

$\label{eq1}\begin{array}{@{}l} \displaystyle \left[{{{r 2}^{3}}-{3 \ r 1 \ {{r 2}^{2}}}+{3 \ {{r 1}^{2}}\ r 2}-{{r 1}^{3}}}, \:{{3 \ {{r 2}^{2}}}-{6 \ r 1 \ r 2}+{3 \ {{r 1}^{2}}}}, \: \right. \ \ \displaystyle \left.{{3 \ r 2}-{3 \ r 1}}, \: 1 \right]$

(1)

Type: List(Expression(Integer))

fricas

test(sum % = (r2-r1+1)^3)

fricas

Compiling function sum with type List(Expression(Integer)) -> 
      Expression(Integer)

$\label{eq2} \mbox{\rm true}$

(2)

Type: Boolean

Choose n items from a list. Returns list of size binomial(#a,n) of lists.

fricas

choose(a,n) ==
  j:=[i for i in 1..n]
  r:=[[a(j(i)) for i in 1..n]]
  k:=n
  while k>0 and j(k)+n-k<#a repeat
    j(k):=j(k)+1
    for i in k..n-1 repeat j(i+1):=j(i)+1
    r:=concat(r,[a(j(i)) for i in 1..n])
    k:=n; while j(k)+n-k>=#a and k>1 repeat k:=k-1
  if binomial(#a,n)~=#r then error "error in choose"
  return r

Type: Void

Verification of calculations in the paper

(version date: September 12, 2014)

Parameterizing group-polynomial in terms of the roots of the generator

Minimal polynomial

The Main Result 2.3

The explicit expression for the group-polynomial coefficient functions

fricas

groupPolyCoeff(i) == (-1)^(i+n+1)*sum([exp(r[j])/product([r[j]-r[m] for m in 1..n | j~=m])*f(i,j) for j in 1..n])

Type: Void

fricas

f(i,j) == sum [ product x for x in choose([r[q]::Expression Integer for q in 1..n|q~=j],n-i-1)]

Type: Void

Example (polynomial of degree 1)

fricas

n:=1

$\label{eq3}1$

(3)

Type: PositiveInteger?

fricas

groupPolyCoeff(0)

fricas

Compiling function product with type List(Polynomial(Integer)) -> 
      Polynomial(Integer)

fricas

Compiling function choose with type (List(Expression(Integer)), 
      Integer) -> List(List(Expression(Integer)))

fricas

Compiling function product with type List(Expression(Integer)) -> 
      Expression(Integer)

fricas

Compiling function f with type (NonNegativeInteger, PositiveInteger)
       -> Expression(Integer)

fricas

Compiling function groupPolyCoeff with type NonNegativeInteger -> 
      Expression(Integer)

$\label{eq4}{e}^{r_{1}}$

(4)

Type: Expression(Integer)

Polynomial of degree 2

fricas

n:=2

$\label{eq5}2$

(5)

Type: PositiveInteger?

fricas

eq2_1:= m[X]=(x-r[1])*(x-r[2])

$\label{eq6}{m_{X}}={{{x}^{2}}+{{\left(-{r_{2}}-{r_{1}}\right)}\ x}+{{r_{1}}\ {r_{2}}}}$

(6)

Type: Equation(Polynomial(Integer))

fricas

eq2_2:= exp(X)=g[0]+g[1]*X

$\label{eq7}{{e}^{X}}={{{g_{1}}\ X}+{g_{0}}}$

(7)

Type: Equation(Expression(Integer))

fricas

eq2_3a:= g[0]=groupPolyCoeff(0)

$\label{eq8}{g_{0}}={{-{{r_{1}}\ {{e}^{r_{2}}}}+{{r_{2}}\ {{e}^{r_{1}}}}}\over{{r_{2}}-{r_{1}}}}$

(8)

Type: Equation(Expression(Integer))

fricas

eq2_3b:= g[1]=groupPolyCoeff(1)

fricas

Compiling function f with type (PositiveInteger, PositiveInteger)
       -> Expression(Integer)

fricas

Compiling function groupPolyCoeff with type PositiveInteger -> 
      Expression(Integer)

$\label{eq9}{g_{1}}={{{{e}^{r_{2}}}-{{e}^{r_{1}}}}\over{{r_{2}}-{r_{1}}}}$

(9)

Type: Equation(Expression(Integer))

Example 3.1 (Tri-gonometry)

fricas

eval(eq2_1,[r[2]=-r[1]])

$\label{eq10}{m_{X}}={{{x}^{2}}-{{r_{1}}^{2}}}$

(10)

Type: Equation(Polynomial(Integer))

fricas

eq2_4:= eval(eval(eq2_2,[eq2_3a,eq2_3b]),r[2]=-r[1])

$\label{eq11}{{e}^{X}}={{{{\left(X +{r_{1}}\right)}\ {{e}^{r_{1}}}}+{{\left(- X +{r_{1}}\right)}\ {{e}^{-{r_{1}}}}}}\over{2 \ {r_{1}}}}$

(11)

Type: Equation(Expression(Integer))

fricas

htrigs rhs %

$\label{eq12}{{X \ {\sinh \left({r_{1}}\right)}}+{{r_{1}}\ {\cosh \left({r_{1}}\right)}}}\over{r_{1}}$

(12)

Type: Expression(Integer)

Polynomial of degree 3
fricas
```
n:=3
```
$\label{eq13}3$ (13)

Type: PositiveInteger?

fricas
```
eq3_1:= m[X]=(x-r[1])*(x-r[2])*(x-r[3])
```
$\label{eq14}\begin{array}{@{}l} \displaystyle {m_{X}}={ \begin{array}{@{}l} \displaystyle {{x}^{3}}+{{\left(-{r_{3}}-{r_{2}}-{r_{1}}\right)}\ {{x}^{2}}}+{{\left({{\left({r_{2}}+{r_{1}}\right)}\ {r_{3}}}+{{r_{1}}\ {r_{2}}}\right)}\ x}- \ \ \displaystyle {{r_{1}}\ {r_{2}}\ {r_{3}}}$ (14)

Type: Equation(Polynomial(Integer))

fricas
```
eq3_2:= exp(X)=g[0]+g[1]*X+g[2]*X^2
```
$\label{eq15}{{e}^{X}}={{{g_{2}}\ {{X}^{2}}}+{{g_{1}}\ X}+{g_{0}}}$ (15)

Type: Equation(Expression(Integer))

fricas
```
eq3_3a:= g[0]=groupPolyCoeff(0)
```
$\label{eq16}\begin{array}{@{}l} \displaystyle {g_{0}}={{\left( \begin{array}{@{}l} \displaystyle {{\left({{r_{1}}\ {{r_{2}}^{2}}}-{{{r_{1}}^{2}}\ {r_{2}}}\right)}\ {{e}^{r_{3}}}}+ \ \ \displaystyle {{\left(-{{r_{1}}\ {{r_{3}}^{2}}}+{{{r_{1}}^{2}}\ {r_{3}}}\right)}\ {{e}^{r_{2}}}}+ \ \ \displaystyle {{\left({{r_{2}}\ {{r_{3}}^{2}}}-{{{r_{2}}^{2}}\ {r_{3}}}\right)}\ {{e}^{r_{1}}}}$ (16)

Type: Equation(Expression(Integer))

fricas
```
eq3_3b:= g[1]=groupPolyCoeff(1)
```
$\label{eq17}{g_{1}}={{{{\left(-{{r_{2}}^{2}}+{{r_{1}}^{2}}\right)}\ {{e}^{r_{3}}}}+{{\left({{r_{3}}^{2}}-{{r_{1}}^{2}}\right)}\ {{e}^{r_{2}}}}+{{\left(-{{r_{3}}^{2}}+{{r_{2}}^{2}}\right)}\ {{e}^{r_{1}}}}}\over{{{\left({r_{2}}-{r_{1}}\right)}\ {{r_{3}}^{2}}}+{{\left(-{{r_{2}}^{2}}+{{r_{1}}^{2}}\right)}\ {r_{3}}}+{{r_{1}}\ {{r_{2}}^{2}}}-{{{r_{1}}^{2}}\ {r_{2}}}}}$ (17)

Type: Equation(Expression(Integer))

fricas
```
eq3_3c:= g[2]=groupPolyCoeff(2)
```
$\label{eq18}{g_{2}}={{{{\left({r_{2}}-{r_{1}}\right)}\ {{e}^{r_{3}}}}+{{\left(-{r_{3}}+{r_{1}}\right)}\ {{e}^{r_{2}}}}+{{\left({r_{3}}-{r_{2}}\right)}\ {{e}^{r_{1}}}}}\over{{{\left({r_{2}}-{r_{1}}\right)}\ {{r_{3}}^{2}}}+{{\left(-{{r_{2}}^{2}}+{{r_{1}}^{2}}\right)}\ {r_{3}}}+{{r_{1}}\ {{r_{2}}^{2}}}-{{{r_{1}}^{2}}\ {r_{2}}}}}$ (18)

Type: Equation(Expression(Integer))
Example 4.1
fricas
```
eval(eq3_1,[r[2]=-r[1],r[3]=0])
```
$\label{eq19}{m_{X}}={{{x}^{3}}-{{{r_{1}}^{2}}\ x}}$ (19)

Type: Equation(Polynomial(Integer))

fricas
```
eq3_4:= eval(eval(eq3_2,[eq3_3a,eq3_3b,eq3_3c]),[r[2]=-r[1],r[3]=0])
```
$\label{eq20}{{e}^{X}}={{{{\left({{X}^{2}}+{{r_{1}}\ X}\right)}\ {{e}^{r_{1}}}}+{{\left({{X}^{2}}-{{r_{1}}\ X}\right)}\ {{e}^{-{r_{1}}}}}-{2 \ {{X}^{2}}}+{2 \ {{r_{1}}^{2}}}}\over{2 \ {{r_{1}}^{2}}}}$ (20)

Type: Equation(Expression(Integer))

fricas
```
htrigs rhs eq3_4
```
$\label{eq21}{{{r_{1}}\ X \ {\sinh \left({r_{1}}\right)}}+{{{X}^{2}}\ {\cosh \left({r_{1}}\right)}}-{{X}^{2}}+{{r_{1}}^{2}}}\over{{r_{1}}^{2}}$ (21)

Type: Expression(Integer)

Comment 4.2 (Rescaled enomorphism)
fricas
```
eq3_6:= X' = sinh(r[1])/r[1]*X
```
$\label{eq22}X' ={{X \ {\sinh \left({r_{1}}\right)}}\over{r_{1}}}$ (22)

Type: Equation(Expression(Integer))

fricas
```
eq3_7:= γ = cosh(r[1])
```
$\label{eq23}�� ={\cosh \left({r_{1}}\right)}$ (23)

Type: Equation(Expression(Integer))

fricas
```
eq3_8:= exp(X) = 1+X'+X'^2/(1+γ)
```
$\label{eq24}{{e}^{X}}={{{{\left(X' + 1 \right)}\ ��}+{{X'}^{2}}+ X' + 1}\over{�� + 1}}$ (24)

Type: Equation(Expression(Integer))

fricas
```
test(normalize(rhs eval(eq3_8,[eq3_6,eq3_7]) - rhs eq3_4)=0)
```
$\label{eq25} \mbox{\rm true}$ (25)

Type: Boolean

Exercise 4.3
fricas
```
eval(eq3_1,[r[3]=r[2]])
```
$\label{eq26}{m_{X}}={{{x}^{3}}+{{\left(-{2 \ {r_{2}}}-{r_{1}}\right)}\ {{x}^{2}}}+{{\left({{r_{2}}^{2}}+{2 \ {r_{1}}\ {r_{2}}}\right)}\ x}-{{r_{1}}\ {{r_{2}}^{2}}}}$ (26)

Type: Equation(Polynomial(Integer))

fricas
```
eq3_9a:=lhs eq3_3a = limit(rhs eq3_3a,r[3]=r[2])
```
$\label{eq27}{g_{0}}={{{{\left({{r_{1}}\ {{r_{2}}^{2}}}+{{\left(-{{r_{1}}^{2}}-{2 \ {r_{1}}}\right)}\ {r_{2}}}+{{r_{1}}^{2}}\right)}\ {{e}^{r_{2}}}}+{{{r_{2}}^{2}}\ {{e}^{r_{1}}}}}\over{{{r_{2}}^{2}}-{2 \ {r_{1}}\ {r_{2}}}+{{r_{1}}^{2}}}}$ (27)

Type: Equation(OrderedCompletion?(Expression(Integer)))

fricas
```
(numer rhs eq3_9a)/factor(denom rhs eq3_9a)
```
$\label{eq28}\begin{array}{@{}l} \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle {{1 \over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}\ {r_{1}}\ {{r_{2}}^{2}}}+ \ \ \displaystyle {{\left(-{{1 \over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}\ {{r_{1}}^{2}}}-{{2 \over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}\ {r_{1}}}\right)}\ {r_{2}}}+ \ \ \displaystyle {{1 \over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}\ {{r_{1}}^{2}}}$ (28)

Type: SparseMultivariatePolynomial?(Fraction(Factored(SparseMultivariatePolynomial?(Integer,Kernel(Expression(Integer))))),Kernel(Expression(Integer)))

fricas
```
eq3_9b:=lhs eq3_3b = limit(rhs eq3_3b,r[3]=r[2])
```
$\label{eq29}{g_{1}}={{{{\left(-{{r_{2}}^{2}}+{2 \ {r_{2}}}+{{r_{1}}^{2}}\right)}\ {{e}^{r_{2}}}}-{2 \ {r_{2}}\ {{e}^{r_{1}}}}}\over{{{r_{2}}^{2}}-{2 \ {r_{1}}\ {r_{2}}}+{{r_{1}}^{2}}}}$ (29)

Type: Equation(OrderedCompletion?(Expression(Integer)))

fricas
```
(numer rhs eq3_9b)/factor(denom rhs eq3_9b)
```
$\label{eq30}\begin{array}{@{}l} \displaystyle {{\left(-{{1 \over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}\ {{r_{2}}^{2}}}+{{2 \over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}\ {r_{2}}}+{{1 \over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}\ {{r_{1}}^{2}}}\right)}\ {{e}^{r_{2}}}}- \ \ \displaystyle {{2 \over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}\ {r_{2}}\ {{e}^{r_{1}}}}$ (30)

Type: SparseMultivariatePolynomial?(Fraction(Factored(SparseMultivariatePolynomial?(Integer,Kernel(Expression(Integer))))),Kernel(Expression(Integer)))

fricas
```
eq3_9c:=lhs eq3_3c = limit(rhs eq3_3c,r[3]=r[2])
```
$\label{eq31}{g_{2}}={{{{\left({r_{2}}-{r_{1}}- 1 \right)}\ {{e}^{r_{2}}}}+{{e}^{r_{1}}}}\over{{{r_{2}}^{2}}-{2 \ {r_{1}}\ {r_{2}}}+{{r_{1}}^{2}}}}$ (31)

Type: Equation(OrderedCompletion?(Expression(Integer)))

fricas
```
(numer rhs eq3_9c)/factor(denom rhs eq3_9c)
```
$\label{eq32}\begin{array}{@{}l} \displaystyle {{\left({{1 \over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}\ {r_{2}}}-{{1 \over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}\ {r_{1}}}-{1 \over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}\right)}\ {{e}^{r_{2}}}}+ \ \ \displaystyle {{1 \over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}\ {{e}^{r_{1}}}}$ (32)

Type: SparseMultivariatePolynomial?(Fraction(Factored(SparseMultivariatePolynomial?(Integer,Kernel(Expression(Integer))))),Kernel(Expression(Integer)))
Polynomial of degree 4
fricas
```
n:=4
```
$\label{eq33}4$ (33)

Type: PositiveInteger?

fricas
```
eq4_1:= m[X]=(x-r[1])*(x-r[2])*(x-r[3])*(x-r[4])
```
$\label{eq34}\begin{array}{@{}l} \displaystyle {m_{X}}={ \begin{array}{@{}l} \displaystyle {{x}^{4}}+{{\left(-{r_{4}}-{r_{3}}-{r_{2}}-{r_{1}}\right)}\ {{x}^{3}}}+ \ \ \displaystyle {{\left({{\left({r_{3}}+{r_{2}}+{r_{1}}\right)}\ {r_{4}}}+{{\left({r_{2}}+{r_{1}}\right)}\ {r_{3}}}+{{r_{1}}\ {r_{2}}}\right)}\ {{x}^{2}}}+ \ \ \displaystyle {{\left({{\left({{\left(-{r_{2}}-{r_{1}}\right)}\ {r_{3}}}-{{r_{1}}\ {r_{2}}}\right)}\ {r_{4}}}-{{r_{1}}\ {r_{2}}\ {r_{3}}}\right)}\ x}+ \ \ \displaystyle {{r_{1}}\ {r_{2}}\ {r_{3}}\ {r_{4}}}$ (34)

Type: Equation(Polynomial(Integer))

fricas
```
eq4_2:= g[0]=groupPolyCoeff(0)
```
$\label{eq35}\begin{array}{@{}l} \displaystyle {g_{0}}={{\left( \begin{array}{@{}l} \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle {{\left(-{{r_{1}}\ {{r_{2}}^{2}}}+{{{r_{1}}^{2}}\ {r_{2}}}\right)}\ {{r_{3}}^{3}}}+ \ \ \displaystyle {{\left({{r_{1}}\ {{r_{2}}^{3}}}-{{{r_{1}}^{3}}\ {r_{2}}}\right)}\ {{r_{3}}^{2}}}+ \ \ \displaystyle {{\left(-{{{r_{1}}^{2}}\ {{r_{2}}^{3}}}+{{{r_{1}}^{3}}\ {{r_{2}}^{2}}}\right)}\ {r_{3}}}$ (35)

Type: Equation(Expression(Integer))

fricas
```
eq4_3:= g[1]=groupPolyCoeff(1)
```
$\label{eq36}\begin{array}{@{}l} \displaystyle {g_{1}}={{\left( \begin{array}{@{}l} \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle {{\left({{r_{2}}^{2}}-{{r_{1}}^{2}}\right)}\ {{r_{3}}^{3}}}+ \ \ \displaystyle {{\left(-{{r_{2}}^{3}}+{{r_{1}}^{3}}\right)}\ {{r_{3}}^{2}}}+{{{r_{1}}^{2}}\ {{r_{2}}^{3}}}- \ \ \displaystyle {{{r_{1}}^{3}}\ {{r_{2}}^{2}}}$ (36)

Type: Equation(Expression(Integer))

fricas
```
eq4_4:= g[2]=groupPolyCoeff(2)
```
$\label{eq37}\begin{array}{@{}l} \displaystyle {g_{2}}={{\left( \begin{array}{@{}l} \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle {{\left(-{r_{2}}+{r_{1}}\right)}\ {{r_{3}}^{3}}}+{{\left({{r_{2}}^{3}}-{{r_{1}}^{3}}\right)}\ {r_{3}}}- \ \ \displaystyle {{r_{1}}\ {{r_{2}}^{3}}}+{{{r_{1}}^{3}}\ {r_{2}}}$ (37)

Type: Equation(Expression(Integer))

fricas
```
eq4_5:= g[3]=groupPolyCoeff(3)
```
$\label{eq38}\begin{array}{@{}l} \displaystyle {g_{3}}={{\left( \begin{array}{@{}l} \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle {{\left({r_{2}}-{r_{1}}\right)}\ {{r_{3}}^{2}}}+{{\left(-{{r_{2}}^{2}}+{{r_{1}}^{2}}\right)}\ {r_{3}}}+ \ \ \displaystyle {{r_{1}}\ {{r_{2}}^{2}}}-{{{r_{1}}^{2}}\ {r_{2}}}$ (38)

Type: Equation(Expression(Integer))
fricas
```
eq5_1:=eval(eq4_1,[r[3]=-r[1],r[4]=-r[2]])
```
$\label{eq39}{m_{X}}={{{x}^{4}}+{{\left(-{{r_{2}}^{2}}-{{r_{1}}^{2}}\right)}\ {{x}^{2}}}+{{{r_{1}}^{2}}\ {{r_{2}}^{2}}}}$ (39)

Type: Equation(Polynomial(Integer))
Corollary 6.1
fricas
```
eq5_2:= exp(X)=g[0]+g[1]*X+g[2]*X^2+g[3]*X^3
```
$\label{eq40}{{e}^{X}}={{{g_{3}}\ {{X}^{3}}}+{{g_{2}}\ {{X}^{2}}}+{{g_{1}}\ X}+{g_{0}}}$ (40)

Type: Equation(Expression(Integer))

fricas
```
eq5_3a:= eval(eq4_2,[r[3]=-r[1],r[4]=-r[2]])
```
$\label{eq41}{g_{0}}={{-{{{r_{1}}^{2}}\ {{e}^{r_{2}}}}+{{{r_{2}}^{2}}\ {{e}^{r_{1}}}}+{{{r_{2}}^{2}}\ {{e}^{-{r_{1}}}}}-{{{r_{1}}^{2}}\ {{e}^{-{r_{2}}}}}}\over{{2 \ {{r_{2}}^{2}}}-{2 \ {{r_{1}}^{2}}}}}$ (41)

Type: Equation(Expression(Integer))

fricas
```
htrigs rhs %
```
$\label{eq42}{-{{{r_{1}}^{2}}\ {\cosh \left({r_{2}}\right)}}+{{{r_{2}}^{2}}\ {\cosh \left({r_{1}}\right)}}}\over{{{r_{2}}^{2}}-{{r_{1}}^{2}}}$ (42)

Type: Expression(Integer)

fricas
```
eq5_3b:= eval(eq4_3,[r[3]=-r[1],r[4]=-r[2]])
```
$\label{eq43}{g_{1}}={{-{{{r_{1}}^{3}}\ {{e}^{r_{2}}}}+{{{r_{2}}^{3}}\ {{e}^{r_{1}}}}-{{{r_{2}}^{3}}\ {{e}^{-{r_{1}}}}}+{{{r_{1}}^{3}}\ {{e}^{-{r_{2}}}}}}\over{{2 \ {r_{1}}\ {{r_{2}}^{3}}}-{2 \ {{r_{1}}^{3}}\ {r_{2}}}}}$ (43)

Type: Equation(Expression(Integer))

fricas
```
htrigs rhs %
```
$\label{eq44}{-{{{r_{1}}^{3}}\ {\sinh \left({r_{2}}\right)}}+{{{r_{2}}^{3}}\ {\sinh \left({r_{1}}\right)}}}\over{{{r_{1}}\ {{r_{2}}^{3}}}-{{{r_{1}}^{3}}\ {r_{2}}}}$ (44)

Type: Expression(Integer)

fricas
```
eq5_3c:= eval(eq4_4,[r[3]=-r[1],r[4]=-r[2]])
```
$\label{eq45}{g_{2}}={{{{e}^{r_{2}}}-{{e}^{r_{1}}}-{{e}^{-{r_{1}}}}+{{e}^{-{r_{2}}}}}\over{{2 \ {{r_{2}}^{2}}}-{2 \ {{r_{1}}^{2}}}}}$ (45)

Type: Equation(Expression(Integer))

fricas
```
htrigs rhs %
```
$\label{eq46}{{\cosh \left({r_{2}}\right)}-{\cosh \left({r_{1}}\right)}}\over{{{r_{2}}^{2}}-{{r_{1}}^{2}}}$ (46)

Type: Expression(Integer)

fricas
```
eq5_3d:= eval(eq4_5,[r[3]=-r[1],r[4]=-r[2]])
```
$\label{eq47}{g_{3}}={{{{r_{1}}\ {{e}^{r_{2}}}}-{{r_{2}}\ {{e}^{r_{1}}}}+{{r_{2}}\ {{e}^{-{r_{1}}}}}-{{r_{1}}\ {{e}^{-{r_{2}}}}}}\over{{2 \ {r_{1}}\ {{r_{2}}^{3}}}-{2 \ {{r_{1}}^{3}}\ {r_{2}}}}}$ (47)

Type: Equation(Expression(Integer))

fricas
```
htrigs rhs %
```
$\label{eq48}{{{r_{1}}\ {\sinh \left({r_{2}}\right)}}-{{r_{2}}\ {\sinh \left({r_{1}}\right)}}}\over{{{r_{1}}\ {{r_{2}}^{3}}}-{{{r_{1}}^{3}}\ {r_{2}}}}$ (48)

Type: Expression(Integer)

fricas
```
eq5_4:= eval(eval(eq5_2,[eq4_2,eq4_3,eq4_4,eq4_5]),[r[3]=-r[1],r[4]=-r[2]])
```
$\label{eq49}\begin{array}{@{}l} \displaystyle {{e}^{X}}={{\left( \begin{array}{@{}l} \displaystyle {{\left({{r_{1}}\ {{X}^{3}}}+{{r_{1}}\ {r_{2}}\ {{X}^{2}}}-{{{r_{1}}^{3}}\ X}-{{{r_{1}}^{3}}\ {r_{2}}}\right)}\ {{e}^{r_{2}}}}+ \ \ \displaystyle {{\left(-{{r_{2}}\ {{X}^{3}}}-{{r_{1}}\ {r_{2}}\ {{X}^{2}}}+{{{r_{2}}^{3}}\ X}+{{r_{1}}\ {{r_{2}}^{3}}}\right)}\ {{e}^{r_{1}}}}+ \ \ \displaystyle {{\left({{r_{2}}\ {{X}^{3}}}-{{r_{1}}\ {r_{2}}\ {{X}^{2}}}-{{{r_{2}}^{3}}\ X}+{{r_{1}}\ {{r_{2}}^{3}}}\right)}\ {{e}^{-{r_{1}}}}}+ \ \ \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle -{{r_{1}}\ {{X}^{3}}}+{{r_{1}}\ {r_{2}}\ {{X}^{2}}}+{{{r_{1}}^{3}}\ X}- \ \ \displaystyle {{{r_{1}}^{3}}\ {r_{2}}}$ (49)

Type: Equation(Expression(Integer))

fricas
```
htrigs rhs %
```
$\label{eq50}{\left( \begin{array}{@{}l} \displaystyle {{\left({{r_{1}}\ {{X}^{3}}}-{{{r_{1}}^{3}}\ X}\right)}\ {\sinh \left({r_{2}}\right)}}+ \ \ \displaystyle {{\left(-{{r_{2}}\ {{X}^{3}}}+{{{r_{2}}^{3}}\ X}\right)}\ {\sinh \left({r_{1}}\right)}}+ \ \ \displaystyle {{\left({{r_{1}}\ {r_{2}}\ {{X}^{2}}}-{{{r_{1}}^{3}}\ {r_{2}}}\right)}\ {\cosh \left({r_{2}}\right)}}+ \ \ \displaystyle {{\left(-{{r_{1}}\ {r_{2}}\ {{X}^{2}}}+{{r_{1}}\ {{r_{2}}^{3}}}\right)}\ {\cosh \left({r_{1}}\right)}}$ (50)

Type: Expression(Integer)

Definition 6.2
fricas
```
eq5_5a:= Y[1] = 1/(2*r[1]^2-r[1]^2-r[2]^2)*(X^3-(r[1]^2+r[2]^2-r[1]^2)*X)
```
$\label{eq51}{Y_{1}}={{-{{X}^{3}}+{{{r_{2}}^{2}}\ X}}\over{{{r_{2}}^{2}}-{{r_{1}}^{2}}}}$ (51)

Type: Equation(Fraction(Polynomial(Integer)))

fricas
```
eq5_5b:= Y[2] = 1/(2*r[2]^2-r[1]^2-r[2]^2)*(X^3-(r[1]^2+r[2]^2-r[2]^2)*X)
```
$\label{eq52}{Y_{2}}={{{{X}^{3}}-{{{r_{1}}^{2}}\ X}}\over{{{r_{2}}^{2}}-{{r_{1}}^{2}}}}$ (52)

Type: Equation(Fraction(Polynomial(Integer)))

Exercise 6.3
fricas
```
eq5_6a:= X = Y[1]+Y[2]
```
$\label{eq53}X ={{Y_{2}}+{Y_{1}}}$ (53)

Type: Equation(Polynomial(Integer))

fricas
```
test(eval(eq5_6a,[eq5_5a,eq5_5b]))
```
$\label{eq54} \mbox{\rm true}$ (54)

Type: Boolean

fricas
```
eq5_6b:= eval(Y[1]*Y[2]=0,[eq5_5a,eq5_5b])
```
$\label{eq55}{{-{{X}^{6}}+{{\left({{r_{2}}^{2}}+{{r_{1}}^{2}}\right)}\ {{X}^{4}}}-{{{r_{1}}^{2}}\ {{r_{2}}^{2}}\ {{X}^{2}}}}\over{{{r_{2}}^{4}}-{2 \ {{r_{1}}^{2}}\ {{r_{2}}^{2}}}+{{r_{1}}^{4}}}}= 0$ (55)

Type: Equation(Expression(Integer))

fricas
```
eq5_6c:= X^4 = X^4-eval(rhs eq5_1,x=X)
```
$\label{eq56}{{X}^{4}}={{{\left({{r_{2}}^{2}}+{{r_{1}}^{2}}\right)}\ {{X}^{2}}}-{{{r_{1}}^{2}}\ {{r_{2}}^{2}}}}$ (56)

Type: Equation(Polynomial(Integer))

fricas
```
eq5_6d:= X^2*(lhs %)=X^2*(rhs %)
```
$\label{eq57}{{X}^{6}}={{{\left({{r_{2}}^{2}}+{{r_{1}}^{2}}\right)}\ {{X}^{4}}}-{{{r_{1}}^{2}}\ {{r_{2}}^{2}}\ {{X}^{2}}}}$ (57)

Type: Equation(Polynomial(Integer))

fricas
```
test(_rule(lhs eq5_6d,rhs eq5_6d)(lhs eq5_6b)=rhs eq5_6b)
```
$\label{eq58} \mbox{\rm true}$ (58)

Type: Boolean

Comment 6.5 (Rescaling)
fricas
```
eq5_7:= sinh(r[1])/r[1]*Y[1]+sinh(r[2])/r[2]*Y[2]
```
$\label{eq59}{{{Y_{2}}\ {r_{1}}\ {\sinh \left({r_{2}}\right)}}+{{Y_{1}}\ {r_{2}}\ {\sinh \left({r_{1}}\right)}}}\over{{r_{1}}\ {r_{2}}}$ (59)

Type: Expression(Integer)

fricas
```
eq5_8a:= [ Y'[1]=sinh(r[1])/r[1]*Y[1], Y'[2]=sinh(r[2])/r[2]*Y[2] ]
```
$\label{eq60}\left[{{Y'_{1}}={{{Y_{1}}\ {\sinh \left({r_{1}}\right)}}\over{r_{1}}}}, \:{{Y'_{2}}={{{Y_{2}}\ {\sinh \left({r_{2}}\right)}}\over{r_{2}}}}\right]$ (60)

Type: List(Equation(Expression(Integer)))

fricas
```
eq5_8b:= [ γ[1] = cosh(r[1]), γ[2] = cosh(r[2]) ]
```
$\label{eq61}\left[{{��_{1}}={\cosh \left({r_{1}}\right)}}, \:{{��_{2}}={\cosh \left({r_{2}}\right)}}\right]$ (61)

Type: List(Equation(Expression(Integer)))

fricas
```
eq5_9a:= exp(X) = exp(Y[1])*exp(Y[2])
```
$\label{eq62}{{e}^{X}}={{{e}^{Y_{1}}}\ {{e}^{Y_{2}}}}$ (62)

Type: Equation(Expression(Integer))

fricas
```
eval(eq5_9a,[eq5_5a,eq5_5b])
```
$\label{eq63}{{e}^{X}}={{{e}^{{-{{X}^{3}}+{{{r_{2}}^{2}}\ X}}\over{{{r_{2}}^{2}}-{{r_{1}}^{2}}}}}\ {{e}^{{{{X}^{3}}-{{{r_{1}}^{2}}\ X}}\over{{{r_{2}}^{2}}-{{r_{1}}^{2}}}}}}$ (63)

Type: Equation(Expression(Integer))

fricas
```
test(lhs % = simplify expand rhs %)
```
$\label{eq64} \mbox{\rm true}$ (64)

Type: Boolean

fricas
```
eq5_9b:= exp(X) = 1 + Y'[1] +Y'[2] + Y'[1]^2/(1+γ[1]) + Y'[2]^2/(1+γ[2])
```
$\label{eq65}\begin{array}{@{}l} \displaystyle {{e}^{X}}={{\left( \begin{array}{@{}l} \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle {{\left({Y'_{2}}+{Y'_{1}}+ 1 \right)}\ {��_{1}}}+{Y'_{2}}+{{Y'_{1}}^{2}}+ \ \ \displaystyle {Y'_{1}}+ 1$ (65)

Type: Equation(Expression(Integer))

fricas
```
normalize eval(eval(rhs eq5_9b,concat [eq5_8a,eq5_8b]),[eq5_5a,eq5_5b])
```
$\label{eq66}{\left( \begin{array}{@{}l} \displaystyle { \begin{array}{@{}l} \displaystyle {\left({ \begin{array}{@{}l} \displaystyle {{{r_{1}}^{2}}\ {{X}^{6}}}-{2 \ {{r_{1}}^{4}}\ {{X}^{4}}}+{{\left({{{r_{1}}^{2}}\ {{r_{2}}^{3}}}-{{{r_{1}}^{4}}\ {r_{2}}}\right)}\ {{X}^{3}}}+ \ \ \displaystyle {{{r_{1}}^{6}}\ {{X}^{2}}}+{{\left(-{{{r_{1}}^{4}}\ {{r_{2}}^{3}}}+{{{r_{1}}^{6}}\ {r_{2}}}\right)}\ X}$ (66)

Type: Expression(Integer)

fricas
```
_rule(lhs eq5_6d,rhs eq5_6d)(%)
```
$\label{eq67}{\left( \begin{array}{@{}l} \displaystyle {{\left({{{r_{1}}^{2}}\ {{X}^{4}}}+{{{r_{1}}^{2}}\ {r_{2}}\ {{X}^{3}}}-{{{r_{1}}^{4}}\ {{X}^{2}}}-{{{r_{1}}^{4}}\ {r_{2}}\ X}\right)}\ {{e}^{r_{1}}}\ {{{e}^{r_{2}}}^{2}}}+ \ \ \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle -{{{r_{2}}^{2}}\ {{X}^{4}}}-{{r_{1}}\ {{r_{2}}^{2}}\ {{X}^{3}}}+ \ \ \displaystyle {{{r_{2}}^{4}}\ {{X}^{2}}}+{{r_{1}}\ {{r_{2}}^{4}}\ X}$ (67)

Type: Expression(Integer)

fricas
```
_rule(lhs eq5_6c,rhs eq5_6c)(%)
```
$\label{eq68}{\left( \begin{array}{@{}l} \displaystyle {{\left({{r_{1}}\ {{X}^{3}}}+{{r_{1}}\ {r_{2}}\ {{X}^{2}}}-{{{r_{1}}^{3}}\ X}-{{{r_{1}}^{3}}\ {r_{2}}}\right)}\ {{e}^{r_{1}}}\ {{{e}^{r_{2}}}^{2}}}+ \ \ \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle -{{r_{2}}\ {{X}^{3}}}-{{r_{1}}\ {r_{2}}\ {{X}^{2}}}+ \ \ \displaystyle {{{r_{2}}^{3}}\ X}+{{r_{1}}\ {{r_{2}}^{3}}}$ (68)

Type: Expression(Integer)

fricas
```
test(normalize(% - rhs eq5_4) = 0)
```
$\label{eq69} \mbox{\rm true}$ (69)

Type: Boolean

Multiple roots for polynomial of degree four

Exercise 7.1

fricas

eval(eq4_1,r[4]=r[3])

$\label{eq70}\begin{array}{@{}l} \displaystyle {m_{X}}={ \begin{array}{@{}l} \displaystyle {{x}^{4}}+{{\left(-{2 \ {r_{3}}}-{r_{2}}-{r_{1}}\right)}\ {{x}^{3}}}+ \ \ \displaystyle {{\left({{r_{3}}^{2}}+{{\left({2 \ {r_{2}}}+{2 \ {r_{1}}}\right)}\ {r_{3}}}+{{r_{1}}\ {r_{2}}}\right)}\ {{x}^{2}}}+ \ \ \displaystyle {{\left({{\left(-{r_{2}}-{r_{1}}\right)}\ {{r_{3}}^{2}}}-{2 \ {r_{1}}\ {r_{2}}\ {r_{3}}}\right)}\ x}+{{r_{1}}\ {r_{2}}\ {{r_{3}}^{2}}}$

(70)

Type: Equation(Polynomial(Integer))

fricas

eq6_1a:=lhs eq4_2 = limit(rhs eq4_2,r[4]=r[3])

$\label{eq71}\begin{array}{@{}l} \displaystyle {g_{0}}={{\left( \begin{array}{@{}l} \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle {{\left(-{{r_{1}}\ {{r_{2}}^{2}}}+{{{r_{1}}^{2}}\ {r_{2}}}\right)}\ {{r_{3}}^{3}}}+ \ \ \displaystyle {{\left({{{r_{1}}\ {{r_{2}}^{3}}}+{3 \ {r_{1}}\ {{r_{2}}^{2}}}+{{\left(-{{r_{1}}^{3}}-{3 \ {{r_{1}}^{2}}}\right)}\ {r_{2}}}}\right)}\ {{r_{3}}^{2}}}+ \ \ \displaystyle {{\left({{{\left(-{{r_{1}}^{2}}-{2 \ {r_{1}}}\right)}\ {{r_{2}}^{3}}}+{{{r_{1}}^{3}}\ {{r_{2}}^{2}}}+{2 \ {{r_{1}}^{3}}\ {r_{2}}}}\right)}\ {r_{3}}}+ \ \ \displaystyle {{{r_{1}}^{2}}\ {{r_{2}}^{3}}}-{{{r_{1}}^{3}}\ {{r_{2}}^{2}}}$

(71)

Type: Equation(OrderedCompletion?(Expression(Integer)))

fricas

collect(rhs(eq6_1a), exp(r[1]))::OutputForm+collect(rhs(eq6_1a), exp(r[2]))::OutputForm+ _
  sum _
    [((factor numer x)/(factor denom x))::OutputForm _
       for x in collector(collect(rhs(eq6_1a), exp(r[3])),(r[3]-r[1])::Expression Integer)]

fricas

Compiling function collect with type (OrderedCompletion(Expression(
      Integer)), Expression(Integer)) -> Fraction(Factored(
      SparseMultivariatePolynomial(Integer,Kernel(Expression(Integer)))
      ))

fricas

Compiling function sum with type List(OutputForm) -> OutputForm

$\label{eq72}\begin{array}{@{}l} \displaystyle {{{r_{2}}\ {{r_{3}}^{2}}\ {{e}^{r_{1}}}}\over{{\left({r_{2}}-{r_{1}}\right)}\ {{\left({r_{3}}-{r_{1}}\right)}^{2}}}}-{{{r_{1}}\ {{r_{3}}^{2}}\ {{e}^{r_{2}}}}\over{{\left({r_{2}}-{r_{1}}\right)}\ {{\left({r_{3}}-{r_{2}}\right)}^{2}}}}+ \ \ \displaystyle {{{r_{2}}\ {\left({{r_{3}}^{2}}+{{\left(-{r_{2}}- 2 \right)}\ {r_{3}}}+{r_{2}}\right)}\ {{e}^{r_{3}}}}\over{{\left({r_{3}}-{r_{2}}\right)}^{2}}}- \ \ \displaystyle {{{r_{2}}\ {\left({r_{3}}-{r_{2}}- 1 \right)}\ {{r_{3}}^{2}}\ {{e}^{r_{3}}}}\over{{{\left({r_{3}}-{r_{2}}\right)}^{2}}\ {\left({r_{3}}-{r_{1}}\right)}}}+{{{r_{2}}\ {{r_{3}}^{2}}\ {{e}^{r_{3}}}}\over{{\left({r_{3}}-{r_{2}}\right)}\ {{\left({r_{3}}-{r_{1}}\right)}^{2}}}}$

(72)

Type: OutputForm?

fricas

eq6_1b:=lhs eq4_3 = limit(rhs eq4_3,r[4]=r[3])

$\label{eq73}\begin{array}{@{}l} \displaystyle {g_{1}}={{\left( \begin{array}{@{}l} \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle {{\left({{r_{2}}^{2}}-{{r_{1}}^{2}}\right)}\ {{r_{3}}^{3}}}+ \ \ \displaystyle {{\left(-{{r_{2}}^{3}}-{3 \ {{r_{2}}^{2}}}+{{r_{1}}^{3}}+{3 \ {{r_{1}}^{2}}}\right)}\ {{r_{3}}^{2}}}+ \ \ \displaystyle {{\left({2 \ {{r_{2}}^{3}}}-{2 \ {{r_{1}}^{3}}}\right)}\ {r_{3}}}+{{{r_{1}}^{2}}\ {{r_{2}}^{3}}}- \ \ \displaystyle {{{r_{1}}^{3}}\ {{r_{2}}^{2}}}$

(73)

Type: Equation(OrderedCompletion?(Expression(Integer)))

fricas

collect(rhs(eq6_1b), exp(r[1]))::OutputForm+collect(rhs(eq6_1b), exp(r[2]))::OutputForm+ _
  sum _
    [((factor numer x)/(factor denom x))::OutputForm _
       for x in collector(collect(rhs(eq6_1b), exp(r[3])),(r[3]-r[1])::Expression Integer)]

$\label{eq74}\begin{array}{@{}l} \displaystyle -{{{r_{3}}\ {\left({r_{3}}+{2 \ {r_{2}}}\right)}\ {{e}^{r_{1}}}}\over{{\left({r_{2}}-{r_{1}}\right)}\ {{\left({r_{3}}-{r_{1}}\right)}^{2}}}}+{{{r_{3}}\ {\left({r_{3}}+{2 \ {r_{1}}}\right)}\ {{e}^{r_{2}}}}\over{{\left({r_{2}}-{r_{1}}\right)}\ {{\left({r_{3}}-{r_{2}}\right)}^{2}}}}- \ \ \displaystyle {{{\left({{r_{3}}^{2}}-{2 \ {r_{3}}}-{{r_{2}}^{2}}\right)}\ {{e}^{r_{3}}}}\over{{\left({r_{3}}-{r_{2}}\right)}^{2}}}+{{{\left({r_{3}}-{r_{2}}- 1 \right)}\ {r_{3}}\ {\left({r_{3}}+{2 \ {r_{2}}}\right)}\ {{e}^{r_{3}}}}\over{{{\left({r_{3}}-{r_{2}}\right)}^{2}}\ {\left({r_{3}}-{r_{1}}\right)}}}- \ \ \displaystyle {{{r_{3}}\ {\left({r_{3}}+{2 \ {r_{2}}}\right)}\ {{e}^{r_{3}}}}\over{{\left({r_{3}}-{r_{2}}\right)}\ {{\left({r_{3}}-{r_{1}}\right)}^{2}}}}$

(74)

Type: OutputForm?

fricas

eq6_1c:=lhs eq4_4 = limit(rhs eq4_4,r[4]=r[3])

$\label{eq75}\begin{array}{@{}l} \displaystyle {g_{2}}={{\left( \begin{array}{@{}l} \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle {{\left(-{r_{2}}+{r_{1}}\right)}\ {{r_{3}}^{3}}}+{{\left({3 \ {r_{2}}}-{3 \ {r_{1}}}\right)}\ {{r_{3}}^{2}}}+ \ \ \displaystyle {{\left({{r_{2}}^{3}}-{{r_{1}}^{3}}\right)}\ {r_{3}}}+{{\left(-{r_{1}}- 1 \right)}\ {{r_{2}}^{3}}}+ \ \ \displaystyle {{{r_{1}}^{3}}\ {r_{2}}}+{{r_{1}}^{3}}$

(75)

Type: Equation(OrderedCompletion?(Expression(Integer)))

fricas

collect(rhs(eq6_1c), exp(r[1]))::OutputForm+collect(rhs(eq6_1c), exp(r[2]))::OutputForm+ _
  sum _
    [((factor numer x)/(factor denom x))::OutputForm _
       for x in collector(collect(rhs(eq6_1c), exp(r[3])),(r[3]-r[1])::Expression Integer)]

$\label{eq76}\begin{array}{@{}l} \displaystyle {{{\left({2 \ {r_{3}}}+{r_{2}}\right)}\ {{e}^{r_{1}}}}\over{{\left({r_{2}}-{r_{1}}\right)}\ {{\left({r_{3}}-{r_{1}}\right)}^{2}}}}-{{{\left({2 \ {r_{3}}}+{r_{1}}\right)}\ {{e}^{r_{2}}}}\over{{\left({r_{2}}-{r_{1}}\right)}\ {{\left({r_{3}}-{r_{2}}\right)}^{2}}}}+ \ \ \displaystyle {{{\left({r_{3}}-{r_{2}}- 1 \right)}\ {{e}^{r_{3}}}}\over{{\left({r_{3}}-{r_{2}}\right)}^{2}}}-{{{\left({r_{3}}-{r_{2}}- 1 \right)}\ {\left({2 \ {r_{3}}}+{r_{2}}\right)}\ {{e}^{r_{3}}}}\over{{{\left({r_{3}}-{r_{2}}\right)}^{2}}\ {\left({r_{3}}-{r_{1}}\right)}}}+ \ \ \displaystyle {{{\left({2 \ {r_{3}}}+{r_{2}}\right)}\ {{e}^{r_{3}}}}\over{{\left({r_{3}}-{r_{2}}\right)}\ {{\left({r_{3}}-{r_{1}}\right)}^{2}}}}$

(76)

Type: OutputForm?

fricas

eq6_1d:=lhs eq4_5 = limit(rhs eq4_5,r[4]=r[3])

$\label{eq77}\begin{array}{@{}l} \displaystyle {g_{3}}={{\left( \begin{array}{@{}l} \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle {{\left({r_{2}}-{r_{1}}\right)}\ {{r_{3}}^{2}}}+ \ \ \displaystyle {{\left(-{{r_{2}}^{2}}-{2 \ {r_{2}}}+{{r_{1}}^{2}}+{2 \ {r_{1}}}\right)}\ {r_{3}}}+ \ \ \displaystyle {{\left({r_{1}}+ 1 \right)}\ {{r_{2}}^{2}}}-{{{r_{1}}^{2}}\ {r_{2}}}-{{r_{1}}^{2}}$

(77)

Type: Equation(OrderedCompletion?(Expression(Integer)))

fricas

collect(rhs(eq6_1d), exp(r[1]))::OutputForm+collect(rhs(eq6_1d), exp(r[2]))::OutputForm+ _
  sum _
    [((factor numer x)/(factor denom x))::OutputForm _
       for x in collector(collect(rhs(eq6_1d), exp(r[3])),(r[3]-r[1])::Expression Integer)]

$\label{eq78}\begin{array}{@{}l} \displaystyle -{{{e}^{r_{1}}}\over{{\left({r_{2}}-{r_{1}}\right)}\ {{\left({r_{3}}-{r_{1}}\right)}^{2}}}}+{{{e}^{r_{2}}}\over{{\left({r_{2}}-{r_{1}}\right)}\ {{\left({r_{3}}-{r_{2}}\right)}^{2}}}}+ \ \ \displaystyle {{{\left({r_{3}}-{r_{2}}- 1 \right)}\ {{e}^{r_{3}}}}\over{{{\left({r_{3}}-{r_{2}}\right)}^{2}}\ {\left({r_{3}}-{r_{1}}\right)}}}-{{{e}^{r_{3}}}\over{{\left({r_{3}}-{r_{2}}\right)}\ {{\left({r_{3}}-{r_{1}}\right)}^{2}}}}$

(78)

Type: OutputForm?

Exercise 7.3 (Double root)

fricas

eval(eq4_1,[r[3]=r[1],r[4]=r[2]])

$\label{eq79}\begin{array}{@{}l} \displaystyle {m_{X}}={ \begin{array}{@{}l} \displaystyle {{x}^{4}}+{{\left(-{2 \ {r_{2}}}-{2 \ {r_{1}}}\right)}\ {{x}^{3}}}+{{\left({{r_{2}}^{2}}+{4 \ {r_{1}}\ {r_{2}}}+{{r_{1}}^{2}}\right)}\ {{x}^{2}}}+ \ \ \displaystyle {{\left(-{2 \ {r_{1}}\ {{r_{2}}^{2}}}-{2 \ {{r_{1}}^{2}}\ {r_{2}}}\right)}\ x}+{{{r_{1}}^{2}}\ {{r_{2}}^{2}}}$

(79)

Type: Equation(Polynomial(Integer))

fricas

eq6_3a:=lhs eq4_2 = limit(limit(rhs eq4_2,r[3]=r[1]),r[4]=r[2])

$\label{eq80}\begin{array}{@{}l} \displaystyle {g_{0}}={{\left( \begin{array}{@{}l} \displaystyle {{\left(-{{{r_{1}}^{2}}\ {{r_{2}}^{2}}}+{{\left({{r_{1}}^{3}}+{3 \ {{r_{1}}^{2}}}\right)}\ {r_{2}}}-{{r_{1}}^{3}}\right)}\ {{e}^{r_{2}}}}+ \ \ \displaystyle {{\left({{\left(-{r_{1}}+ 1 \right)}\ {{r_{2}}^{3}}}+{{\left({{r_{1}}^{2}}-{3 \ {r_{1}}}\right)}\ {{r_{2}}^{2}}}\right)}\ {{e}^{r_{1}}}}$

(80)

Type: Equation(OrderedCompletion?(Expression(Integer)))

fricas

sum concat( _
  [((factor numer x)/(factor denom x))::OutputForm _
     for x in collector(collect(rhs(eq6_3a), exp(r[1])),(r[2]-r[1])::Expression Integer)] , _
  [((factor numer x)/(factor denom x))::OutputForm _
     for x in collector(collect(rhs(eq6_3a), exp(r[2])),(r[2]-r[1])::Expression Integer)] )

$\label{eq81}\begin{array}{@{}l} \displaystyle {{{{r_{2}}^{2}}\ {{e}^{r_{1}}}}\over{{r_{2}}-{r_{1}}}}-{{{\left({r_{2}}- 3 \right)}\ {{r_{2}}^{2}}\ {{e}^{r_{1}}}}\over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}-{{2 \ {{r_{2}}^{3}}\ {{e}^{r_{1}}}}\over{{\left({r_{2}}-{r_{1}}\right)}^{3}}}-{{\left({r_{2}}- 1 \right)}\ {{e}^{r_{2}}}}+ \ \ \displaystyle {{2 \ {{r_{2}}^{2}}\ {{e}^{r_{2}}}}\over{{r_{2}}-{r_{1}}}}-{{{{r_{2}}^{2}}\ {\left({r_{2}}+ 3 \right)}\ {{e}^{r_{2}}}}\over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}+{{2 \ {{r_{2}}^{3}}\ {{e}^{r_{2}}}}\over{{\left({r_{2}}-{r_{1}}\right)}^{3}}}$

(81)

Type: OutputForm?

fricas

eq6_3b:=lhs eq4_3 = limit(limit(rhs eq4_3,r[3]=r[1]),r[4]=r[2])

$\label{eq82}\begin{array}{@{}l} \displaystyle {g_{1}}={{\left( \begin{array}{@{}l} \displaystyle {{\left({2 \ {r_{1}}\ {{r_{2}}^{2}}}+{{\left(-{{r_{1}}^{2}}-{6 \ {r_{1}}}\right)}\ {r_{2}}}-{{r_{1}}^{3}}\right)}\ {{e}^{r_{2}}}}+ \ \ \displaystyle {{\left({{r_{2}}^{3}}+{{r_{1}}\ {{r_{2}}^{2}}}+{{\left(-{2 \ {{r_{1}}^{2}}}+{6 \ {r_{1}}}\right)}\ {r_{2}}}\right)}\ {{e}^{r_{1}}}}$

(82)

Type: Equation(OrderedCompletion?(Expression(Integer)))

fricas

sum concat( _
  [((factor numer x)/(factor denom x))::OutputForm _
     for x in collector(collect(rhs(eq6_3b), exp(r[1])),(r[2]-r[1])::Expression Integer)] , _
  [((factor numer x)/(factor denom x))::OutputForm _
     for x in collector(collect(rhs(eq6_3b), exp(r[2])),(r[2]-r[1])::Expression Integer)] )

$\label{eq83}\begin{array}{@{}l} \displaystyle -{{2 \ {r_{2}}\ {{e}^{r_{1}}}}\over{{r_{2}}-{r_{1}}}}+{{3 \ {\left({r_{2}}- 2 \right)}\ {r_{2}}\ {{e}^{r_{1}}}}\over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}+{{6 \ {{r_{2}}^{2}}\ {{e}^{r_{1}}}}\over{{\left({r_{2}}-{r_{1}}\right)}^{3}}}+{{e}^{r_{2}}}- \ \ \displaystyle {{4 \ {r_{2}}\ {{e}^{r_{2}}}}\over{{r_{2}}-{r_{1}}}}+{{3 \ {r_{2}}\ {\left({r_{2}}+ 2 \right)}\ {{e}^{r_{2}}}}\over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}-{{6 \ {{r_{2}}^{2}}\ {{e}^{r_{2}}}}\over{{\left({r_{2}}-{r_{1}}\right)}^{3}}}$

(83)

Type: OutputForm?

fricas

eq6_3c:=lhs eq4_4 = limit(limit(rhs eq4_4,r[3]=r[1]),r[4]=r[2])

$\label{eq84}\begin{array}{@{}l} \displaystyle {g_{2}}={{\left( \begin{array}{@{}l} \displaystyle {{\left(-{{r_{2}}^{2}}+{{\left(-{r_{1}}+ 3 \right)}\ {r_{2}}}+{2 \ {{r_{1}}^{2}}}+{3 \ {r_{1}}}\right)}\ {{e}^{r_{2}}}}+ \ \ \displaystyle {{\left(-{2 \ {{r_{2}}^{2}}}+{{\left({r_{1}}- 3 \right)}\ {r_{2}}}+{{r_{1}}^{2}}-{3 \ {r_{1}}}\right)}\ {{e}^{r_{1}}}}$

(84)

Type: Equation(OrderedCompletion?(Expression(Integer)))

fricas

sum concat( _
  [((factor numer x)/(factor denom x))::OutputForm _
     for x in collector(collect(rhs(eq6_3c), exp(r[1])),(r[2]-r[1])::Expression Integer)] , _
  [((factor numer x)/(factor denom x))::OutputForm _
     for x in collector(collect(rhs(eq6_3c), exp(r[2])),(r[2]-r[1])::Expression Integer)] )

$\label{eq85}\begin{array}{@{}l} \displaystyle {{{e}^{r_{1}}}\over{{r_{2}}-{r_{1}}}}-{{3 \ {\left({r_{2}}- 1 \right)}\ {{e}^{r_{1}}}}\over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}-{{6 \ {r_{2}}\ {{e}^{r_{1}}}}\over{{\left({r_{2}}-{r_{1}}\right)}^{3}}}+{{2 \ {{e}^{r_{2}}}}\over{{r_{2}}-{r_{1}}}}- \ \ \displaystyle {{3 \ {\left({r_{2}}+ 1 \right)}\ {{e}^{r_{2}}}}\over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}+{{6 \ {r_{2}}\ {{e}^{r_{2}}}}\over{{\left({r_{2}}-{r_{1}}\right)}^{3}}}$

(85)

Type: OutputForm?

fricas

eq6_3d:=lhs eq4_5 = limit(limit(rhs eq4_5,r[3]=r[1]),r[4]=r[2])

$\label{eq86}{g_{3}}={{{{\left({r_{2}}-{r_{1}}- 2 \right)}\ {{e}^{r_{2}}}}+{{\left({r_{2}}-{r_{1}}+ 2 \right)}\ {{e}^{r_{1}}}}}\over{{{r_{2}}^{3}}-{3 \ {r_{1}}\ {{r_{2}}^{2}}}+{3 \ {{r_{1}}^{2}}\ {r_{2}}}-{{r_{1}}^{3}}}}$

(86)

Type: Equation(OrderedCompletion?(Expression(Integer)))

fricas

sum concat( _
  [((factor numer x)/(factor denom x))::OutputForm _
     for x in collector(collect(rhs(eq6_3d), exp(r[1])),(r[2]-r[1])::Expression Integer)] , _
  [((factor numer x)/(factor denom x))::OutputForm _
     for x in collector(collect(rhs(eq6_3d), exp(r[2])),(r[2]-r[1])::Expression Integer)] )

$\label{eq87}{{{e}^{r_{1}}}\over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}+{{2 \ {{e}^{r_{1}}}}\over{{\left({r_{2}}-{r_{1}}\right)}^{3}}}+{{{e}^{r_{2}}}\over{{\left({r_{2}}-{r_{1}}\right)}^{2}}}-{{2 \ {{e}^{r_{2}}}}\over{{\left({r_{2}}-{r_{1}}\right)}^{3}}}$

(87)

Type: OutputForm?

Exercise 7.4 (Triple root)

fricas

eval(eq4_1,[r[3]=r[2],r[4]=r[2]])

$\label{eq88}\begin{array}{@{}l} \displaystyle {m_{X}}={ \begin{array}{@{}l} \displaystyle {{x}^{4}}+{{\left(-{3 \ {r_{2}}}-{r_{1}}\right)}\ {{x}^{3}}}+{{\left({3 \ {{r_{2}}^{2}}}+{3 \ {r_{1}}\ {r_{2}}}\right)}\ {{x}^{2}}}+ \ \ \displaystyle {{\left(-{{r_{2}}^{3}}-{3 \ {r_{1}}\ {{r_{2}}^{2}}}\right)}\ x}+{{r_{1}}\ {{r_{2}}^{3}}}$

(88)

Type: Equation(Polynomial(Integer))

fricas

eq6_4a:=lhs eq4_2 = limit(limit(rhs eq4_2,r[3]=r[2]),r[4]=r[2])

$\label{eq89}\begin{array}{@{}l} \displaystyle {g_{0}}={{\left( \begin{array}{@{}l} \displaystyle {{\left({ \begin{array}{@{}l} \displaystyle -{{r_{1}}\ {{r_{2}}^{4}}}+{{\left({2 \ {{r_{1}}^{2}}}+{4 \ {r_{1}}}\right)}\ {{r_{2}}^{3}}}+ \ \ \displaystyle {{\left(-{{r_{1}}^{3}}-{6 \ {{r_{1}}^{2}}}-{6 \ {r_{1}}}\right)}\ {{r_{2}}^{2}}}+ \ \ \displaystyle {{\left({2 \ {{r_{1}}^{3}}}+{6 \ {{r_{1}}^{2}}}\right)}\ {r_{2}}}-{2 \ {{r_{1}}^{3}}}$

(89)

Type: Equation(OrderedCompletion?(Expression(Integer)))

fricas

sum concat(collect(rhs(eq6_4a), exp(r[1]))::OutputForm, _
  [((factor numer x)/(factor denom x))::OutputForm _
     for x in collector(collect(rhs(eq6_4a), exp(r[2])),(r[2]-r[1])::Expression Integer)] )

   >> Error detected within library code:
   "failed" of mode Union(SparseMultivariatePolynomial(Integer,Kernel(Expression(Integer))),"failed") cannot be coerced to mode SparseMultivariatePolynomial(Integer,Kernel(Expression(Integer)))

Parabolic isometries: single many-fold root
Exercise 8.1 (Degree two)
fricas
```
eval(eq2_2,[r[2]=r[1]])
```
$\label{eq90}{{e}^{X}}={{{g_{1}}\ X}+{g_{0}}}$ (90)

Type: Equation(Expression(Integer))

fricas
```
lhs eq2_3a = limit(rhs eq2_3a,r[2]=r[1])
```
$\label{eq91}{g_{0}}={{\left(-{r_{1}}+ 1 \right)}\ {{e}^{r_{1}}}}$ (91)

Type: Equation(OrderedCompletion?(Expression(Integer)))

fricas
```
lhs eq2_3b = limit(rhs eq2_3b,r[2]=r[1])
```
$\label{eq92}{g_{1}}={{e}^{r_{1}}}$ (92)

Type: Equation(OrderedCompletion?(Expression(Integer)))

Exercise 8.2 (Triple root)
fricas
```
eval(eq3_1,[r[2]=r[1],r[3]=r[1]])
```
$\label{eq93}{m_{X}}={{{x}^{3}}-{3 \ {r_{1}}\ {{x}^{2}}}+{3 \ {{r_{1}}^{2}}\ x}-{{r_{1}}^{3}}}$ (93)

Type: Equation(Polynomial(Integer))

fricas
```
lhs eq3_3a = limit(limit(rhs eq3_3a,r[2]=r[1]),r[3]=r[1])
```
$\label{eq94}{g_{0}}={{{\left({{r_{1}}^{2}}-{2 \ {r_{1}}}+ 2 \right)}\ {{e}^{r_{1}}}}\over 2}$ (94)

Type: Equation(OrderedCompletion?(Expression(Integer)))

fricas
```
lhs eq3_3b = limit(limit(rhs eq3_3b,r[2]=r[1]),r[3]=r[1])
```
$\label{eq95}{g_{1}}={{\left(-{r_{1}}+ 1 \right)}\ {{e}^{r_{1}}}}$ (95)

Type: Equation(OrderedCompletion?(Expression(Integer)))

fricas
```
lhs eq3_3c = limit(limit(rhs eq3_3c,r[2]=r[1]),r[3]=r[1])
```
$\label{eq96}{g_{2}}={{{e}^{r_{1}}}\over 2}$ (96)

Type: Equation(OrderedCompletion?(Expression(Integer)))

Exercise 8.3 (Fourfold root)
fricas
```
eval(eq4_1,[r[2]=r[1],r[3]=r[1],r[4]=r[1]])
```
$\label{eq97}{m_{X}}={{{x}^{4}}-{4 \ {r_{1}}\ {{x}^{3}}}+{6 \ {{r_{1}}^{2}}\ {{x}^{2}}}-{4 \ {{r_{1}}^{3}}\ x}+{{r_{1}}^{4}}}$ (97)

Type: Equation(Polynomial(Integer))

fricas
```
lhs eq4_2 = limit(limit(limit(rhs eq4_2,r[2]=r[1]),r[3]=r[1]),r[4]=r[1])
```
$\label{eq98}{g_{0}}={{{\left(-{{r_{1}}^{3}}+{3 \ {{r_{1}}^{2}}}-{6 \ {r_{1}}}+ 6 \right)}\ {{e}^{r_{1}}}}\over 6}$ (98)

Type: Equation(OrderedCompletion?(Expression(Integer)))

fricas
```
lhs eq4_3 = limit(limit(limit(rhs eq4_3,r[2]=r[1]),r[3]=r[1]),r[4]=r[1])
```
$\label{eq99}{g_{1}}={{{\left({{r_{1}}^{2}}-{2 \ {r_{1}}}+ 2 \right)}\ {{e}^{r_{1}}}}\over 2}$ (99)

Type: Equation(OrderedCompletion?(Expression(Integer)))

fricas
```
lhs eq4_4 = limit(limit(limit(rhs eq4_4,r[2]=r[1]),r[3]=r[1]),r[4]=r[1])
```
$\label{eq100}{g_{2}}={{{\left(-{r_{1}}+ 1 \right)}\ {{e}^{r_{1}}}}\over 2}$ (100)

Type: Equation(OrderedCompletion?(Expression(Integer)))

fricas
```
lhs eq4_5 = limit(limit(limit(rhs eq4_5,r[2]=r[1]),r[3]=r[1]),r[4]=r[1])
```
$\label{eq101}{g_{3}}={{{e}^{r_{1}}}\over 6}$ (101)

Type: Equation(OrderedCompletion?(Expression(Integer)))

... --Bill page, Wed, 24 Sep 2014 02:09:01 +0000 reply

SandBoxCollect