help links subscribe changes refresh edit

	SandBoxFunctionalSpecialFunction
	↑

SandBoxDiracDelta

last edited 10 years ago by Bill page

Edit detail for SandBoxDiracDelta revision 7 of 40

	1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40
Editor: Bill page Time: 2014/08/10 14:39:16 GMT+0
Note: bump function

changed:
-realDirac:=(eval(diracDelta(z),z=x+%i*y)+eval(diracDelta(z),z=x-%i*y))/2
realDirac:=(diracDelta(x+%i*y)+diracDelta(x-%i*y))/2

changed:
-  rule sqrt(-1)==msqrt(-1), _
-  rule -sqrt(-1)==-msqrt(-1) _
  rule sqrt(-1)*:a==msqrt(-1)*a, _
  rule -sqrt(-1)*:a==-msqrt(-1)*a _

removed:
-conj %
-conj %

removed:
---conj diracDelta(x+%i*y)

added:
limit(r1,y=0)

Load new definition of derivative of abs(x)

fricas

)lib FSPECX

   FunctionalSpecialFunction is now explicitly exposed in frame initial

   FunctionalSpecialFunction will be automatically loaded when needed 
      from /var/aw/var/LatexWiki/FSPECX.NRLIB/FSPECX

fricas

%signum:=differentiate(abs(%x),%x)

$\label{eq1}\%x \over{abs \left({\%x}\right)}$

(1)

Type: Expression(Integer)

fricas

signum(z)==eval(%signum,%x=z)

Type: Void

fricas

signum(x)

fricas

Compiling function signum with type Variable(x) -> Expression(
      Integer)

$\label{eq2}x \over{abs \left({x}\right)}$

(2)

Type: Expression(Integer)

fricas

%diracDelta:=differentiate(signum(%x),%x)

fricas

Compiling function signum with type Variable( ) -> Expression(
      Integer)

$\label{eq3}{{{abs \left({\%x}\right)}^{2}}-{{\%x}^{2}}}\over{{abs \left({\%x}\right)}^{3}}$

(3)

Type: Expression(Integer)

fricas

diracDelta(z)==eval(%diracDelta/2,%x=z)

Type: Void

fricas

diracDelta(x)

fricas

Compiling function diracDelta with type Variable(x) -> Expression(
      Integer)

$\label{eq4}{{{abs \left({x}\right)}^{2}}-{{x}^{2}}}\over{2 \ {{abs \left({x}\right)}^{3}}}$

(4)

Type: Expression(Integer)

fricas

realDirac:=(diracDelta(x+%i*y)+diracDelta(x-%i*y))/2

fricas

Compiling function diracDelta with type Polynomial(Complex(Integer))
       -> Expression(Complex(Integer))

$\label{eq5}{\left( \begin{array}{@{}l} \displaystyle {{\left({{abs \left({{i \ y}- x}\right)}^{2}}+{{y}^{2}}+{2 \ i \ x \ y}-{{x}^{2}}\right)}\ {{abs \left({{i \ y}+ x}\right)}^{3}}}+ \ \ \displaystyle {{{abs \left({{i \ y}- x}\right)}^{3}}\ {{abs \left({{i \ y}+ x}\right)}^{2}}}+ \ \ \displaystyle {{\left({{y}^{2}}-{2 \ i \ x \ y}-{{x}^{2}}\right)}\ {{abs \left({{i \ y}- x}\right)}^{3}}}$

(5)

Type: Expression(Complex(Integer))

fricas

msqrt:=operator('msqrt)

$\label{eq6}msqrt$

(6)

Type: BasicOperator?

fricas

conj1:Ruleset(Integer,Complex Integer,Expression Complex Integer) := ruleset([ _
  rule sqrt(-1)*:a==msqrt(-1)*a, _
  rule -sqrt(-1)*:a==-msqrt(-1)*a _
]$List RewriteRule(Integer,Complex Integer,Expression Complex Integer) )

$\label{eq7}\left\{{{i \ a}\mbox{\rm = =}{a \ {{{\tt'}msqrt}\left({- 1}\right)}}}, \:{-{i \ a}\mbox{\rm = =}-{a \ {{{\tt'}msqrt}\left({- 1}\right)}}}\right\}$

(7)

Type: Ruleset(Integer,Complex(Integer),Expression(Complex(Integer)))

fricas

conj2:RewriteRule(Integer,Complex Integer,Expression(Complex Integer)):= rule msqrt(-1)==-sqrt(-1)

$\label{eq8}{msqrt \left({- 1}\right)}\mbox{\rm = =}- i$

(8)

Type: RewriteRule?(Integer,Complex(Integer),Expression(Complex(Integer)))

fricas

conj(z)==conj2 conj1 z

Type: Void

fricas

conj(a+%i*b)

fricas

Compiling function conj with type Polynomial(Complex(Integer)) -> 
      Expression(Complex(Integer))

$\label{eq9}-{i \ b}+ a$

(9)

Type: Expression(Complex(Integer))

fricas

abs2sqrt:RewriteRule(Integer,Complex Integer,Expression(Complex Integer)):= rule abs(x)==sqrt(x*conj(x))

$\label{eq10}{abs \left({x}\right)}\mbox{\rm = =}{\sqrt{x \ {{{\tt'}conj}\left({x}\right)}}}$

(10)

Type: RewriteRule?(Integer,Complex(Integer),Expression(Complex(Integer)))

fricas

abs2sqrt(abs(a+%i*b))

fricas

Compiling function conj with type Expression(Complex(Integer)) -> 
      Expression(Complex(Integer))

$\label{eq11}\sqrt{{{b}^{2}}+{{a}^{2}}}$

(11)

Type: Expression(Complex(Integer))

fricas

r1:=abs2sqrt realDirac

$\label{eq12}{{{y}^{2}}\ {\sqrt{{{y}^{2}}+{{x}^{2}}}}}\over{{{y}^{4}}+{2 \ {{x}^{2}}\ {{y}^{2}}}+{{x}^{4}}}$

(12)

Type: Expression(Complex(Integer))

fricas

eval(realDirac,[x=0.1,y=1.0])::Float

$\label{eq13}0.9851853368_4157340165$

(13)

Type: Float

fricas

eval(r1,[x=0.1,y=1.0])::Float

$\label{eq14}0.9851853368_4157340165$

(14)

Type: Float

fricas

integrate(eval(r1,y=1),x=%minusInfinity..%plusInfinity,"noPole")

$\label{eq15}2$

(15)

Type: Union(f1: OrderedCompletion?(Expression(Complex(Integer))),...)

fricas

limit(r1,y=0)

$\label{eq16}0$

(16)

Type: Union(OrderedCompletion?(Expression(Complex(Integer))),...)

Properties

fricas

signum(x^2)

fricas

Compiling function signum with type Polynomial(Integer) -> 
      Expression(Integer)

$\label{eq17}{{x}^{2}}\over{abs \left({{x}^{2}}\right)}$

(17)

Type: Expression(Integer)

fricas

diracDelta(x)^2

$\label{eq18}{{{abs \left({x}\right)}^{4}}-{2 \ {{x}^{2}}\ {{abs \left({x}\right)}^{2}}}+{{x}^{4}}}\over{4 \ {{abs \left({x}\right)}^{6}}}$

(18)

Type: Expression(Integer)

fricas

diracDelta(x^2)

fricas

Compiling function diracDelta with type Polynomial(Integer) -> 
      Expression(Integer)

$\label{eq19}{{{abs \left({{x}^{2}}\right)}^{2}}-{{x}^{4}}}\over{2 \ {{abs \left({{x}^{2}}\right)}^{3}}}$

(19)

Type: Expression(Integer)

fricas

signum(x)*diracDelta(x)

$\label{eq20}{{x \ {{abs \left({x}\right)}^{2}}}-{{x}^{3}}}\over{2 \ {{abs \left({x}\right)}^{4}}}$

(20)

Type: Expression(Integer)

fricas

integrate(abs(x),x)

$\label{eq21}\int^{ \displaystyle x}{{abs \left({\%A}\right)}\ {d \%A}}$

(21)

Type: Union(Expression(Integer),...)

fricas

-- expected x*abs(x)/2
integrate(signum(x),x)

$\label{eq22}\int^{ \displaystyle x}{{\%A \over{abs \left({\%A}\right)}}\ {d \%A}}$

(22)

Type: Union(Expression(Integer),...)

fricas

-- expected abs(x)
integrate(diracDelta(x),x)

$\label{eq23}\int^{ \displaystyle x}{{{{{abs \left({\%A}\right)}^{2}}-{{\%A}^{2}}}\over{2 \ {{abs \left({\%A}\right)}^{3}}}}\ {d \%A}}$

(23)

Type: Union(Expression(Integer),...)

fricas

-- expected signum(x)/2
--
integrate(diracDelta(x),x=minusInfinity..plusInfinity,"noPole")

$\label{eq24}\mbox{\tt "failed"}$

(24)

Type: Union(fail: failed,...)

fricas

integrate(x*diracDelta(x),x=minusInfinity..plusInfinity,"noPole")

$\label{eq25}\mbox{\tt "failed"}$

(25)

Type: Union(fail: failed,...)

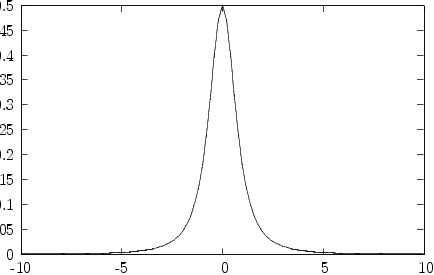
Bump function

fricas

)lib GDRAW

   GnuDraw is now explicitly exposed in frame initial 
   GnuDraw will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/GDRAW.NRLIB/GDRAW
X:=[(x/10)::DFLOAT for x in -100..100 by 2];

Type: List(DoubleFloat?)

fricas

Y:=[eval(r1,[x=x1,y=1.0])::DFLOAT for x1 in X];

Type: List(DoubleFloat?)

fricas

gnuDraw(X,Y,"SandBoxDiracDelta1.dat")

   Graph data being transmitted to the viewport manager...
   FriCAS2D data being transmitted to the viewport manager...

Type: Void

load "SandBoxDiracDelta1.dat"