help links subscribe changes refresh edit

	SandBox
SandBoxComplementsdalgebrelineaire ←	↑	→ SandBoxConditionalFunctions

SandBoxComplexManifold

Edit detail for SandBoxComplexManifold revision 7 of 7

	1 2 3 4 5 6 7
Editor: test1 Time: 2013/04/25 19:29:47 GMT+0
Note:

changed:
-ComplexManifold(R:Join(Field,RadicalCategory,TranscendentalFunctionCategory,OrderedSet)): Join(RadicalCategory,DirectProductCategory(2,R)) with
ComplexManifold(R:Join(Field, RadicalCategory, TranscendentalFunctionCategory, Comparable)
               ) : Join(RadicalCategory, DirectProductCategory(2,R)) with

changed:
-  == DirectProduct(2,R) add
  == DirectProduct(2, R) add

changed:
-    Rep == DirectProduct(2,R)
    Rep ==> DirectProduct(2,R)
    per x ==> (x@Rep) pretend %
    rep x ==> (x@%) pretend Rep


changed:
-      real(x)<0 and imag(x)=0 => pi()
      -- does not work since we have no order
      -- real(x)<0 and imag(x)=0 => pi()

added:
)set break resume

Complex domain constructor done differently.

DirectProduct? lifts many operations from the underlying domain automatically.

Complex values are represented as conjugate pairs.

fricas

(1) -> <spad>

fricas

)abbrev domain CM ComplexManifold
ComplexManifold(R:Join(Field, RadicalCategory, TranscendentalFunctionCategory, Comparable)
               ) : Join(RadicalCategory, DirectProductCategory(2,R)) with
    imaginary: () -> %
    real: % -> R
    imag: % -> R
    conj: % -> %
    norm: % -> R
    arg:  % -> R
    coerce: % -> Complex R
  == DirectProduct(2, R) add
    -- represent as conjugate pair
    Rep ==> DirectProduct(2,R)
    per x ==> (x@Rep) pretend %
    rep x ==> (x@%) pretend Rep

    pair(x:R,y:R):Rep == directProduct vector [x,y]
    dup(x:R):Rep == directProduct vector [x,x]
    import List R

    imaginary():% == per pair(1,-1)
    real(x:%):R == (rep(x).1 + rep(x).2)/(2::R)
    imag(x:%):R == (rep(x).1 - rep(x).2)/(2::R)
    -- just swap
    conj(x:%):% == per pair(rep(x).2,rep(x).1)
    -- multiplication is interesting
    (x:% * y:%):% == per pair( _
      real(x)*rep(y).1 + imag(x)*rep(y).2, _
      real(x)*rep(y).2 - imag(x)*rep(y).1)
    norm(x:%):R == retract(x*conj(x))
    iabs(x:%):R == sqrt norm x
    abs(x:%):% == per dup iabs x
    arg(x:%):R ==
      -- does not work since we have no order
      -- real(x)<0 and imag(x)=0 => pi()
      (2::R)*atan(imag(x)/(iabs(x)+real(x)))
    sqrt(x:%):% == per( sqrt(iabs(x))*pair( _
      cos(arg(x)/(2::R)) + sin(arg(x)/(2::R)), _
      cos(arg(x)/(2::R)) - sin(arg(x)/(2::R)) ) )

    coerce(x:%):OutputForm == complex(real x,imag x)$Complex(R)::OutputForm
    coerce(x:%):Complex(R) == complex(real x,imag x)</spad>

fricas

Compiling FriCAS source code from file 
      /var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/5781501376748542802-25px001.spad
      using old system compiler.
   CM abbreviates domain ComplexManifold 
------------------------------------------------------------------------
   initializing NRLIB CM for ComplexManifold 
   compiling into NRLIB CM 
****** Domain: R already in scope
****** Domain: R already in scope
****** Domain: R already in scope
   processing macro definition Rep ==> DirectProduct(2,R) 
   processing macro definition per x ==> pretend(@(x,DirectProduct(2,R)),%) 
   processing macro definition rep x ==> pretend(@(x,%),DirectProduct(2,R)) 
   compiling local pair : (R,R) -> DirectProduct(2,R)
Time: 0.03 SEC.

   compiling local dup : R -> DirectProduct(2,R)
Time: 0 SEC.

   importing List R
   compiling exported imaginary : () -> %
Time: 0 SEC.

   compiling exported real : % -> R
Time: 0 SEC.

   compiling exported imag : % -> R
Time: 0 SEC.

   compiling exported conj : % -> %
Time: 0 SEC.

   compiling exported * : (%,%) -> %
Time: 0 SEC.

   compiling exported norm : % -> R
Time: 0 SEC.

   compiling local iabs : % -> R
Time: 0 SEC.

   compiling local abs : % -> %
Time: 0 SEC.

   compiling exported arg : % -> R
Time: 0 SEC.

   compiling exported sqrt : % -> %
Time: 0 SEC.

   compiling exported coerce : % -> OutputForm
Time: 0 SEC.

   compiling exported coerce : % -> Complex R
Time: 0 SEC.

****** Domain: R already in scope
augmenting R: (OrderedSet)
****** Domain: R already in scope
augmenting R: (DifferentialRing)
****** Domain: R already in scope
augmenting R: (Evalable R)
****** Domain: R already in scope
augmenting R: (LinearlyExplicitOver (Integer))
****** Domain: R already in scope
augmenting R: (PartialDifferentialRing (Symbol))
****** Domain: R already in scope
augmenting R: (RetractableTo (Fraction (Integer)))
****** Domain: R already in scope
augmenting R: (RetractableTo (Integer))
****** Domain: % already in scope
augmenting %: (shallowlyMutable)
****** Domain: R already in scope
augmenting R: (Finite)
****** Domain: R already in scope
augmenting R: (OrderedAbelianMonoidSup)
****** Domain: R already in scope
augmenting R: (OrderedSet)
(time taken in buildFunctor:  75616)
Time: 0.10 SEC.

   Cumulative Statistics for Constructor ComplexManifold
      Time: 0.14 seconds

--------------non extending category----------------------
.. ComplexManifold(#1) of cat 
(|Join| (|RadicalCategory|) (|DirectProductCategory| 2 |#1|)
        (CATEGORY |domain| (SIGNATURE |imaginary| (%))
         (SIGNATURE |real| (|#1| %)) (SIGNATURE |imag| (|#1| %))
         (SIGNATURE |conj| (% %)) (SIGNATURE |norm| (|#1| %))
         (SIGNATURE |arg| (|#1| %)) (SIGNATURE |coerce| ((|Complex| |#1|) %))))   has no 
(|DirectProductCategory| NIL |#1|)    finalizing NRLIB CM 
   Processing ComplexManifold for Browser database:
--->-->ComplexManifold(constructor): Not documented!!!!
--->-->ComplexManifold((imaginary (%))): Not documented!!!!
--->-->ComplexManifold((real (R %))): Not documented!!!!
--->-->ComplexManifold((imag (R %))): Not documented!!!!
--->-->ComplexManifold((conj (% %))): Not documented!!!!
--->-->ComplexManifold((norm (R %))): Not documented!!!!
--->-->ComplexManifold((arg (R %))): Not documented!!!!
--->-->ComplexManifold((coerce ((Complex R) %))): Not documented!!!!
--->-->ComplexManifold(): Missing Description
; compiling file "/var/aw/var/LatexWiki/CM.NRLIB/CM.lsp" (written 24 SEP 2025 06:47:14 PM):

; wrote /var/aw/var/LatexWiki/CM.NRLIB/CM.fasl
; compilation finished in 0:00:00.044
------------------------------------------------------------------------
   ComplexManifold is now explicitly exposed in frame initial 
   ComplexManifold will be automatically loaded when needed from 
      /var/aw/var/LatexWiki/CM.NRLIB/CM

fricas

)show CM EXPR INT

 ComplexManifold(Expression(Integer)) is a domain constructor.
 Abbreviation for ComplexManifold is CM 
 This constructor is exposed in this frame.
 67 names for 103 operations in this domain.
------------------------------- Operations --------------------------------

 0 : () -> %                           1 : () -> %
 #? : % -> NonNegativeInteger          ?*? : (%, %) -> %
 ?*? : (%, Integer) -> %               ?*? : (Integer, %) -> %
 ?*? : (PositiveInteger, %) -> %       ?+? : (%, %) -> %
 -? : % -> %                           ?-? : (%, %) -> %
 ?=? : (%, %) -> Boolean               D : (%, List(Symbol)) -> %
 D : (%, Symbol) -> %                  ?^? : (%, PositiveInteger) -> %
 annihilate? : (%, %) -> Boolean       antiCommutator : (%, %) -> %
 arg : % -> Expression(Integer)        associator : (%, %, %) -> %
 coerce : % -> %                       coerce : Expression(Integer) -> %
 coerce : Fraction(Integer) -> %       coerce : Integer -> %
 coerce : % -> OutputForm              commutator : (%, %) -> %
 conj : % -> %                         copy : % -> %
 differentiate : (%, Symbol) -> %      empty : () -> %
 empty? : % -> Boolean                 eq? : (%, %) -> Boolean
 first : % -> Expression(Integer)      imag : % -> Expression(Integer)
 imaginary : () -> %                   index? : (Integer, %) -> Boolean
 indices : % -> List(Integer)          latex : % -> String
 maxIndex : % -> Integer               minIndex : % -> Integer
 norm : % -> Expression(Integer)       nthRoot : (%, Integer) -> %
 one? : % -> Boolean                   opposite? : (%, %) -> Boolean
 real : % -> Expression(Integer)       recip : % -> Union(%,"failed")
 retract : % -> Fraction(Integer)      retract : % -> Integer
 sample : () -> %                      sqrt : % -> %
 unitVector : PositiveInteger -> %     zero? : % -> Boolean
 ?~=? : (%, %) -> Boolean             
 ?*? : (%, Expression(Integer)) -> %
 ?*? : (Expression(Integer), %) -> %
 ?*? : (NonNegativeInteger, %) -> %
 D : (%, List(Symbol), List(NonNegativeInteger)) -> %
 D : (%, (Expression(Integer) -> Expression(Integer))) -> %
 D : (%, (Expression(Integer) -> Expression(Integer)), NonNegativeInteger) -> %
 D : (%, Symbol, NonNegativeInteger) -> %
 ?^? : (%, Fraction(Integer)) -> %
 ?^? : (%, NonNegativeInteger) -> %
 any? : ((Expression(Integer) -> Boolean), %) -> Boolean
 characteristic : () -> NonNegativeInteger
 coerce : % -> Complex(Expression(Integer))
 coerce : % -> Vector(Expression(Integer))
 count : (Expression(Integer), %) -> NonNegativeInteger
 count : ((Expression(Integer) -> Boolean), %) -> NonNegativeInteger
 differentiate : (%, List(Symbol)) -> %
 differentiate : (%, List(Symbol), List(NonNegativeInteger)) -> %
 differentiate : (%, (Expression(Integer) -> Expression(Integer))) -> %
 differentiate : (%, (Expression(Integer) -> Expression(Integer)), NonNegativeInteger) -> %
 differentiate : (%, Symbol, NonNegativeInteger) -> %
 directProduct : Vector(Expression(Integer)) -> %
 dot : (%, %) -> Expression(Integer)
 elt : (%, Integer) -> Expression(Integer)
 elt : (%, Integer, Expression(Integer)) -> Expression(Integer)
 entries : % -> List(Expression(Integer))
 entry? : (Expression(Integer), %) -> Boolean
 every? : ((Expression(Integer) -> Boolean), %) -> Boolean
 leftPower : (%, NonNegativeInteger) -> %
 leftPower : (%, PositiveInteger) -> %
 leftRecip : % -> Union(%,"failed")
 less? : (%, NonNegativeInteger) -> Boolean
 map : ((Expression(Integer) -> Expression(Integer)), %) -> %
 max : (((Expression(Integer), Expression(Integer)) -> Boolean), %) -> Expression(Integer)
 member? : (Expression(Integer), %) -> Boolean
 members : % -> List(Expression(Integer))
 more? : (%, NonNegativeInteger) -> Boolean
 parts : % -> List(Expression(Integer))
 plenaryPower : (%, PositiveInteger) -> %
 qelt : (%, Integer) -> Expression(Integer)
 reducedSystem : Matrix(%) -> Matrix(Expression(Integer))
 reducedSystem : Matrix(%) -> Matrix(Integer)
 reducedSystem : (Matrix(%), Vector(%)) -> Record(mat: Matrix(Expression(Integer)),vec: Vector(Expression(Integer)))
 reducedSystem : (Matrix(%), Vector(%)) -> Record(mat: Matrix(Integer),vec: Vector(Integer))
 retract : % -> Expression(Integer)
 retractIfCan : % -> Union(Expression(Integer),"failed")
 retractIfCan : % -> Union(Fraction(Integer),"failed")
 retractIfCan : % -> Union(Integer,"failed")
 rightPower : (%, NonNegativeInteger) -> %
 rightPower : (%, PositiveInteger) -> %
 rightRecip : % -> Union(%,"failed")
 size? : (%, NonNegativeInteger) -> Boolean
 subtractIfCan : (%, %) -> Union(%,"failed")

Compare:

fricas

)show COMPLEX EXPR INT

 Complex(Expression(Integer)) is a domain constructor.
 Abbreviation for Complex is COMPLEX 
 This constructor is exposed in this frame.
 114 names for 167 operations in this domain.
------------------------------- Operations --------------------------------

 0 : () -> %                           1 : () -> %
 ?*? : (%, %) -> %                     ?*? : (%, Integer) -> %
 ?*? : (Integer, %) -> %               ?*? : (PositiveInteger, %) -> %
 ?+? : (%, %) -> %                     -? : % -> %
 ?-? : (%, %) -> %                     ?/? : (%, %) -> %
 ?=? : (%, %) -> Boolean               D : (%, List(Symbol)) -> %
 D : (%, Symbol) -> %                  ?^? : (%, %) -> %
 ?^? : (%, Integer) -> %               ?^? : (%, PositiveInteger) -> %
 acos : % -> %                         acosh : % -> %
 acot : % -> %                         acoth : % -> %
 acsc : % -> %                         acsch : % -> %
 annihilate? : (%, %) -> Boolean       antiCommutator : (%, %) -> %
 asec : % -> %                         asech : % -> %
 asin : % -> %                         asinh : % -> %
 associates? : (%, %) -> Boolean       associator : (%, %, %) -> %
 atan : % -> %                         atanh : % -> %
 basis : () -> Vector(%)               coerce : % -> %
 coerce : Expression(Integer) -> %     coerce : Fraction(Integer) -> %
 coerce : Integer -> %                 coerce : % -> OutputForm
 commutator : (%, %) -> %              conjugate : % -> %
 convert : % -> InputForm              convert : % -> Pattern(Integer)
 cos : % -> %                          cosh : % -> %
 cot : % -> %                          coth : % -> %
 csc : % -> %                          csch : % -> %
 differentiate : (%, Symbol) -> %      exp : % -> %
 factor : % -> Factored(%)             gcd : (%, %) -> %
 gcd : List(%) -> %                    generator : () -> %
 imag : % -> Expression(Integer)       imaginary : () -> %
 inv : % -> %                          latex : % -> String
 lcm : (%, %) -> %                     lcm : List(%) -> %
 log : % -> %                          norm : % -> Expression(Integer)
 nthRoot : (%, Integer) -> %           one? : % -> Boolean
 opposite? : (%, %) -> Boolean         pi : () -> %
 prime? : % -> Boolean                 ?quo? : (%, %) -> %
 rank : () -> PositiveInteger          real : % -> Expression(Integer)
 recip : % -> Union(%,"failed")        ?rem? : (%, %) -> %
 retract : % -> Fraction(Integer)      retract : % -> Integer
 sample : () -> %                      sec : % -> %
 sech : % -> %                         sin : % -> %
 sinh : % -> %                         sizeLess? : (%, %) -> Boolean
 smaller? : (%, %) -> Boolean          sqrt : % -> %
 squareFree : % -> Factored(%)         squareFreePart : % -> %
 tan : % -> %                          tanh : % -> %
 trace : % -> Expression(Integer)      unit? : % -> Boolean
 unitCanonical : % -> %                zero? : % -> Boolean
 ?~=? : (%, %) -> Boolean             
 ?*? : (%, Expression(Integer)) -> %
 ?*? : (%, Fraction(Integer)) -> %
 ?*? : (Expression(Integer), %) -> %
 ?*? : (Fraction(Integer), %) -> %
 ?*? : (NonNegativeInteger, %) -> %
 D : (%, List(Symbol), List(NonNegativeInteger)) -> %
 D : (%, (Expression(Integer) -> Expression(Integer))) -> %
 D : (%, (Expression(Integer) -> Expression(Integer)), NonNegativeInteger) -> %
 D : (%, Symbol, NonNegativeInteger) -> %
 ?^? : (%, Fraction(Integer)) -> %
 ?^? : (%, NonNegativeInteger) -> %
 argument : % -> Expression(Integer)
 characteristic : () -> NonNegativeInteger
 characteristicPolynomial : % -> SparseUnivariatePolynomial(Expression(Integer))
 complex : (Expression(Integer), Expression(Integer)) -> %
 convert : SparseUnivariatePolynomial(Expression(Integer)) -> %
 convert : Vector(Expression(Integer)) -> %
 convert : % -> SparseUnivariatePolynomial(Expression(Integer))
 convert : % -> Vector(Expression(Integer))
 coordinates : Vector(%) -> Matrix(Expression(Integer))
 coordinates : (Vector(%), Vector(%)) -> Matrix(Expression(Integer))
 coordinates : % -> Vector(Expression(Integer))
 coordinates : (%, Vector(%)) -> Vector(Expression(Integer))
 definingPolynomial : () -> SparseUnivariatePolynomial(Expression(Integer))
 derivationCoordinates : (Vector(%), (Expression(Integer) -> Expression(Integer))) -> Matrix(Expression(Integer))
 differentiate : (%, List(Symbol)) -> %
 differentiate : (%, List(Symbol), List(NonNegativeInteger)) -> %
 differentiate : (%, (Expression(Integer) -> Expression(Integer))) -> %
 differentiate : (%, (Expression(Integer) -> Expression(Integer)), NonNegativeInteger) -> %
 differentiate : (%, Symbol, NonNegativeInteger) -> %
 discriminant : () -> Expression(Integer)
 discriminant : Vector(%) -> Expression(Integer)
 divide : (%, %) -> Record(quotient: %,remainder: %)
 euclideanSize : % -> NonNegativeInteger
 expressIdealMember : (List(%), %) -> Union(List(%),"failed")
 ?exquo? : (%, %) -> Union(%,"failed")
 ?exquo? : (%, Expression(Integer)) -> Union(%,"failed")
 extendedEuclidean : (%, %) -> Record(coef1: %,coef2: %,generator: %)
 extendedEuclidean : (%, %, %) -> Union(Record(coef1: %,coef2: %),"failed")
 factorPolynomial : SparseUnivariatePolynomial(%) -> Factored(SparseUnivariatePolynomial(%))
 factorSquareFreePolynomial : SparseUnivariatePolynomial(%) -> Factored(SparseUnivariatePolynomial(%))
 gcdPolynomial : (SparseUnivariatePolynomial(%), SparseUnivariatePolynomial(%)) -> SparseUnivariatePolynomial(%)
 lcmCoef : (%, %) -> Record(llcm_res: %,coeff1: %,coeff2: %)
 leftPower : (%, NonNegativeInteger) -> %
 leftPower : (%, PositiveInteger) -> %
 leftRecip : % -> Union(%,"failed")
 lift : % -> SparseUnivariatePolynomial(Expression(Integer))
 map : ((Expression(Integer) -> Expression(Integer)), %) -> %
 minimalPolynomial : % -> SparseUnivariatePolynomial(Expression(Integer))
 multiEuclidean : (List(%), %) -> Union(List(%),"failed")
 patternMatch : (%, Pattern(Integer), PatternMatchResult(Integer,%)) -> PatternMatchResult(Integer,%)
 plenaryPower : (%, PositiveInteger) -> %
 principalIdeal : List(%) -> Record(coef: List(%),generator: %)
 reduce : SparseUnivariatePolynomial(Expression(Integer)) -> %
 reduce : Fraction(SparseUnivariatePolynomial(Expression(Integer))) -> Union(%,"failed")
 reducedSystem : Matrix(%) -> Matrix(Expression(Integer))
 reducedSystem : Matrix(%) -> Matrix(Integer)
 reducedSystem : (Matrix(%), Vector(%)) -> Record(mat: Matrix(Expression(Integer)),vec: Vector(Expression(Integer)))
 reducedSystem : (Matrix(%), Vector(%)) -> Record(mat: Matrix(Integer),vec: Vector(Integer))
 regularRepresentation : % -> Matrix(Expression(Integer))
 regularRepresentation : (%, Vector(%)) -> Matrix(Expression(Integer))
 represents : Vector(Expression(Integer)) -> %
 represents : (Vector(Expression(Integer)), Vector(%)) -> %
 retract : % -> Expression(Integer)
 retractIfCan : % -> Union(Expression(Integer),"failed")
 retractIfCan : % -> Union(Fraction(Integer),"failed")
 retractIfCan : % -> Union(Integer,"failed")
 rightPower : (%, NonNegativeInteger) -> %
 rightPower : (%, PositiveInteger) -> %
 rightRecip : % -> Union(%,"failed")
 solveLinearPolynomialEquation : (List(SparseUnivariatePolynomial(%)), SparseUnivariatePolynomial(%)) -> Union(List(SparseUnivariatePolynomial(%)),"failed")
 squareFreePolynomial : SparseUnivariatePolynomial(%) -> Factored(SparseUnivariatePolynomial(%))
 subtractIfCan : (%, %) -> Union(%,"failed")
 traceMatrix : () -> Matrix(Expression(Integer))
 traceMatrix : Vector(%) -> Matrix(Expression(Integer))
 unitNormal : % -> Record(unit: %,canonical: %,associate: %)

Tests:

fricas

a:CM(EXPR INT) := 3

$\label{eq1}3$

(1)

Type: ComplexManifold?(Expression(Integer))

fricas

b:CM(EXPR INT) := -5

$\label{eq2}- 5$

(2)

Type: ComplexManifold?(Expression(Integer))

fricas

real(a)

$\label{eq3}3$

(3)

Type: Expression(Integer)

fricas

norm a

$\label{eq4}9$

(4)

Type: Expression(Integer)

fricas

norm b

$\label{eq5}25$

(5)

Type: Expression(Integer)

fricas

ab:=a*b

$\label{eq6}-{15}$

(6)

Type: ComplexManifold?(Expression(Integer))

fricas

real ab

$\label{eq7}-{15}$

(7)

Type: Expression(Integer)

fricas

imag ab

$\label{eq8}0$

(8)

Type: Expression(Integer)

fricas

s1:=sqrt(a)

$\label{eq9}\sqrt{3}$

(9)

Type: ComplexManifold?(Expression(Integer))

fricas

real s1

$\label{eq10}\sqrt{3}$

(10)

Type: Expression(Integer)

fricas

imag s1

$\label{eq11}0$

(11)

Type: Expression(Integer)

fricas

)set break resume

s2:=sqrt(b)

   >> Error detected within library code:
   catdef: division by zero

   Continuing to read the file...

real s2

$\label{eq12}s 2$

(12)

Type: Expression(Integer)

fricas

imag s2

$\label{eq13}0$

(13)

Type: Expression(Integer)

fricas

I:CM(EXPR INT) := imaginary()

$\label{eq14}i$

(14)

Type: ComplexManifold?(Expression(Integer))

fricas

real I

$\label{eq15}0$

(15)

Type: Expression(Integer)

fricas

norm I

$\label{eq16}1$

(16)

Type: Expression(Integer)

fricas

imag I

$\label{eq17}1$

(17)

Type: Expression(Integer)

fricas

imag conj I

$\label{eq18}- 1$

(18)

Type: Expression(Integer)

fricas

s3:=sqrt(I)

$\label{eq19}{\frac{\sqrt{2}}{2}}+{{\frac{\sqrt{2}}{2}}\ i}$

(19)

Type: ComplexManifold?(Expression(Integer))

fricas

s3*s3

$\label{eq20}i$

(20)

Type: ComplexManifold?(Expression(Integer))

fricas

c1:=conj(a+b*I)

$\label{eq21}3 +{5 \ i}$

(21)

Type: ComplexManifold?(Expression(Integer))

fricas

real c1

$\label{eq22}3$

(22)

Type: Expression(Integer)

fricas

imag c1

$\label{eq23}5$

(23)

Type: Expression(Integer)

fricas

norm c1

$\label{eq24}34$

(24)

Type: Expression(Integer)

fricas

c1::Complex(EXPR INT)

$\label{eq25}3 +{5 \ i}$

(25)

Type: Complex(Expression(Integer))

fricas

sqrt %

$\label{eq26}\begin{array}{@{}l} \displaystyle {\frac{\root{4}\of{34}}{\sqrt{\frac{{6 \ {\sqrt{34}}}+{68}}{{6 \ {\sqrt{34}}}+{43}}}}}+ \ \ \displaystyle {{\frac{5 \ {\root{4}\of{34}}}{{\left({\sqrt{34}}+ 3 \right)}\ {\sqrt{\frac{{6 \ {\sqrt{34}}}+{68}}{{6 \ {\sqrt{34}}}+{43}}}}}}\ i}$

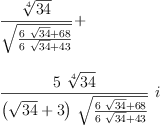(26)

Type: Complex(Expression(Integer))

fricas

s4:=sqrt(c1)

$\label{eq27}\begin{array}{@{}l} \displaystyle {\frac{\sqrt{\sqrt{34}}}{\sqrt{\frac{{6 \ {\sqrt{34}}}+{68}}{{6 \ {\sqrt{34}}}+{43}}}}}+ \ \ \displaystyle {{\frac{5 \ {\sqrt{\sqrt{34}}}}{{\left({\sqrt{34}}+ 3 \right)}\ {\sqrt{\frac{{6 \ {\sqrt{34}}}+{68}}{{6 \ {\sqrt{34}}}+{43}}}}}}\ i}$

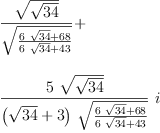(27)

Type: ComplexManifold?(Expression(Integer))

fricas

real s4

$\label{eq28}\frac{\sqrt{\sqrt{34}}}{\sqrt{\frac{{6 \ {\sqrt{34}}}+{68}}{{6 \ {\sqrt{34}}}+{43}}}}$

(28)

Type: Expression(Integer)

fricas

imag s4

$\label{eq29}\frac{5 \ {\sqrt{\sqrt{34}}}}{{\left({\sqrt{34}}+ 3 \right)}\ {\sqrt{\frac{{6 \ {\sqrt{34}}}+{68}}{{6 \ {\sqrt{34}}}+{43}}}}}$

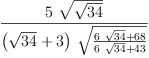(29)

Type: Expression(Integer)

fricas

s4*s4

$\label{eq30}3 +{5 \ i}$

(30)

Type: ComplexManifold?(Expression(Integer))

fricas

%::Complex(EXPR INT)

$\label{eq31}3 +{5 \ i}$

(31)

Type: Complex(Expression(Integer))

fricas

normalize %

$\label{eq32}{5 \ {\sqrt{- 1}}}+ 3$

(32)

Type: Expression(Integer)

fricas

%::Complex(EXPR INT)::Complex(INT)

   Cannot convert the value from type Complex(Expression(Integer)) to 
      Complex(Integer) .

   Continuing to read the file...