Works with ASCII text output formatting.
fricas
(1) -> )set output tex off
fricas
)set output algebra on
fricas
solve([x^2 + y^2 - 2*(ax*x + ay*y) = l1, x^2 + y^2 - 2*(cx*x + cy*y) = l2],[x,y])
(1)
[
(- 2 cy + 2 ay)y - l2 + l1
[x = --------------------------,
2 cx - 2 ax
2 2 2 2 2
(4 cy - 8 ay cy + 4 cx - 8 ax cx + 4 ay + 4 ax )y
+
2
(4 cy - 4 ay)l2 + (- 4 cy + 4 ay)l1 + (8 ax cx - 8 ax )cy
+
2
- 8 ay cx + 8 ax ay cx
*
y
+
2 2 2 2
l2 + (- 2 l1 + 4 ax cx - 4 ax )l2 + l1 + (- 4 cx + 4 ax cx)l1
=
0
]
]
Type: List(List(Equation(Fraction(Polynomial(Integer)))))
But fails with LaTeX.
fricas
)set output tex on
fricas
)set output algebra off
The result of
0^0 depends on the type of '0':
fricas
(0::Float)^(0::Float)
>> Error detected within library code:
0^0 is undefined
The idea was, that defining  as 1 is ok whenever there is no notion of limit. However,
as 1 is ok whenever there is no notion of limit. However,
fricas
(0::EXPR INT)^(0::EXPR INT)
Type: Expression(Integer)
is not quite in line with this, I think.
There has been some discussion on this subject on axiom-developer.
It is easy to change this behaviour, if we know better...
Let's see if the same happens here:
fricas
sinCosProducts := rule
sin (x) * sin (y) == (cos(x-y) - cos(x+y))/2
cos (x) * cos (y) == (cos(x-y) + cos(x+y))/2
sin (x) * cos (y) == (sin(x-y) + sin(x+y))/2
Type: Ruleset(Integer,Integer,Expression(Integer))
When you are typing or when you cut-and-paste commands directly
into the Axiom interpreter you must use an underscore character at
the end of each incomplete line, and you must use the ( ) syntax
instead of identation, like this:
sinCosProducts := rule (_
sin (x) * sin (y) == (cos(x-y) - cos(x+y))/2; _
cos (x) * cos (y) == (cos(x-y) + cos(x+y))/2; _
sin (x) * cos (y) == (sin(x-y) + sin(x+y))/2)
Alternatively, using a text editor you can enter the commands into a
file called, for example sincos.input exactly as in MathActon? above
and the use the command:
)read sincos.input
fricas
guess([1, 5, 14, 34, 69, 135, 240, 416, 686, 1106], [guessRat], [guessSum, guessProduct, guessOne])
Type: List(Expression(Integer))
Unknown wrote:
z:=sum(myfn(x),x=1..10) -- This fails, why?
The reason this fails is because Axiom tries to evaluate
myfn(x) first. But x is not yet an Integer so Axiom
cannot compute myfn(x). I guess you were expecting Axiom
to "wait" and not evaluate myfn(x) until after x has
been assigned the value 1, right? But Axiom does not work
this way.
The solution is to write myfn(x) so that is can be applied
to something symbolic like x. For example something this:
fricas
myfn(i : Expression Integer) : Expression Integer == i
Function declaration myfn : Expression(Integer) -> Expression(
Integer) has been added to workspace.
Type: Void
fricas
myfn(x)
fricas
Compiling function myfn with type Expression(Integer) -> Expression(
Integer)Type: Expression(Integer)
fricas
z:=sum(myfn(x),x=1..10)
Type: Expression(Integer)
Hi Bill:
Thanks for your quick response. I tried to respond to this earlier, but didn't see it in the sand box, please forgive me if you get multiple copies.
I tried to simplify the code from my original program, and generated a univariate function, however my actual code has a multivariate function,
and your excellent hint on the use of the Expression qualifier on the parameter and return type which works great for the univariate function case appears to fail for multivarite functions.
Please consider the following example.
fricas
a(n : Expression Integer, k : Expression Integer, p : Expression Float) : Expression Float == binomial(n,k) * p^(k) * (1.0-p)^(n-k)
Function declaration a : (Expression(Integer), Expression(Integer),
Expression(Float)) -> Expression(Float) has been added to
workspace.
Type: Void
fricas
output(a(4,3,0.25)) -- see that the function actually evaluates for sensible values
fricas
Compiling function a with type (Expression(Integer), Expression(
Integer), Expression(Float)) -> Expression(Float)
0.046875
Type: Void
fricas
z := sum(a(4,i,0.25), i=1..3) --- this fails
There are 6 exposed and 2 unexposed library operations named sum
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op sum
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named sum
with argument type(s)
Expression(Float)
SegmentBinding(PositiveInteger)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
I did notice in the Axiom online book, chapter 6.6, around page 241, the recommendation to use untyped functions, which appears to allow Axiom to do
inference on parameter and result type.
fricas
b(n, k, p) == binomial(n,k) * p^(k) * (1.0-p)^(n-k)
Type: Void
fricas
output(b(4,3,0.25)) -- see that the function actually evaluates for sensible values
fricas
Compiling function b with type (PositiveInteger, PositiveInteger,
Float) -> Float
0.046875
Type: Void
fricas
z := sum(b(4,i,0.25), i=1..3) --- this fails
fricas
Compiling function b with type (PositiveInteger, Variable(i), Float)
-> Expression(Float)
There are 6 exposed and 2 unexposed library operations named sum
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op sum
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named sum
with argument type(s)
Expression(Float)
SegmentBinding(PositiveInteger)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
For univariate functions the approach
fricas
c(k) == binomial(4,k) * 0.25^k * (1.0 - 0.25)^(4-k) -- This approach is only a test, but is not suitable for my program
Type: Void
fricas
output(c(3)) -- test to see if function can be evaluated for sensible arguments
fricas
Compiling function c with type PositiveInteger -> Float
0.046875
Type: Void
fricas
z := sum(c(i), i=1..3) -- still doesn't work
fricas
Compiling function c with type Variable(i) -> Expression(Float)
There are 6 exposed and 2 unexposed library operations named sum
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op sum
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named sum
with argument type(s)
Expression(Float)
SegmentBinding(PositiveInteger)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.But interestingly something like
fricas
d(k) == 1.5 * k -- coerce output to be a Float
Type: Void
fricas
z := sum(d(i), i=1..3) -- This works!
fricas
Compiling function d with type Variable(i) -> Polynomial(Float)
Type: Fraction(Polynomial(Float))
fricas
output(z)
9.0
Type: Void
Bill, thanks again for your quick help, unforutnatly I lack a local Axiom expert, any ideas would really be welcome here.
Try this
fricas
z := reduce(+,[b(4,i,0.25) for i in 1..3])
Type: Float
Hi all:
Thanks Bill Page for your help, it is much appreciated (although I used a for loop and not reduce :-)).
I'm having a bit of difficulty getting a Function returning a matrix to work as expected,
perhaps it is just cockpit error, but I don't see the error of my ways.
fricas
CFM(Q : Matrix(Float)): Matrix(Float) ==
x := nrows(Q)
MyIdentityMatrix : Matrix(Float) := new(x, x, 0)
for i in 1..nrows(MyIdentityMatrix) repeat
MyIdnetityMatrix(i,i) := 1.0
Ninv := MyIdnetityMatrix - Q
N := inverse(Ninv)
N
Function declaration CFM : Matrix(Float) -> Matrix(Float) has been
added to workspace.
Type: Void
fricas
--test ComputeFundamentalMatrix
X := matrix[[0, 0.5, 0],[0.5, 0, 0.5],[0, 0.5, 0]]
Type: Matrix(Float)
fricas
output(X)
+0.0 0.5 0.0+
| |
|0.5 0.0 0.5|
| |
+0.0 0.5 0.0+
Type: Void
fricas
N := CFM(X)
The form on the left hand side of an assignment must be a single
variable, a Tuple of variables or a reference to an entry in an
object supporting the setelt operation.
Any ideas where I'm blowing it here? I tried explicitly setting N to be a Matrix type but that failed too.
fricas
CFM(Q : Matrix(Float)): Matrix(Float) ==
x := nrows(Q)
MyIdentityMatrix : Matrix(Float) := new(x, x, 0)
for i in 1..nrows(MyIdentityMatrix) repeat
MyIdnetityMatrix(i,i) := 1.0
Ninv := MyIdnetityMatrix - Q
N := inverse(Ninv)
N
Function declaration CFM : Matrix(Float) -> Matrix(Float) has been
added to workspace.
Compiled code for CFM has been cleared.
1 old definition(s) deleted for function or rule CFM
Type: Void
fricas
--test ComputeFundamentalMatrix
X := matrix[[0, 0.5, 0],[0.5, 0, 0.5],[0, 0.5, 0]]
Type: Matrix(Float)
fricas
output(X)
+0.0 0.5 0.0+
| |
|0.5 0.0 0.5|
| |
+0.0 0.5 0.0+
Type: Void
fricas
N : Matrix(Float) := CFM(X)
The form on the left hand side of an assignment must be a single
variable, a Tuple of variables or a reference to an entry in an
object supporting the setelt operation.
Thanks again for all your help.
Regards:
Bill M. (Sorry, my unique last name attracts too much spam).
although I used a for loop and not reduce :-)
Good thinking. ;)
You have a simple typographical error. You have written both:
MyIdentityMatrix
and :
MyIdnetityMatrix
BTW, instead of the complicated construction of the identify matrix
you should just write:
Ninv := 1 - Q
For matrices 1 denotes the identity.
fricas
)set output tex off
fricas
)set output algebra on
FunFun := x^4 - 6* x^3 + 11* x^2 + 2* x + 1
4 3 2
(24) x - 6 x + 11 x + 2 x + 1
Type: Polynomial(Integer)
fricas
radicalSolve(FunFun)
(25)
[
x
=
-
ROOT
+------------------+2 +------------------+
| +----+ | +----+
| | 79 | | 79
- 3|144 |- -- + 2069 + 10 3|144 |- -- + 2069
\| \| 3 \| \| 3
+
- 169
*
+------------------------------------------------------+
| +------------------+2 +------------------+
| | +----+ | +----+
| | | 79 | | 79
|3|144 |- -- + 2069 + 5 3|144 |- -- + 2069 + 169
|\| \| 3 \| \| 3
|------------------------------------------------------
| +------------------+
| | +----+
| | | 79
| 3 3|144 |- -- + 2069
\| \| \| 3
+
+------------------+
| +----+
| | 79
- 48 3|144 |- -- + 2069
\| \| 3
/
+------------------+
| +----+
| | 79
3 3|144 |- -- + 2069
\| \| 3
*
+------------------------------------------------------+
| +------------------+2 +------------------+
| | +----+ | +----+
| | | 79 | | 79
|3|144 |- -- + 2069 + 5 3|144 |- -- + 2069 + 169
|\| \| 3 \| \| 3
|------------------------------------------------------
| +------------------+
| | +----+
| | | 79
| 3 3|144 |- -- + 2069
\| \| \| 3
+
+------------------------------------------------------+
| +------------------+2 +------------------+
| | +----+ | +----+
| | | 79 | | 79
|3|144 |- -- + 2069 + 5 3|144 |- -- + 2069 + 169
|\| \| 3 \| \| 3
|------------------------------------------------------ + 3
| +------------------+
| | +----+
| | | 79
| 3 3|144 |- -- + 2069
\| \| \| 3
/
2
,
x
=
ROOT
+------------------+2 +------------------+
| +----+ | +----+
| | 79 | | 79
(- 3|144 |- -- + 2069 + 10 3|144 |- -- + 2069 - 169)
\| \| 3 \| \| 3
*
+------------------------------------------------------+
| +------------------+2 +------------------+
| | +----+ | +----+
| | | 79 | | 79
|3|144 |- -- + 2069 + 5 3|144 |- -- + 2069 + 169
|\| \| 3 \| \| 3
|------------------------------------------------------
| +------------------+
| | +----+
| | | 79
| 3 3|144 |- -- + 2069
\| \| \| 3
+
+------------------+
| +----+
| | 79
- 48 3|144 |- -- + 2069
\| \| 3
/
+------------------+
| +----+
| | 79
3 3|144 |- -- + 2069
\| \| 3
*
+------------------------------------------------------+
| +------------------+2 +------------------+
| | +----+ | +----+
| | | 79 | | 79
|3|144 |- -- + 2069 + 5 3|144 |- -- + 2069 + 169
|\| \| 3 \| \| 3
|------------------------------------------------------
| +------------------+
| | +----+
| | | 79
| 3 3|144 |- -- + 2069
\| \| \| 3
+
+------------------------------------------------------+
| +------------------+2 +------------------+
| | +----+ | +----+
| | | 79 | | 79
|3|144 |- -- + 2069 + 5 3|144 |- -- + 2069 + 169
|\| \| 3 \| \| 3
|------------------------------------------------------ + 3
| +------------------+
| | +----+
| | | 79
| 3 3|144 |- -- + 2069
\| \| \| 3
/
2
,
x
=
-
ROOT
+------------------+2 +------------------+
| +----+ | +----+
| | 79 | | 79
- 3|144 |- -- + 2069 + 10 3|144 |- -- + 2069
\| \| 3 \| \| 3
+
- 169
*
+------------------------------------------------------+
| +------------------+2 +------------------+
| | +----+ | +----+
| | | 79 | | 79
|3|144 |- -- + 2069 + 5 3|144 |- -- + 2069 + 169
|\| \| 3 \| \| 3
|------------------------------------------------------
| +------------------+
| | +----+
| | | 79
| 3 3|144 |- -- + 2069
\| \| \| 3
+
+------------------+
| +----+
| | 79
48 3|144 |- -- + 2069
\| \| 3
/
+------------------+
| +----+
| | 79
3 3|144 |- -- + 2069
\| \| 3
*
+------------------------------------------------------+
| +------------------+2 +------------------+
| | +----+ | +----+
| | | 79 | | 79
|3|144 |- -- + 2069 + 5 3|144 |- -- + 2069 + 169
|\| \| 3 \| \| 3
|------------------------------------------------------
| +------------------+
| | +----+
| | | 79
| 3 3|144 |- -- + 2069
\| \| \| 3
+
+------------------------------------------------------+
| +------------------+2 +------------------+
| | +----+ | +----+
| | | 79 | | 79
|3|144 |- -- + 2069 + 5 3|144 |- -- + 2069 + 169
|\| \| 3 \| \| 3
- |------------------------------------------------------ + 3
| +------------------+
| | +----+
| | | 79
| 3 3|144 |- -- + 2069
\| \| \| 3
/
2
,
x
=
ROOT
+------------------+2 +------------------+
| +----+ | +----+
| | 79 | | 79
(- 3|144 |- -- + 2069 + 10 3|144 |- -- + 2069 - 169)
\| \| 3 \| \| 3
*
+------------------------------------------------------+
| +------------------+2 +------------------+
| | +----+ | +----+
| | | 79 | | 79
|3|144 |- -- + 2069 + 5 3|144 |- -- + 2069 + 169
|\| \| 3 \| \| 3
|------------------------------------------------------
| +------------------+
| | +----+
| | | 79
| 3 3|144 |- -- + 2069
\| \| \| 3
+
+------------------+
| +----+
| | 79
48 3|144 |- -- + 2069
\| \| 3
/
+------------------+
| +----+
| | 79
3 3|144 |- -- + 2069
\| \| 3
*
+------------------------------------------------------+
| +------------------+2 +------------------+
| | +----+ | +----+
| | | 79 | | 79
|3|144 |- -- + 2069 + 5 3|144 |- -- + 2069 + 169
|\| \| 3 \| \| 3
|------------------------------------------------------
| +------------------+
| | +----+
| | | 79
| 3 3|144 |- -- + 2069
\| \| \| 3
+
+------------------------------------------------------+
| +------------------+2 +------------------+
| | +----+ | +----+
| | | 79 | | 79
|3|144 |- -- + 2069 + 5 3|144 |- -- + 2069 + 169
|\| \| 3 \| \| 3
- |------------------------------------------------------ + 3
| +------------------+
| | +----+
| | | 79
| 3 3|144 |- -- + 2069
\| \| \| 3
/
2
]
Type: List(Equation(Expression(Integer)))
fricas
)set output tex on
fricas
)set output algebra off
Matthias
fricas
t:=matrix ([[0,1,1],[1,-2,2],[1,2,-1]])
Type: Matrix(Integer)
We can diagonalise t by finding it's eigenvalues.
fricas
)set output tex off
fricas
)set output algebra on
e:=radicalEigenvectors(t)
(27)
[
+-------------+2 +-------------+
| +------+ | +------+
| | 1345 | | 1345
| |- ---- + 3 | |- ---- + 3
|\| 3 |\| 3
3 3|------------- - 3 3|------------- + 7
\| 6 \| 6
[radval = --------------------------------------------, radmult = 1,
+-------------+
| +------+
| | 1345
| |- ---- + 3
|\| 3
3 3|-------------
\| 6
radvect = [matrix1]]
,
[
radval
=
+-------------+2
| +------+
| | 1345
| |- ---- + 3
+---+ |\| 3
(- 3 \|- 3 - 3) 3|-------------
\| 6
+
+-------------+
| +------+
| | 1345
| |- ---- + 3
+---+ |\| 3
(- 3 \|- 3 + 3) 3|------------- + 14
\| 6
/
+-------------+
| +------+
| | 1345
| |- ---- + 3
+---+ |\| 3
(3 \|- 3 - 3) 3|-------------
\| 6
,
radmult = 1, radvect = [matrix2]]
,
[
radval
=
+-------------+2
| +------+
| | 1345
| |- ---- + 3
+---+ |\| 3
(- 3 \|- 3 + 3) 3|-------------
\| 6
+
+-------------+
| +------+
| | 1345
| |- ---- + 3
+---+ |\| 3
(- 3 \|- 3 - 3) 3|------------- - 14
\| 6
/
+-------------+
| +------+
| | 1345
| |- ---- + 3
+---+ |\| 3
(3 \|- 3 + 3) 3|-------------
\| 6
,
radmult = 1, radvect = [matrix3]]
]
where matrix1
=
[
[
+-------------+2 +-------------+
| +------+ | +------+
| | 1345 | | 1345
| |- ---- + 3 +------+ | |- ---- + 3
|\| 3 | 1345 |\| 3
- 12 3|------------- + (6 |- ---- + 60) 3|-------------
\| 6 \| 3 \| 6
+
+------+
| 1345
3 |- ---- + 205
\| 3
/
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
126 3|-------------
\| 6
]
,
[
+-------------+2 +-------------+
| +------+ | +------+
| | 1345 | | 1345
| |- ---- + 3 +------+ | |- ---- + 3
|\| 3 | 1345 |\| 3
6 3|------------- + (- 3 |- ---- + 117) 3|-------------
\| 6 \| 3 \| 6
+
+------+
| 1345
9 |- ---- - 71
\| 3
/
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
126 3|-------------
\| 6
]
,
[1]]
and matrix2
=
[
[
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
- 24 3|-------------
\| 6
+
+-------------+
| +------+
| | 1345
+------+ +------+ | |- ---- + 3
| 1345 +---+ | 1345 |\| 3
((- 6 |- ---- - 60)\|- 3 - 6 |- ---- - 60) 3|-------------
\| 3 \| 3 \| 6
+
+------+ +------+
| 1345 +---+ | 1345
(3 |- ---- + 205)\|- 3 - 3 |- ---- - 205
\| 3 \| 3
/
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
252 3|-------------
\| 6
]
,
[
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
12 3|-------------
\| 6
+
+-------------+
| +------+
| | 1345
+------+ +------+ | |- ---- + 3
| 1345 +---+ | 1345 |\| 3
((3 |- ---- - 117)\|- 3 + 3 |- ---- - 117) 3|-------------
\| 3 \| 3 \| 6
+
+------+ +------+
| 1345 +---+ | 1345
(9 |- ---- - 71)\|- 3 - 9 |- ---- + 71
\| 3 \| 3
/
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
252 3|-------------
\| 6
]
,
[1]]
and matrix3
=
[
[
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
- 24 3|-------------
\| 6
+
+-------------+
| +------+
| | 1345
+------+ +------+ | |- ---- + 3
| 1345 +---+ | 1345 |\| 3
((6 |- ---- + 60)\|- 3 - 6 |- ---- - 60) 3|-------------
\| 3 \| 3 \| 6
+
+------+ +------+
| 1345 +---+ | 1345
(- 3 |- ---- - 205)\|- 3 - 3 |- ---- - 205
\| 3 \| 3
/
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
252 3|-------------
\| 6
]
,
[
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
12 3|-------------
\| 6
+
+-------------+
| +------+
| | 1345
+------+ +------+ | |- ---- + 3
| 1345 +---+ | 1345 |\| 3
((- 3 |- ---- + 117)\|- 3 + 3 |- ---- - 117) 3|-------------
\| 3 \| 3 \| 6
+
+------+ +------+
| 1345 +---+ | 1345
(- 9 |- ---- + 71)\|- 3 - 9 |- ---- + 71
\| 3 \| 3
/
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
252 3|-------------
\| 6
]
,
[1]]
Type: List(Record(radval: Expression(Integer),radmult: Integer,radvect: List(Matrix(Expression(Integer)))))
fricas
d:=diagonalMatrix([e.1.radval,e.2.radval,e.3.radval])
Function definition for d is being overwritten.
Compiled code for d has been cleared.
(28)
+-------------+2 +-------------+
| +------+ | +------+
| | 1345 | | 1345
| |- ---- + 3 | |- ---- + 3
|\| 3 |\| 3
3 3|------------- - 3 3|------------- + 7
\| 6 \| 6
[[--------------------------------------------, 0, 0],
+-------------+
| +------+
| | 1345
| |- ---- + 3
|\| 3
3 3|-------------
\| 6
[0,
+-------------+2
| +------+
| | 1345
| |- ---- + 3
+---+ |\| 3
(- 3 \|- 3 - 3) 3|-------------
\| 6
+
+-------------+
| +------+
| | 1345
| |- ---- + 3
+---+ |\| 3
(- 3 \|- 3 + 3) 3|------------- + 14
\| 6
/
+-------------+
| +------+
| | 1345
| |- ---- + 3
+---+ |\| 3
(3 \|- 3 - 3) 3|-------------
\| 6
,
0]
,
[0, 0,
+-------------+2
| +------+
| | 1345
| |- ---- + 3
+---+ |\| 3
(- 3 \|- 3 + 3) 3|-------------
\| 6
+
+-------------+
| +------+
| | 1345
| |- ---- + 3
+---+ |\| 3
(- 3 \|- 3 - 3) 3|------------- - 14
\| 6
/
+-------------+
| +------+
| | 1345
| |- ---- + 3
+---+ |\| 3
(3 \|- 3 + 3) 3|-------------
\| 6
]
]
Type: Matrix(Expression(Integer))
Now prove it by constructing the simularity transformation
from the eigenvectors:
fricas
p:=horizConcat(horizConcat(e.1.radvect.1,e.2.radvect.1),e.3.radvect.1)
(29)
[
[
+-------------+2 +-------------+
| +------+ | +------+
| | 1345 | | 1345
| |- ---- + 3 +------+ | |- ---- + 3
|\| 3 | 1345 |\| 3
- 12 3|------------- + (6 |- ---- + 60) 3|-------------
\| 6 \| 3 \| 6
+
+------+
| 1345
3 |- ---- + 205
\| 3
/
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
126 3|-------------
\| 6
,
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
- 24 3|-------------
\| 6
+
+-------------+
| +------+
| | 1345
+------+ +------+ | |- ---- + 3
| 1345 +---+ | 1345 |\| 3
((- 6 |- ---- - 60)\|- 3 - 6 |- ---- - 60) 3|-------------
\| 3 \| 3 \| 6
+
+------+ +------+
| 1345 +---+ | 1345
(3 |- ---- + 205)\|- 3 - 3 |- ---- - 205
\| 3 \| 3
/
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
252 3|-------------
\| 6
,
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
- 24 3|-------------
\| 6
+
+-------------+
| +------+
| | 1345
+------+ +------+ | |- ---- + 3
| 1345 +---+ | 1345 |\| 3
((6 |- ---- + 60)\|- 3 - 6 |- ---- - 60) 3|-------------
\| 3 \| 3 \| 6
+
+------+ +------+
| 1345 +---+ | 1345
(- 3 |- ---- - 205)\|- 3 - 3 |- ---- - 205
\| 3 \| 3
/
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
252 3|-------------
\| 6
]
,
[
+-------------+2 +-------------+
| +------+ | +------+
| | 1345 | | 1345
| |- ---- + 3 +------+ | |- ---- + 3
|\| 3 | 1345 |\| 3
6 3|------------- + (- 3 |- ---- + 117) 3|-------------
\| 6 \| 3 \| 6
+
+------+
| 1345
9 |- ---- - 71
\| 3
/
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
126 3|-------------
\| 6
,
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
12 3|-------------
\| 6
+
+-------------+
| +------+
| | 1345
+------+ +------+ | |- ---- + 3
| 1345 +---+ | 1345 |\| 3
((3 |- ---- - 117)\|- 3 + 3 |- ---- - 117) 3|-------------
\| 3 \| 3 \| 6
+
+------+ +------+
| 1345 +---+ | 1345
(9 |- ---- - 71)\|- 3 - 9 |- ---- + 71
\| 3 \| 3
/
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
252 3|-------------
\| 6
,
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
12 3|-------------
\| 6
+
+-------------+
| +------+
| | 1345
+------+ +------+ | |- ---- + 3
| 1345 +---+ | 1345 |\| 3
((- 3 |- ---- + 117)\|- 3 + 3 |- ---- - 117) 3|-------------
\| 3 \| 3 \| 6
+
+------+ +------+
| 1345 +---+ | 1345
(- 9 |- ---- + 71)\|- 3 - 9 |- ---- + 71
\| 3 \| 3
/
+-------------+2
| +------+
| | 1345
| |- ---- + 3
|\| 3
252 3|-------------
\| 6
]
,
[1, 1, 1]]
Type: Matrix(Expression(Integer))
fricas
p*d*inverse(p)
+0 1 1 +
| |
(30) |1 - 2 2 |
| |
+1 2 - 1+
Type: Matrix(Expression(Integer))
fricas
)set output tex on
fricas
)set output algebra off
\end{axiom}
Axiom can't integrame exp(x^4) ;(
fricas
integrate(exp(x^4),x)
Type: Union(Expression(Integer),...)
But Maple can...
fricas
f(x) == (1/4)*x*(-Gamma(1/4,-x^4)*Gamma(3/4)+%pi*sqrt(2))/((-x^4)^(1/4)*Gamma(3/4))
Type: Void
fricas
D(f(x),x)
fricas
Compiling function f with type Variable(x) -> Expression(Integer)
Type: Expression(Integer)
This is not a big surprise: note that
Gamma(x,y) is not an elementary function.
Martin
This was wrong:
fricas
integrate(1/(1+x^4),x=%minusInfinity..%plusInfinity)
Type: Union(f1: OrderedCompletion
?(Expression(Integer)),
...)
fricas
numeric(integrate(1/(1+x^4),x=0..1))
Type: Float
fricas
)clear co
All user variables and function definitions have been cleared.
All )browse facility databases have been cleared.
Internally cached functions and constructors have been cleared.
)clear completely is finished.
n := 32
fricas
y : FARRAY INT := new(n,1)
Type: FlexibleArray
?(Integer)
fricas
n0 := n
fricas
n1 := sum(x^1, x=0..n-1)
Type: Fraction(Polynomial(Integer))
fricas
n2 := sum(x^2, x=0..n-1)
Type: Fraction(Polynomial(Integer))
fricas
n3 := sum(x^3, x=0..n-1)
Type: Fraction(Polynomial(Integer))
fricas
n4 := sum(x^4, x=0..n-1)
Type: Fraction(Polynomial(Integer))
fricas
A := matrix([[n4, n3, n2],_
[n3, n2, n1],_
[n2, n1, n0]])
Type: Matrix(Fraction(Polynomial(Integer)))
fricas
X := vector([x1, x2, x3])
fricas
B := vector([sum(x^2* u, x=0..n-1),_
sum(x* v, x=0..n-1),_
sum( w, x=0..n-1)])
Type: Vector(Fraction(Polynomial(Integer)))
fricas
solve([A * X = B], [x1, x2, x3])
There are 20 exposed and 3 unexposed library operations named solve
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op solve
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named solve
with argument type(s)
List(Equation(Vector(Fraction(Polynomial(Integer)))))
List(OrderedVariableList([x1,x2,x3]))
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
fricas
integrate(1/((x+t)*sqrt(1+(x*t)^2)),t=0..%plusInfinity,"noPole")
Type: Union(f1: OrderedCompletion
?(Expression(Integer)),
...)
fricas
subst(%,x=1)
Type: Expression(Integer)
fricas
integrate(1/((1+t)*sqrt(1+(1*t)^2)),t=0..%plusInfinity,"noPole")
Type: Union(f1: OrderedCompletion
?(Expression(Integer)),
...)
fricas
simplify(%-subst((asinh(x^2)+asinh(1/x^2))/sqrt(1+x^4),x=1))
Type: Expression(Integer)
fricas
%::Expression Float
Type: Expression(Float)
fricas
a := matrix([ [-1,0,0,0,1,0], [0,1,0,0,0,0], [0,0,2,0,0,-2], [0,0,0,4,0,0], [0,0,0,0,3,0], [0,0,-3,0,0,3]])
Type: Matrix(Integer)
fricas
determinant(a)
Type: NonNegativeInteger
?
fricas
inverse(a)
Type: Union("failed",...)
fricas
As := matrix([ [-3,1,1,1], [1,1,1,1], [1,1,1,1], [1,1,1,1]])
Type: Matrix(Integer)
fricas
A := subMatrix(As, 2,4,2,4)
Type: Matrix(Integer)
fricas
ob := orthonormalBasis(A)
Type: List(Matrix(Expression(Integer)))
fricas
P : Matrix(Expression Integer) := new(3,3,0)
Type: Matrix(Expression(Integer))
fricas
setsubMatrix!(P,1,1,ob.3)
Type: Matrix(Expression(Integer))
fricas
setsubMatrix!(P,1,2,ob.1)
Type: Matrix(Expression(Integer))
fricas
setsubMatrix!(P,1,3,ob.2)
Type: Matrix(Expression(Integer))
fricas
Pt := transpose(P)
Type: Matrix(Expression(Integer))
fricas
Ps : Matrix(Expression Integer) := new(4,4,0)
Type: Matrix(Expression(Integer))
fricas
Ps(1,1) := 1
Type: Expression(Integer)
fricas
setsubMatrix!(Ps,2,2,P)
Type: Matrix(Expression(Integer))
fricas
PsT := transpose(Ps)
Type: Matrix(Expression(Integer))
fricas
PsTAsPs := PsT * As * Ps
Type: Matrix(Expression(Integer))
fricas
b1 := PsTAsPs(2,1)
Type: Expression(Integer)
fricas
l1 := PsTAsPs(2,2)
Type: Expression(Integer)
fricas
Us : Matrix(Expression Integer) := new(4,4,0)
Type: Matrix(Expression(Integer))
fricas
Us(1,1) := 1
Type: Expression(Integer)
fricas
Us(2,2) := 1
Type: Expression(Integer)
fricas
Us(3,3) := 1
Type: Expression(Integer)
fricas
Us(4,4) := 1
Type: Expression(Integer)
fricas
Us(2,1) := -b1 / l1
Type: Expression(Integer)
fricas
PsUs := Ps * Us
Type: Matrix(Expression(Integer))
fricas
PsUsT := transpose(PsUs)
Type: Matrix(Expression(Integer))
fricas
PsUsTAsPsUs := PsUsT * As * PsUs
Type: Matrix(Expression(Integer))
fricas
C := inverse(PsUs)
Type: Union(Matrix(Expression(Integer)),...)
fricas
c := PsUsTAsPsUs(1,1)
Type: Expression(Integer)
fricas
gQ := PsUsTAsPsUs / c
Type: Matrix(Expression(Integer))
fricas
x1 := transpose(matrix([[1,2,3,4]]))
Type: Matrix(Integer)
fricas
v1 := transpose(x1) * As * x1
Type: Matrix(Integer)
fricas
x2 := C * x1
Type: Matrix(Expression(Integer))
fricas
v2 := transpose(x2) * PsUsTAsPsUs * x2
Type: Matrix(Expression(Integer))
fricas
)clear all
All user variables and function definitions have been cleared.
draw(y^2/2+(x^2-1)^2/4-1=0, x,y, range ==[-2..2, -1..1])
Graph data being transmitted to the viewport manager...
FriCAS2D data being transmitted to the viewport manager...
Type: TwoDimensionalViewport
?
fricas
f1 := taylor(1 - x^2,x = 0)
Type: UnivariateTaylorSeries
?(Expression(Integer),
x,
0)
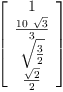
fricas
asin f1
Type: UnivariateTaylorSeries
?(Expression(Integer),
x,
0)
fricas
sin %
Type: UnivariateTaylorSeries
?(Expression(Integer),
x,
0)
SandboxMSkuce?
fricas
1+1
fricas
integrate((x-1)/log(x), x)
Type: Union(Expression(Integer),...)
fricas
integrate(x*exp(x)*sin(x),x)
Type: Union(Expression(Integer),...)
fricas
[p for p in primes(2,1000)|(p rem 16)=1]
Type: List(Integer)
fricas
[p^2+1 for p in primes(2,100)]
Type: List(Integer)
fricas
integrate (2*x^2 + 2*x, x)
Type: Polynomial(Fraction(Integer))
fricas
radix(36,37)
Type: RadixExpansion
?(37)
Is it error?
fricas
integrate(log(log(x)),x)
Type: Union(Expression(Integer),...)
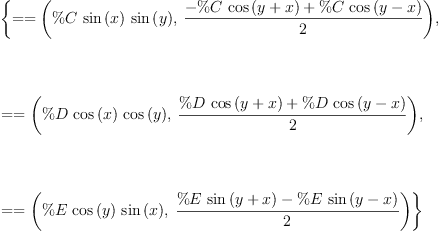



![\label{eq16}\begin{array}{@{}l}
\displaystyle
\left[ 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \right.
\
\
\displaystyle
\left.\: 1, \: 1, \: 1, \: 1, \: 1, \: 1 \right]
\label{eq16}\begin{array}{@{}l}
\displaystyle
\left[ 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \: 1, \right.
\
\
\displaystyle
\left.\: 1, \: 1, \: 1, \: 1, \: 1, \: 1 \right]](images/2939673866545044226-16.0px.png)





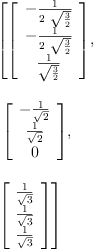

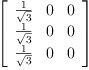
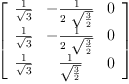
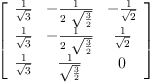
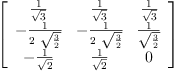

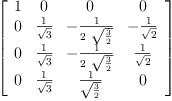
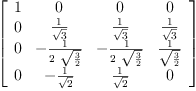
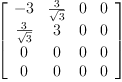

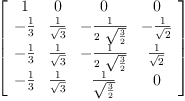
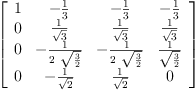

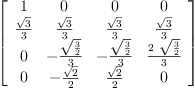
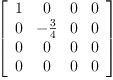
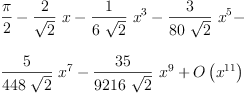
![\label{eq71}\begin{array}{@{}l}
\displaystyle
\left[{17}, \:{97}, \:{113}, \:{193}, \:{241}, \:{257}, \:{33
7}, \:{353}, \:{401}, \:{433}, \:{449}, \:{577}, \:{593}, \: \right.
\
\
\displaystyle
\left.{641}, \:{673}, \:{769}, \:{881}, \:{929}, \:{977}\right]
\label{eq71}\begin{array}{@{}l}
\displaystyle
\left[{17}, \:{97}, \:{113}, \:{193}, \:{241}, \:{257}, \:{33
7}, \:{353}, \:{401}, \:{433}, \:{449}, \:{577}, \:{593}, \: \right.
\
\
\displaystyle
\left.{641}, \:{673}, \:{769}, \:{881}, \:{929}, \:{977}\right]](images/2414374476207804480-16.0px.png)
![\label{eq72}\begin{array}{@{}l}
\displaystyle
\left[ 5, \:{10}, \:{26}, \:{50}, \:{122}, \:{170}, \:{290}, \:{362}, \:{530}, \:{842}, \:{962}, \:{1370}, \:{1682}, \: \right.
\
\
\displaystyle
\left.{1850}, \:{2210}, \:{2810}, \:{3482}, \:{3722}, \:{4490}, \:{5042}, \:{5330}, \:{6242}, \:{6890}, \: \right.
\
\
\displaystyle
\left.{7922}, \:{9410}\right]
\label{eq72}\begin{array}{@{}l}
\displaystyle
\left[ 5, \:{10}, \:{26}, \:{50}, \:{122}, \:{170}, \:{290}, \:{362}, \:{530}, \:{842}, \:{962}, \:{1370}, \:{1682}, \: \right.
\
\
\displaystyle
\left.{1850}, \:{2210}, \:{2810}, \:{3482}, \:{3722}, \:{4490}, \:{5042}, \:{5330}, \:{6242}, \:{6890}, \: \right.
\
\
\displaystyle
\left.{7922}, \:{9410}\right]](images/3011306311915716420-16.0px.png)