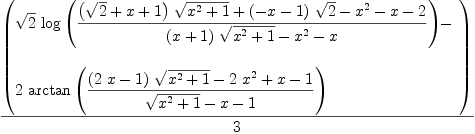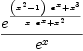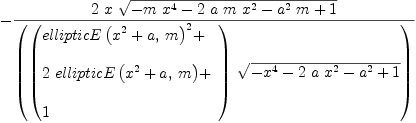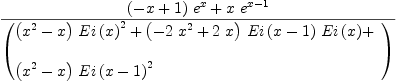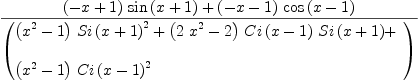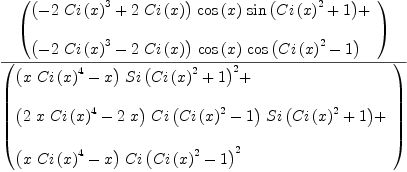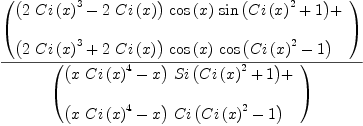help links subscribe changes refresh edit

	FriCAS
FriCASAdvantages ←	↑	→ SandBoxFriCAS

FriCASIntegration

Edit detail for FriCASIntegration revision 11 of 13

	1 2 3 4 5 6 7 8 9 10 11 12 13
Editor: test1 Time: 2022/05/04 17:06:25 GMT+0
Note:

changed:
-For example Maxma 5.41.1 can not handle
For example Maxma 5.45.1 can not handle

changed:
-Default integrators in Maple 15 and Maxima 5.41.1 can not handle
Default integrators in Maple 15 and Maxima 5.45.1 can not handle

FriCAS? inherited from Axiom implementation of Risch algorithm for elementary integration. It can handle both easy cases

fricas

integrate(x*exp(x^2), x)

$\label{eq1}{{e}^{{x}^{2}}}\over 2$

(1)

Type: Union(Expression(Integer),...)

fricas

integrate(exp(1/x^2)/x^3, x)

$\label{eq2}-{{{e}^{1 \over{{x}^{2}}}}\over 2}$

(2)

Type: Union(Expression(Integer),...)

and some which are hard for simpler algorithms. For example Maxma 5.45.1 can not handle

fricas

integrate(sqrt(x^2+1)/(x^3+1), x)

$\label{eq3}{\left( \begin{array}{@{}l} \displaystyle {{\sqrt{2}}\ {\log{\left({{{{\left({\sqrt{2}}+ x + 1 \right)}\ {\sqrt{{{x}^{2}}+ 1}}}+{{\left(- x - 1 \right)}\ {\sqrt{2}}}-{{x}^{2}}- x - 2}\over{{{\left(x + 1 \right)}\ {\sqrt{{{x}^{2}}+ 1}}}-{{x}^{2}}- x}}\right)}}}- \ \ \displaystyle {2 \ {\arctan \left({{{{\left({2 \ x}- 1 \right)}\ {\sqrt{{{x}^{2}}+ 1}}}-{2 \ {{x}^{2}}}+ x - 1}\over{{\sqrt{{{x}^{2}}+ 1}}- x - 1}}\right)}}$

(3)

Type: Union(Expression(Integer),...)

fricas

)set output tex off

fricas

)set output algebra on

integrate(sqrt(x^2+1)/(x^4+1), x)

   (4)
       -
              4+-+
            4 \|2
         *
            atan
                            +----------+
                            |   +-+
                   +-+      |2 \|2  - 4    4+-+
                 (\|2  - 1) |----------  - \|2
                            |   +-+
                           \|2 \|2  - 3
              /
                                +----------+
                                |   +-+
                       +-+      |2 \|2  - 4
                     (\|2  - 1) |----------
                                |   +-+
                               \|2 \|2  - 3
                  *
                     ROOT
                                                        +----------+
                                                        |   +-+
                                        +-+        4+-+ |2 \|2  - 4        3 +-+
                                (- 41 x\|2  + 58 x)\|2  |----------  - 48 x \|2
                                                        |   +-+
                                                       \|2 \|2  - 3
                              + 
                                    3
                                68 x
                           *
                               +------+
                               | 2
                              \|x  + 1
                          + 
                                                                +----------+
                                                                |   +-+
                                  2       +-+       2      4+-+ |2 \|2  - 4
                            ((41 x  + 17)\|2  - 58 x  - 24)\|2  |----------
                                                                |   +-+
                                                               \|2 \|2  - 3
                          + 
                                 +-+      4+-+2        4       2       +-+
                            (24 \|2  - 34)\|2   + (48 x  + 24 x  + 24)\|2
                          + 
                                  4       2
                            - 68 x  - 34 x  - 34
                       /
                              +-+
                          24 \|2  - 34
                 + 
                                 +----------+
                                 |   +-+      +------+
                        +-+      |2 \|2  - 4  | 2
                   (- x\|2  + x) |---------- \|x  + 1
                                 |   +-+
                                \|2 \|2  - 3
                 + 
                                 +----------+
                                 |   +-+
                     2 +-+    2  |2 \|2  - 4      +-+     4+-+
                   (x \|2  - x ) |----------  + (\|2  - 1)\|2
                                 |   +-+
                                \|2 \|2  - 3
     + 
           4+-+
         4 \|2
      *
         atan
                         +----------+
                         |   +-+
                +-+      |2 \|2  - 4    4+-+
              (\|2  - 1) |----------  + \|2
                         |   +-+
                        \|2 \|2  - 3
           /
                             +----------+
                             |   +-+
                    +-+      |2 \|2  - 4
                  (\|2  - 1) |----------
                             |   +-+
                            \|2 \|2  - 3
               *
                  ROOT
                                                   +----------+
                                                   |   +-+
                                   +-+        4+-+ |2 \|2  - 4        3 +-+
                             (41 x\|2  - 58 x)\|2  |----------  - 48 x \|2
                                                   |   +-+
                                                  \|2 \|2  - 3
                           + 
                                 3
                             68 x
                        *
                            +------+
                            | 2
                           \|x  + 1
                       + 
                                                               +----------+
                                                               |   +-+
                                 2       +-+       2      4+-+ |2 \|2  - 4
                         ((- 41 x  - 17)\|2  + 58 x  + 24)\|2  |----------
                                                               |   +-+
                                                              \|2 \|2  - 3
                       + 
                              +-+      4+-+2        4       2       +-+       4
                         (24 \|2  - 34)\|2   + (48 x  + 24 x  + 24)\|2  - 68 x
                       + 
                               2
                         - 34 x  - 34
                    /
                           +-+
                       24 \|2  - 34
              + 
                              +----------+                          +----------+
                              |   +-+      +------+                 |   +-+
                     +-+      |2 \|2  - 4  | 2          2 +-+    2  |2 \|2  - 4
                (- x\|2  + x) |---------- \|x  + 1  + (x \|2  - x ) |----------
                              |   +-+                               |   +-+
                             \|2 \|2  - 3                          \|2 \|2  - 3
              + 
                    +-+     4+-+
                (- \|2  + 1)\|2
     + 
           +-+     4+-+
         (\|2  - 1)\|2
      *
         log
                                         +----------+
                                         |   +-+
                         +-+        4+-+ |2 \|2  - 4        3 +-+       3
                  ((41 x\|2  - 58 x)\|2  |----------  - 48 x \|2  + 68 x )
                                         |   +-+
                                        \|2 \|2  - 3
               *
                   +------+
                   | 2
                  \|x  + 1
              + 
                                                      +----------+
                                                      |   +-+
                        2       +-+       2      4+-+ |2 \|2  - 4
                ((- 41 x  - 17)\|2  + 58 x  + 24)\|2  |----------
                                                      |   +-+
                                                     \|2 \|2  - 3
              + 
                     +-+      4+-+2        4       2       +-+       4       2
                (24 \|2  - 34)\|2   + (48 x  + 24 x  + 24)\|2  - 68 x  - 34 x
              + 
                - 34
           /
                  +-+
              24 \|2  - 34
     + 
             +-+     4+-+
         (- \|2  + 1)\|2
      *
         log
                                           +----------+
                                           |   +-+
                           +-+        4+-+ |2 \|2  - 4        3 +-+       3
                  ((- 41 x\|2  + 58 x)\|2  |----------  - 48 x \|2  + 68 x )
                                           |   +-+
                                          \|2 \|2  - 3
               *
                   +------+
                   | 2
                  \|x  + 1
              + 
                                                    +----------+
                                                    |   +-+
                      2       +-+       2      4+-+ |2 \|2  - 4
                ((41 x  + 17)\|2  - 58 x  - 24)\|2  |----------
                                                    |   +-+
                                                   \|2 \|2  - 3
              + 
                     +-+      4+-+2        4       2       +-+       4       2
                (24 \|2  - 34)\|2   + (48 x  + 24 x  + 24)\|2  - 68 x  - 34 x
              + 
                - 34
           /
                  +-+
              24 \|2  - 34
  /
                  +----------+
                  |   +-+
         +-+      |2 \|2  - 4
     (4 \|2  - 4) |----------
                  |   +-+
                 \|2 \|2  - 3

Type: Union(Expression(Integer),...)

fricas

)set output algebra off

fricas

)set output tex on

Default integrators in Mathematica 12.0 and Maple 15 can not handle

fricas

integrate(((exp(x)-x^2+2*x)/(x^2*(exp(x)+x)^2))*exp((x^2-1)/x+1/(exp(x)+x)), x)

$\label{eq4}{{e}^{{{{\left({{x}^{2}}- 1 \right)}\ {{e}^{x}}}+{{x}^{3}}}\over{{x \ {{e}^{x}}}+{{x}^{2}}}}}\over{{e}^{x}}$

(4)

Type: Union(Expression(Integer),...)

Default integrators in Maple 15 and Maxima 5.45.1 can not handle

fricas

integrate(x^6/sqrt((x^7+1)*(x^7+2)), x)

$\label{eq5}-{{\log \left({{2 \ {\sqrt{{{x}^{14}}+{3 \ {{x}^{7}}}+ 2}}}-{2 \ {{x}^{7}}}- 3}\right)}\over 7}$

(5)

Type: Union(Expression(Integer),...)

FriCAS? fixed several bugs in Axiom implementation, for example

fricas

integrate(cos(x)^n*sin(x)^(-n-2), x)

$\label{eq6}-{{{\cos \left({x}\right)}\ {\sin \left({x}\right)}\ {{e}^{{\left(- n - 2 \right)}\ {\log \left({\sin \left({x}\right)}\right)}}}\ {{e}^{n \ {\log \left({\cos \left({x}\right)}\right)}}}}\over{n + 1}}$

(6)

Type: Union(Expression(Integer),...)

fricas

integrate(exp(asec(x))/x^2, x)

$\label{eq7}{{\left({\sqrt{{{x}^{2}}- 1}}- 1 \right)}\ {{e}^{asec \left({x}\right)}}}\over{2 \ x}$

(7)

Type: Union(Expression(Integer),...)

work now but used to return unevaluated result.

Risch algorithm can handle large class of integrands involving special functions

fricas

f := D(1/(1 + ellipticE(x^2+a, m)), x)

$\label{eq8}\begin{array}{@{}l} \displaystyle -{{2 \ x \ {\sqrt{-{m \ {{x}^{4}}}-{2 \ a \ m \ {{x}^{2}}}-{{{a}^{2}}\ m}+ 1}}}\over{\left({\left({ \begin{array}{@{}l} \displaystyle {{ellipticE \left({{{{x}^{2}}+ a}, \: m}\right)}^{2}}+ \ \ \displaystyle {2 \ {ellipticE \left({{{{x}^{2}}+ a}, \: m}\right)}}+ \ \ \displaystyle 1$

(8)

Type: Expression(Integer)

fricas

integrate(f, x)

$\label{eq9}1 \over{{ellipticE \left({{{{x}^{2}}+ a}, \: m}\right)}+ 1}$

(9)

Type: Union(Expression(Integer),...)

fricas

f := D(1/(Ei(x)-Ei(x-1)), x)

$\label{eq10}{{{\left(- x + 1 \right)}\ {{e}^{x}}}+{x \ {{e}^{x - 1}}}}\over{\left( \begin{array}{@{}l} \displaystyle {{\left({{x}^{2}}- x \right)}\ {{Ei \left({x}\right)}^{2}}}+{{\left(-{2 \ {{x}^{2}}}+{2 \ x}\right)}\ {Ei \left({x - 1}\right)}\ {Ei \left({x}\right)}}+ \ \ \displaystyle {{\left({{x}^{2}}- x \right)}\ {{Ei \left({x - 1}\right)}^{2}}}$

(10)

Type: Expression(Integer)

fricas

integrate(f, x)

$\label{eq11}1 \over{{Ei \left({x}\right)}-{Ei \left({x - 1}\right)}}$

(11)

Type: Union(Expression(Integer),...)

fricas

f := D(1/(Si(x+1)+Ci(x-1)), x)

$\label{eq12}{{{\left(- x + 1 \right)}\ {\sin \left({x + 1}\right)}}+{{\left(- x - 1 \right)}\ {\cos \left({x - 1}\right)}}}\over{\left( \begin{array}{@{}l} \displaystyle {{\left({{x}^{2}}- 1 \right)}\ {{Si \left({x + 1}\right)}^{2}}}+{{\left({2 \ {{x}^{2}}}- 2 \right)}\ {Ci \left({x - 1}\right)}\ {Si \left({x + 1}\right)}}+ \ \ \displaystyle {{\left({{x}^{2}}- 1 \right)}\ {{Ci \left({x - 1}\right)}^{2}}}$

(12)

Type: Expression(Integer)

fricas

integrate(f, x)

$\label{eq13}1 \over{{Si \left({x + 1}\right)}+{Ci \left({x - 1}\right)}}$

(13)

Type: Union(Expression(Integer),...)

fricas

f := D(1/(Si(Ci(x)^2+1)+Ci(Ci(x)^2-1)), x)

$\label{eq14}{\left( \begin{array}{@{}l} \displaystyle {{\left(-{2 \ {{Ci \left({x}\right)}^{3}}}+{2 \ {Ci \left({x}\right)}}\right)}\ {\cos \left({x}\right)}\ {\sin \left({{{Ci \left({x}\right)}^{2}}+ 1}\right)}}+ \ \ \displaystyle {{\left(-{2 \ {{Ci \left({x}\right)}^{3}}}-{2 \ {Ci \left({x}\right)}}\right)}\ {\cos \left({x}\right)}\ {\cos \left({{{Ci \left({x}\right)}^{2}}- 1}\right)}}$

(14)

Type: Expression(Integer)

fricas

integrate(f, x)

$\label{eq15}1 \over{{Si \left({{{Ci \left({x}\right)}^{2}}+ 1}\right)}+{Ci \left({{{Ci \left({x}\right)}^{2}}- 1}\right)}}$

(15)

Type: Union(Expression(Integer),...)

fricas

f := D(log(Si(Ci(x)^2+1)+Ci(Ci(x)^2-1)), x)

$\label{eq16}{\left( \begin{array}{@{}l} \displaystyle {{\left({2 \ {{Ci \left({x}\right)}^{3}}}-{2 \ {Ci \left({x}\right)}}\right)}\ {\cos \left({x}\right)}\ {\sin \left({{{Ci \left({x}\right)}^{2}}+ 1}\right)}}+ \ \ \displaystyle {{\left({2 \ {{Ci \left({x}\right)}^{3}}}+{2 \ {Ci \left({x}\right)}}\right)}\ {\cos \left({x}\right)}\ {\cos \left({{{Ci \left({x}\right)}^{2}}- 1}\right)}}$

(16)

Type: Expression(Integer)

fricas

integrate(f, x)

$\label{eq17}\log \left({{Si \left({{{Ci \left({x}\right)}^{2}}+ 1}\right)}+{Ci \left({{{Ci \left({x}\right)}^{2}}- 1}\right)}}\right)$

(17)

Type: Union(Expression(Integer),...)

Alas, the following does not work

fricas

f := D(1/(1 + besselJ(m, x^2+a)), x)

$\label{eq18}{{x \ {besselJ \left({{m + 1}, \:{{{x}^{2}}+ a}}\right)}}-{x \ {besselJ \left({{m - 1}, \:{{{x}^{2}}+ a}}\right)}}}\over{{{besselJ \left({m , \:{{{x}^{2}}+ a}}\right)}^{2}}+{2 \ {besselJ \left({m , \:{{{x}^{2}}+ a}}\right)}}+ 1}$

(18)

Type: Expression(Integer)

fricas

integrate(f, x)

$\label{eq19}\int^{ \displaystyle x}{{{{\%A \ {besselJ \left({{m + 1}, \:{a +{{\%A}^{2}}}}\right)}}-{\%A \ {besselJ \left({{m - 1}, \:{a +{{\%A}^{2}}}}\right)}}}\over{{{besselJ \left({m , \:{a +{{\%A}^{2}}}}\right)}^{2}}+{2 \ {besselJ \left({m , \:{a +{{\%A}^{2}}}}\right)}}+ 1}}\ {d \%A}}$

(19)

Type: Union(Expression(Integer),...)

Risch algorithm wants to find elementary integral. For many functions integrals can be written only in terms of special function. FriCAS? now contains extensions which can handle some of them, see FriCASSpecialIntegration?.

For more elementary examples see FriCASTimofeev1?, FriCASTimofeev37?, FriCASTimofeev5?, FriCASTimofeev9?.

Examples involving exponential function from Albert Rich testsuite RichExp1?, RichExp2?.

integrate(exp(x-x^2), x) --mariuszi28cg, Mon, 25 Sep 2017 20:48:15 +0000 reply

fricas

integrate(exp(x-x^2), x)

$\label{eq20}{{{e}^{1 \over 4}}\ {\erf \left({{{2 \ x}- 1}\over 2}\right)}\ {\sqrt{\pi}}}\over 2$

(20)

Type: Union(Expression(Integer),...)