Evaluation may lead to spurious division by zero. This problem is not limited
to FriCAS, in fact it is general mathematical fact which limits what computers
(and people) can do. Simplest example is 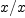 . When we plug in nonzero number
for
. When we plug in nonzero number
for 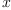 we get
we get 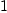 . However, plugging in
. However, plugging in 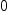 leads to division by
leads to division by 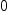 .
So, the expression
.
So, the expression 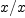 defines function different from
defines function different from 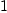 , namely
, namely 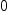 is not in the domain of function defined by
is not in the domain of function defined by 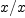 . For rational functions
we can easily limit the problem by canceling common divisors. FriCAS
expression domain is doing this auitomatically:
. For rational functions
we can easily limit the problem by canceling common divisors. FriCAS
expression domain is doing this auitomatically:
fricas
(1) -> sin(x)/sin(x)
Type: Expression(Integer)
Even for rational function we may still get into trouble in more complicated
situations. Consider 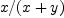 . Evaluation this at
. Evaluation this at 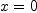 ,
, 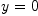 in
one step, that is as 'eval(x/(x + y), [x = 0, y = 0]?)' leads to division by
zero. OTOH evaluating in two steps gives value, but this value depends on
order of evaluation, first setting
in
one step, that is as 'eval(x/(x + y), [x = 0, y = 0]?)' leads to division by
zero. OTOH evaluating in two steps gives value, but this value depends on
order of evaluation, first setting 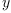 to
to 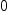 we get
we get 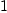 , while first
setting
, while first
setting 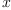 to
to 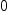 gives
gives 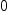 :
:
fricas
eval(x/(x + y), [y = 0])
Type: Fraction(Polynomial(Integer))
fricas
eval(x/(x + y), [x = 0])
Type: Fraction(Polynomial(Integer))
Problem becomes more complicated when we consider algebraic expression.
Take differential form 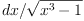 . This form have no
singularities on curve with equation
. This form have no
singularities on curve with equation 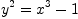 . More precisely,
to give well-defined meaning to square root we consider this curve.
Then
. More precisely,
to give well-defined meaning to square root we consider this curve.
Then 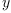 is square root of
is square root of 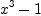 and our form is
and our form is 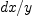 . In
. In
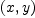 coordinates we have singularity when
coordinates we have singularity when 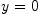 (and another singularity
at infinity). However, in different coordinates we can get nonsingular
expression at any given point. But we can not get coordinates good
for all points: for any fixed coordinate system there will be singular
points, even though for any point we can choose coordinate system
with no singularity at this point.
(and another singularity
at infinity). However, in different coordinates we can get nonsingular
expression at any given point. But we can not get coordinates good
for all points: for any fixed coordinate system there will be singular
points, even though for any point we can choose coordinate system
with no singularity at this point.
Algebraic expressions require care and computations may be tedious, but
at least in theory we can avoid division by 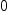 . However, in general it is
undecidable if a mathematical expression gives
. However, in general it is
undecidable if a mathematical expression gives 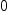 as a value. One approach
to this difficulty is to divide only by expressions which are known to be
non-zero. Applied naively this would severly limit possible computations.
FriCAS uses somewhat different approach: computations are normally done in
domains where we can decide if an expression is zero. However, such domain
may be different from domain intended by user. For example, in most operations
FriCAS treats Dirac delta "function" as transcendental quantity. This allows
computations which would make no sense from point of view of analysis. But
if final result is sensible (in partucular does not lead to division by
Dirac delta), then it is analytically correct.
as a value. One approach
to this difficulty is to divide only by expressions which are known to be
non-zero. Applied naively this would severly limit possible computations.
FriCAS uses somewhat different approach: computations are normally done in
domains where we can decide if an expression is zero. However, such domain
may be different from domain intended by user. For example, in most operations
FriCAS treats Dirac delta "function" as transcendental quantity. This allows
computations which would make no sense from point of view of analysis. But
if final result is sensible (in partucular does not lead to division by
Dirac delta), then it is analytically correct.
Similar approach deals with branches of multivalued functions: FriCAS works
with algebraic (or transcendental) extentions (fields). If element of an
extention is zero, then it is zero under any analytic interpretation (any
choice of branches). But specific choices of branches can lead to more
equalities. Still, if final result does not lead to division by zero,
then it is correct at least for some choice of branches.