help links subscribe changes refresh edit

	SandBox
DependentTypeTest2 ←	↑	→ DistributedExpression

DerivFunc

Edit detail for DerivFunc revision 2 of 2

	1 2
Editor: pagani Time: 2020/02/27 21:47:18 GMT+0
Note:

changed:
--- 
--- Derivatives of functions (Frechet derivative)
--- Sample: Lagrangian of a double pendulum
--- Ugly output of derivatives of (univariate) functions :( 
---
-
--- Macros
++ 
++ Functional derivatives  (Frechet derivative)
++ Sample: Lagrangian of a double pendulum
++ Ugly output of derivatives of (univariate) functions :( 
++

++ Macros



added:
eqL2x.1
eqL2x.2
eqL2y.1
eqL2y.2

fricas

(1) -> ++ 
++ Functional derivatives  (Frechet derivative)
++ Sample: Lagrangian of a double pendulum
++ Ugly output of derivatives of (univariate) functions :( 
++

++ Macros

macro mksn(s,n) == [s[i] for i in 1..n]

Type: Void

fricas

macro mks2 s == mksn(s,2)

Type: Void

fricas

macro mkeq(s,rhs) == [s.i=rhs.i for i in 1..#s]

Type: Void

fricas

-- Frechet derivative (functional derivative, req. for Lagrangian)
DF(f,g) == 
  s:=new()$Symbol -- generate new unique symbol
  fs:=subst(f,g=s)
  rs:=D(fs,s)
  r:=subst(rs,s=g)
  return r

Type: Void

fricas

-- test: DF(xt.1^n+sin xt.1,xt.1) 

-- Setup
q:=map(operator,mks2 q)

$\label{eq1}\left[{q_{1}}, \:{q_{2}}\right]$

(1)

Type: List(BasicOperator?)

fricas

x:=map(operator,mks2 x)

$\label{eq2}\left[{x_{1}}, \:{x_{2}}\right]$

(2)

Type: List(BasicOperator?)

fricas

y:=map(operator,mks2 y)

$\label{eq3}\left[{y_{1}}, \:{y_{2}}\right]$

(3)

Type: List(BasicOperator?)

fricas

l:=mks2 l

$\label{eq4}\left[{l_{1}}, \:{l_{2}}\right]$

(4)

Type: List(Symbol)

fricas

m:=mks2 m

$\label{eq5}\left[{m_{1}}, \:{m_{2}}\right]$

(5)

Type: List(Symbol)

fricas

-- Make functions of t
qt:=[f(t) for f in q]

$\label{eq6}\left[{{q_{1}}\left({t}\right)}, \:{{q_{2}}\left({t}\right)}\right]$

(6)

Type: List(Expression(Integer))

fricas

xt:=[f(t) for f in x]

$\label{eq7}\left[{{x_{1}}\left({t}\right)}, \:{{x_{2}}\left({t}\right)}\right]$

(7)

Type: List(Expression(Integer))

fricas

yt:=[f(t) for f in y]

$\label{eq8}\left[{{y_{1}}\left({t}\right)}, \:{{y_{2}}\left({t}\right)}\right]$

(8)

Type: List(Expression(Integer))

fricas

-- Geometry, equations for x1,y1,x2,y2
eqx:=mkeq(xt,[l.1*sin qt.1, l.1*sin qt.1 + l.2*sin qt.2])

$\label{eq9}\left[{{{x_{1}}\left({t}\right)}={{l_{1}}\ {\sin \left({{q_{1}}\left({t}\right)}\right)}}}, \:{{{x_{2}}\left({t}\right)}={{{l_{2}}\ {\sin \left({{q_{2}}\left({t}\right)}\right)}}+{{l_{1}}\ {\sin \left({{q_{1}}\left({t}\right)}\right)}}}}\right]$

(9)

Type: List(Equation(Expression(Integer)))

fricas

eqy:=mkeq(yt,[-l.1*cos qt.1, -l.1*cos qt.1 - l.2*cos qt.2])

$\label{eq10}\begin{array}{@{}l} \displaystyle \left[{{{y_{1}}\left({t}\right)}= -{{l_{1}}\ {\cos \left({{q_{1}}\left({t}\right)}\right)}}}, \: \right. \ \ \displaystyle \left.{{{y_{2}}\left({t}\right)}={-{{l_{2}}\ {\cos \left({{q_{2}}\left({t}\right)}\right)}}-{{l_{1}}\ {\cos \left({{q_{1}}\left({t}\right)}\right)}}}}\right]$

(10)

Type: List(Equation(Expression(Integer)))

fricas

-- All in a matrix
meqxy:= matrix [eqx,eqy]

$\label{eq11}\left[ \begin{array}{cc} {{{x_{1}}\left({t}\right)}={{l_{1}}\ {\sin \left({{q_{1}}\left({t}\right)}\right)}}}&{{{x_{2}}\left({t}\right)}={{{l_{2}}\ {\sin \left({{q_{2}}\left({t}\right)}\right)}}+{{l_{1}}\ {\sin \left({{q_{1}}\left({t}\right)}\right)}}}} \ {{{y_{1}}\left({t}\right)}= -{{l_{1}}\ {\cos \left({{q_{1}}\left({t}\right)}\right)}}}&{{{y_{2}}\left({t}\right)}={-{{l_{2}}\ {\cos \left({{q_{2}}\left({t}\right)}\right)}}-{{l_{1}}\ {\cos \left({{q_{1}}\left({t}\right)}\right)}}}}$

(11)

Type: Matrix(Equation(Expression(Integer)))

fricas

-- Potential energy
V:=operator 'V

$\label{eq12}V$

(12)

Type: BasicOperator?

fricas

eqV:=V(concat[xt,yt])=m.1*g*yt.1 + m.2*g*yt.2

$\label{eq13}{V \left({{{x_{1}}\left({t}\right)}, \:{{x_{2}}\left({t}\right)}, \:{{y_{1}}\left({t}\right)}, \:{{y_{2}}\left({t}\right)}}\right)}={{{m_{2}}\ g \ {{y_{2}}\left({t}\right)}}+{{m_{1}}\ g \ {{y_{1}}\left({t}\right)}}}$

(13)

Type: Equation(Expression(Integer))

fricas

-- Kinetic energy
T:=operator 'T

$\label{eq14}T$

(14)

Type: BasicOperator?

fricas

v:=D(matrix [xt,yt],t) -- velocities, col1=v1, col2=v2

$\label{eq15}\left[ \begin{array}{cc} {{{x_{1}}^{\prime}}\left({t}\right)}&{{{x_{2}}^{\prime}}\left({t}\right)} \ {{{y_{1}}^{\prime}}\left({t}\right)}&{{{y_{2}}^{\prime}}\left({t}\right)}$

(15)

Type: SquareMatrix?(2,Expression(Integer))

fricas

vv:=diagonal(transpose(v)*v)

$\label{eq16}\left[{{{{{y_{1}}^{\prime}}\left({t}\right)}^{2}}+{{{{x_{1}}^{\prime}}\left({t}\right)}^{2}}}, \:{{{{{y_{2}}^{\prime}}\left({t}\right)}^{2}}+{{{{x_{2}}^{\prime}}\left({t}\right)}^{2}}}\right]$

(16)

Type: DirectProduct?(2,Expression(Integer))

fricas

eqT:=T(concat listOfLists transpose v)=(1/2)*(m.1*vv.1 + m.2*vv.2)

$\label{eq17}\begin{array}{@{}l} \displaystyle {T \left({{{{x_{1}}^{\prime}}\left({t}\right)}, \:{{{y_{1}}^{\prime}}\left({t}\right)}, \:{{{x_{2}}^{\prime}}\left({t}\right)}, \:{{{y_{2}}^{\prime}}\left({t}\right)}}\right)}= \ \ \displaystyle {\frac{{{m_{2}}\ {{{{y_{2}}^{\prime}}\left({t}\right)}^{2}}}+{{m_{1}}\ {{{{y_{1}}^{\prime}}\left({t}\right)}^{2}}}+{{m_{2}}\ {{{{x_{2}}^{\prime}}\left({t}\right)}^{2}}}+{{m_{1}}\ {{{{x_{1}}^{\prime}}\left({t}\right)}^{2}}}}{2}}$

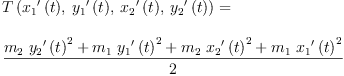(17)

Type: Equation(Expression(Integer))

fricas

-- DF(eqT,D(xt.1,t,1)) -> m1*x1'

-- Lagrangian L=T-V
L:=operator 'L

$\label{eq18}L$

(18)

Type: BasicOperator?

fricas

Largs:=concat [concat[xt,yt],concat listOfLists transpose v]

$\label{eq19}\begin{array}{@{}l} \displaystyle \left[{{x_{1}}\left({t}\right)}, \:{{x_{2}}\left({t}\right)}, \:{{y_{1}}\left({t}\right)}, \:{{y_{2}}\left({t}\right)}, \:{{{x_{1}}^{\prime}}\left({t}\right)}, \:{{{y_{1}}^{\prime}}\left({t}\right)}, \: \right. \ \ \displaystyle \left.{{{x_{2}}^{\prime}}\left({t}\right)}, \:{{{y_{2}}^{\prime}}\left({t}\right)}\right]$

(19)

Type: List(Expression(Integer))

fricas

eqL:=L(args)=rhs(eqT)-rhs(eqV)

$\label{eq20}\begin{array}{@{}l} \displaystyle {L \left({args}\right)}= \ \ \displaystyle {\frac{{{m_{2}}\ {{{{y_{2}}^{\prime}}\left({t}\right)}^{2}}}+{{m_{1}}\ {{{{y_{1}}^{\prime}}\left({t}\right)}^{2}}}+{{m_{2}}\ {{{{x_{2}}^{\prime}}\left({t}\right)}^{2}}}+{{m_{1}}\ {{{{x_{1}}^{\prime}}\left({t}\right)}^{2}}}-{2 \ {m_{2}}\ g \ {{y_{2}}\left({t}\right)}}-{2 \ {m_{1}}\ g \ {{y_{1}}\left({t}\right)}}}{2}}$

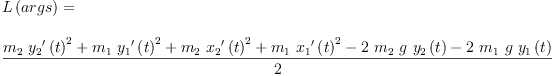(20)

Type: Equation(Expression(Integer))

fricas

-- Side conditions
sc1:=map(normalize, eqx.1^2 + eqy.1^2)

$\label{eq21}{{{{y_{1}}\left({t}\right)}^{2}}+{{{x_{1}}\left({t}\right)}^{2}}}={{l_{1}}^{2}}$

(21)

Type: Equation(Expression(Integer))

fricas

sc2:=map(normalize, (eqx.2-eqx.1)^2 + (eqy.2-eqy.1)^2)

$\label{eq22}\begin{array}{@{}l} \displaystyle {{{{y_{2}}\left({t}\right)}^{2}}-{2 \ {{y_{1}}\left({t}\right)}\ {{y_{2}}\left({t}\right)}}+{{{y_{1}}\left({t}\right)}^{2}}+{{{x_{2}}\left({t}\right)}^{2}}-{2 \ {{x_{1}}\left({t}\right)}\ {{x_{2}}\left({t}\right)}}+{{{x_{1}}\left({t}\right)}^{2}}}= \ \ \displaystyle {{l_{2}}^{2}}$

(22)

Type: Equation(Expression(Integer))

fricas

L2:=operator 'L2

$\label{eq23}L 2$

(23)

Type: BasicOperator?

fricas

eqL2:=L2(Largs)=rhs(eqT)-rhs(eqV)+A*(rhs(sc1)-lhs(sc1))+B*(rhs(sc2)-lhs(sc2))

$\label{eq24}\begin{array}{@{}l} \displaystyle {L 2 \left({{{x_{1}}\left({t}\right)}, \:{{x_{2}}\left({t}\right)}, \:{{y_{1}}\left({t}\right)}, \:{{y_{2}}\left({t}\right)}, \:{{{x_{1}}^{\prime}}\left({t}\right)}, \:{{{y_{1}}^{\prime}}\left({t}\right)}, \:{{{x_{2}}^{\prime}}\left({t}\right)}, \:{{{y_{2}}^{\prime}}\left({t}\right)}}\right)}= \ \ \displaystyle {\frac{{{m_{2}}\ {{{{y_{2}}^{\prime}}\left({t}\right)}^{2}}}+{{m_{1}}\ {{{{y_{1}}^{\prime}}\left({t}\right)}^{2}}}+{{m_{2}}\ {{{{x_{2}}^{\prime}}\left({t}\right)}^{2}}}+{{m_{1}}\ {{{{x_{1}}^{\prime}}\left({t}\right)}^{2}}}-{2 \ B \ {{{y_{2}}\left({t}\right)}^{2}}}+{{\left({4 \ B \ {{y_{1}}\left({t}\right)}}-{2 \ {m_{2}}\ g}\right)}\ {{y_{2}}\left({t}\right)}}+{{\left(-{2 \ B}-{2 \ A}\right)}\ {{{y_{1}}\left({t}\right)}^{2}}}-{2 \ {m_{1}}\ g \ {{y_{1}}\left({t}\right)}}-{2 \ B \ {{{x_{2}}\left({t}\right)}^{2}}}+{4 \ B \ {{x_{1}}\left({t}\right)}\ {{x_{2}}\left({t}\right)}}+{{\left(-{2 \ B}-{2 \ A}\right)}\ {{{x_{1}}\left({t}\right)}^{2}}}+{2 \ {{l_{2}}^{2}}\ B}+{2 \ {{l_{1}}^{2}}\ A}}{2}}$

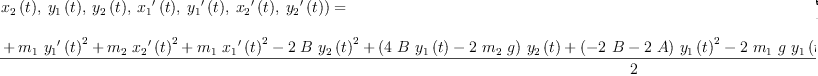(24)

Type: Equation(Expression(Integer))

fricas

-- Lagrange equations with SC
eqL2x:=[rhs(D(DF(eqL2,D(xt.i,t)),t)-DF(eqL2,xt.i))=0 for i in 1..2]

fricas

Compiling function DF with type (Equation(Expression(Integer)), 
      Expression(Integer)) -> Equation(Expression(Integer))

$\label{eq25}\begin{array}{@{}l} \displaystyle \left[{{{{m_{1}}\ {{{x_{1}}^{\prime \prime}}\left({t}\right)}}-{2 \ B \ {{x_{2}}\left({t}\right)}}+{{\left({2 \ B}+{2 \ A}\right)}\ {{x_{1}}\left({t}\right)}}}= 0}, \: \right. \ \ \displaystyle \left.{{{{m_{2}}\ {{{x_{2}}^{\prime \prime}}\left({t}\right)}}+{2 \ B \ {{x_{2}}\left({t}\right)}}-{2 \ B \ {{x_{1}}\left({t}\right)}}}= 0}\right]$

(25)

Type: List(Equation(Expression(Integer)))

fricas

eqL2y:=[rhs(D(DF(eqL2,D(yt.i,t)),t)-DF(eqL2,yt.i))=0 for i in 1..2]

$\label{eq26}\begin{array}{@{}l} \displaystyle \left[{ \begin{array}{@{}l} \displaystyle {{{m_{1}}\ {{{y_{1}}^{\prime \prime}}\left({t}\right)}}-{2 \ B \ {{y_{2}}\left({t}\right)}}+{{\left({2 \ B}+{2 \ A}\right)}\ {{y_{1}}\left({t}\right)}}+{{m_{1}}\ g}}= \ \ \displaystyle 0$

(26)

Type: List(Equation(Expression(Integer)))

fricas

eqL2x.1

$\label{eq27}{{{m_{1}}\ {{{x_{1}}^{\prime \prime}}\left({t}\right)}}-{2 \ B \ {{x_{2}}\left({t}\right)}}+{{\left({2 \ B}+{2 \ A}\right)}\ {{x_{1}}\left({t}\right)}}}= 0$

(27)

Type: Equation(Expression(Integer))

fricas

eqL2x.2

$\label{eq28}{{{m_{2}}\ {{{x_{2}}^{\prime \prime}}\left({t}\right)}}+{2 \ B \ {{x_{2}}\left({t}\right)}}-{2 \ B \ {{x_{1}}\left({t}\right)}}}= 0$

(28)

Type: Equation(Expression(Integer))

fricas

eqL2y.1

$\label{eq29}\begin{array}{@{}l} \displaystyle {{{m_{1}}\ {{{y_{1}}^{\prime \prime}}\left({t}\right)}}-{2 \ B \ {{y_{2}}\left({t}\right)}}+{{\left({2 \ B}+{2 \ A}\right)}\ {{y_{1}}\left({t}\right)}}+{{m_{1}}\ g}}= \ \ \displaystyle 0$

(29)

Type: Equation(Expression(Integer))

fricas

eqL2y.2

$\label{eq30}{{{m_{2}}\ {{{y_{2}}^{\prime \prime}}\left({t}\right)}}+{2 \ B \ {{y_{2}}\left({t}\right)}}-{2 \ B \ {{y_{1}}\left({t}\right)}}+{{m_{2}}\ g}}= 0$

(30)

Type: Equation(Expression(Integer))