login  home  contents  what's new  discussion  bug reports     help  links  subscribe  changes  refresh  edit
SandBox
DependentTypeTest2  ← ↑ →  DistributedExpression

DerivFunc
  
last edited 4 years ago by pagani

Edit detail for DerivFunc revision 1 of 2
1 2
Editor: pagani
Time: 2020/02/27 21:40:15 GMT+0
Note: 
changed:
-
\begin{axiom}

-- 
-- Derivatives of functions (Frechet derivative)
-- Sample: Lagrangian of a double pendulum
-- Ugly output of derivatives of (univariate) functions :( 
--

-- Macros
macro mksn(s,n) == [s[i] for i in 1..n]
macro mks2 s == mksn(s,2)
macro mkeq(s,rhs) == [s.i=rhs.i for i in 1..#s]

-- Frechet derivative (functional derivative, req. for Lagrangian)
DF(f,g) == 
  s:=new()$Symbol -- generate new unique symbol
  fs:=subst(f,g=s)
  rs:=D(fs,s)
  r:=subst(rs,s=g)
  return r

-- test: DF(xt.1^n+sin xt.1,xt.1) 

-- Setup
q:=map(operator,mks2 q) 
x:=map(operator,mks2 x)
y:=map(operator,mks2 y)
l:=mks2 l
m:=mks2 m

-- Make functions of t
qt:=[f(t) for f in q]
xt:=[f(t) for f in x]
yt:=[f(t) for f in y]

-- Geometry, equations for x1,y1,x2,y2
eqx:=mkeq(xt,[l.1*sin qt.1, l.1*sin qt.1 + l.2*sin qt.2])
eqy:=mkeq(yt,[-l.1*cos qt.1, -l.1*cos qt.1 - l.2*cos qt.2])

-- All in a matrix
meqxy:= matrix [eqx,eqy]

-- Potential energy
V:=operator 'V
eqV:=V(concat[xt,yt])=m.1*g*yt.1 + m.2*g*yt.2


-- Kinetic energy
T:=operator 'T
v:=D(matrix [xt,yt],t) -- velocities, col1=v1, col2=v2
vv:=diagonal(transpose(v)*v)
eqT:=T(concat listOfLists transpose v)=(1/2)*(m.1*vv.1 + m.2*vv.2)

-- DF(eqT,D(xt.1,t,1)) -> m1*x1'

-- Lagrangian L=T-V
L:=operator 'L
Largs:=concat [concat[xt,yt],concat listOfLists transpose v]
eqL:=L(args)=rhs(eqT)-rhs(eqV)

-- Side conditions
sc1:=map(normalize, eqx.1^2 + eqy.1^2)
sc2:=map(normalize, (eqx.2-eqx.1)^2 + (eqy.2-eqy.1)^2)
L2:=operator 'L2
eqL2:=L2(Largs)=rhs(eqT)-rhs(eqV)+A*(rhs(sc1)-lhs(sc1))+B*(rhs(sc2)-lhs(sc2))

-- Lagrange equations with SC
eqL2x:=[rhs(D(DF(eqL2,D(xt.i,t)),t)-DF(eqL2,xt.i))=0 for i in 1..2]
eqL2y:=[rhs(D(DF(eqL2,D(yt.i,t)),t)-DF(eqL2,yt.i))=0 for i in 1..2]





\end{axiom}
fricas
--
Derivatives of functions (Frechet derivative) -- Sample: Lagrangian of a double pendulum -- Ugly output of derivatives of (univariate) functions :( --
-- Macros macro mksn(s,n) == [s[i] for i in 1..n]
Type: Void
fricas
macro mks2 s == mksn(s,2)
Type: Void
fricas
macro mkeq(s,rhs) == [s.i=rhs.i for i in 1..#s]
Type: Void
fricas
-- Frechet derivative (functional derivative, req. for Lagrangian)
DF(f,g) == 
  s:=new()$Symbol -- generate new unique symbol
  fs:=subst(f,g=s)
  rs:=D(fs,s)
  r:=subst(rs,s=g)
  return r
Type: Void
fricas
-- test: DF(xt.1^n+sin xt.1,xt.1) 

-- Setup
q:=map(operator,mks2 q)
\label{eq1}\left[{q_{1}}, \:{q_{2}}\right](1)
Type: List(BasicOperator?)
fricas
x:=map(operator,mks2 x)
\label{eq2}\left[{x_{1}}, \:{x_{2}}\right](2)
Type: List(BasicOperator?)
fricas
y:=map(operator,mks2 y)
\label{eq3}\left[{y_{1}}, \:{y_{2}}\right](3)
Type: List(BasicOperator?)
fricas
l:=mks2 l
\label{eq4}\left[{l_{1}}, \:{l_{2}}\right](4)
Type: List(Symbol)
fricas
m:=mks2 m
\label{eq5}\left[{m_{1}}, \:{m_{2}}\right](5)
Type: List(Symbol)
fricas
-- Make functions of t
qt:=[f(t) for f in q]
\label{eq6}\left[{{q_{1}}\left({t}\right)}, \:{{q_{2}}\left({t}\right)}\right](6)
Type: List(Expression(Integer))
fricas
xt:=[f(t) for f in x]
\label{eq7}\left[{{x_{1}}\left({t}\right)}, \:{{x_{2}}\left({t}\right)}\right](7)
Type: List(Expression(Integer))
fricas
yt:=[f(t) for f in y]
\label{eq8}\left[{{y_{1}}\left({t}\right)}, \:{{y_{2}}\left({t}\right)}\right](8)
Type: List(Expression(Integer))
fricas
-- Geometry, equations for x1,y1,x2,y2
eqx:=mkeq(xt,[l.1*sin qt.1, l.1*sin qt.1 + l.2*sin qt.2])
\label{eq9}\left[{{{x_{1}}\left({t}\right)}={{l_{1}}\ {\sin \left({{q_{1}}\left({t}\right)}\right)}}}, \:{{{x_{2}}\left({t}\right)}={{{l_{2}}\ {\sin \left({{q_{2}}\left({t}\right)}\right)}}+{{l_{1}}\ {\sin \left({{q_{1}}\left({t}\right)}\right)}}}}\right](9)
Type: List(Equation(Expression(Integer)))
fricas
eqy:=mkeq(yt,[-l.1*cos qt.1, -l.1*cos qt.1 - l.2*cos qt.2])
\label{eq10}\begin{array}{@{}l} \displaystyle \left[{{{y_{1}}\left({t}\right)}= -{{l_{1}}\ {\cos \left({{q_{1}}\left({t}\right)}\right)}}}, \: \right. \ \ \displaystyle \left.{{{y_{2}}\left({t}\right)}={-{{l_{2}}\ {\cos \left({{q_{2}}\left({t}\right)}\right)}}-{{l_{1}}\ {\cos \left({{q_{1}}\left({t}\right)}\right)}}}}\right] (10)
Type: List(Equation(Expression(Integer)))
fricas
-- All in a matrix
meqxy:= matrix [eqx,eqy]
\label{eq11}\left[ \begin{array}{cc} {{{x_{1}}\left({t}\right)}={{l_{1}}\ {\sin \left({{q_{1}}\left({t}\right)}\right)}}}&{{{x_{2}}\left({t}\right)}={{{l_{2}}\ {\sin \left({{q_{2}}\left({t}\right)}\right)}}+{{l_{1}}\ {\sin \left({{q_{1}}\left({t}\right)}\right)}}}} \ {{{y_{1}}\left({t}\right)}= -{{l_{1}}\ {\cos \left({{q_{1}}\left({t}\right)}\right)}}}&{{{y_{2}}\left({t}\right)}={-{{l_{2}}\ {\cos \left({{q_{2}}\left({t}\right)}\right)}}-{{l_{1}}\ {\cos \left({{q_{1}}\left({t}\right)}\right)}}}} (11)
Type: Matrix(Equation(Expression(Integer)))
fricas
-- Potential energy
V:=operator 'V
\label{eq12}V(12)
Type: BasicOperator?
fricas
eqV:=V(concat[xt,yt])=m.1*g*yt.1 + m.2*g*yt.2
\label{eq13}{V \left({{{x_{1}}\left({t}\right)}, \:{{x_{2}}\left({t}\right)}, \:{{y_{1}}\left({t}\right)}, \:{{y_{2}}\left({t}\right)}}\right)}={{{m_{2}}\ g \ {{y_{2}}\left({t}\right)}}+{{m_{1}}\ g \ {{y_{1}}\left({t}\right)}}}(13)
Type: Equation(Expression(Integer))
fricas
-- Kinetic energy
T:=operator 'T
\label{eq14}T(14)
Type: BasicOperator?
fricas
v:=D(matrix [xt,yt],t) -- velocities, col1=v1, col2=v2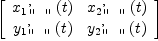
\label{eq15}\left[ \begin{array}{cc} {{{x_{1}}_{\verb#" "#}^{,}}\left({t}\right)}&{{{x_{2}}_{\verb#" "#}^{,}}\left({t}\right)} \ {{{y_{1}}_{\verb#" "#}^{,}}\left({t}\right)}&{{{y_{2}}_{\verb#" "#}^{,}}\left({t}\right)} (15)
Type: SquareMatrix?(2,Expression(Integer))
fricas
vv:=diagonal(transpose(v)*v)
\label{eq16}\begin{array}{@{}l} \displaystyle \left[{{{{{y_{1}}_{\verb#" "#}^{,}}\left({t}\right)}^{2}}+{{{{x_{1}}_{\verb#" "#}^{,}}\left({t}\right)}^{2}}}, \: \right. \ \ \displaystyle \left.{{{{{y_{2}}_{\verb#" "#}^{,}}\left({t}\right)}^{2}}+{{{{x_{2}}_{\verb#" "#}^{,}}\left({t}\right)}^{2}}}\right] (16)
Type: DirectProduct?(2,Expression(Integer))
fricas
eqT:=T(concat listOfLists transpose v)=(1/2)*(m.1*vv.1 + m.2*vv.2)
\label{eq17}\begin{array}{@{}l} \displaystyle {T \left({{{{x_{1}}_{\verb#" "#}^{,}}\left({t}\right)}, \:{{{y_{1}}_{\verb#" "#}^{,}}\left({t}\right)}, \:{{{x_{2}}_{\verb#" "#}^{,}}\left({t}\right)}, \:{{{y_{2}}_{\verb#" "#}^{,}}\left({t}\right)}}\right)}= \ \ \displaystyle {{\left( \begin{array}{@{}l} \displaystyle {{m_{2}}\ {{{{y_{2}}_{\verb#" "#}^{,}}\left({t}\right)}^{2}}}+{{m_{1}}\ {{{{y_{1}}_{\verb#" "#}^{,}}\left({t}\right)}^{2}}}+ \ \ \displaystyle {{m_{2}}\ {{{{x_{2}}_{\verb#" "#}^{,}}\left({t}\right)}^{2}}}+{{m_{1}}\ {{{{x_{1}}_{\verb#" "#}^{,}}\left({t}\right)}^{2}}} (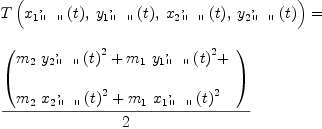17)
Type: Equation(Expression(Integer))
fricas
-- DF(eqT,D(xt.1,t,1)) -> m1*x1'

-- Lagrangian L=T-V
L:=operator 'L
\label{eq18}L(18)
Type: BasicOperator?
fricas
Largs:=concat [concat[xt,yt],concat listOfLists transpose v]
\label{eq19}\begin{array}{@{}l} \displaystyle \left[{{x_{1}}\left({t}\right)}, \:{{x_{2}}\left({t}\right)}, \:{{y_{1}}\left({t}\right)}, \:{{y_{2}}\left({t}\right)}, \:{{{x_{1}}_{\verb#" "#}^{,}}\left({t}\right)}, \:{{{y_{1}}_{\verb#" "#}^{,}}\left({t}\right)}, \right. \ \ \displaystyle \left.\:{{{x_{2}}_{\verb#" "#}^{,}}\left({t}\right)}, \:{{{y_{2}}_{\verb#" "#}^{,}}\left({t}\right)}\right] (19)
Type: List(Expression(Integer))
fricas
eqL:=L(args)=rhs(eqT)-rhs(eqV)
\label{eq20}\begin{array}{@{}l} \displaystyle {L \left({args}\right)}={{\left( \begin{array}{@{}l} \displaystyle {{m_{2}}\ {{{{y_{2}}_{\verb#" "#}^{,}}\left({t}\right)}^{2}}}+ \ \ \displaystyle {{m_{1}}\ {{{{y_{1}}_{\verb#" "#}^{,}}\left({t}\right)}^{2}}}+ \ \ \displaystyle {{m_{2}}\ {{{{x_{2}}_{\verb#" "#}^{,}}\left({t}\right)}^{2}}}+ \ \ \displaystyle {{m_{1}}\ {{{{x_{1}}_{\verb#" "#}^{,}}\left({t}\right)}^{2}}}-{2 \ {m_{2}}\ g \ {{y_{2}}\left({t}\right)}}- \ \ \displaystyle {2 \ {m_{1}}\ g \ {{y_{1}}\left({t}\right)}} (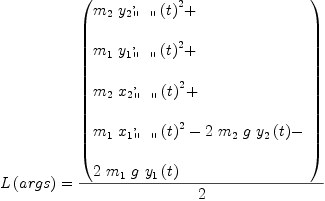20)
Type: Equation(Expression(Integer))
fricas
-- Side conditions
sc1:=map(normalize, eqx.1^2 + eqy.1^2)
\label{eq21}{{{{y_{1}}\left({t}\right)}^{2}}+{{{x_{1}}\left({t}\right)}^{2}}}={{l_{1}}^{2}}(21)
Type: Equation(Expression(Integer))
fricas
sc2:=map(normalize, (eqx.2-eqx.1)^2 + (eqy.2-eqy.1)^2)
\label{eq22}\begin{array}{@{}l} \displaystyle {{{{y_{2}}\left({t}\right)}^{2}}-{2 \ {{y_{1}}\left({t}\right)}\ {{y_{2}}\left({t}\right)}}+{{{y_{1}}\left({t}\right)}^{2}}+{{{x_{2}}\left({t}\right)}^{2}}-{2 \ {{x_{1}}\left({t}\right)}\ {{x_{2}}\left({t}\right)}}+{{{x_{1}}\left({t}\right)}^{2}}}= \ \ \displaystyle {{l_{2}}^{2}} (22)
Type: Equation(Expression(Integer))
fricas
L2:=operator 'L2
\label{eq23}L 2(23)
Type: BasicOperator?
fricas
eqL2:=L2(Largs)=rhs(eqT)-rhs(eqV)+A*(rhs(sc1)-lhs(sc1))+B*(rhs(sc2)-lhs(sc2))
\label{eq24}\begin{array}{@{}l} \displaystyle {L 2 \left({{{x_{1}}\left({t}\right)}, \:{{x_{2}}\left({t}\right)}, \:{{y_{1}}\left({t}\right)}, \:{{y_{2}}\left({t}\right)}, \:{{{x_{1}}_{\verb#" "#}^{,}}\left({t}\right)}, \:{{{y_{1}}_{\verb#" "#}^{,}}\left({t}\right)}, \:{{{x_{2}}_{\verb#" "#}^{,}}\left({t}\right)}, \:{{{y_{2}}_{\verb#" "#}^{,}}\left({t}\right)}}\right)}= \ \ \displaystyle {{\left( \begin{array}{@{}l} \displaystyle {{m_{2}}\ {{{{y_{2}}_{\verb#" "#}^{,}}\left({t}\right)}^{2}}}+{{m_{1}}\ {{{{y_{1}}_{\verb#" "#}^{,}}\left({t}\right)}^{2}}}+ \ \ \displaystyle {{m_{2}}\ {{{{x_{2}}_{\verb#" "#}^{,}}\left({t}\right)}^{2}}}+{{m_{1}}\ {{{{x_{1}}_{\verb#" "#}^{,}}\left({t}\right)}^{2}}}- \ \ \displaystyle {2 \ B \ {{{y_{2}}\left({t}\right)}^{2}}}+{{\left({4 \ B \ {{y_{1}}\left({t}\right)}}-{2 \ {m_{2}}\ g}\right)}\ {{y_{2}}\left({t}\right)}}+ \ \ \displaystyle {{\left(-{2 \ B}-{2 \ A}\right)}\ {{{y_{1}}\left({t}\right)}^{2}}}-{2 \ {m_{1}}\ g \ {{y_{1}}\left({t}\right)}}-{2 \ B \ {{{x_{2}}\left({t}\right)}^{2}}}+ \ \ \displaystyle {4 \ B \ {{x_{1}}\left({t}\right)}\ {{x_{2}}\left({t}\right)}}+{{\left(-{2 \ B}-{2 \ A}\right)}\ {{{x_{1}}\left({t}\right)}^{2}}}+{2 \ {{l_{2}}^{2}}\ B}+ \ \ \displaystyle {2 \ {{l_{1}}^{2}}\ A} (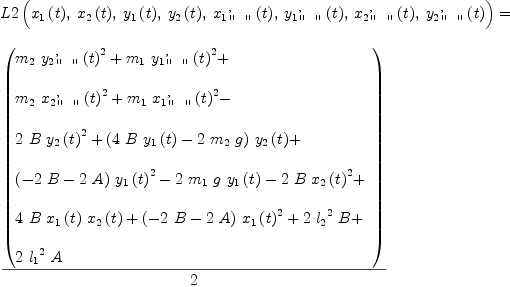24)
Type: Equation(Expression(Integer))
fricas
-- Lagrange equations with SC
eqL2x:=[rhs(D(DF(eqL2,D(xt.i,t)),t)-DF(eqL2,xt.i))=0 for i in 1..2]
fricas
Compiling function DF with type (Equation(Expression(Integer)), 
      Expression(Integer)) -> Equation(Expression(Integer))
\label{eq25}\begin{array}{@{}l} \displaystyle \left[{{{{m_{1}}\ {{{x_{1}}_{\verb#" "#}^{, ,}}\left({t}\right)}}-{2 \ B \ {{x_{2}}\left({t}\right)}}+{{\left({2 \ B}+{2 \ A}\right)}\ {{x_{1}}\left({t}\right)}}}= 0}, \: \right. \ \ \displaystyle \left.{{{{m_{2}}\ {{{x_{2}}_{\verb#" "#}^{, ,}}\left({t}\right)}}+{2 \ B \ {{x_{2}}\left({t}\right)}}-{2 \ B \ {{x_{1}}\left({t}\right)}}}= 0}\right] (25)
Type: List(Equation(Expression(Integer)))
fricas
eqL2y:=[rhs(D(DF(eqL2,D(yt.i,t)),t)-DF(eqL2,yt.i))=0 for i in 1..2]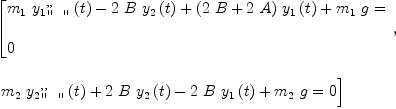
\label{eq26}\begin{array}{@{}l} \displaystyle \left[{ \begin{array}{@{}l} \displaystyle {{{m_{1}}\ {{{y_{1}}_{\verb#" "#}^{, ,}}\left({t}\right)}}-{2 \ B \ {{y_{2}}\left({t}\right)}}+{{\left({2 \ B}+{2 \ A}\right)}\ {{y_{1}}\left({t}\right)}}+{{m_{1}}\ g}}= \ \ \displaystyle 0 (26)
Type: List(Equation(Expression(Integer)))