|
|
|
last edited 17 years ago by kratt6 |
Edit detail for Common Mistakes revision 3 of 3
| 1 2 3 | ||
|
Editor: kratt6
Time: 2008/01/03 05:16:26 GMT-8 |
||
| Note: deindent 12 to make mathaction happy | ||
changed: - r:Fraction Integer:=1.544 - eq1:=90*%pi/180-asin(n*sin(34*%pi/180)/r)=asin(n/r) - s:=solve(eq1,n) - \end{axiom} r:Fraction Integer:=1.544 eq1:=90*%pi/180-asin(n*sin(34*%pi/180)/r)=asin(n/r) s:=solve(eq1,n) \end{axiom} changed: - eval(eq1,s.1)::Equation Expression Float - eval(eq1,s.2)::Equation Expression Float - \end{axiom} eval(eq1,s.1)::Equation Expression Float eval(eq1,s.2)::Equation Expression Float \end{axiom}
- Omitting the {axiom} enviroment
You have to use \begin{axiom} ... \end{axiom} or \begin{reduce} ... \end{reduce} before and after the command like this:
\begin{reduce} int(1/(a+z^3), z); \end{reduce} - Axiom commands do not end with ;
Oh yes, note that for Axiom you don't end the command with ; and the command for integration in Axiom is
integrate.fricas(1) -> integrate(1/(a+z^3),
z) 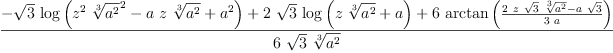
(1) Type: Union(Expression(Integer),...) - Reduce commands must end with a semicolon ;
But it must be there for Reduce.
r^2+r+1;
reduce 
- In Axiom
lnis writtenlogThis won't work:
\begin{axiom}integrate((x^2+2*x*ln(x)+5)/(sin(x^2+x^3-x^4)^2), x)\end{axiom}Put the \begin{axiom} and \end{axiom} on separate lines and notice that in Axiom
lnis writtenlogfricasintegrate((x^2+2*x*log(x)+5)/(sin(x^2+x^3-x^4)^2),
x) 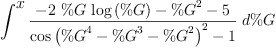
(2) Type: Union(Expression(Integer),...) - Don't put a \ in front of the axiom command
This is wrong:
\begin{axiom} \sqrt{49/100} \end{axiom}Begin each comment with an explanation. Don't put \ in front of the Axiom command.
Do it like this:
Some explanation \begin{axiom} sqrt{49/100} \end{axiom}Some explanation
fricassqrt{49/100}
(3) Type: AlgebraicNumber? - No $ before and after
This is wrong:
\begin{axiom} $ \sqrt{49/100} $ \end{axiom}Don't put $ before and after $ and there is no \ in front.
Just do it like this:
\begin{axiom} sqrt{49/100} \end{axiom}and what you will see is this:
fricassqrt{49/100}
(4) Type: AlgebraicNumber? - Axiom sometimes interprets commands in unexpected ways
This command appears to work
fricasintegrate(x^5 ln[x],
x) 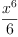
(5) Type: Union(Expression(Integer),...) But notice that
fricas5 ln[x]

(6) Type: UnivariatePolynomial(ln[x],Integer) is something strange. Oddly perhaps, Axiom interprets
5as a UnivariatePolynomial and 'ln[x]' as a subscripted Symbol and the result is a univariate polynomial in the variable 'ln[x]'.So perhaps what you meant to write was:
fricasintegrate(x^5*log(x),
x) 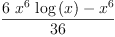
(7) Type: Union(Expression(Integer),...) - Use braces not parenthesis after
beginandendThe command:
\begin(axiom) integrate(sin(x)) \end(axiom)wont work.
Use "braces" like this { } not parenthesis ( ) around {axiom}.
Finally, unless the expression is a univariate polynomial, then you must also specify the variable with which to integrate.
fricasintegrate(sin(x),
x) 
(8) Type: Union(Expression(Integer),...) - Use parenthesis not braces in Axiom commands
This command:
\begin{axiom} solve{xy=1,x} \end{axiom}uses {} after the solve operation. This is syntactically correct but it probably doesn't do what you might expect.
fricassolve{xy=1,x} ![\label{eq9}\left[{x = 0}\right]
\label{eq9}\left[{x = 0}\right]](images/1785157559055029925-16.0px.png)
(9) Type: List(Equation(Fraction(Polynomial(Integer))))In Axiom {...,...} is executed as a block of commands which returns the result of the last command in the sequence. Compare
fricasa:={xy=1,x} 
(10) Type: Variable(x)which is just
xtofricasb:=(xy=1,
x) ![\label{eq11}\left[{xy = 1}, \: x \right]
\label{eq11}\left[{xy = 1}, \: x \right]](images/2409123706300253429-16.0px.png)
(11) Type: Tuple(Any)solve normally operates on such a tuple and
fricasc:=[xy=1,
x] ![\label{eq12}\left[{xy = 1}, \: x \right]
\label{eq12}\left[{xy = 1}, \: x \right]](images/7598437257676319802-16.0px.png)
(12) Type: List(Any)which is a list and finally
fricasc:=set [xy=1,
x] 
(13) Type: Set(Any)which is how to construct a set.
Also notice that multiplication must be written using *
fricassolve(x*y=1,
x) ![\label{eq14}\left[{x ={\frac{1}{y}}}\right]
\label{eq14}\left[{x ={\frac{1}{y}}}\right]](images/5682497115943164243-16.0px.png)
(14) Type: List(Equation(Fraction(Polynomial(Integer)))) - Use %minusInfinity and %plusInfinity
I'd like to see if Axiom can do my favorite definite integral:
\begin{axiom} integrate(x^4/(sinh(x))^2,x,-inf,inf) \end{axiom}In Axiom use %minusInfinity and %plusInfinity instead of -inf and inf.
fricasintegrate(x^4/(sinh(x))^2,
x=%minusInfinity..%plusInfinity) 
(15) Type: Union(pole: potentialPole,...) - Numeric conversions
The results of calculations depend on the type of the inputs You can tell Axiom that you would like the result expressed as a floating point number (if possible) using @. For example:
fricasasin(1/2)@Float

(16) Type: Float - Axiom prefers symbolic calculations
The trig functions are expressed in radians so use
 instead
instead
 and
and  instead of
instead of  . Finally, because Axiom
prefers symbolic calculations express
. Finally, because Axiom
prefers symbolic calculations express  as a rational number
fricas
as a rational number
fricasr:Fraction Integer:=1.544
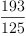
(17) Type: Fraction(Integer)fricaseq1:=90*%pi/180-asin(n*sin(34*%pi/180)/r)=asin(n/r)

(18) Type: Equation(Expression(Integer))fricass:=solve(eq1,
n) 
(19) Type: List(Equation(Expression(Integer)))Axiom thinks there are two solutions, unfortunately only one is valid:
fricaseval(eq1,
s.1)::Equation Expression Float 
(20) Type: Equation(Expression(Float))fricaseval(eq1,
s.2)::Equation Expression Float 
(21) Type: Equation(Expression(Float)) - Coercion is sometimes necessary
For example
fricasintegrate((4 - x**2)**.5::Expression Fraction Integer,
x)
There are no library operations named ** Use HyperDoc Browse or issue )what op ** to learn if there is any operation containing " ** " in its name.
Cannot find a definition or applicable library operation named ** with argument type(s) Variable(x) PositiveInteger
Perhaps you should use "@" to indicate the required return type,or "$" to specify which version of the function you need. - Use either
differentiateor the abbreviationDSince sin(x) cannot be interpreted as a univariate polynomial, you must specify the integration variable.
fricasdifferentiate(sin(x),
x) 
(22) Type: Expression(Integer) - MathAction requires that Axiom library code must beging with
)abbrev. Typing)abbis not enough even though that works in Axiom itself.