I make a list :

L := map (t +-> [t, divide (10*t,21)], expand (1..21-1))

(1)

I can't extract the second term :

fricas

select (t +-> t.1=2, L)

empty

(2)

Type: List(List(Any))

I get an error :

select (t +-> (t.2).remainder = 1, L)             -- erreur

   There are 1 exposed and 1 unexposed library operations named elt 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                               )display op elt
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.
   There are no library operations named G705 
      Use HyperDoc Browse or issue
                                )what op G705
      to learn if there is any operation containing " G705 " in its 
      name.
   There are 1 exposed and 1 unexposed library operations named elt 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                               )display op elt
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.
   There are 4 exposed and 1 unexposed library operations named select 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                             )display op select
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named 
      select with argument type(s) 
                              AnonymousFunction
                               List(List(Any))

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

It seems right :

Lc := reduce (append, L)

(3)

c := Lc.4

(4)

But I can't get the quotient :

c.quotient

   There are no library operations named c 
      Use HyperDoc Browse or issue
                                 )what op c
      to learn if there is any operation containing " c " in its name.

   Cannot find a definition or applicable library operation named c 
      with argument type(s) 
                             Variable(quotient)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

divide is right :

c2 := divide (20, 21)

(5)

c2.quotient

(6)

And all theses commands are right :

Lb := map (t +-> [t, (10*t) rem 21, (10*t) quo 21], expand (1..21-1))

(7)

select (t +-> t.1=2, Lb)

(8)

select (t +-> t.2 = 1, Lb)

(9)

reduce (append, Lb)

(10)

I don't know why but the result of

L := map (t +-> [t, divide (10*t,21)], expand (1..21-1))

(11)

is List List Any. So the interpreter seems to be smart to convert this back

K := first rest first L

(12)

to Record(quotient: Integer,remainder: Integer). But it only looks like that.

K.remainder

   There are no exposed library operations named K but there is one 
      unexposed operation with that name. Use HyperDoc Browse or issue
                                )display op K
      to learn more about the available operation.

   Cannot find a definition or applicable library operation named K 
      with argument type(s) 
                             Variable(remainder)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

gives an error. WHY?

A workaround is the following:

R := Record(quotient: Integer,remainder: Integer)

(13)

H := K :: R

(14)

H.remainder

(15)

Ralf

The internal types of these objects are of type Any but the interpreter uses the original types when it prints theses objects. See any.spad.pamphlet for information.

L := map (t +-> [t, divide (10*t,21)], expand (1..5))

(16)

Lc := reduce (append, L)

(17)

c := Lc.4

(18)

c

(19)

)display type c

   Type of value of c: Any
domainOf(c)

(20)

Status: open => closed

To extract second term use:

select(x+->x.1::Integer=2, L)

(21)

But I think the 2nd problem requiring the coercion to Record of something that is already apparently of that type is a bug.

L := map (t +-> makeRecord(t, divide (10*t,21)), expand (1..21-1))

(22)

select (t +-> t.part1=2, L)

(23)

select (t +-> (t.part2).remainder = 1, L)

(24)

L.2.part2.quotient

(25)

After reflexion I think I can't take the decision to close this bug report. First, some persons can prefer to have the real type displayed instead of the original one. Second, Bill Page thinks that the 2nd problem requiring the coercion to Record is a bug and third it's not possible to extract element of an object of type Any with Record as its original type but it's possible if the original type is List or Vector for example.

a:= [[x,2],4,divide(10,7)]

(26)

b:=a.1

(27)

)di type b

   Type of value of b: Any
b.1

(28)

c:=a.3

(29)

)di type c

   Type of value of c: Any
c.quotient

   There are no library operations named c 
      Use HyperDoc Browse or issue
                                 )what op c
      to learn if there is any operation containing " c " in its name.

   Cannot find a definition or applicable library operation named c 
      with argument type(s) 
                             Variable(quotient)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Status: closed => open

This command disables the display of the underlying type of an object of type Any.

)set message any

----------------------------- The any Option ------------------------------

 Description: print the internal type of objects of domain Any

 The any option may be followed by any one of the following:

 -> on 
    off

 The current setting is indicated within the list.

With this option off Axiom displays the Type: in the same way as )di type. This might be useful in order to avoid confusion in some cases.

Well, actually, this is one of the problem why people might find it hard to work with Axiom. Of course, Axiom returns for the best it could. If I write

ans := [2, divide(10*2,21)]

(30)

then it is clear that the type over which the list is formed have to be made equal. So we get List Any. But maybe, it would have been wiser if Axiom had warned about such a construction or Axiom should rather interpret the outer brackets in

[1, [2,3]]

(31)

as makeRecord.

makeRecord(1, [2,3])

(32)

Anyway, the question is also why someone wants to have

L := map (t +-> [t, divide (10*t,21)], expand (1..21-1));

in the first place. Wouldn't be

LL := map (t +-> divide (10*t,21), expand (1..21-1))

(33)

be sufficient? The argument is implicitly given through the list structure. And why not even just compute the following?

L3 := map (t +-> divide (10*t,21).remainder, expand (1..21-1))

(34)

And as for )set message any off is good (no confusion) and bad (no hint what one could do with the expression).

Of corse I can do

position (t +-> t.remainder=1, map (t +-> divide (10*t, 21), expand  (1..20)))

(35)

But (I believe) it's nearer the mathematical way to write

select (t +-> t.2.remainder=1, map (t +-> , expand (1..20)))

So I find all the solutions, and I remain the initial value which is right. It's as . Hier P(t)=t.2.remainder=1

Axiom believes that List are (almost) only in ,

With other CAS I use list as cartesian product of sets. It's very usefull and pretty to read.

With axiom I must use Record. If I use List I must explain that type I read (Record...) isn't type I have (Any...). It's to complex !

With record the length is fixed, and use of Record... is less pretty than use of List...

So I prefer that axiom-interpreter translates without question Any type to his own type. Even if there are difficults aroud this map : The first t is a Polynomial or an Integer ?

map (t +-> [t, X^t-1], expand (0..10))

(36)

FMy?

Don't you think that in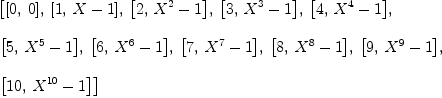 it depends on what your E is?

If you think that E is the set then something like

)clear all

   All user variables and function definitions have been cleared.
[t for e in 1..20 | (t:=divide(10*e,21); one?(t.remainder))]

(37)

looks quite mathematical, n'est pas? Well, there is a local assignment to , but it's short enough.

If you like your way more than perhaps write

K := [divide(10*t,21) for t in 1..20];

[t for t in K | t.remainder=1]

(38)

And, by the way, if it weren't for the fact that divide in Aldor's libalgebra library has signature:

  divide: (%, %) -> (%, %);

instead of Axiom's:

  divide: (%,%) -> Record(quotient:%,remainder:%)

The above construction would also work in Aldor. (The use of select is not possible since it is a reserved keyword in Aldor.)

Ralf

FMy?,

I think you meant to write:

select(t+->t.remainder=1,map (t +-> divide (10*t, 21), expand  (1..20)))

(39)

There is no meaning for t.2

I disagree that one should use a list as cartesian product of sets. This is very much against the strong-type design of Axiom. Instead Axom should provide a type equivalent to the cartesian product and it should be (nearly) as flexible as Lists. The next best thing that Axiom has is Record.

When creating an anonymous function you can provide specific types:

L:=map ((t:INT):Record(t:INT,p:POLY INT) +-> [t, X^t-1], expand (0..10))

(40)

so that the result is clear.

The discussion of Lists, Tuples, Products and Records in Axiom is an old one. See:

• http://axiom-wiki.newsynthesis.org/TuplesProductsAndRecords
• http://axiom-wiki.newsynthesis.org/SandBoxDirectProduct
• http://axiom-wiki.newsynthesis.org/187TroubleWithTuples
• http://axiom-wiki.newsynthesis.org/CartesianProduct

I agree that Axiom does not get this right. In Aldor the Product type is generalized to Cross.

I do not know yet how to understand the domain Any but I think it is very interesting. It is probably very close to what is called "duck typing" in modern terms:

http://en.wikipedia.org/wiki/Duck_typing

This a form of dynamic typing where the values from the domain Any carry with them their actual types. To me this seems like a "partially successful" early experiment with this idea - Another remarkable first for the Axiom developers! But it is only partially sucessful because all of the implications about how it should interact with the rest of the static strongly-typed language of Axiom is not fully worked out.

The switch showTypeInOutput can be used to show the underlying type of an object of type Any.

)set message any off

showTypeInOutput true

(41)

Test

a:Any:=[1,"a"]

(42)

a.1

(43)

(a.1)::Integer

(44)

(a.2)::String

(45)