Non-degeneracy of the pairing (snake relation)
or equivalently
Ref:
We use the Axiom LinearOperator library
fricas
(1) -> )library CARTEN MONAL PROP LOP
CartesianTensor is now explicitly exposed in frame initial
CartesianTensor will be automatically loaded when needed from
/var/aw/var/LatexWiki/CARTEN.NRLIB/CARTEN
Monoidal is now explicitly exposed in frame initial
Monoidal will be automatically loaded when needed from
/var/aw/var/LatexWiki/MONAL.NRLIB/MONAL
Prop is now explicitly exposed in frame initial
Prop will be automatically loaded when needed from
/var/aw/var/LatexWiki/PROP.NRLIB/PROP
>> System error:
The value
11722
is not of type
LIST
and some convenient notation
fricas
macro Σ(x,i,n)==reduce(+,[x for i in n])
Type: Void
fricas
macro Ξ(f,i,n)==[f for i in n]
Type: Void
fricas
macro sb == subscript
Type: Void
fricas
macro sp == superscript
Type: Void
Let 𝐋 be the domain of 2-dimensional linear operators
fricas
dim:=2
fricas
macro ℒ == List
Type: Void
fricas
macro ℚ == Expression Integer
Type: Void
fricas
𝐋 := LinearOperator(OVAR ['1,'2], ℚ)
There are no library operations named LinearOperator
Use HyperDoc Browse or issue
)what op LinearOperator
to learn if there is any operation containing " LinearOperator "
in its name.
Cannot find a definition or applicable library operation named
LinearOperator with argument type(s)
Type
Type
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
Pairing
A scalar product (pairing) is represented by
fricas
U:=Σ(Σ(sp('u,[i,j])*𝐝.i*𝐝.j, i,1..dim), j,1..dim)
There are no library operations named 𝐝
Use HyperDoc Browse or issue
)what op 𝐝
to learn if there is any operation containing " 𝐝 " in its name.
Cannot find a definition or applicable library operation named 𝐝
with argument type(s)
PositiveInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
FriCAS will attempt to step through and interpret the code.
There are no library operations named 𝐝
Use HyperDoc Browse or issue
)what op 𝐝
to learn if there is any operation containing " 𝐝 " in its name.
Cannot find a definition or applicable library operation named 𝐝
with argument type(s)
PositiveInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
In general we do not require that it be symmetric.
Co-pairing
Solve the "twisted snake relation" as a system of linear equations.
fricas
Ω:𝐋:=Σ(Σ(sb('u,[i,j])*𝐞.i*𝐞.j, i,1..dim), j,1..dim)
𝐋 is not a valid type.
This is equivalent to a matrix inverse (transposed!)
fricas
Um:=matrix Ξ(Ξ((𝐞.i*𝐞.j)/U, i,1..dim), j,1..dim)
There are no library operations named 𝐞
Use HyperDoc Browse or issue
)what op 𝐞
to learn if there is any operation containing " 𝐞 " in its name.
Cannot find a definition or applicable library operation named 𝐞
with argument type(s)
PositiveInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
FriCAS will attempt to step through and interpret the code.
There are no library operations named 𝐞
Use HyperDoc Browse or issue
)what op 𝐞
to learn if there is any operation containing " 𝐞 " in its name.
Cannot find a definition or applicable library operation named 𝐞
with argument type(s)
PositiveInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
Check that the twisted snake relation holds
fricas
test
( I Ω ) /
( I X ) /
( U I ) = I
There are no exposed library operations named I but there is one
unexposed operation with that name. Use HyperDoc Browse or issue
)display op I
to learn more about the available operation.
Cannot find a definition or applicable library operation named I
with argument type(s)
Variable(Ω)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
Dimension
Since the "snake" is twisted, dimension is as expected.
fricas
d:=
Ω /
U
Type: Fraction(Polynomial(Integer))
This "twisted dimension " depends on 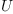 !
!
fricas
d':=
Ω /
X /
U
Type: Fraction(Polynomial(Integer))
(0.0,-1.2)(0.8,-1.2)(0.8,-0.4)
\psbezier[linewidth=0.04](0.8,0.4)(0.8,1.2)(1.6,1.2)(1.6,0.4)
\psline[linewidth=0.04cm](0.0,-0.4)(0.0,0.2)
\psline[linewidth=0.04cm](1.6,-0.4)(1.6,-1.0)
\psline[linewidth=0.04cm](2.8,0.2)(2.8,-1.0)
\psbezier[linewidth=0.04](5.8,-0.4)(5.8,-1.2)(5.0,-1.2)(5.0,-0.4)
\psbezier[linewidth=0.04](5.0,0.4)(5.0,1.2)(4.2,1.2)(4.2,0.4)
\psline[linewidth=0.04cm](5.8,-0.4)(5.8,0.2)
\psline[linewidth=0.04cm](4.2,-0.4)(4.2,-1.0)
\usefont{T1}{ptm}{m}{n}
\rput(2.0948439,-0.095){=}
\usefont{T1}{ptm}{m}{n}
\rput(3.4948437,-0.095){=}
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](4.2,0.4)(4.2,-0.2)(5.0,0.2)(5.0,-0.4)
\psbezier[linewidth=0.04](5.0,0.4)(5.0,-0.2)(4.2,0.2)(4.2,-0.4)
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](0.8,0.4)(0.8,-0.2)(1.6,0.2)(1.6,-0.4)
\psbezier[linewidth=0.04](1.6,0.4)(1.6,-0.2)(0.8,0.2)(0.8,-0.4)
\psline[linewidth=0.04cm](2.8,1.0)(2.8,0.2)
\psline[linewidth=0.04cm](5.8,1.0)(5.8,0.2)
\psline[linewidth=0.04cm](0.0,1.0)(0.0,0.2)
\end{pspicture}
}
\scalebox{1} % Change this value to rescale the drawing.
{
\begin{pspicture}(0,-1.22)(5.82,1.22)
\psbezier[linewidth=0.04](0.0,-0.4)(0.0,-1.2)(0.8,-1.2)(0.8,-0.4)
\psbezier[linewidth=0.04](0.8,0.4)(0.8,1.2)(1.6,1.2)(1.6,0.4)
\psline[linewidth=0.04cm](0.0,-0.4)(0.0,0.2)
\psline[linewidth=0.04cm](1.6,-0.4)(1.6,-1.0)
\psline[linewidth=0.04cm](2.8,0.2)(2.8,-1.0)
\psbezier[linewidth=0.04](5.8,-0.4)(5.8,-1.2)(5.0,-1.2)(5.0,-0.4)
\psbezier[linewidth=0.04](5.0,0.4)(5.0,1.2)(4.2,1.2)(4.2,0.4)
\psline[linewidth=0.04cm](5.8,-0.4)(5.8,0.2)
\psline[linewidth=0.04cm](4.2,-0.4)(4.2,-1.0)
\usefont{T1}{ptm}{m}{n}
\rput(2.0948439,-0.095){=}
\usefont{T1}{ptm}{m}{n}
\rput(3.4948437,-0.095){=}
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](4.2,0.4)(4.2,-0.2)(5.0,0.2)(5.0,-0.4)
\psbezier[linewidth=0.04](5.0,0.4)(5.0,-0.2)(4.2,0.2)(4.2,-0.4)
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](0.8,0.4)(0.8,-0.2)(1.6,0.2)(1.6,-0.4)
\psbezier[linewidth=0.04](1.6,0.4)(1.6,-0.2)(0.8,0.2)(0.8,-0.4)
\psline[linewidth=0.04cm](2.8,1.0)(2.8,0.2)
\psline[linewidth=0.04cm](5.8,1.0)(5.8,0.2)
\psline[linewidth=0.04cm](0.0,1.0)(0.0,0.2)
\end{pspicture}
}](images/2432629302176308249-16.0px.png)
(5.8,-0.9)(5.0,-0.9)(5.0,-0.1)
\psbezier[linewidth=0.04](5.8,-0.1)(5.8,0.7)(5.0,0.7)(5.0,-0.1)
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](4.2,0.7)(4.2,0.1)(5.0,0.5)(5.0,-0.1)
\psbezier[linewidth=0.04](5.0,0.1)(5.0,-0.5)(4.2,-0.1)(4.2,-0.7)
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](0.0,-0.1)(0.0,-0.9)(0.8,-0.9)(0.8,-0.1)
\psbezier[linewidth=0.04](0.0,-0.1)(0.0,0.7)(0.8,0.7)(0.8,-0.1)
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](1.6,0.7)(1.6,0.1)(0.8,0.5)(0.8,-0.1)
\psbezier[linewidth=0.04](0.8,0.1)(0.8,-0.5)(1.6,-0.1)(1.6,-0.7)
\psline[linewidth=0.04cm](2.8,0.3)(2.8,-0.9)
\psline[linewidth=0.04cm](2.8,0.9)(2.8,0.3)
\psline[linewidth=0.04cm](4.2,0.9)(4.2,0.7)
\psline[linewidth=0.04cm](4.2,-0.9)(4.2,-0.7)
\psline[linewidth=0.04cm](1.6,0.9)(1.6,0.7)
\psline[linewidth=0.04cm](1.6,-0.7)(1.6,-0.9)
\usefont{T1}{ptm}{m}{n}
\rput(2.0948439,0.005){=}
\usefont{T1}{ptm}{m}{n}
\rput(3.4948437,0.005){=}
\end{pspicture}
}
\scalebox{1} % Change this value to rescale the drawing.
{
\begin{pspicture}(0,-0.92)(5.82,0.92)
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](5.8,-0.1)(5.8,-0.9)(5.0,-0.9)(5.0,-0.1)
\psbezier[linewidth=0.04](5.8,-0.1)(5.8,0.7)(5.0,0.7)(5.0,-0.1)
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](4.2,0.7)(4.2,0.1)(5.0,0.5)(5.0,-0.1)
\psbezier[linewidth=0.04](5.0,0.1)(5.0,-0.5)(4.2,-0.1)(4.2,-0.7)
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](0.0,-0.1)(0.0,-0.9)(0.8,-0.9)(0.8,-0.1)
\psbezier[linewidth=0.04](0.0,-0.1)(0.0,0.7)(0.8,0.7)(0.8,-0.1)
\psbezier[linewidth=0.04,linestyle=dashed,dash=0.16cm 0.16cm](1.6,0.7)(1.6,0.1)(0.8,0.5)(0.8,-0.1)
\psbezier[linewidth=0.04](0.8,0.1)(0.8,-0.5)(1.6,-0.1)(1.6,-0.7)
\psline[linewidth=0.04cm](2.8,0.3)(2.8,-0.9)
\psline[linewidth=0.04cm](2.8,0.9)(2.8,0.3)
\psline[linewidth=0.04cm](4.2,0.9)(4.2,0.7)
\psline[linewidth=0.04cm](4.2,-0.9)(4.2,-0.7)
\psline[linewidth=0.04cm](1.6,0.9)(1.6,0.7)
\psline[linewidth=0.04cm](1.6,-0.7)(1.6,-0.9)
\usefont{T1}{ptm}{m}{n}
\rput(2.0948439,0.005){=}
\usefont{T1}{ptm}{m}{n}
\rput(3.4948437,0.005){=}
\end{pspicture}
}](images/2886468678326544459-16.0px.png)