Edit detail for Sqrt3Demo revision 4 of 4
| 1 2 3 4 | ||
|
Editor: hemmecke
Time: 2008/08/16 06:58:42 GMT-7 |
||
| Note: | ||
changed: -Alternatively, we could also use Renaud Rioboo's 'RECLOS package, which has both mathematical equality and ordering. Unfortunately, it is not as easy to use - most importantly, you have to "name" your real roots, if you want simple answers: Alternatively, we could also use Renaud Rioboo's 'RECLOS' package, which has both mathematical equality and ordering. Unfortunately, it is not as easy to use - most importantly, you have to "name" your real roots, if you want simple answers: changed: -'AlgebraicNumber' doesn't like the following: AlgebraicNumber doesn't like the following: changed: -f25 := sqrt(1/25,5)$RAN; f25 := sqrt(1/25,5)$RAN changed: -sqrt(f32-f27,3)-f25*(1+f3-f3^2) expr1 := sqrt(f32-f27,3) expr2 := (1+f3-f3^2) expr1 - f25*expr2 changed: -Although the main point of 'RECLOS' is supposed do be mathematical ordering and approximation, I could not find a convincing exmaple. From the 'examples' section of 'RECLOS': Although the main point of 'RECLOS' is supposed do be mathematical ordering and approximation, I could not find a convincing example. From the "examples" section of 'RECLOS':
Some demo involving the algebraic number ![]() .
.
fricas
(1) -> t1 := (sqrt(3)-3)*(sqrt(3)+1)/6
| (1) |
Type: AlgebraicNumber?
fricas
tt1 := -1/sqrt(3)
| (2) |
Type: AlgebraicNumber?
fricas
t2 := sqrt(3)/6
| (3) |
Type: AlgebraicNumber?
fricas
t1+t2
| (4) |
Type: AlgebraicNumber?
fricas
tt1+t2
| (5) |
Type: AlgebraicNumber?
Note that in PanAxiom the above are not generic expressions but of type AlgebraicNumber?.
Alternatively, we could also use Renaud Rioboo's RECLOS package,
which has both mathematical equality and ordering.
Unfortunately, it is not as easy to use - most importantly,
you have to "name" your real roots, if you want simple answers:
fricas
RAN ==> RECLOS FRAC INT
Type: Void
fricas
x1 := (sqrt(3)$RAN-3)*(sqrt(3)$RAN+1)/6
| (6) |
Type: RealClosure(Fraction(Integer))
fricas
xx1 := -1/sqrt(3)$RAN
| (7) |
Type: RealClosure(Fraction(Integer))
fricas
(x1=xx1)@Boolean
| (8) |
Type: Boolean
It's preferable to give names to the roots:
fricas
s3 := sqrt(3)$RAN
| (9) |
Type: RealClosure(Fraction(Integer))
fricas
(s3-3)*(s3+1)/6
| (10) |
Type: RealClosure(Fraction(Integer))
AlgebraicNumber? doesn't like the following:
fricas
f3 := sqrt(3,5)$RAN
| (11) |
Type: RealClosure(Fraction(Integer))
fricas
f25 := sqrt(1/25,5)$RAN
| (12) |
Type: RealClosure(Fraction(Integer))
fricas
f32 := sqrt(32/5,5)$RAN;
Type: RealClosure(Fraction(Integer))
fricas
f27 := sqrt(27/5,5)$RAN;
Type: RealClosure(Fraction(Integer))
fricas
expr1 := sqrt(f32-f27,3)
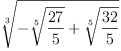 | (13) |
Type: RealClosure(Fraction(Integer))
fricas
expr2 := (1+f3-f3^2)
| (14) |
Type: RealClosure(Fraction(Integer))
fricas
expr1 - f25*expr2
| (15) |
Type: RealClosure(Fraction(Integer))
Although the main point of RECLOS is supposed do be mathematical
ordering and approximation, I could not find a convincing example.
From the "examples" section of 'RECLOS':
fricas
s := sqrt(190)$RAN+sqrt(1751)$RAN-sqrt(208)$RAN-sqrt(1698)$RAN
| (16) |
Type: RealClosure(Fraction(Integer))
fricas
approximate(s,10^-15)::Float
| (17) |
Type: Float
But we get the same without 'RECLOS':
fricas
t := sqrt(190)+sqrt(1751)-sqrt(208)-sqrt(1698)
| (18) |
Type: AlgebraicNumber?
fricas
digits(30);
Type: PositiveInteger?
fricas
numeric t - approximate(s,10^-30)::Float
| (19) |
Type: Float