fricas
(1) -> )abbrev domain CMAP CellMap
++
CellMap(R,n) : Exports == Implementation where
R: Join(Ring,Comparable)
n: NonNegativeInteger
X ==> Expression R
DP ==> DirectProduct
OF ==> OutputForm
NNI ==> NonNegativeInteger
MAP ==> List X -> List X
DOM ==> List(Segment X)
Exports == Join(CoercibleTo OF,SetCategory,Evalable X) with
_= : (%,%) -> Boolean
++ f1=f2 checks if two given cell maps are equal, that is if they have
++ the same domain D and the same mapping from D into X^n.
cellMap : (DOM,MAP) -> %
++ cellMap(D,f) is the constructor. Usually one has to specify the
++ dimension of the target space. For example, let Q=[a..b,c..d], then
++ cellMap(Q,Z+->[sin(Z.1),cos(Z.2),Z.1*Z.2])$CMAP(INT,3) defines a
++ 2-surface in X^3.
getDom : % -> DOM
++ getDom(f) extracts the domain of f.
getMap : % -> MAP
++ getMap(f) extracts the map of f.
faces : % -> List List(%)
++ faces(f) returns the faces of f, that means the images of the boundary
++ of the domain. Note: the returned list contains pairs of faces
++ corresponding to the endpoints of intervals.
coords : (Symbol,PositiveInteger) -> List X
++ coords(s,m) provides a sample of coordinates s[1],..,s[m] as a list.
coordSymbols : (Symbol,PositiveInteger) -> List Symbol
++ coordSymbols(s,m) provides a sample of coordinates s[1],..,s[m] as a
++ list of symbols.
jacobianMatrix : % -> (List X -> Matrix X)
++ jacobianMatrix(f) returns the Jacobian matrix as a marix valued
++ function defined on the same cell as the cellMap.
tangentSpace : % -> (List(X) -> List(Vector X))
++ tangentSpace(f) returns a
coerce : % -> OutputForm
++ coerce(f) gives the output representation.
Implementation == add
Rep := Record(d:DOM,f:MAP)
(x:% = y:%):Boolean ==
l:NNI:=min(#(x.d),#(y.d))
v:List X
for j in 1..l repeat
s:X:=subscript('z,[j::OF])::X
v:=concat(v,s::X)
x.d =y.d and (x.f) v = (y.f) v => true
false
cellMap(dd:DOM,ff:MAP):% ==
#dd > n => error concat("#DOM > ",string n)
v:List X:=[1::X for j in 1..#dd]
~test(#ff(v)=n) => error concat("#Range ~= ", string n)
construct(dd,ff)
faceLoHi(x:%,i:NNI,lo:Boolean):% ==
l:NNI:=#(x.d)
v:List X
for j in 1..l repeat
if j=i then
if lo then
s : X := low((x.d)(i))
else
s: X := high((x.d)(i))
else
if j>i then
s:X:=subscript('%,[(j-1)::OF])::X
else
s:X:=subscript('%,[j::OF])::X
v:=concat(v,s::X)
vv:=delete(v,i..i)
dd:List(Segment X):=delete(x.d,i..i)
ff:MAP:=vv+->(x.f) v
cellMap(dd,ff)
faces(x:%):List List(%) ==
l:NNI:=#(x.d)
[[faceLoHi(x,j,true), faceLoHi(x,j,false)] for j in 1..l]
getDom(x) == x.d
getMap(x) == x.f
coordSymbols(s:Symbol,m:PositiveInteger):List Symbol ==
[subscript(s,[j::OF]) for j in 1..m]
coords(s:Symbol,m:PositiveInteger):List X ==
xs:=[subscript(s,[j::OF]) for j in 1..m]
[coerce(xs.j)$X for j in 1..#xs]
jacobianMatrix(S:%):List(X) -> Matrix(X) ==
--xs:List Symbol:=v:=[subscript('x,[j::OF]) for j in 1..#(getDom S)]
--x:List X:=[coerce(xs.j)$X for j in 1..#xs]
xs:List Symbol:=coordSymbols('x,#(getDom S)::PositiveInteger)
x:List X:=coords('x,#xs::PositiveInteger)
F:List X:=(getMap S) x
J:Matrix(X):=matrix [[D(ff,u) for u in xs] for ff in F]
if Matrix(X) has Join(SetCategory,Evalable(X)) then
(y:List X):Matrix(X)+-> eval(J,x,y)
else
(y:List X):Matrix(X)+-> J
tangentSpace(S:%):List(X) -> List(Vector X) ==
J:=jacobianMatrix(S)
x:List X:=coords('x,#(getDom S)::PositiveInteger)
if Vector(X) has Join(SetCategory,Evalable(X)) then
if X has EuclideanDomain then
cs:List(Vector X):=columnSpace(J x)
(y:List X):List Vector(X)+-> [eval(t,x,y) for t in cs]
coerce(x) ==
v:List X
for j in 1..#(x.d) repeat
s:X:=subscript('%,[j::OF])::X
v:=concat(v,s::X)
r:List X:=(x.f) v
hconcat [message("|"), x.d::OF, message(" -> "), r::OF, message("|")]
fricas
)abbrev domain SCMPLX SurfaceComplex
++
SurfaceComplex(R,n) : Exports == Implementation where
NNI ==> NonNegativeInteger
INT ==> Integer
n : NNI
R : Join(Ring,Comparable)
CMAP ==> CellMap(R,n)
CTOF ==> CoercibleTo OutputForm
X ==> Expression R
OF ==> OutputForm
MAP ==> List X -> List X
DOM ==> List(Segment X)
Exports == Join(AbelianGroup ,CTOF, RetractableTo CMAP) with
bdry : % -> %
++ bdry(S) computes the boundary of the surface complex S.
size : % -> NNI
++ size(S) returns the number of "pieces" of the surface complex S.
nthCoef : (%,Integer) -> Integer
++ nthCoef(x, n) returns the coefficient of the n^th term of x.
nthFactor : (%,Integer) -> CMAP
++ nthFactor(x, n) returns the factor of the n^th term of x.
zero? : % -> Boolean
++ zero?(S) returns true if S is the empty surface complex.
_= : (%,%) -> Boolean
++ S=S' checks if the surface complexes S and S' are equal.
terms : % -> List(Record(gen: CMAP,exp: Integer))
++ terms(S) returns all terms of S as a record.
mapGen : ((CMAP -> CMAP),%) -> %
++ mapGen(f, e1 a1 +...+ en an) returns
++ \spad{e1 f(a1) +...+ en f(an)}.
mapCoef : ((Integer -> Integer),%) -> %
++ mapCoef(f, e1 a1 +...+ en an) returns
++ \spad{f(e1) a1 +...+ f(en) an}.
construct : (DOM,MAP) -> %
++ construct(d,f) constructs a term (piece) of a k-surface, where
++ d is the domain (a k-cell) and f is a mapping from d to a vector
++ space of dimension n.
--coerce : % -> OutputForm
Implementation == FreeModule(Integer, CMAP) add
Rep:=FreeModule(Integer, CMAP)
bdry(c:%):% ==
if size(c) = 1 then
s:=nthFactor(c,1)
l:=faces(s)
fs:=[(a.2::Rep-a.1::Rep) for a in l]
sgn:=(j:INT):INT+->if even? (j-1) then 1 else -1
nthCoef(c,1)*reduce("+",[sgn(j)*fs.j::Rep for j in 1..#fs])
else
ct:=[(nthCoef(c,j)*nthFactor(c,j))::Rep for j in 1..size(c)]
reduce("+",map(bdry,ct))
construct(d:DOM,f:MAP):% == cellMap(d,f)$CMAP::%
fricas
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/9034321958150369551-25px.001.spad
using old system compiler.
CMAP abbreviates domain CellMap
------------------------------------------------------------------------
initializing NRLIB CMAP for CellMap
compiling into NRLIB CMAP
****** Domain: R already in scope
compiling exported = : (%,%) -> Boolean
Time: 0.04 SEC.
compiling exported cellMap : (List Segment Expression R,List Expression R -> List Expression R) -> %
Time: 0 SEC.
compiling local faceLoHi : (%,NonNegativeInteger,Boolean) -> %
Time: 0.01 SEC.
compiling exported faces : % -> List List %
Time: 0 SEC.
compiling exported getDom : % -> List Segment Expression R
CMAP;getDom;%L;5 is replaced by QCAR
Time: 0 SEC.
compiling exported getMap : % -> List Expression R -> List Expression R
CMAP;getMap;%M;6 is replaced by QCDR
Time: 0 SEC.
compiling exported coordSymbols : (Symbol,PositiveInteger) -> List Symbol
Time: 0 SEC.
compiling exported coords : (Symbol,PositiveInteger) -> List Expression R
Time: 0.02 SEC.
compiling exported jacobianMatrix : % -> List Expression R -> Matrix Expression R
****** Domain: (Matrix (Expression R)) already in scope
augmenting (Matrix (Expression R)): (Evalable (Expression R))
Time: 0.02 SEC.
compiling exported tangentSpace : % -> List Expression R -> List Vector Expression R
****** Domain: (Vector (Expression R)) already in scope
augmenting (Vector (Expression R)): (Evalable (Expression R))
****** Domain: (Expression R) already in scope
augmenting (Expression R): (EuclideanDomain)
Time: 0.04 SEC.
compiling exported coerce : % -> OutputForm
Time: 0 SEC.
(time taken in buildFunctor: 0)
;;; *** |CellMap| REDEFINED
;;; *** |CellMap| REDEFINED
Time: 0 SEC.
Warnings:
[1] =: d has no value
[2] =: v has no value
[3] =: f has no value
[4] faceLoHi: d has no value
[5] faceLoHi: v has no value
[6] faceLoHi: f has no value
[7] faces: d has no value
[8] getDom: d has no value
[9] getMap: f has no value
[10] coerce: d has no value
[11] coerce: v has no value
[12] coerce: f has no value
Cumulative Statistics for Constructor CellMap
Time: 0.16 seconds
finalizing NRLIB CMAP
Processing CellMap for Browser database:
--------constructor---------
--------(= ((Boolean) % %))---------
--------(cellMap (% (List (Segment (Expression R))) (Mapping (List (Expression R)) (List (Expression R)))))---------
--------(getDom ((List (Segment (Expression R))) %))---------
--------(getMap ((Mapping (List (Expression R)) (List (Expression R))) %))---------
--------(faces ((List (List %)) %))---------
--------(coords ((List (Expression R)) (Symbol) (PositiveInteger)))---------
--------(coordSymbols ((List (Symbol)) (Symbol) (PositiveInteger)))---------
--------(jacobianMatrix ((Mapping (Matrix (Expression R)) (List (Expression R))) %))---------
--------(tangentSpace ((Mapping (List (Vector (Expression R))) (List (Expression R))) %))---------
--------(coerce ((OutputForm) %))---------
; compiling file "/var/aw/var/LatexWiki/CMAP.NRLIB/CMAP.lsp" (written 15 MAR 2025 09:54:09 AM):
; wrote /var/aw/var/LatexWiki/CMAP.NRLIB/CMAP.fasl
; compilation finished in 0:00:00.040
------------------------------------------------------------------------
CellMap is now explicitly exposed in frame initial
CellMap will be automatically loaded when needed from
/var/aw/var/LatexWiki/CMAP.NRLIB/CMAP
SCMPLX abbreviates domain SurfaceComplex
------------------------------------------------------------------------
initializing NRLIB SCMPLX for SurfaceComplex
compiling into NRLIB SCMPLX
****** Domain: R already in scope
Local variable Rep type redefined: (Join (BiModule (Integer) (Integer)) (FreeModuleCategory (Integer) (CellMap R n)) (CATEGORY domain (IF (has (Integer) (CommutativeRing)) (ATTRIBUTE (Module (Integer))) noBranch) (IF (has (Integer) (SemiRing)) (ATTRIBUTE (RetractableTo (CellMap R n))) noBranch) (IF (has (Integer) (Hashable)) (IF (has (CellMap R n) (Hashable)) (ATTRIBUTE (Hashable)) noBranch) noBranch) (IF (has (CellMap R n) (OrderedSet)) (PROGN (IF (has (Integer) (OrderedAbelianMonoid)) (ATTRIBUTE (OrderedAbelianMonoid)) noBranch) (IF (has (Integer) (OrderedAbelianMonoidSup)) (ATTRIBUTE (OrderedAbelianMonoidSup)) noBranch)) noBranch) (SIGNATURE * (% (Integer) (CellMap R n))) (SIGNATURE * (% (CellMap R n) (Integer))))) to (Join (SetCategory) (CATEGORY domain (SIGNATURE construct ((Record (: d (List (Segment (Expression R)))) (: f (Mapping (List (Expression R)) (List (Expression R))))) (List (Segment (Expression R))) (Mapping (List (Expression R)) (List (Expression R))))) (SIGNATURE ~= ((Boolean) (Record (: d (List (Segment (Expression R)))) (: f (Mapping (List (Expression R)) (List (Expression R))))) (Record (: d (List (Segment (Expression R)))) (: f (Mapping (List (Expression R)) (List (Expression R))))))) (SIGNATURE coerce ((OutputForm) (Record (: d (List (Segment (Expression R)))) (: f (Mapping (List (Expression R)) (List (Expression R))))))) (SIGNATURE elt ((List (Segment (Expression R))) (Record (: d (List (Segment (Expression R)))) (: f (Mapping (List (Expression R)) (List (Expression R))))) d)) (SIGNATURE elt ((Mapping (List (Expression R)) (List (Expression R))) (Record (: d (List (Segment (Expression R)))) (: f (Mapping (List (Expression R)) (List (Expression R))))) f)) (SIGNATURE setelt! ((List (Segment (Expression R))) (Record (: d (List (Segment (Expression R)))) (: f (Mapping (List (Expression R)) (List (Expression R))))) d (List (Segment (Expression R))))) (SIGNATURE setelt! ((Mapping (List (Expression R)) (List (Expression R))) (Record (: d (List (Segment (Expression R)))) (: f (Mapping (List (Expression R)) (List (Expression R))))) f (Mapping (List (Expression R)) (List (Expression R))))) (SIGNATURE copy ((Record (: d (List (Segment (Expression R)))) (: f (Mapping (List (Expression R)) (List (Expression R))))) (Record (: d (List (Segment (Expression R)))) (: f (Mapping (List (Expression R)) (List (Expression R)))))))))
compiling exported bdry : % -> %
Time: 0.02 SEC.
compiling exported construct : (List Segment Expression R,List Expression R -> List Expression R) -> %
Time: 0 SEC.
(time taken in buildFunctor: 0)
;;; *** |SurfaceComplex| REDEFINED
;;; *** |SurfaceComplex| REDEFINED
Time: 0 SEC.
Cumulative Statistics for Constructor SurfaceComplex
Time: 0.03 seconds
--------------non extending category----------------------
.. SurfaceComplex(#1,#2) of cat
(|Join| (|AbelianGroup|) (|CoercibleTo| (|OutputForm|))
(|RetractableTo| (|CellMap| |#1| |#2|))
(CATEGORY |domain| (SIGNATURE |bdry| (% %))
(SIGNATURE |size| ((|NonNegativeInteger|) %))
(SIGNATURE |nthCoef| ((|Integer|) % (|Integer|)))
(SIGNATURE |nthFactor| ((|CellMap| |#1| |#2|) % (|Integer|)))
(SIGNATURE |zero?| ((|Boolean|) %)) (SIGNATURE = ((|Boolean|) % %))
(SIGNATURE |terms|
((|List|
(|Record| (|:| |gen| (|CellMap| |#1| |#2|))
(|:| |exp| (|Integer|))))
%))
(SIGNATURE |mapGen|
(% (|Mapping| (|CellMap| |#1| |#2|) (|CellMap| |#1| |#2|)) %))
(SIGNATURE |mapCoef| (% (|Mapping| (|Integer|) (|Integer|)) %))
(SIGNATURE |construct|
(% (|List| (|Segment| (|Expression| |#1|)))
(|Mapping| (|List| (|Expression| |#1|))
(|List| (|Expression| |#1|))))))) has no
(|BiModule| (|Integer|) (|Integer|)) finalizing NRLIB SCMPLX
Processing SurfaceComplex for Browser database:
--------constructor---------
--------(bdry (% %))---------
--------(size ((NonNegativeInteger) %))---------
--------(nthCoef ((Integer) % (Integer)))---------
--------(nthFactor ((CellMap R n) % (Integer)))---------
--------(zero? ((Boolean) %))---------
--------(= ((Boolean) % %))---------
--------(terms ((List (Record (: gen (CellMap R n)) (: exp (Integer)))) %))---------
--------(mapGen (% (Mapping (CellMap R n) (CellMap R n)) %))---------
--------(mapCoef (% (Mapping (Integer) (Integer)) %))---------
--------(construct (% (List (Segment (Expression R))) (Mapping (List (Expression R)) (List (Expression R)))))---------
; compiling file "/var/aw/var/LatexWiki/SCMPLX.NRLIB/SCMPLX.lsp" (written 15 MAR 2025 09:54:09 AM):
; wrote /var/aw/var/LatexWiki/SCMPLX.NRLIB/SCMPLX.fasl
; compilation finished in 0:00:00.012
------------------------------------------------------------------------
SurfaceComplex is now explicitly exposed in frame initial
SurfaceComplex will be automatically loaded when needed from
/var/aw/var/LatexWiki/SCMPLX.NRLIB/SCMPLXfricas
)clear all
All user variables and function definitions have been cleared.
R ==> EXPR INT
Type: Void
fricas
OF ==> OutputForm
Type: Void
fricas
-- Cell map
R2 ==> CellMap(INT,2)
Type: Void
fricas
R3 ==> CellMap(INT,3)
Type: Void
fricas
R4 ==> CellMap(INT,4)
Type: Void
fricas
Q2 ==> [0..1,0..1::R]
Type: Void
fricas
Q3 ==> concat(Q2,[0..1::R])
Type: Void
fricas
--xs:List Symbol:=coordSymbols('x,4)$R4
----------------------------------------------------------------
-- https://en.wikipedia.org/wiki/Jacobian_matrix_and_determinant
----------------------------------------------------------------
-- Example 1
F1:=cellMap(Q2,X+->[X.1^2*X.2,5*X.1+sin(X.2)])$R2
Type: CellMap
?(Integer,
2)
fricas
J:=jacobianMatrix(F1)
Type: (List(Expression(Integer)) -> Matrix(Expression(Integer)))
fricas
x:=coords('x,2)$R2
Type: List(Expression(Integer))
fricas
J x
Type: Matrix(Expression(Integer))
fricas
determinant(J x)
Type: Expression(Integer)
fricas
test(J x = matrix [[2*x.1*x.2,x.1^2],[5,cos(x.2)]])
Type: Boolean
fricas
test(determinant(J x) = 2*x.1*x.2*cos(x.2)-5*x.1^2)
Type: Boolean
fricas
-- Example 2
F2:=cellMap(Q2,X+->[X.1*cos(X.2),X.1*sin(X.2)])$R2
Type: CellMap
?(Integer,
2)
fricas
J:=jacobianMatrix(F2)
Type: (List(Expression(Integer)) -> Matrix(Expression(Integer)))
fricas
x:=[r::R,phi::R]
Type: List(Expression(Integer))
fricas
(getMap F2) x
Type: List(Expression(Integer))
fricas
J x
Type: Matrix(Expression(Integer))
fricas
determinant(J x)
Type: Expression(Integer)
fricas
test( J x = matrix [[cos(x.2),-x.1*sin(x.2)],[sin(x.2),x.1*cos(x.2)]])
Type: Boolean
fricas
test( normalize determinant(J x) = x.1)
Type: Boolean
fricas
-- Example 3
F3:=cellMap(Q3,Z+->[Z.1*sin(Z.2)*cos(Z.3),Z.1*sin(Z.2)*sin(Z.3),Z.1*cos(Z.2)])$R3
Type: CellMap
?(Integer,
3)
fricas
J:=jacobianMatrix(F3)
Type: (List(Expression(Integer)) -> Matrix(Expression(Integer)))
fricas
z:=[r::R,th::R,phi::R]
Type: List(Expression(Integer))
fricas
(getMap F3) z
Type: List(Expression(Integer))
fricas
J z
Type: Matrix(Expression(Integer))
fricas
determinant(J z)
Type: Expression(Integer)
fricas
M:=[[sin(z.2)*cos(z.3),z.1*cos(z.2)*cos(z.3),-z.1*sin(z.2)*sin(z.3)],_
[sin(z.2)*sin(z.3),z.1*cos(z.2)*sin(z.3),z.1*sin(z.2)*cos(z.3)],_
[cos(z.2),-z.1*sin(z.2),0]]
Type: List(List(Expression(Integer)))
fricas
test( J z = matrix M)
Type: Boolean
fricas
test( simplify determinant(J z) = z.1^2*sin(z.2) )
Type: Boolean
fricas
-- Example 4
F4:=cellMap(Q3,X+->[X.1,5*X.3,4*X.2^2-2*X.3,X.3*sin(X.1)])$R4
Type: CellMap
?(Integer,
4)
fricas
J:=jacobianMatrix(F4)
Type: (List(Expression(Integer)) -> Matrix(Expression(Integer)))
fricas
x:=coords('x,4)$R4
Type: List(Expression(Integer))
fricas
J x
Type: Matrix(Expression(Integer))
fricas
nullSpace (J x)
Type: List(Vector(Expression(Integer)))
fricas
rank (J x)
fricas
T:=tangentSpace(F4)$R4
Type: (List(Expression(Integer)) -> List(Vector(Expression(Integer))))
fricas
T x
Type: List(Vector(Expression(Integer)))
fricas
test(J x = matrix [[1,0,0],[0,0,5],[0,8*x.2,-2],[x.3*cos(x.1),0,sin(x.1)]])
Type: Boolean
fricas
test( rank (J x) = 3)
Type: Boolean
fricas
test( J x = transpose matrix (T x))
Type: Boolean
fricas
-- Example 5
F5:=cellMap(Q3,X+->[5*X.2,4*X.1^2-2*sin(X.2*X.3),X.2*X.3])$R3
Type: CellMap
?(Integer,
3)
fricas
J:=jacobianMatrix(F5)
Type: (List(Expression(Integer)) -> Matrix(Expression(Integer)))
fricas
x:=coords('x,3)$R3
Type: List(Expression(Integer))
fricas
J x
Type: Matrix(Expression(Integer))
fricas
determinant (J x)
Type: Expression(Integer)
fricas
M:=[[0,5,0],[8*x.1,-2*x.3*cos(x.2*x.3),-2*x.2*cos(x.2*x.3)],[0,x.3,x.2]]
Type: List(List(Expression(Integer)))
fricas
T:=tangentSpace(F5)$R3
Type: (List(Expression(Integer)) -> List(Vector(Expression(Integer))))
fricas
test(J x = matrix M)
Type: Boolean
fricas
test(determinant (J x) = -40*x.1*x.2)
Type: Boolean
fricas
test( J x = transpose matrix (T x))
Type: Boolean

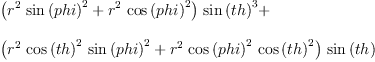
![\label{eq22}\begin{array}{@{}l}
\displaystyle
\left[{\left[{{\cos \left({phi}\right)}\ {\sin \left({th}\right)}}, \:{r \ {\cos \left({phi}\right)}\ {\cos \left({th}\right)}}, \: -{r \ {\sin \left({phi}\right)}\ {\sin \left({th}\right)}}\right]}, \: \right.
\
\
\displaystyle
\left.{\left[{{\sin \left({phi}\right)}\ {\sin \left({th}\right)}}, \:{r \ {\cos \left({th}\right)}\ {\sin \left({phi}\right)}}, \:{r \ {\cos \left({phi}\right)}\ {\sin \left({th}\right)}}\right]}, \: \right.
\
\
\displaystyle
\left.{\left[{\cos \left({th}\right)}, \: -{r \ {\sin \left({th}\right)}}, \: 0 \right]}\right]
\label{eq22}\begin{array}{@{}l}
\displaystyle
\left[{\left[{{\cos \left({phi}\right)}\ {\sin \left({th}\right)}}, \:{r \ {\cos \left({phi}\right)}\ {\cos \left({th}\right)}}, \: -{r \ {\sin \left({phi}\right)}\ {\sin \left({th}\right)}}\right]}, \: \right.
\
\
\displaystyle
\left.{\left[{{\sin \left({phi}\right)}\ {\sin \left({th}\right)}}, \:{r \ {\cos \left({th}\right)}\ {\sin \left({phi}\right)}}, \:{r \ {\cos \left({phi}\right)}\ {\sin \left({th}\right)}}\right]}, \: \right.
\
\
\displaystyle
\left.{\left[{\cos \left({th}\right)}, \: -{r \ {\sin \left({th}\right)}}, \: 0 \right]}\right]](images/5318105449462755905-16.0px.png)
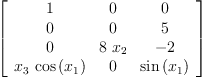
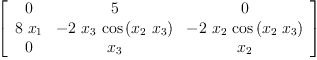
![\label{eq41}\begin{array}{@{}l}
\displaystyle
\left[{\left[ 0, \: 5, \: 0 \right]}, \:{\left[{8 \ {x_{1}}}, \: -{2 \ {x_{3}}\ {\cos \left({{x_{2}}\ {x_{3}}}\right)}}, \: -{2 \ {x_{2}}\ {\cos \left({{x_{2}}\ {x_{3}}}\right)}}\right]}, \: \right.
\
\
\displaystyle
\left.{\left[ 0, \:{x_{3}}, \:{x_{2}}\right]}\right]
\label{eq41}\begin{array}{@{}l}
\displaystyle
\left[{\left[ 0, \: 5, \: 0 \right]}, \:{\left[{8 \ {x_{1}}}, \: -{2 \ {x_{3}}\ {\cos \left({{x_{2}}\ {x_{3}}}\right)}}, \: -{2 \ {x_{2}}\ {\cos \left({{x_{2}}\ {x_{3}}}\right)}}\right]}, \: \right.
\
\
\displaystyle
\left.{\left[ 0, \:{x_{3}}, \:{x_{2}}\right]}\right]](images/4541965723086106071-16.0px.png)