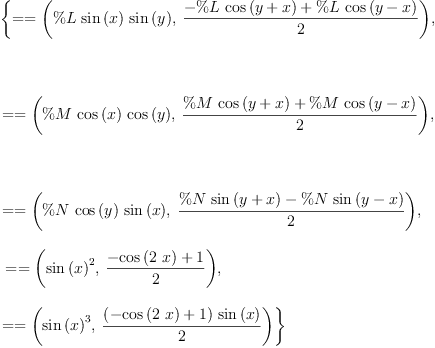Demonstration of modifying and testing a SPAD file

I changed the abbreviation to TRMANIP2 and the name to TranscendentalManipulations2 so I can call both the old and new package if necessary.

(1) -> <spad>

)abbrev package TRMANIP2 TranscendentalManipulations2
++ Transformations on transcendental objects
++ Author: Bob Sutor, Manuel Bronstein
++ Date Created: Way back
++ Date Last Updated: 22 January 1996, added simplifyLog MCD.
++ Description:
++   TranscendentalManipulations provides functions to simplify and
++   expand expressions involving transcendental operators.
++ Keywords: transcendental, manipulation.
TranscendentalManipulations2(R, F): Exports == Implementation where
  R : Join(OrderedSet, GcdDomain)
  F : Join(FunctionSpace R, TranscendentalFunctionCategory)

  Z       ==> Integer
  K       ==> Kernel F
  P       ==> SparseMultivariatePolynomial(R, K)
  UP      ==> SparseUnivariatePolynomial P
  POWER   ==> "%power"::Symbol
  POW     ==> Record(val: F,exponent: Z)
  PRODUCT ==> Record(coef : Z, var : K)
  FPR     ==> Fraction Polynomial R

  Exports ==> with
    expand     : F -> F
      ++ expand(f) performs the following expansions on f:\begin{items}
      ++ \item 1. logs of products are expanded into sums of logs,
      ++ \item 2. trigonometric and hyperbolic trigonometric functions
      ++ of sums are expanded into sums of products of trigonometric
      ++ and hyperbolic trigonometric functions.
      ++ \item 3. formal powers of the form \spad{(a/b)^c} are expanded into
      ++ \spad{a^c * b^(-c)}.
      ++ \end{items}
    simplify   : F -> F
      ++ simplify(f) performs the following simplifications on f:\begin{items}
      ++ \item 1. rewrites trigs and hyperbolic trigs in terms
      ++ of \spad{sin} ,\spad{cos}, \spad{sinh}, \spad{cosh}.
      ++ \item 2. rewrites \spad{sin^2} and \spad{sinh^2} in terms
      ++ of \spad{cos} and \spad{cosh},
      ++ \item 3. rewrites \spad{exp(a)*exp(b)} as \spad{exp(a+b)}.
      ++ \item 4. rewrites \spad{(a^(1/n))^m * (a^(1/s))^t} as a single
      ++ power of a single radical of \spad{a}.
      ++ \end{items}
    htrigs     : F -> F
      ++ htrigs(f) converts all the exponentials in f into
      ++ hyperbolic sines and cosines.
    simplifyExp: F -> F
      ++ simplifyExp(f) converts every product \spad{exp(a)*exp(b)}
      ++ appearing in f into \spad{exp(a+b)}.
    simplifyLog : F -> F
      ++ simplifyLog(f) converts every \spad{log(a) - log(b)} appearing in f
      ++ into \spad{log(a/b)}, every \spad{log(a) + log(b)} into \spad{log(a*b)}
      ++ and every \spad{n*log(a)} into \spad{log(a^n)}.
    expandPower: F -> F
      ++ expandPower(f) converts every power \spad{(a/b)^c} appearing
      ++ in f into \spad{a^c * b^(-c)}.
    expandLog  : F -> F
      ++ expandLog(f) converts every \spad{log(a/b)} appearing in f into
      ++ \spad{log(a) - log(b)}, and every \spad{log(a*b)} into
      ++ \spad{log(a) + log(b)}..
    cos2sec    : F -> F
      ++ cos2sec(f) converts every \spad{cos(u)} appearing in f into
      ++ \spad{1/sec(u)}.
    cosh2sech  : F -> F
      ++ cosh2sech(f) converts every \spad{cosh(u)} appearing in f into
      ++ \spad{1/sech(u)}.
    cot2trig   : F -> F
      ++ cot2trig(f) converts every \spad{cot(u)} appearing in f into
      ++ \spad{cos(u)/sin(u)}.
    coth2trigh : F -> F
      ++ coth2trigh(f) converts every \spad{coth(u)} appearing in f into
      ++ \spad{cosh(u)/sinh(u)}.
    csc2sin    : F -> F
      ++ csc2sin(f) converts every \spad{csc(u)} appearing in f into
      ++ \spad{1/sin(u)}.
    csch2sinh  : F -> F
      ++ csch2sinh(f) converts every \spad{csch(u)} appearing in f into
      ++ \spad{1/sinh(u)}.
    sec2cos    : F -> F
      ++ sec2cos(f) converts every \spad{sec(u)} appearing in f into
      ++ \spad{1/cos(u)}.
    sech2cosh  : F -> F
      ++ sech2cosh(f) converts every \spad{sech(u)} appearing in f into
      ++ \spad{1/cosh(u)}.
    sin2csc    : F -> F
      ++ sin2csc(f) converts every \spad{sin(u)} appearing in f into
      ++ \spad{1/csc(u)}.
    sinh2csch  : F -> F
      ++ sinh2csch(f) converts every \spad{sinh(u)} appearing in f into
      ++ \spad{1/csch(u)}.
    tan2trig   : F -> F
      ++ tan2trig(f) converts every \spad{tan(u)} appearing in f into
      ++ \spad{sin(u)/cos(u)}.
    tanh2trigh : F -> F
      ++ tanh2trigh(f) converts every \spad{tanh(u)} appearing in f into
      ++ \spad{sinh(u)/cosh(u)}.
    tan2cot    : F -> F
      ++ tan2cot(f) converts every \spad{tan(u)} appearing in f into
      ++ \spad{1/cot(u)}.
    tanh2coth  : F -> F
      ++ tanh2coth(f) converts every \spad{tanh(u)} appearing in f into
      ++ \spad{1/coth(u)}.
    cot2tan    : F -> F
      ++ cot2tan(f) converts every \spad{cot(u)} appearing in f into
      ++ \spad{1/tan(u)}.
    coth2tanh  : F -> F
      ++ coth2tanh(f) converts every \spad{coth(u)} appearing in f into
      ++ \spad{1/tanh(u)}.
    removeCosSq: F -> F
      ++ removeCosSq(f) converts every \spad{cos(u)^2} appearing in f into
      ++ \spad{1 - sin(x)^2}, and also reduces higher
      ++ powers of \spad{cos(u)} with that formula.
    removeSinSq: F -> F
      ++ removeSinSq(f) converts every \spad{sin(u)^2} appearing in f into
      ++ \spad{1 - cos(x)^2}, and also reduces higher powers of
      ++ \spad{sin(u)} with that formula.
    removeCoshSq:F -> F
      ++ removeCoshSq(f) converts every \spad{cosh(u)^2} appearing in f into
      ++ \spad{1 - sinh(x)^2}, and also reduces higher powers of
      ++ \spad{cosh(u)} with that formula.
    removeSinhSq:F -> F
      ++ removeSinhSq(f) converts every \spad{sinh(u)^2} appearing in f into
      ++ \spad{1 - cosh(x)^2}, and also reduces higher powers
      ++ of \spad{sinh(u)} with that formula.
    if R has PatternMatchable(R) and R has ConvertibleTo(Pattern(R)) and F has ConvertibleTo(Pattern(R)) and F has PatternMatchable R then
      expandTrigProducts : F -> F
        ++ expandTrigProducts(e) replaces \axiom{sin(x)*sin(y)} by
        ++ \spad{(cos(x-y)-cos(x+y))/2}, \axiom{cos(x)*cos(y)} by
        ++ \spad{(cos(x-y)+cos(x+y))/2}, and \axiom{sin(x)*cos(y)} by
        ++ \spad{(sin(x-y)+sin(x+y))/2}.  Note that this operation uses
        ++ the pattern matcher and so is relatively expensive.  To avoid
        ++ getting into an infinite loop the transformations are applied
        ++ at most ten times.

  Implementation ==> add
-- for debugging only
    import OutputForm
    import OutputPackage
-- end debugging
    import FactoredFunctions(P)
    import PolynomialCategoryLifting(IndexedExponents K, K, R, P, F)
    import
      PolynomialCategoryQuotientFunctions(IndexedExponents K,K,R,P,F)

    smpexp    : P -> F
    termexp   : P -> F
    exlog     : P -> F
    smplog    : P -> F
    smpexpand : P -> F
    smp2htrigs: P -> F
    kerexpand : K -> F
    expandpow : K -> F
    logexpand : K -> F
    sup2htrigs: (UP, F) -> F
    supexp    : (UP, F, F, Z) -> F
    ueval     : (F, String, F -> F) -> F
    ueval2    : (F, String, F -> F) -> F
    powersimp : (P, List K) -> F
    t2t       : F -> F
    c2t       : F -> F
    c2s       : F -> F
    s2c       : F -> F
    s2c2      : F -> F
    th2th     : F -> F
    ch2th     : F -> F
    ch2sh     : F -> F
    sh2ch     : F -> F
    sh2ch2    : F -> F
    simplify0 : F -> F
    simplifyLog1 : F -> F
    logArgs   : List F -> F

    import F
    import List F

    if R has PatternMatchable R and R has ConvertibleTo Pattern R and F has ConvertibleTo(Pattern(R)) and F has PatternMatchable R then
      XX : F := coerce new()$Symbol
      YY : F := coerce new()$Symbol
      sinCosRule : RewriteRule(R,R,F) :=
        rule(cos(XX)*sin(YY),(sin(XX+YY)-sin(XX-YY))/2::F)
      sinSinRule : RewriteRule(R,R,F) :=
        rule(sin(XX)*sin(YY),(cos(XX-YY)-cos(XX+YY))/2::F)
      cosCosRule : RewriteRule(R,R,F) :=
        rule(cos(XX)*cos(YY),(cos(XX-YY)+cos(XX+YY))/2::F)
      expandTrigProducts(e:F):F ==
        applyRules([sinCosRule,sinSinRule,cosCosRule],e,10)$ApplyRules(R,R,F)

    logArgs(l:List F):F ==
      -- This function will take a list of Expressions (implicitly a sum) and
      -- add them up, combining log terms.  It also replaces n*log(x) by
      -- log(x^n).
      import K
      sum  : F := 0
      arg  : F := 1
      for term in l repeat
        is?(term,"log"::Symbol) =>
          arg := arg * simplifyLog(first(argument(first(kernels(term)))))
        -- Now look for multiples, including negative ones.
        prod : Union(PRODUCT, "failed") := isMult(term)
        (prod case PRODUCT) and is?(prod.var,"log"::Symbol) =>
            arg := arg * simplifyLog ((first argument(prod.var))^(prod.coef))
        sum := sum+term
      sum+log(arg)

    simplifyLog(e:F):F ==
      simplifyLog1(numerator e)/simplifyLog1(denominator e)

    simplifyLog1(e:F):F ==
      freeOf?(e,"log"::Symbol) => e

      -- Check for n*log(u)
      prod : Union(PRODUCT, "failed") := isMult(e)
      (prod case PRODUCT) and is?(prod.var,"log"::Symbol) =>
        log simplifyLog ((first argument(prod.var))^(prod.coef))

      termList : Union(List(F),"failed") := isTimes(e)
      -- I'm using two variables, termList and terms, to work round a
      -- bug in the old compiler.
      not (termList case "failed") =>
        -- We want to simplify each log term in the product and then multiply
        -- them together.  However, if there is a constant or arithmetic
        -- expression (i.e. something which looks like a Polynomial) we would
        -- like to combine it with a log term.
        terms :List F := [simplifyLog(term) for term in termList::List(F)]
        exprs :List F := []
        for i in 1..#terms repeat
          if retractIfCan(terms.i)@Union(FPR,"failed") case FPR then
            exprs := cons(terms.i,exprs)
            terms := delete!(terms,i)
        if not empty? exprs then
          foundLog := false
          i : NonNegativeInteger := 0
          while (not(foundLog) and (i < #terms)) repeat
            i := i+1
            if is?(terms.i, 'log) then
              args : List F := argument(retract(terms.i)@K)
              setelt!(terms,i, log simplifyLog1(first(args)^(*/exprs)))
              foundLog := true
          -- The next line deals with a situation which shouldn't occur,
          -- since we have checked whether we are freeOf log already.
          if not foundLog then terms := append(exprs,terms)
        */terms

      terms : Union(List(F),"failed") := isPlus(e)
      not (terms case "failed") => logArgs(terms) 

      expt : Union(POW, "failed") := isPower(e)
--      (expt case POW) and not one? expt.exponent =>
      (expt case POW) and not (expt.exponent = 1) =>
        simplifyLog(expt.val)^(expt.exponent)

      kers : List K := kernels e
--      not(one?(#kers)) => e -- Have a constant
      not(((#kers) = 1)) => e -- Have a constant
      kernel(operator first kers,[simplifyLog(u) for u in argument first kers])

    if R has RetractableTo Integer then
      simplify x == rootProduct(simplify0 x)$AlgebraicManipulations(R,F)

    else simplify x == simplify0 x

    expandpow k ==
      a := expandPower first(arg := argument k)
      b := expandPower second arg
--      ne:F := (one? numer a => 1; numer(a)::F ^ b)
      ne:F := (((numer a) = 1) => 1; numer(a)::F ^ b)
--      de:F := (one? denom a => 1; denom(a)::F ^ (-b))
      de:F := (((denom a) = 1) => 1; denom(a)::F ^ (-b))
      ne * de

    termexp p ==
      exponent:F := 0
      coef := (leadingCoefficient p)::P
      lpow := select(xx +-> is?(xx, POWER)$K, lk := variables p)$List(K)
      for k in lk repeat
        d := degree(p, k)
        if is?(k, "exp"::Symbol) then
          exponent := exponent + d * first argument k
        else if not is?(k, POWER) then
          -- Expand arguments to functions as well ... MCD 23/1/97
          --coef := coef * monomial(1, k, d)
          coef := coef * monomial(1, kernel(operator k,[simplifyExp u for u in argument k], height k), d)
      coef::F * exp exponent * powersimp(p, lpow)

    expandPower f ==
      l := select(xx +-> is?(xx, POWER)$K, kernels f)$List(K)
      eval(f, l, [expandpow k for k in l])

-- l is a list of pure powers appearing as kernels in p
    powersimp(p, l) ==
      empty? l => 1
      k := first l                           -- k = a^b
      a := first(arg := argument k)
      exponent := degree(p, k) * second arg
      empty?(lk := select((xx : K) : Boolean +-> a = first argument xx, rest l)) =>
        (a ^ exponent) * powersimp(p, rest l)
      for k0 in lk repeat
        exponent := exponent + degree(p, k0) * second argument k0
      (a ^ exponent) * powersimp(p, setDifference(rest l, lk))

    t2t x         == sin(x) / cos(x)
    c2t x         == cos(x) / sin(x)
    c2s x         == inv sin x
    s2c x         == inv cos x
    s2c2 x        == 1 - cos(x)^2
    th2th x       == sinh(x) / cosh(x)
    ch2th x       == cosh(x) / sinh(x)
    ch2sh x       == inv sinh x
    sh2ch x       == inv cosh x
    sh2ch2 x      == cosh(x)^2 - 1
    ueval(x, s,f) == eval(x, s::Symbol, f)
    ueval2(x,s,f) == eval(x, s::Symbol, 2, f)
    cos2sec x     == ueval(x, "cos", xx +-> inv sec xx)
    sin2csc x     == ueval(x, "sin", xx +-> inv csc xx)
    csc2sin x     == ueval(x, "csc", c2s)
    sec2cos x     == ueval(x, "sec", s2c)
    tan2cot x     == ueval(x, "tan", xx +-> inv cot xx)
    cot2tan x     == ueval(x, "cot", xx +-> inv tan xx)
    tan2trig x    == ueval(x, "tan", t2t)
    cot2trig x    == ueval(x, "cot", c2t)
    cosh2sech x   == ueval(x, "cosh", xx +-> inv sech xx)
    sinh2csch x   == ueval(x, "sinh", xx +-> inv csch xx)
    csch2sinh x   == ueval(x, "csch", ch2sh)
    sech2cosh x   == ueval(x, "sech", sh2ch)
    tanh2coth x   == ueval(x, "tanh", xx +-> inv coth xx)
    coth2tanh x   == ueval(x, "coth", xx +-> inv tanh xx)
    tanh2trigh x  == ueval(x, "tanh", th2th)
    coth2trigh x  == ueval(x, "coth", ch2th)
    removeCosSq x == ueval2(x, "cos", xx +-> 1 - (sin xx)^2)
    removeSinSq x == ueval2(x, "sin", s2c2)
    removeCoshSq x== ueval2(x, "cosh", xx +-> 1 + (sinh xx)^2)
    removeSinhSq x== ueval2(x, "sinh", sh2ch2)
    expandLog x   == smplog(numer x) / smplog(denom x)
    simplifyExp x == (smpexp numer x) / (smpexp denom x)
    expand x      == (smpexpand numer x) / (smpexpand denom x)
    smpexpand p   == map(kerexpand, xx +-> xx::F, p)
    smplog p      == map(logexpand, xx +-> xx::F, p)
    smp2htrigs p  == map(htrigs(#1::F), xx+-> xx::F, p)

    htrigs f ==
      (m := mainKernel f) case "failed" => f
      op  := operator(k := m::K)
      arg := [htrigs x for x in argument k]$List(F)
      num := univariate(numer f, k)
      den := univariate(denom f, k)
      is?(op, "exp"::Symbol) =>
        g1 := cosh(a := first arg) + sinh(a)
        g2 := cosh(a) - sinh(a)
        supexp(num,g1,g2,b:= (degree num)::Z quo 2)/supexp(den,g1,g2,b)
      sup2htrigs(num, g1:= op arg) / sup2htrigs(den, g1)

    supexp(p, f1, f2, bse) ==
      ans:F := 0
      while p ~= 0 repeat
        g := htrigs(leadingCoefficient(p)::F)
        if ((d := degree(p)::Z - bse) >= 0) then
             ans := ans + g * f1 ^ d
        else ans := ans + g * f2 ^ (-d)
        p := reductum p
      ans

    sup2htrigs(p, f) ==
      (map(smp2htrigs, p)$SparseUnivariatePolynomialFunctions2(P, F)) f

    exlog p == +/[r.coef * log(r.logand::F) for r in log squareFree p]

    logexpand k ==
      nullary?(op := operator k) => k::F
      is?(op, "log"::Symbol) =>
         exlog(numer(x := expandLog first argument k)) - exlog denom x
      op [expandLog x for x in argument k]$List(F)

    kerexpand k ==
      nullary?(op := operator k) => k::F
      is?(op, POWER) => expandpow k
      arg := first argument k
      is?(op, "sec"::Symbol) => inv expand cos arg
      is?(op, "csc"::Symbol) => inv expand sin arg
      is?(op, "log"::Symbol) =>
         exlog(numer(x := expand arg)) - exlog denom x
      num := numer arg
      den := denom arg
      num := numer arg
      den := denom arg

-- for debugging output
      num := numer arg
      den := denom arg
      output(message "num:")
      output(num::OutputForm)
      output(message "den:")
      output(den::OutputForm)
-- end debugging

      (b := (reductum num) / den) ~= 0 =>
        a := (leadingMonomial num) / den
        is?(op, "exp"::Symbol) => exp(expand a) * expand(exp b)
        is?(op, "sin"::Symbol) =>
           sin(expand a) * expand(cos b) + cos(expand a) * expand(sin b)
        is?(op, "cos"::Symbol) =>
           cos(expand a) * expand(cos b) - sin(expand a) * expand(sin b)
        is?(op, "tan"::Symbol) =>
          ta := tan expand a
          tb := expand tan b
          (ta + tb) / (1 - ta * tb)
        is?(op, "cot"::Symbol) =>
          cta := cot expand a
          ctb := expand cot b
          (cta * ctb - 1) / (ctb + cta)
        op [expand x for x in argument k]$List(F)
      op [expand x for x in argument k]$List(F)

    smpexp p ==
      ans:F := 0
      while p ~= 0 repeat
        ans := ans + termexp leadingMonomial p
        p   := reductum p
      ans

    -- this now works in 3 passes over the expression:
    --   pass1 rewrites trigs and htrigs in terms of sin,cos,sinh,cosh
    --   pass2 rewrites sin^2 and sinh^2 in terms of cos and cosh.
    --   pass3 groups exponentials together
    simplify0 x ==
      simplifyExp eval(eval(x,
          ["tan"::Symbol,"cot"::Symbol,"sec"::Symbol,"csc"::Symbol,
           "tanh"::Symbol,"coth"::Symbol,"sech"::Symbol,"csch"::Symbol],
              [t2t,c2t,s2c,c2s,th2th,ch2th,sh2ch,ch2sh]),
                ["sin"::Symbol, "sinh"::Symbol], [2, 2], [s2c2, sh2ch2])</spad>

Compiling FriCAS source code from file 
      /var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/3219884400022380072-25px001.spad
      using old system compiler.
   TRMANIP2 abbreviates package TranscendentalManipulations2 
------------------------------------------------------------------------
   initializing NRLIB TRMANIP2 for TranscendentalManipulations2 
   compiling into NRLIB TRMANIP2 
****** Domain: R already in scope
****** Domain: F already in scope
   importing OutputForm
   importing OutputPackage
   importing FactoredFunctions SparseMultivariatePolynomial(R,Kernel F)
   importing PolynomialCategoryLifting(IndexedExponents Kernel F,Kernel F,R,SparseMultivariatePolynomial(R,Kernel F),F)
   importing PolynomialCategoryQuotientFunctions(IndexedExponents Kernel F,Kernel F,R,SparseMultivariatePolynomial(R,Kernel F),F)
   importing F
   importing List F
****** Domain: R already in scope
augmenting R: (PatternMatchable R)
****** Domain: R already in scope
augmenting R: (ConvertibleTo (Pattern R))
****** Domain: F already in scope
augmenting F: (ConvertibleTo (Pattern R))
****** Domain: F already in scope
augmenting F: (PatternMatchable R)
   compiling exported expandTrigProducts : F -> F
Time: 0.06 SEC.

   compiling local logArgs : List F -> F
Time: 0 SEC.

   compiling exported simplifyLog : F -> F
Time: 0 SEC.

   compiling local simplifyLog1 : F -> F
Local variable terms type redefined: (List F) to (Union (List F) failed)
Time: 0.01 SEC.

****** Domain: R already in scope
augmenting R: (RetractableTo (Integer))
   compiling exported simplify : F -> F
Time: 0 SEC.

   compiling exported simplify : F -> F
Time: 0 SEC.

   compiling local expandpow : Kernel F -> F
Time: 0.01 SEC.

   compiling local termexp : SparseMultivariatePolynomial(R,Kernel F) -> F
Time: 0.02 SEC.

   compiling exported expandPower : F -> F
Time: 0 SEC.

   compiling local powersimp : (SparseMultivariatePolynomial(R,Kernel F),List Kernel F) -> F
Time: 0.02 SEC.

   compiling local t2t : F -> F
Time: 0 SEC.

   compiling local c2t : F -> F
Time: 0 SEC.

   compiling local c2s : F -> F
Time: 0 SEC.

   compiling local s2c : F -> F
Time: 0 SEC.

   compiling local s2c2 : F -> F
Time: 0 SEC.

   compiling local th2th : F -> F
Time: 0 SEC.

   compiling local ch2th : F -> F
Time: 0 SEC.

   compiling local ch2sh : F -> F
Time: 0 SEC.

   compiling local sh2ch : F -> F
Time: 0 SEC.

   compiling local sh2ch2 : F -> F
Time: 0 SEC.

   compiling local ueval : (F,String,F -> F) -> F
Time: 0 SEC.

   compiling local ueval2 : (F,String,F -> F) -> F
Time: 0 SEC.

   compiling exported cos2sec : F -> F
Time: 0 SEC.

   compiling exported sin2csc : F -> F
Time: 0 SEC.

   compiling exported csc2sin : F -> F
Time: 0 SEC.

   compiling exported sec2cos : F -> F
Time: 0 SEC.

   compiling exported tan2cot : F -> F
Time: 0 SEC.

   compiling exported cot2tan : F -> F
Time: 0 SEC.

   compiling exported tan2trig : F -> F
Time: 0 SEC.

   compiling exported cot2trig : F -> F
Time: 0 SEC.

   compiling exported cosh2sech : F -> F
Time: 0 SEC.

   compiling exported sinh2csch : F -> F
Time: 0 SEC.

   compiling exported csch2sinh : F -> F
Time: 0 SEC.

   compiling exported sech2cosh : F -> F
Time: 0 SEC.

   compiling exported tanh2coth : F -> F
Time: 0 SEC.

   compiling exported coth2tanh : F -> F
Time: 0 SEC.

   compiling exported tanh2trigh : F -> F
Time: 0 SEC.

   compiling exported coth2trigh : F -> F
Time: 0 SEC.

   compiling exported removeCosSq : F -> F
Time: 0 SEC.

   compiling exported removeSinSq : F -> F
Time: 0 SEC.

   compiling exported removeCoshSq : F -> F
Time: 0 SEC.

   compiling exported removeSinhSq : F -> F
Time: 0 SEC.

   compiling exported expandLog : F -> F
Time: 0 SEC.

   compiling exported simplifyExp : F -> F
Time: 0 SEC.

   compiling exported expand : F -> F
Time: 0 SEC.

   compiling local smpexpand : SparseMultivariatePolynomial(R,Kernel F) -> F
Time: 0 SEC.

   compiling local smplog : SparseMultivariatePolynomial(R,Kernel F) -> F
Time: 0 SEC.

   compiling local smp2htrigs : SparseMultivariatePolynomial(R,Kernel F) -> F
Time: 0 SEC.

   compiling exported htrigs : F -> F
Time: 0 SEC.

   compiling local supexp : (SparseUnivariatePolynomial SparseMultivariatePolynomial(R,Kernel F),F,F,Integer) -> F
Time: 0.01 SEC.

   compiling local sup2htrigs : (SparseUnivariatePolynomial SparseMultivariatePolynomial(R,Kernel F),F) -> F
Time: 0 SEC.

   compiling local exlog : SparseMultivariatePolynomial(R,Kernel F) -> F
Time: 0 SEC.

   compiling local logexpand : Kernel F -> F
Time: 0 SEC.

   compiling local kerexpand : Kernel F -> F
Time: 0.01 SEC.

   compiling local smpexp : SparseMultivariatePolynomial(R,Kernel F) -> F
Time: 0 SEC.

   compiling local simplify0 : F -> F
Time: 0.05 SEC.

****** Domain: F already in scope
augmenting F: (ConvertibleTo (Pattern R))
****** Domain: F already in scope
augmenting F: (PatternMatchable R)
****** Domain: R already in scope
augmenting R: (ConvertibleTo (Pattern R))
****** Domain: R already in scope
augmenting R: (PatternMatchable R)
(time taken in buildFunctor:  310)

;;;     ***       |TranscendentalManipulations2| REDEFINED

;;;     ***       |TranscendentalManipulations2| REDEFINED
Time: 0 SEC.

   Warnings: 
      [1] logArgs:  var has no value
      [2] logArgs:  coef has no value
      [3] logArgs:  arg has no value
      [4] simplifyLog1:  var has no value
      [5] simplifyLog1:  coef has no value
      [6] simplifyLog1:  exponent has no value
      [7] simplifyLog1:  val has no value
      [8] simplifyLog1:  exprs has no value
      [9] simplifyLog1:  terms has no value
      [10] termexp:  exponent has no value
      [11] exlog:  coef has no value
      [12] exlog:  logand has no value
      [13] logexpand:  IN has no value
      [14] logexpand:  x has no value
      [15] kerexpand:  IN has no value
      [16] kerexpand:  x has no value

   Cumulative Statistics for Constructor TranscendentalManipulations2
      Time: 0.26 seconds

   finalizing NRLIB TRMANIP2 
   Processing TranscendentalManipulations2 for Browser database:
--------constructor---------
--------(expand (F F))---------
--------(simplify (F F))---------
--------(htrigs (F F))---------
--------(simplifyExp (F F))---------
--------(simplifyLog (F F))---------
--------(expandPower (F F))---------
--------(expandLog (F F))---------
--------(cos2sec (F F))---------
--------(cosh2sech (F F))---------
--------(cot2trig (F F))---------
--------(coth2trigh (F F))---------
--------(csc2sin (F F))---------
--------(csch2sinh (F F))---------
--------(sec2cos (F F))---------
--------(sech2cosh (F F))---------
--------(sin2csc (F F))---------
--------(sinh2csch (F F))---------
--------(tan2trig (F F))---------
--------(tanh2trigh (F F))---------
--------(tan2cot (F F))---------
--------(tanh2coth (F F))---------
--------(cot2tan (F F))---------
--------(coth2tanh (F F))---------
--------(removeCosSq (F F))---------
--------(removeSinSq (F F))---------
--------(removeCoshSq (F F))---------
--------(removeSinhSq (F F))---------
--------(expandTrigProducts (F F))---------
--->-->TranscendentalManipulations2((expandTrigProducts (F F))): Unexpected HT command: \axiom
--->-->TranscendentalManipulations2((expandTrigProducts (F F))): Unexpected HT command: \axiom
--->-->TranscendentalManipulations2((expandTrigProducts (F F))): Unexpected HT command: \axiom
"\\spad{expandTrigProducts(e)} replaces \\axiom{sin(\\spad{x})*sin(\\spad{y})} by \\spad{(cos(x-y)-cos(x+y))/2},{} \\axiom{cos(\\spad{x})*cos(\\spad{y})} by \\spad{(cos(x-y)+cos(x+y))/2},{} and \\axiom{sin(\\spad{x})*cos(\\spad{y})} by \\spad{(sin(x-y)+sin(x+y))/2}. Note that this operation uses the pattern matcher and so is relatively expensive. To avoid getting into an infinite loop the transformations are applied at most ten times."
; compiling file "/var/aw/var/LatexWiki/TRMANIP2.NRLIB/TRMANIP2.lsp" (written 06 OCT 2024 09:20:18 PM):

; wrote /var/aw/var/LatexWiki/TRMANIP2.NRLIB/TRMANIP2.fasl
; compilation finished in 0:00:00.200
------------------------------------------------------------------------
   TranscendentalManipulations2 is now explicitly exposed in frame 
      initial 
   TranscendentalManipulations2 will be automatically loaded when 
      needed from /var/aw/var/LatexWiki/TRMANIP2.NRLIB/TRMANIP2

Testing the change

-- old
ex1:=expandTrigProducts(sin(x)*sin(y))$TRMANIP(INT,Expression Integer)

(1)

ex2:=expand(ex1)$TRMANIP(INT,Expression Integer)

(2)

--new
ex3:=expand(ex1)$TRMANIP2(INT,Expression Integer)

   num:
   y + x
   den:
   1
   num:
   x
   den:
   1
   num:
   x
   den:
   1
   num:
   y - x
   den:
   1
   num:
   x
   den:
   1
   num:
   x
   den:
   1

(3)

sinCosProducts := rule
  sin(x)*sin(y) == (cos(x-y) - cos(x+y))/2
  cos(x)*cos(y) == (cos(x-y) + cos(x+y))/2
  sin(x)*cos(y) == (sin(x-y) + sin(x+y))/2
  sin(x)^2 == (1 - cos(2*x))/2
  sin(x)^3 == sin(x)*(1 - cos(2*x))/2

(4)