|
|
|
last edited 10 years ago by Bill Page |
Edit detail for SandBoxLorentzTransformation revision 1 of 30
| 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 | ||
|
Editor: Bill Page
Time: 2013/09/22 02:14:21 GMT+0 |
||
| Note: | ||
changed: - Lorentz transformations. Book by T. Matolcsi - "Space-time without reference frames":http://axiom-wiki.newsynthesis.org/uploads/matolcsi.pdf Mathematical Preliminaries A vector is represented as a nx1 matrix (column vector) \begin{axiom} vect(x:List Expression Integer):Matrix Expression Integer == matrix map(y+->[y],x) vect [a1,a2,a3] \end{axiom} Then a row vector is \begin{axiom} transpose(vect [a1,a2,a3]) \end{axiom} Tensor product is \begin{axiom} tensor(v,w) == v*transpose(w) tensor(vect [a1,a2,a3], vect [b1,b2,b3]) \end{axiom} Applying the Lorentz form produces a row vector \begin{axiom} g(x)==transpose(x)*diagonalMatrix [-1,1,1,1] \end{axiom} or a scalar \begin{axiom} g(x,y)== (transpose(x)*diagonalMatrix([-1,1,1,1])*y)::EXPR INT \end{axiom} For difficult verifications it is sometimes convenient to replace symbols by random numerical values. \begin{axiom} possible(x)==subst(x, map(y+->(y=(random(100) - random(100))),variables x) ) Is?(eq:Equation EXPR INT):Boolean == (lhs(eq)-rhs(eq)=0)::Boolean Is2?(eq:Equation(Matrix(EXPR(INT)))):Boolean == _ ( (lhs(eq)-rhs(eq)) :: Matrix Expression AlgebraicNumber = _ zero(nrows(lhs(eq)),ncols(lhs(eq)))$Matrix Expression AlgebraicNumber )::Boolean \end{axiom} The AlgebraicNumber domain can test for numerical equality of complicated expressions involving $\sqrt{n}$. \begin{axiom} IsPossible?(eq:Equation EXPR INT):Boolean == _ (possible(lhs(eq)-rhs(eq)) :: Expression AlgebraicNumber=0)::Boolean IsPossible2?(eq:Equation(Matrix(EXPR(INT)))):Boolean == _ ( map(possible,(lhs(eq)-rhs(eq))) :: Matrix Expression AlgebraicNumber = _ zero(nrows(lhs(eq)),ncols(lhs(eq)))$Matrix Expression AlgebraicNumber )::Boolean \end{axiom} Massive Objects An object (also referred to as an obserser) is represented by a time-like 4-vector \begin{axiom} P:=vect [sqrt(p1^2+p2^2+p3^2+1),p1,p2,p3]; g(P,P) Q:=vect [sqrt(q1^2+q2^2+q3^2+1),q1,q2,q3]; g(Q,Q) R:=vect [1,0,0,0] g(R,R) \end{axiom} Associated with each such vector is the orthogonal 3-d Euclidean subspace $E_P =\{x | P \cdot x = 0\}$ Relative Velocity An object Q has a unique relative velocity w(P,Q) with respect to object P given by \begin{axiom} w(P,Q)==-Q/g(P,Q)-P \end{axiom} Lorentz factor \begin{axiom} gamma(v)==1/sqrt(1-g(v,v)) \end{axiom} Binary Boost \begin{axiom} b(P,v)==gamma(v)*(P+v) \end{axiom} Observer P measures velocity u. u is space-like and in $E_P$. \begin{axiom} u:=w(P,Q); g(P,u) possible(g(u,u))::EXPR Float \end{axiom} \begin{axiom} L(P,Q) == diagonalMatrix([1,1,1,1]) + tensor(P+Q,P+Q)/g(P,Q) - 2*tensor(P,Q) L(P,R) L(P,R)*P \end{axiom}
Lorentz transformations.
Book by T. Matolcsi
Mathematical Preliminaries
A vector is represented as a nx1 matrix (column vector)
fricas
vect(x:List Expression Integer):Matrix Expression Integer == matrix map(y+->[y],x)
Function declaration vect : List(Expression(Integer)) -> Matrix( Expression(Integer)) has been added to workspace.
Type: Void
fricas
vect [a1,a2, a3]
fricas
Compiling function vect with type List(Expression(Integer)) ->
Matrix(Expression(Integer))![\label{eq1}\left[
\begin{array}{c}
a 1
\
a 2
\
a 3](images/4675740844508318613-16.0px.png "\label{eq1}\left[
\begin{array}{c}
a 1
\
a 2
\
a 3") | (1) |
Type: Matrix(Expression(Integer))
Then a row vector is
fricas
transpose(vect [a1,a2, a3])
 | (2) |
Type: Matrix(Expression(Integer))
Tensor product is
fricas
tensor(v,w) == v*transpose(w)
Type: Void
fricas
tensor(vect [a1,a2, a3], vect [b1, b2, b3])
fricas
Compiling function tensor with type (Matrix(Expression(Integer)),Matrix(Expression(Integer))) -> Matrix(Expression(Integer))
![\label{eq3}\left[
\begin{array}{ccc}
{a 1 \ b 1}&{a 1 \ b 2}&{a 1 \ b 3}
\
{a 2 \ b 1}&{a 2 \ b 2}&{a 2 \ b 3}
\
{a 3 \ b 1}&{a 3 \ b 2}&{a 3 \ b 3}](images/7701774881545240493-16.0px.png "\label{eq3}\left[
\begin{array}{ccc}
{a 1 \ b 1}&{a 1 \ b 2}&{a 1 \ b 3}
\
{a 2 \ b 1}&{a 2 \ b 2}&{a 2 \ b 3}
\
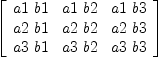{a 3 \ b 1}&{a 3 \ b 2}&{a 3 \ b 3}") | (3) |
Type: Matrix(Expression(Integer))
Applying the Lorentz form produces a row vector
fricas
g(x)==transpose(x)*diagonalMatrix [-1,1, 1, 1]
Type: Void
or a scalar
fricas
g(x,y)== (transpose(x)*diagonalMatrix([-1, 1, 1, 1])*y)::EXPR INT
Type: Void
For difficult verifications it is sometimes convenient to replace symbols by random numerical values.
fricas
possible(x)==subst(x,map(y+->(y=(random(100) - random(100))), variables x) )
Type: Void
fricas
Is?(eq:Equation EXPR INT):Boolean == (lhs(eq)-rhs(eq)=0)::Boolean
Function declaration Is? : Equation(Expression(Integer)) -> Boolean has been added to workspace.
Type: Void
fricas
Is2?(eq:Equation(Matrix(EXPR(INT)))):Boolean == _ ( (lhs(eq)-rhs(eq)) :: Matrix Expression AlgebraicNumber = _ zero(nrows(lhs(eq)),ncols(lhs(eq)))$Matrix Expression AlgebraicNumber )::Boolean
Function declaration Is2? : Equation(Matrix(Expression(Integer))) -> Boolean has been added to workspace.
Type: Void
The AlgebraicNumber? domain can test for numerical equality of complicated
expressions involving 
.
fricas
IsPossible?(eq:Equation EXPR INT):Boolean == _ (possible(lhs(eq)-rhs(eq)) :: Expression AlgebraicNumber=0)::Boolean
Function declaration IsPossible? : Equation(Expression(Integer)) -> Boolean has been added to workspace.
Type: Void
fricas
IsPossible2?(eq:Equation(Matrix(EXPR(INT)))):Boolean == _ ( map(possible,(lhs(eq)-rhs(eq))) :: Matrix Expression AlgebraicNumber = _ zero(nrows(lhs(eq)), ncols(lhs(eq)))$Matrix Expression AlgebraicNumber )::Boolean
Function declaration IsPossible2? : Equation(Matrix(Expression( Integer))) -> Boolean has been added to workspace.
Type: Void
Massive Objects
An object (also referred to as an obserser) is represented by a time-like 4-vector
fricas
P:=vect [sqrt(p1^2+p2^2+p3^2+1),p1, p2, p3];
Type: Matrix(Expression(Integer))
fricas
g(P,P)
fricas
Compiling function g with type (Matrix(Expression(Integer)),Matrix( Expression(Integer))) -> Expression(Integer)
 | (4) |
Type: Expression(Integer)
fricas
Q:=vect [sqrt(q1^2+q2^2+q3^2+1),q1, q2, q3];
Type: Matrix(Expression(Integer))
fricas
g(Q,Q)
 | (5) |
Type: Expression(Integer)
fricas
R:=vect [1,0, 0, 0]
![\label{eq6}\left[
\begin{array}{c}
1
\
0
\
0
\
0](images/6345508732508486706-16.0px.png "\label{eq6}\left[
\begin{array}{c}
1
\
0
\
0
\
0") | (6) |
Type: Matrix(Expression(Integer))
fricas
g(R,R)
 | (7) |
Type: Expression(Integer)
Associated with each such vector is the orthogonal 3-d Euclidean subspace
Relative Velocity
An object Q has a unique relative velocity w(P,Q) with respect to object P given by
fricas
w(P,Q)==-Q/g(P, Q)-P
Type: Void
Lorentz factor
fricas
gamma(v)==1/sqrt(1-g(v,v))
Type: Void
Binary Boost
fricas
b(P,v)==gamma(v)*(P+v)
Type: Void
Observer P measures velocity u. u is space-like and in 
.
fricas
u:=w(P,Q);
fricas
Compiling function w with type (Matrix(Expression(Integer)),Matrix( Expression(Integer))) -> Matrix(Expression(Integer))
Type: Matrix(Expression(Integer))
fricas
g(P,u)
 | (8) |
Type: Expression(Integer)
fricas
possible(g(u,u))::EXPR Float
fricas
Compiling function possible with type Expression(Integer) ->
Expression(Integer) | (9) |
Type: Expression(Float)
fricas
L(P,Q) == diagonalMatrix([1, 1, 1, 1]) + tensor(P+Q, P+Q)/g(P, Q) - 2*tensor(P, Q)
Type: Void
fricas
L(P,R)
fricas
Compiling function L with type (Matrix(Expression(Integer)),Matrix( Expression(Integer))) -> Matrix(Expression(Integer))
![\label{eq10}\left[
\begin{array}{cccc}
{{-{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}-{3 \ {{p 3}^{2}}}-{3 \ {{p 2}^{2}}}-{3 \ {{p 1}^{2}}}- 4}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}&{{-{p 1 \ {\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}- p 1}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}&{{-{p 2 \ {\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}- p 2}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}&{{-{p 3 \ {\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}- p 3}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}
\
{{-{3 \ p 1 \ {\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}- p 1}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}&{{{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}-{{p 1}^{2}}}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}& -{{p 1 \ p 2}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}& -{{p 1 \ p 3}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}
\
{{-{3 \ p 2 \ {\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}- p 2}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}& -{{p 1 \ p 2}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}&{{{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}-{{p 2}^{2}}}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}& -{{p 2 \ p 3}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}
\
{{-{3 \ p 3 \ {\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}- p 3}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}& -{{p 1 \ p 3}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}& -{{p 2 \ p 3}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}&{{{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}-{{p 3}^{2}}}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}](images/1481050632253992612-16.0px.png "\label{eq10}\left[
\begin{array}{cccc}
{{-{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}-{3 \ {{p 3}^{2}}}-{3 \ {{p 2}^{2}}}-{3 \ {{p 1}^{2}}}- 4}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}&{{-{p 1 \ {\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}- p 1}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}&{{-{p 2 \ {\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}- p 2}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}&{{-{p 3 \ {\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}- p 3}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}
\
{{-{3 \ p 1 \ {\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}- p 1}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}&{{{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}-{{p 1}^{2}}}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}& -{{p 1 \ p 2}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}& -{{p 1 \ p 3}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}
\
{{-{3 \ p 2 \ {\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}- p 2}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}& -{{p 1 \ p 2}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}&{{{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}-{{p 2}^{2}}}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}& -{{p 2 \ p 3}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}
\
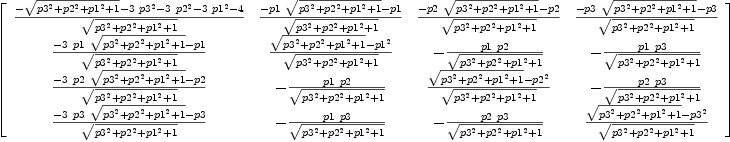{{-{3 \ p 3 \ {\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}- p 3}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}& -{{p 1 \ p 3}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}& -{{p 2 \ p 3}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}&{{{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}-{{p 3}^{2}}}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}") | (10) |
Type: Matrix(Expression(Integer))
fricas
L(P,R)*P
![\label{eq11}\left[
\begin{array}{c}
{{{{\left(-{4 \ {{p 3}^{2}}}-{4 \ {{p 2}^{2}}}-{4 \ {{p 1}^{2}}}- 4 \right)}\ {\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}-{2 \ {{p 3}^{2}}}-{2 \ {{p 2}^{2}}}-{2 \ {{p 1}^{2}}}- 1}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}
\
{{-{4 \ p 1 \ {{p 3}^{2}}}-{4 \ p 1 \ {{p 2}^{2}}}-{4 \ {{p 1}^{3}}}-{3 \ p 1}}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}
\
{{-{4 \ p 2 \ {{p 3}^{2}}}-{4 \ {{p 2}^{3}}}+{{\left(-{4 \ {{p 1}^{2}}}- 3 \right)}\ p 2}}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}
\
{{-{4 \ {{p 3}^{3}}}+{{\left(-{4 \ {{p 2}^{2}}}-{4 \ {{p 1}^{2}}}- 3 \right)}\ p 3}}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}](images/5789614280779159398-16.0px.png "\label{eq11}\left[
\begin{array}{c}
{{{{\left(-{4 \ {{p 3}^{2}}}-{4 \ {{p 2}^{2}}}-{4 \ {{p 1}^{2}}}- 4 \right)}\ {\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}-{2 \ {{p 3}^{2}}}-{2 \ {{p 2}^{2}}}-{2 \ {{p 1}^{2}}}- 1}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}
\
{{-{4 \ p 1 \ {{p 3}^{2}}}-{4 \ p 1 \ {{p 2}^{2}}}-{4 \ {{p 1}^{3}}}-{3 \ p 1}}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}
\
{{-{4 \ p 2 \ {{p 3}^{2}}}-{4 \ {{p 2}^{3}}}+{{\left(-{4 \ {{p 1}^{2}}}- 3 \right)}\ p 2}}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}
\
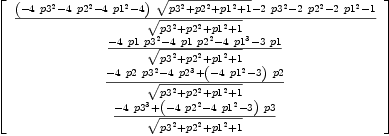{{-{4 \ {{p 3}^{3}}}+{{\left(-{4 \ {{p 2}^{2}}}-{4 \ {{p 1}^{2}}}- 3 \right)}\ p 3}}\over{\sqrt{{{p 3}^{2}}+{{p 2}^{2}}+{{p 1}^{2}}+ 1}}}") | (11) |
Type: Matrix(Expression(Integer))