help links subscribe changes refresh edit

	Frobenius Algebra, Vector Spaces and Polynomial Ideals
Octonion Algebra is Frobenius in Just One Way ←	↑	→ SandBox Quaternion Algebra is Frobenius in Many Ways

SandBox Grassmann Algebra Is Frobenius In Many Ways

Edit detail for SandBox Grassmann Algebra Is Frobenius In Many Ways revision 8 of 8

	1 2 3 4 5 6 7 8
Editor: Bill Page Time: 2011/06/08 20:40:40 GMT-7
Note: snails, turtles and deer

changed:
---eigenvectors(u1::Matrix FRAC POLY INT)
-\end{axiom}
\end{axiom}

\begin{axiom}
)set output algebra on
)set output tex off
\end{axiom}
\begin{axiom}
eigenvectors(u1::Matrix FRAC POLY INT)
\end{axiom}
\begin{axiom}
)set output algebra off
)set output tex on
\end{axiom}

changed:
-  (  Y  Y )
  (  Y Y  )

added:
Bi-algebra conditions
\begin{axiom}
ΦΦ:=          _
  (  λ λ  ) / _
  ( I X I ) / _
  (  Y Y  )
test((e,e)/ΦΦ=φφ)
\end{axiom}

Y-forms

  Three traces of two graftings of an algebra gives six
(2,0)-forms.

Left snail and right snail::

  LS                    RS

  Y /\                    /\ Y
   Y  )                  (  Y
    \/                    \/

  i  j                        j  i
   \/                          \/
    \    /\              /\    /
     e  f  \            /  f  e
      \/    \          /    \/
       \    /          \    /
        f  /            \  f
         \/              \/

\begin{axiom}
LS:=
  ( Y Λ  )/ _
  (  Y I )/ _
      V
RS:=
  (  Λ Y )/ _
  ( I Y  )/ _
     V
test(LS=RS)
\end{axiom}

Left and right deer::

   RD                 LD

   \ /\/              \/\ /
    Y /\              /\ Y
     Y  )            (  Y
      \/              \/

   i            j    i            j
    \    /\    /      \    /\    /
     \  f  \  /        \  /  f  /
      \/    \/          \/    \/
       \    /\          /\    /
        e  /  \        /  \  e
         \/    \      /    \/
          \    /      \    /
           f  /        \  f
            \/          \/

Left and right deer forms are identical but different from snails.
\begin{axiom}
RD:=
  (  I Λ I  ) / _
  (   Y X   ) / _
  (    Y I  ) / _
        V
LD:=
  (  I Λ I  ) / _
  (   X Y   ) / _
  (  I Y    ) / _
      V
test(LD=RD)
test(RD=RS)
test(RD=LS)
\end{axiom}

Left and right turtles::

  RT                   LT

   /\ / /               \ \ /\
  (  Y /                 \ Y  )
   \  Y                   Y  /
    \/                     \/

           i     j      i     j
    /\    /     /        \     \    /\
   /  f  /     /          \     \  f  \
  /    \/     /            \     \/    \
  \     \    /              \    /     /
   \     e  /                \  e     /
    \     \/                  \/     /
     \    /                    \    /
      \  f                      f  /
       \/                        \/

\begin{axiom}
RT:=
  (  Λ I I ) / _
  ( I Y I  ) / _
  (  I Y   ) / _
      V
LT:=
  ( I I Λ  ) / _
  (  I Y I ) / _
  (   Y I  ) / _
       V
test(LT=RT)
\end{axiom}
The turles are symmetric
\begin{axiom}
test(RT = X/RT)
test(LT = X/LT)
\end{axiom}
Five of the six forms are independent.
\begin{axiom}
test(RT=RS)
test(RT=LS)
test(RT=RD)
test(LT=RS)
test(LT=LS)
test(LT=RD)
\end{axiom}

Grassmann Algebra Is Frobenius In Many Ways

A -dimensional vector space represents Grassmann algebra with generators

Linear operators over a 4-dimensional vector space representing Grassmann algebra with two generators.

Ref:

http://arxiv.org/abs/1103.5113
-permuted Frobenius Algebras

Zbigniew Oziewicz (UNAM), Gregory Peter Wene (UTSA)
http://mat.uab.es/~kock/TQFT.html
Frobenius algebras and 2D topological quantum field theories

Joachim Kock
http://en.wikipedia.org/wiki/Frobenius_algebra
http://en.wikipedia.org/wiki/Grassmann_algebra

We need the Axiom LinearOperator library.

fricas

(1) -> )library CARTEN ARITY CMONAL CPROP CLOP CALEY

   >> System error:
   The value
  15684
is not of type
  LIST

Use the following macros for convenient notation

fricas

-- summation
macro Σ(x,i,n)==reduce(+,[x for i in n])

Type: Void

fricas

-- list
macro Ξ(f,i,n)==[f for i in n]

Type: Void

fricas

-- subscript and superscripts
macro sb == subscript

Type: Void

fricas

macro sp == superscript

Type: Void

𝐋 is the domain of 4-dimensional linear operators over the rational functions ℚ (Expression Integer), i.e. ratio of polynomials with integer coefficients.

fricas

dim:=4

$\label{eq1}4$

(1)

Type: PositiveInteger?

fricas

macro ℒ == List

Type: Void

fricas

macro ℂ == CaleyDickson

Type: Void

fricas

macro ℚ == Expression Integer

Type: Void

fricas

𝐋 := ClosedLinearOperator(OVAR ['1,'i,'j,'k], ℚ)

   There are no library operations named ClosedLinearOperator 
      Use HyperDoc Browse or issue
                        )what op ClosedLinearOperator
      to learn if there is any operation containing " 
      ClosedLinearOperator " in its name.

   Cannot find a definition or applicable library operation named 
      ClosedLinearOperator with argument type(s) 
                                    Type
                                    Type

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Generate structure constants for Grassmann Algebra

The structure constants can be obtained by dividing each matrix entry by the list of basis vectors.

Grassmann algebra will be specified by setting the Caley-Dickson parameters (i2, j2) to zero.

fricas

i2:=sp('i,[2])

$\label{eq2}i^{2}$

(2)

Type: Symbol

fricas

j2:=sp('j,[2])

$\label{eq3}j^{2}$

(3)

Type: Symbol

fricas

QQ:=CliffordAlgebra(2,ℚ,matrix [[i2,0],[0,j2]])

$\label{eq4}\hbox{\axiomType{CliffordAlgebra}\ } \left({2, \:{\hbox{\axiomType{Expression}\ } \left({\hbox{\axiomType{Integer}\ }}\right)}, \:{\left[ \begin{array}{cc} {i^{2}}& 0 \ 0 &{j^{2}}$

(4)

Type: Type

fricas

B:ℒ QQ := [monomial(1,[]),monomial(1,[1]),monomial(1,[2]),monomial(1,[1,2])]

$\label{eq5}\left[ 1, \:{e_{1}}, \:{e_{2}}, \:{{e_{1}}\ {e_{2}}}\right]$

(5)

Type: List(CliffordAlgebra?(2,Expression(Integer),[[i[;2],0],[0,j[;2]]]))

fricas

M:Matrix QQ := matrix Ξ(Ξ(B.i*B.j, i,1..dim), j,1..dim)

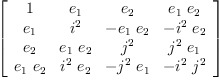$\label{eq6}\left[ \begin{array}{cccc} 1 &{e_{1}}&{e_{2}}&{{e_{1}}\ {e_{2}}} \ {e_{1}}&{i^{2}}& -{{e_{1}}\ {e_{2}}}& -{{i^{2}}\ {e_{2}}} \ {e_{2}}&{{e_{1}}\ {e_{2}}}&{j^{2}}&{{j^{2}}\ {e_{1}}} \ {{e_{1}}\ {e_{2}}}&{{i^{2}}\ {e_{2}}}& -{{j^{2}}\ {e_{1}}}& -{{i^{2}}\ {j^{2}}}$

(6)

Type: Matrix(CliffordAlgebra?(2,Expression(Integer),[[i[;2],0],[0,j[;2]]]))

fricas

S(y) == map(x +-> coefficient(recip(y)*x,[]),M)

Type: Void

fricas

ѕ :=map(S,B)::ℒ ℒ ℒ ℚ

fricas

Compiling function S with type CliffordAlgebra(2,Expression(Integer)
      ,[[i[;2],0],[0,j[;2]]]) -> Matrix(Expression(Integer))

$\label{eq7}\begin{array}{@{}l} \displaystyle \left[{\left[{\left[ 1, \: 0, \: 0, \: 0 \right]}, \:{\left[ 0, \:{i^{2}}, \: 0, \: 0 \right]}, \:{\left[ 0, \: 0, \:{j^{2}}, \: 0 \right]}, \:{\left[ 0, \: 0, \: 0, \: -{{i^{2}}\ {j^{2}}}\right]}\right]}, \: \right. \ \ \displaystyle \left.{\left[{\left[ 0, \: 1, \: 0, \: 0 \right]}, \:{\left[ 1, \: 0, \: 0, \: 0 \right]}, \:{\left[ 0, \: 0, \: 0, \:{j^{2}}\right]}, \:{\left[ 0, \: 0, \: -{j^{2}}, \: 0 \right]}\right]}, \: \right. \ \ \displaystyle \left.{\left[{\left[ 0, \: 0, \: 1, \: 0 \right]}, \:{\left[ 0, \: 0, \: 0, \: -{i^{2}}\right]}, \:{\left[ 1, \: 0, \: 0, \: 0 \right]}, \:{\left[ 0, \:{i^{2}}, \: 0, \: 0 \right]}\right]}, \: \right. \ \ \displaystyle \left.{\left[{\left[ 0, \: 0, \: 0, \: 1 \right]}, \:{\left[ 0, \: 0, \: - 1, \: 0 \right]}, \:{\left[ 0, \: 1, \: 0, \: 0 \right]}, \:{\left[ 1, \: 0, \: 0, \: 0 \right]}\right]}\right]$

(7)

Type: List(List(List(Expression(Integer))))

fricas

-- structure constants form a tensor operator
--Y := Σ(Σ(Σ(ѕ(i)(k)(j)*𝐞.i*𝐝.j*𝐝.k, i,1..dim), j,1..dim), k,1..dim)
Y := eval(Σ(Σ(Σ(ѕ(i)(k)(j)*𝐞.i*𝐝.j*𝐝.k, i,1..dim), j,1..dim), k,1..dim),[i2=0,j2=0])

   There are no library operations named 𝐞 
      Use HyperDoc Browse or issue
                                 )what op 𝐞
      to learn if there is any operation containing " 𝐞 " in its name.
   Cannot find a definition or applicable library operation named 𝐞 
      with argument type(s) 
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
   FriCAS will attempt to step through and interpret the code.
   There are no library operations named 𝐞 
      Use HyperDoc Browse or issue
                                 )what op 𝐞
      to learn if there is any operation containing " 𝐞 " in its name.

   Cannot find a definition or applicable library operation named 𝐞 
      with argument type(s) 
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Units

fricas

e:=𝐞.1; i:=𝐞.2; j:=𝐞.3; k:=𝐞.4;

   There are no library operations named 𝐞 
      Use HyperDoc Browse or issue
                                 )what op 𝐞
      to learn if there is any operation containing " 𝐞 " in its name.

   Cannot find a definition or applicable library operation named 𝐞 
      with argument type(s) 
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Multiplication of arbitrary Grassmann numbers and

fricas

a:=Σ(sb('a,[i])*𝐞.i, i,1..dim)

   There are no library operations named 𝐞 
      Use HyperDoc Browse or issue
                                 )what op 𝐞
      to learn if there is any operation containing " 𝐞 " in its name.
   Cannot find a definition or applicable library operation named 𝐞 
      with argument type(s) 
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
   FriCAS will attempt to step through and interpret the code.
   There are no library operations named 𝐞 
      Use HyperDoc Browse or issue
                                 )what op 𝐞
      to learn if there is any operation containing " 𝐞 " in its name.

   Cannot find a definition or applicable library operation named 𝐞 
      with argument type(s) 
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Multiplication is Associative

fricas

test(
  ( I Y ) / _
  (  Y  ) = _
  ( Y I ) / _
  (  Y  ) )

   There are no exposed library operations named I but there is one 
      unexposed operation with that name. Use HyperDoc Browse or issue
                                )display op I
      to learn more about the available operation.

   Cannot find a definition or applicable library operation named I 
      with argument type(s) 
                                 Variable(Y)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

A scalar product is denoted by the (2,0)-tensor $U = \{ u_{ij} \}$

fricas

U:=Σ(Σ(script('u,[[],[i,j]])*𝐝.i*𝐝.j, i,1..dim), j,1..dim)

   There are no library operations named 𝐝 
      Use HyperDoc Browse or issue
                                 )what op 𝐝
      to learn if there is any operation containing " 𝐝 " in its name.
   Cannot find a definition or applicable library operation named 𝐝 
      with argument type(s) 
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
   FriCAS will attempt to step through and interpret the code.
   There are no library operations named 𝐝 
      Use HyperDoc Browse or issue
                                 )what op 𝐝
      to learn if there is any operation containing " 𝐝 " in its name.

   Cannot find a definition or applicable library operation named 𝐝 
      with argument type(s) 
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Definition 1

We say that the scalar product is associative if the tensor equation holds:

    Y   =   Y
     U     U

In other words, if the (3,0)-tensor:

$\scalebox{1} % Change this value to rescale the drawing. { \begin{pspicture}(0,-0.92)(4.82,0.92) \psbezier[linewidth=0.04](2.2,0.9)(2.2,0.1)(2.6,0.1)(2.6,0.9) \psline[linewidth=0.04cm](2.4,0.3)(2.4,-0.1) \psbezier[linewidth=0.04](2.4,-0.1)(2.4,-0.9)(3.0,-0.9)(3.0,-0.1) \psline[linewidth=0.04cm](3.0,-0.1)(3.0,0.9) \psbezier[linewidth=0.04](4.8,0.9)(4.8,0.1)(4.4,0.1)(4.4,0.9) \psline[linewidth=0.04cm](4.6,0.3)(4.6,-0.1) \psbezier[linewidth=0.04](4.6,-0.1)(4.6,-0.9)(4.0,-0.9)(4.0,-0.1) \psline[linewidth=0.04cm](4.0,-0.1)(4.0,0.9) \usefont{T1}{ptm}{m}{n} \rput(3.4948437,0.205){-} \psline[linewidth=0.04cm](0.6,-0.7)(0.6,0.9) \psbezier[linewidth=0.04](0.0,-0.1)(0.0,-0.9)(1.2,-0.9)(1.2,-0.1) \psline[linewidth=0.04cm](0.0,-0.1)(0.0,0.9) \psline[linewidth=0.04cm](1.2,-0.1)(1.2,0.9) \usefont{T1}{ptm}{m}{n} \rput(1.6948438,0.205){=} \end{pspicture} }$

$\label{eq8} \Phi = \{ \phi^{ijk} = {y^e}_{ij} u_{ek} - u_{ie} {y_e}^{jk} \}$

(8)

(three-point function) is zero.

Using the LinearOperator domain in Axiom and some carefully chosen symbols we can easily enter expressions that are both readable and interpreted by Axiom as "graphical calculus" diagrams describing complex products and compositions of linear operators.

fricas

ω:𝐋 :=
     (    Y I    )  /
           U        -
     (    I Y    )  /
           U

   𝐋 is not a valid type.

Definition 2

An algebra with a non-degenerate associative scalar product is called a [Frobenius Algebra]?.

The Cartan-Killing Trace

fricas

Ú:=
   (  Y Λ  ) / _
   (   Y I ) / _
        V

   There are no exposed library operations named Y but there are 2 
      unexposed operations with that name. Use HyperDoc Browse or issue
                                )display op Y
      to learn more about the available operations.

   Cannot find a definition or applicable library operation named Y 
      with argument type(s) 
                                 Variable(Λ)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

forms is degenerate

fricas

Ũ := Ù

$\label{eq9}��$

(9)

Type: Variable(Ù)

fricas

test
     (    Y I    )  /
           Ũ        =
     (    I Y    )  /
           Ũ

   There are no exposed library operations named Y but there are 2 
      unexposed operations with that name. Use HyperDoc Browse or issue
                                )display op Y
      to learn more about the available operations.

   Cannot find a definition or applicable library operation named Y 
      with argument type(s) 
                                 Variable(I)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

General Solution

We may consider the problem where multiplication Y is given, and look for all associative scalar products

This problem can be solved using linear algebra.

fricas

)expose MCALCFN

   MultiVariableCalculusFunctions is now explicitly exposed in frame 
      initial 
J := jacobian(ravel ω,concat map(variables,ravel U)::ℒ Symbol);

   There are 1 exposed and 0 unexposed library operations named ravel 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op ravel
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named ravel
      with argument type(s) 
                                 Variable(ω)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

The matrix J transforms the coefficients of the tensor into coefficients of the tensor $\Phi$ . We are looking for the general linear family of tensors such that J transforms into $\Phi=0$ for any such .

If the null space of the J matrix is not empty we can use the basis to find all non-trivial solutions for U:

fricas

Ñ:=nullSpace(J)

   There are 3 exposed and 3 unexposed library operations named 
      nullSpace having 1 argument(s) but none was determined to be 
      applicable. Use HyperDoc Browse, or issue
                            )display op nullSpace
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named 
      nullSpace with argument type(s) 
                                 Variable(J)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

This defines a family of pre-Frobenius algebras:

fricas

zero? eval(ω,ℰ)

   There are 10 exposed and 6 unexposed library operations named eval 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                              )display op eval
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named eval 
      with argument type(s) 
                                 Variable(ω)
                                 Variable(ℰ)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Frobenius Form (co-unit)

fricas

d:=ε1*𝐝.1+εi*𝐝.2+εj*𝐝.3+εk*𝐝.4

   There are no library operations named 𝐝 
      Use HyperDoc Browse or issue
                                 )what op 𝐝
      to learn if there is any operation containing " 𝐝 " in its name.

   Cannot find a definition or applicable library operation named 𝐝 
      with argument type(s) 
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Express scalar product in terms of Frobenius form

fricas

𝔓:=solve(𝔇,Ξ(sb('p,[i]), i,1..#Ñ)).1

   There are 2 exposed and 2 unexposed library operations named # 
      having 1 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op #
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named # 
      with argument type(s) 
                                 Variable(Ñ)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

In general the pairing is not symmetric!

fricas

u1:=matrix Ξ(Ξ(retract((𝐞.i 𝐞.j)/Ų), i,1..dim), j,1..dim)

   There are no library operations named 𝐞 
      Use HyperDoc Browse or issue
                                 )what op 𝐞
      to learn if there is any operation containing " 𝐞 " in its name.
   Cannot find a definition or applicable library operation named 𝐞 
      with argument type(s) 
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
   FriCAS will attempt to step through and interpret the code.
   There are no library operations named 𝐞 
      Use HyperDoc Browse or issue
                                 )what op 𝐞
      to learn if there is any operation containing " 𝐞 " in its name.

   Cannot find a definition or applicable library operation named 𝐞 
      with argument type(s) 
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

fricas

)set output algebra on

fricas

)set output tex off

fricas

eigenvectors(u1::Matrix FRAC POLY INT)

   Cannot convert the value from type Variable(u1) to Matrix(Fraction(
      Polynomial(Integer))) .

fricas

)set output algebra off

fricas

)set output tex on

The scalar product must be non-degenerate:

fricas

Ů:=determinant u1

   There are 3 exposed and 1 unexposed library operations named 
      determinant having 1 argument(s) but none was determined to be 
      applicable. Use HyperDoc Browse, or issue
                           )display op determinant
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named 
      determinant with argument type(s) 
                                Variable(u1)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Frobenius scalar product of "vectors" and

fricas

a:=sb('a,[1])*i+sb('a,[2])*j

$\label{eq10}{{a_{2}}\ j}+{{a_{1}}\ i}$

(10)

Type: Polynomial(Integer)

fricas

b:=sb('b,[1])*i+sb('b,[2])*j

$\label{eq11}{{b_{2}}\ j}+{{b_{1}}\ i}$

(11)

Type: Polynomial(Integer)

fricas

(a,a)/Ų

   There are 11 exposed and 15 unexposed library operations named / 
      having 2 argument(s) but none was determined to be applicable. 
      Use HyperDoc Browse, or issue
                                )display op /
      to learn more about the available operations. Perhaps 
      package-calling the operation or using coercions on the arguments
      will allow you to apply the operation.

   Cannot find a definition or applicable library operation named / 
      with argument type(s) 
                         Tuple(Polynomial(Integer))
                                 Variable(Ų)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Definition 3

Co-scalar product

Solve the Snake Relation as a system of linear equations.

fricas

Ω:𝐋:=Σ(Σ(script('u,[[i,j]])*𝐞.i*𝐞.j, i,1..dim), j,1..dim)

   𝐋 is not a valid type.

fricas

matrix Ξ(Ξ(retract(Ω/(𝐝.i*𝐝.j)), i,1..dim), j,1..dim)

   There are no library operations named 𝐝 
      Use HyperDoc Browse or issue
                                 )what op 𝐝
      to learn if there is any operation containing " 𝐝 " in its name.
   Cannot find a definition or applicable library operation named 𝐝 
      with argument type(s) 
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.
   FriCAS will attempt to step through and interpret the code.
   There are no library operations named 𝐝 
      Use HyperDoc Browse or issue
                                 )what op 𝐝
      to learn if there is any operation containing " 𝐝 " in its name.

   Cannot find a definition or applicable library operation named 𝐝 
      with argument type(s) 
                               PositiveInteger

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Check "dimension" and the snake relations.

fricas

O:𝐋:=
       Ω    /
       Ų

   𝐋 is not a valid type.

Definition 4

Co-algebra

Compute the "three-point" function and use it to define co-multiplication.

fricas

W:=
  (Y I) /
    Ų

   There are no exposed library operations named Y but there are 2 
      unexposed operations with that name. Use HyperDoc Browse or issue
                                )display op Y
      to learn more about the available operations.

   Cannot find a definition or applicable library operation named Y 
      with argument type(s) 
                                 Variable(I)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

fricas

test
     (    I ΩX     )  /
     (     Y I     )  =  λ

   There are no exposed library operations named I but there is one 
      unexposed operation with that name. Use HyperDoc Browse or issue
                                )display op I
      to learn more about the available operation.

   Cannot find a definition or applicable library operation named I 
      with argument type(s) 
                                Variable(ΩX)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Co-associativity

fricas

test(
  (  λ  ) / _
  ( I λ ) = _
  (  λ  ) / _
  ( λ I ) )

   There are no exposed library operations named I but there is one 
      unexposed operation with that name. Use HyperDoc Browse or issue
                                )display op I
      to learn more about the available operation.

   Cannot find a definition or applicable library operation named I 
      with argument type(s) 
                                 Variable(λ)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

fricas

test
         e     /
         λ     =    ΩX

$\label{eq12} \mbox{\rm false}$

(12)

Type: Boolean

Frobenius Condition (fork)

fricas

H :=
         Y    /
         λ

$\label{eq13}\frac{Y}{��}$

(13)

Type: Fraction(Polynomial(Integer))

fricas

test
     (   λ I   )  /
     (  I Y    )  =  H

   There are no library operations named λ 
      Use HyperDoc Browse or issue
                                 )what op λ
      to learn if there is any operation containing " λ " in its name.

   Cannot find a definition or applicable library operation named λ 
      with argument type(s) 
                                 Variable(I)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Handle

fricas

Φ :=
         λ     /
         Y

$\label{eq14}\frac{��}{Y}$

(14)

Type: Fraction(Polynomial(Integer))

Figure 12

fricas

φφ:=          _
  ( Ω  Ω  ) / _
  ( X I I ) / _
  ( I X I ) / _
  ( I I X ) / _
  (  Y  Y )

   There are no library operations named Ω 
      Use HyperDoc Browse or issue
                                 )what op Ω
      to learn if there is any operation containing " Ω " in its name.

   Cannot find a definition or applicable library operation named Ω 
      with argument type(s) 
                                 Variable(Ω)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Bi-algebra conditions

fricas

ΦΦ:=          _
  (  λ λ  ) / _
  ( I I X ) / _
  ( I X I ) / _
  ( I I X ) / _
  (  Y Y  )

   There are no library operations named λ 
      Use HyperDoc Browse or issue
                                 )what op λ
      to learn if there is any operation containing " λ " in its name.

   Cannot find a definition or applicable library operation named λ 
      with argument type(s) 
                                 Variable(λ)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Bi-algebra conditions

fricas

ΦΦ:=          _
  (  λ λ  ) / _
  ( I X I ) / _
  (  Y Y  )

   There are no library operations named λ 
      Use HyperDoc Browse or issue
                                 )what op λ
      to learn if there is any operation containing " λ " in its name.

   Cannot find a definition or applicable library operation named λ 
      with argument type(s) 
                                 Variable(λ)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Y-forms

Three traces of two graftings of an algebra gives six (2,0)-forms.

Left snail and right snail:

  LS                    RS

  Y /\                    /\ Y
   Y  )                  (  Y
    \/                    \/

  i  j                        j  i
   \/                          \/
    \    /\              /\    /
     e  f  \            /  f  e
      \/    \          /    \/
       \    /          \    /
        f  /            \  f
         \/              \/

fricas

LS:=
  ( Y Λ  )/ _
  (  Y I )/ _
      V

   There are no exposed library operations named Y but there are 2 
      unexposed operations with that name. Use HyperDoc Browse or issue
                                )display op Y
      to learn more about the available operations.

   Cannot find a definition or applicable library operation named Y 
      with argument type(s) 
                                 Variable(Λ)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Left and right deer:

   RD                 LD

   \ /\/              \/\ /
    Y /\              /\ Y
     Y  )            (  Y
      \/              \/

   i            j    i            j
    \    /\    /      \    /\    /
     \  f  \  /        \  /  f  /
      \/    \/          \/    \/
       \    /\          /\    /
        e  /  \        /  \  e
         \/    \      /    \/
          \    /      \    /
           f  /        \  f
            \/          \/

Left and right deer forms are identical but different from snails.

fricas

RD:=
  (  I Λ I  ) / _
  (   Y X   ) / _
  (    Y I  ) / _
        V

   There are no library operations named Λ 
      Use HyperDoc Browse or issue
                                 )what op Λ
      to learn if there is any operation containing " Λ " in its name.

   Cannot find a definition or applicable library operation named Λ 
      with argument type(s) 
                                 Variable(I)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

Left and right turtles:

  RT                   LT

   /\ / /               \ \ /\
  (  Y /                 \ Y  )
   \  Y                   Y  /
    \/                     \/

           i     j      i     j
    /\    /     /        \     \    /\
   /  f  /     /          \     \  f  \
  /    \/     /            \     \/    \
  \     \    /              \    /     /
   \     e  /                \  e     /
    \     \/                  \/     /
     \    /                    \    /
      \  f                      f  /
       \/                        \/

fricas

RT:=
  (  Λ I I ) / _
  ( I Y I  ) / _
  (  I Y   ) / _
      V

   There are no exposed library operations named I but there is one 
      unexposed operation with that name. Use HyperDoc Browse or issue
                                )display op I
      to learn more about the available operation.

   Cannot find a definition or applicable library operation named I 
      with argument type(s) 
                                 Variable(I)

      Perhaps you should use "@" to indicate the required return type, 
      or "$" to specify which version of the function you need.

The turles are symmetric

fricas