help links subscribe changes refresh edit

	Frobenius Algebra, Vector Spaces and Polynomial Ideals
Octonion Algebra is Frobenius in Just One Way ←	↑	→ SandBox Quaternion Algebra is Frobenius in Many Ways

SandBox Grassmann Algebra Is Frobenius In Many Ways

Edit detail for SandBox Grassmann Algebra Is Frobenius In Many Ways revision 3 of 8

	1 2 3 4 5 6 7 8
Editor: Bill Page Time: 2011/04/05 14:25:04 GMT-7
Note: AntiSymm

added:
Generate structure constants for Grassmann Algebra
\begin{axiom}
-- Construct a basis for the Grassmann algebra
GA:=AntiSymm(INT,[subscript(g,[i]) for i in 1..n])
B:=[exp(reverse concat([0 for i in 1..n-length(x)],wholeRagits(x::RADIX(2))))$GA for x in 0..dim-1]
-- Compute the multiplication table
M:=matrix [[B.i * B.j for j in 1..dim] for i in 1..dim]
-- The structure constants of the algebra are given by the coefficients
-- of the polynomials in the multiplication table with respect to the basis
S(y)==map(x+->coefficient(x,y),M)
Yg:T:=unravel concat concat(map(S,B)::List List List FRAC POLY INT)
\end{axiom}

-dimensional vector space representing Grassmann algebra with generators

An algebra is represented by a (2,1)-tensor $Y=\{ {y^k}_{ij} \ i,j,k =1,2, ... dim \}$ viewed as a linear operator with two inputs and one output . For example:

axiom

n:=2

$\label{eq1}2$

(1)

Type: PositiveInteger?

axiom

dim:=2^n

$\label{eq2}4$

(2)

Type: PositiveInteger?

axiom

T:=CartesianTensor(1,dim,FRAC POLY INT)

$\label{eq3}\hbox{\axiomType{CartesianTensor}\ } (1, 4, \hbox{\axiomType{Fraction}\ } (\hbox{\axiomType{Polynomial}\ } (\hbox{\axiomType{Integer}\ })))$

(3)

Type: Type

axiom

Y:T := unravel(concat concat
  [[[script(y,[[i,j],[k]])
    for i in 1..dim]
      for j in 1..dim]
        for k in 1..dim]
          )

$\label{eq4}\begin{array}{@{}l} \displaystyle \left[{\left[ \begin{array}{cccc} {y_{1, \: 1}^{1}}&{y_{2, \: 1}^{1}}&{y_{3, \: 1}^{1}}&{y_{4, \: 1}^{1}} \ {y_{1, \: 2}^{1}}&{y_{2, \: 2}^{1}}&{y_{3, \: 2}^{1}}&{y_{4, \: 2}^{1}} \ {y_{1, \: 3}^{1}}&{y_{2, \: 3}^{1}}&{y_{3, \: 3}^{1}}&{y_{4, \: 3}^{1}} \ {y_{1, \: 4}^{1}}&{y_{2, \: 4}^{1}}&{y_{3, \: 4}^{1}}&{y_{4, \: 4}^{1}}$

(4)

Type: CartesianTensor?(1,4,Fraction(Polynomial(Integer)))

Generate structure constants for Grassmann Algebra

axiom

-- Construct a basis for the Grassmann algebra
GA:=AntiSymm(INT,[subscript(g,[i]) for i in 1..n])

$\label{eq5}\hbox{\axiomType{AntiSymm}\ } (\hbox{\axiomType{Integer}\ } , [ <em> 01 g 1, </em> 01 g 2 ])$

(5)

Type: Type

axiom

B:=[exp(reverse concat([0 for i in 1..n-length(x)],wholeRagits(x::RADIX(2))))$GA for x in 0..dim-1]

$\label{eq6}\left[ 1, \:{g_{1}}, \:{g_{2}}, \:{{g_{1}}\ {g_{2}}}\right]$

(6)

Type: List(AntiSymm?(Integer,[*01g1,*01g2]))

axiom

-- Compute the multiplication table
M:=matrix [[B.i * B.j for j in 1..dim] for i in 1..dim]

$\label{eq7}\left[ \begin{array}{cccc} 1 &{g_{1}}&{g_{2}}&{{g_{1}}\ {g_{2}}} \ {g_{1}}& 0 &{{g_{1}}\ {g_{2}}}& 0 \ {g_{2}}& -{{g_{1}}\ {g_{2}}}& 0 & 0 \ {{g_{1}}\ {g_{2}}}& 0 & 0 & 0$

(7)

Type: Matrix(AntiSymm?(Integer,[*01g1,*01g2]))

axiom

-- The structure constants of the algebra are given by the coefficients
-- of the polynomials in the multiplication table with respect to the basis
S(y)==map(x+->coefficient(x,y),M)

Type: Void

axiom

Yg:T:=unravel concat concat(map(S,B)::List List List FRAC POLY INT)

axiom

Compiling function S with type AntiSymm(Integer,[*01g1,*01g2]) -> 
      Matrix(Integer)

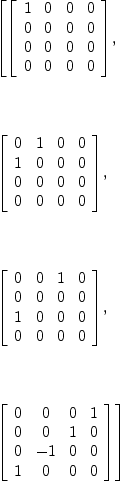$\label{eq8}\begin{array}{@{}l} \displaystyle \left[{\left[ \begin{array}{cccc} 1 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0 \ 0 & 0 & 0 & 0$

(8)

Type: CartesianTensor?(1,4,Fraction(Polynomial(Integer)))

A scalar product is denoted by the (2,0)-tensor $U = \{ u_{ij} \}$

axiom

U:T := unravel(concat
  [[script(u,[[],[j,i]])
    for i in 1..dim]
      for j in 1..dim]
        )

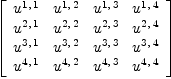$\label{eq9}\left[ \begin{array}{cccc} {u^{1, \: 1}}&{u^{1, \: 2}}&{u^{1, \: 3}}&{u^{1, \: 4}} \ {u^{2, \: 1}}&{u^{2, \: 2}}&{u^{2, \: 3}}&{u^{2, \: 4}} \ {u^{3, \: 1}}&{u^{3, \: 2}}&{u^{3, \: 3}}&{u^{3, \: 4}} \ {u^{4, \: 1}}&{u^{4, \: 2}}&{u^{4, \: 3}}&{u^{4, \: 4}}$

(9)

Type: CartesianTensor?(1,4,Fraction(Polynomial(Integer)))

Definition 1

We say that the scalar product is associative if the tensor equation holds:

    Y   =   Y
     U     U

In other words, if the (3,0)-tensor:

    i  j  k   i  j  k   i  j  k
     \ | /     \/  /     \  \/
      \|/   =   \ /   -   \ /
       0         0         0

$\label{eq10} \Phi = \{ \phi^{ijk} = {y^e}_{ij} u_{ek} - u_{ie} {y_e}^{jk} \}$

(10)

(three-point function) is zero.

axiom

YU := reindex(reindex(U,[2,1])*reindex(Y,[1,3,2]),[3,2,1])-U*Y;

Type: CartesianTensor?(1,4,Fraction(Polynomial(Integer)))

Definition 2

An algebra with a non-degenerate associative scalar product is called pre-Frobenius.

We may consider the problem where multiplication Y is given, and look for all associative scalar products or we may consider an scalar product U as given, and look for all algebras such that the scalar product is associative.

This problem can be solved using linear algebra.

axiom

)expose MCALCFN

   MultiVariableCalculusFunctions is now explicitly exposed in frame 
      initial 
K := jacobian(ravel(YU),concat(map(variables,ravel(Y)))::List Symbol);

Type: Matrix(Fraction(Polynomial(Integer)))

The matrix K transforms the coefficients of the tensor into coefficients of the tensor $\Phi$ . We are looking for coefficients of the tensor such that K transforms the tensor into $\Phi=0$ for any .

A necessary condition for the equation to have a non-trivial solution is that the matrix K be degenerate.

Consider the determinant of the matrix K above:

  \begin{axiom}
  Kd := factor(determinant(K)::DMP(concat map(variables,ravel(U)),FRAC INT))
  \end{axiom}

The scalar product must also be non-degenerate:

  \begin{axiom}
  Ud:DMP(concat map(variables,ravel(U)),FRAC INT) := determinant [[U[i,j] for j in 1..dim] for i in 1..dim]
  \end{axiom}

The basis of the null space of the K matrix:

  \begin{axiom}
  YUS:T :=  reindex(reindex(US,[2,1])*reindex(Y,[1,3,2]),[3,2,1])-US*Y
  KS := jacobian(ravel(YUS),concat(map(variables,ravel(Y)))::List Symbol);
  NS:=nullSpace(KS)
  SS:=map((x,y)+->x=y,concat map(variables,ravel Y),
    entries reduce(+,[p[i]*NS.i for i in 1..#NS]))
  YS:T := unravel(map(x+->subst(x,SS),ravel Y))
  \end{axiom}

This defines a family of pre-Frobenius algebras:

  \begin{axiom}
  test(unravel(map(x+->subst(x,SS),ravel YUS))$T=0*YU)
  \end{axiom}

Alternatively we may consider

axiom

J := jacobian(ravel(YU),concat(map(variables,ravel(U)))::List Symbol);

Type: Matrix(Fraction(Polynomial(Integer)))

The matrix J transforms the coefficients of the tensor into coefficients of the tensor $\Phi$ . We are looking for coefficients of the tensor such that J transforms the tensor into $\Phi=0$ for any .

A necessary condition for the equation to have a non-trivial solution is that all 70 of the 4x4 sub-matrices of J are degenerate. To this end we can form the polynomial ideal of the determinants of these sub-matrices:

  \begin{axiom}
  JP:=ideal concat concat concat
    [[[[ determinant(
      matrix([row(J,i1),row(J,i2),row(J,i3),row(J,i4)]))
        for i4 in (i3+1)..maxRowIndex(J) ] 
          for i3 in (i2+1)..(maxRowIndex(J)-1) ]
            for i2 in (i1+1)..(maxRowIndex(J)-2) ]
              for i1 in minRowIndex(J)..(maxRowIndex(J)-3) ];
  #generators(%)
  \end{axiom}