Subject: DeRhamComplex?
If we were to create a new domain that allows metric to be part of the definition,
what should it be called?
On 7 October 2014 12:13 Kurt Pagani wrote to fricas-devel@googlegroups.com:
I have no idea. You tell me? I can't yet overview how the final module(s) should
look like. What I have in mind is first to complete this by functions like proj
(projection on homogeneous parts, subspaces), push forward/pull back, interior
product 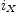 and Lie derivative
and Lie derivative 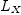 which is possible which little effort, second
to have simplicial homology (e.g. a type Simplex) then using FreeAbelianGroup?(Simplex),
defining boundaryOperator and so on such that one can deal with integration of
differential forms over simplicial complexes (Stokes theorem, Hodge pairing and
so on you know). It's almost all there but one has to organize it. It should be
a teamwork to becoming really useful, so any suggestions welcome.
which is possible which little effort, second
to have simplicial homology (e.g. a type Simplex) then using FreeAbelianGroup?(Simplex),
defining boundaryOperator and so on such that one can deal with integration of
differential forms over simplicial complexes (Stokes theorem, Hodge pairing and
so on you know). It's almost all there but one has to organize it. It should be
a teamwork to becoming really useful, so any suggestions welcome.
fricas
(1) -> )lib DERHAM
DeRhamComplex is now explicitly exposed in frame initial
DeRhamComplex will be automatically loaded when needed from
/var/aw/var/LatexWiki/DERHAM.NRLIB/DERHAM
spad
)abbrev domain DIFGEOM DifferentialGeometry
DifferentialGeometry(n:NNI, CoefRing, listIndVar : DirectProduct(n,Symbol), g:SMR) : Export == Implement where
CoefRing : Join(IntegralDomain, Comparable)
ASY ==> AntiSymm(R, listIndVar)
DERHAM ==> DeRhamComplex(CoefRing, members listIndVar)
DIFRING ==> DifferentialRing
LALG ==> LeftAlgebra
FMR ==> FreeMod(R, EAB)
I ==> Integer
L ==> List
EAB ==> ExtAlgBasis -- these are exponents of basis elements in order
NNI ==> NonNegativeInteger
O ==> OutputForm
R ==> Expression(CoefRing)
SMR ==> SquareMatrix(n,R)
Export == Join(LALG(R), RetractableTo(R)) with
leadingCoefficient : % -> R
++ leadingCoefficient(df) returns the leading
++ coefficient of differential form df.
leadingBasisTerm : % -> %
++ leadingBasisTerm(df) returns the leading
++ basis term of differential form df.
reductum : % -> %
++ reductum(df), where df is a differential form,
++ returns df minus the leading
++ term of df if df has two or more terms, and
++ 0 otherwise.
coefficient : (%, %) -> R
++ coefficient(df, u), where df is a differential form,
++ returns the coefficient of df containing the basis term u
++ if such a term exists, and 0 otherwise.
generator : NNI -> %
++ generator(n) returns the nth basis term for a differential form.
homogeneous? : % -> Boolean
++ homogeneous?(df) tests if all of the terms of
++ differential form df have the same degree.
retractable? : % -> Boolean
++ retractable?(df) tests if differential form df is a 0-form,
++ i.e., if degree(df) = 0.
degree : % -> NNI
++ changed from I to NNI , then works
++ degree(df) returns the homogeneous degree of differential form df.
map : (R -> R, %) -> %
++ map(f, df) replaces each coefficient x of differential
++ form df by \spad{f(x)}.
totalDifferential : R -> %
++ totalDifferential(x) returns the total differential
++ (gradient) form for element x.
exteriorDifferential : % -> %
++ exteriorDifferential(df) returns the exterior
++ derivative (gradient, curl, divergence, ...) of
++ the differential form df.
--=-=-=-=-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-=
dim : % -> NNI
++ dimension of underlying space
++ that is dim ExtAlg = 2^dim
hodgeStar : (%) -> %
++ computes the Hodge dual of the differential form % with respect
++ to a metric g.
dot : (%,%) -> R
++ computes the inner product of two differential forms w.r.t. g
proj : (%,NNI) -> %
++ projection to homogeneous terms of degree p
interiorProduct : (Vector(R),%) -> %
++ calculates the interior product i_X(a) of the vector field X
++ with the differential form a (w.r.t. metric g).
lieDerivative : (Vector(R),%) -> %
++ calculates the Lie derivative L_X(a) of the differential
++ form a with respect to the vector field X (w.r.t. metric g).
--=-=-=-=-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-=
Implement == DERHAM add
Rep := DERHAM
terms : % -> List Record(k : EAB, c : R)
terms(a) ==
-- it is the case that there are at least two terms in a
a pretend List Record(k : EAB, c : R)
--=-=-=-=-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-=
-- error messages
err2:="Not implemented"
err3:="Degenerate metric"
err4:="Index out of range"
-- coord space dimension
dim(f) == n
-- flip 0->1, 1->0
flip(b:ExtAlgBasis):ExtAlgBasis ==
bl := b pretend List(NNI)
[(i+1) rem 2 for i in bl] pretend ExtAlgBasis
-- list the positions of a's (a=0,1) in x
pos(x:EAB, a:NNI):List(NNI) ==
y:= x pretend List(NNI)
[j for j in 1..#y | y.j=a]
-- compute dot of singletons
dot1(r:Record(k : EAB, c : R),s:Record(k : EAB, c : R)):R ==
test(r.k ~= s.k) => 0::R
idx := pos(r.k,1)
idx = [] => r.c * s.c
reduce("*",[1/g(j,j) for j in idx]::List(R)) * r.c * s.c
-- export
dot(x,y) ==
tx := terms(x)
ty := terms(y)
reduce("+",[dot1(tx.j,ty.j) for j in 1..#tx])
-- export
hodgeStar(x) ==
not diagonal? g => error(err2)
v := sqrt(abs(determinant(g))) -- volume factor
v = 0 => error(err3)
t := terms(x)
s := [copy(r) for r in t] -- we need a copy of x!
for j in 1..#t repeat
s.j.k := flip(s.j.k)
fs:= [s.j] pretend %
ft:= [t.j] pretend %
s.j.c := s.j.c * v * dot1(t.j,t.j)/leadingCoefficient(ft*fs)
s pretend %
-- export
proj(x,p) ==
p < 0 or p > n => error(err4)
t := terms(x)
idx := [j for j in 1..#t | #pos(t.j.k,1)=p]
s := [copy(t.j) for j in idx::List(NNI)]
s pretend %
interiorProduct(v,x) ==
f := reduce("+", [generator(i)$% for i in 1..n]::List(%))
t := terms(f)
for j in 1..n repeat
t.(n-j+1).c := g(j,j)*v(j) -- reverse order!
f -- term manipulations are destructive ;)
dg:R := determinant(g)
sg:R := dg/abs(dg)
if odd?(n) then
m:R := sg
else
m:R := (-1)^degree(x) * sg
m * hodgeStar(f * hodgeStar(x))
lieDerivative(v,x) ==
a := exteriorDifferential(interiorProduct(v,x))
b := interiorProduct(v, exteriorDifferential(x))
a+b
--=-=-=-=-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-==-=-=
spad
Compiling FriCAS source code from file
/var/lib/zope2.10/instance/axiom-wiki/var/LatexWiki/7961152715829501373-25px002.spad
using old system compiler.
DIFGEOM abbreviates domain DifferentialGeometry
------------------------------------------------------------------------
initializing NRLIB DIFGEOM for DifferentialGeometry
compiling into NRLIB DIFGEOM
****** Domain: CoefRing already in scope
compiling local terms : % -> List Record(k: ExtAlgBasis,c: Expression CoefRing)
DIFGEOM;terms is replaced by a
Time: 0.04 SEC.
compiling exported dim : % -> NonNegativeInteger
Time: 0 SEC.
compiling local flip : ExtAlgBasis -> ExtAlgBasis
Time: 0 SEC.
compiling local pos : (ExtAlgBasis,NonNegativeInteger) -> List NonNegativeInteger
Time: 0.02 SEC.
compiling local dot1 : (Record(k: ExtAlgBasis,c: Expression CoefRing),Record(k: ExtAlgBasis,c: Expression CoefRing)) -> Expression CoefRing
Time: 0.23 SEC.
compiling exported dot : (%,%) -> Expression CoefRing
Time: 0 SEC.
compiling exported hodgeStar : % -> %
Time: 0.59 SEC.
compiling exported proj : (%,NonNegativeInteger) -> %
Time: 0.02 SEC.
compiling exported interiorProduct : (Vector Expression CoefRing,%) -> %
Time: 0.02 SEC.
compiling exported lieDerivative : (Vector Expression CoefRing,%) -> %
Time: 0 SEC.
(time taken in buildFunctor: 1570)
;;; *** |DifferentialGeometry| REDEFINED
;;; *** |DifferentialGeometry| REDEFINED
Time: 0 SEC.
Warnings:
[1] dot1: k has no value
[2] dot1: c has no value
[3] hodgeStar: c has no value
Cumulative Statistics for Constructor DifferentialGeometry
Time: 0.93 seconds
finalizing NRLIB DIFGEOM
Processing DifferentialGeometry for Browser database:
--->-->DifferentialGeometry(constructor): Not documented!!!!
--------(leadingCoefficient ((Expression CoefRing) %))---------
--------(leadingBasisTerm (% %))---------
--------(reductum (% %))---------
--------(coefficient ((Expression CoefRing) % %))---------
--------(generator (% (NonNegativeInteger)))---------
--------(homogeneous? ((Boolean) %))---------
--------(retractable? ((Boolean) %))---------
--------(degree ((NonNegativeInteger) %))---------
--->-->DifferentialGeometry((degree ((NonNegativeInteger) %))): Improper first word in comments: changed
"changed from \\spad{I} to NNI ,{} then works degree(\\spad{df}) returns the homogeneous degree of differential form \\spad{df}."
--------(map (% (Mapping (Expression CoefRing) (Expression CoefRing)) %))---------
--------(totalDifferential (% (Expression CoefRing)))---------
--------(exteriorDifferential (% %))---------
--------(dim ((NonNegativeInteger) %))---------
--->-->DifferentialGeometry((dim ((NonNegativeInteger) %))): Improper first word in comments: dimension
"dimension of underlying space that is dim ExtAlg = 2^dim"
--------(hodgeStar (% %))---------
--->-->DifferentialGeometry((hodgeStar (% %))): Improper first word in comments: computes
"computes the Hodge dual of the differential form \\% with respect to a metric \\spad{g}."
--------(dot ((Expression CoefRing) % %))---------
--->-->DifferentialGeometry((dot ((Expression CoefRing) % %))): Improper first word in comments: computes
"computes the inner product of two differential forms \\spad{w}.\\spad{r}.\\spad{t}. \\spad{g}"
--------(proj (% % (NonNegativeInteger)))---------
--->-->DifferentialGeometry((proj (% % (NonNegativeInteger)))): Improper first word in comments: projection
"projection to homogeneous terms of degree \\spad{p}"
--------(interiorProduct (% (Vector (Expression CoefRing)) %))---------
--->-->DifferentialGeometry((interiorProduct (% (Vector (Expression CoefRing)) %))): Improper first word in comments: calculates
"calculates the interior product i_X(a) of the vector field \\spad{X} with the differential form a (\\spad{w}.\\spad{r}.\\spad{t}. metric \\spad{g})."
--------(lieDerivative (% (Vector (Expression CoefRing)) %))---------
--->-->DifferentialGeometry((lieDerivative (% (Vector (Expression CoefRing)) %))): Improper first word in comments: calculates
"calculates the Lie derivative \\spad{L_X}(a) of the differential form a with respect to the vector field \\spad{X} (\\spad{w}.\\spad{r}.\\spad{t}. metric \\spad{g})."
--->-->DifferentialGeometry(): Missing Description
; compiling file "/var/aw/var/LatexWiki/DIFGEOM.NRLIB/DIFGEOM.lsp" (written 15 MAR 2025 05:39:20 AM):
; wrote /var/aw/var/LatexWiki/DIFGEOM.NRLIB/DIFGEOM.fasl
; compilation finished in 0:00:00.044
------------------------------------------------------------------------
DifferentialGeometry is now explicitly exposed in frame initial
DifferentialGeometry will be automatically loaded when needed from
/var/aw/var/LatexWiki/DIFGEOM.NRLIB/DIFGEOMfricas
d ==> exteriorDifferential
Type: Void
fricas
G:=diagonalMatrix([1,1,1])
Type: Matrix(Integer)
fricas
X := DIFGEOM(3,Integer,[x,y,z],G)
Type: Type
fricas
[dx,dy,dz] := [generator(i)$X for i in 1..3]
>> System error:
#<SB-SYS:FD-STREAM for "file /var/aw/var/LatexWiki/DERHAM.NRLIB/DERHAM.fasl" {1004336DF3}>
is a fasl file compiled with SBCL 1.1.1, and can't be loaded into SBCL
2.2.9.debian.
fricas
v:=vector[U(x,y,z),V(x,y,z),W(x,y,z)]
There are no exposed library operations named U but there are 4
unexposed operations with that name. Use HyperDoc Browse or issue
)display op U
to learn more about the available operations.
Cannot find a definition or applicable library operation named U
with argument type(s)
Variable(x)
Variable(y)
Variable(z)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
fricas
interiorProduct(v,sigma)
There are 1 exposed and 0 unexposed library operations named
interiorProduct having 2 argument(s) but none was determined to
be applicable. Use HyperDoc Browse, or issue
)display op interiorProduct
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named
interiorProduct with argument type(s)
Variable(v)
Variable(sigma)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
fricas
d interiorProduct(v,dx*dy*dz)
There are 1 exposed and 0 unexposed library operations named
interiorProduct having 2 argument(s) but none was determined to
be applicable. Use HyperDoc Browse, or issue
)display op interiorProduct
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named
interiorProduct with argument type(s)
Variable(v)
Polynomial(Integer)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
fricas
eta:=lieDerivative(v,theta)
There are 1 exposed and 0 unexposed library operations named
lieDerivative having 2 argument(s) but none was determined to be
applicable. Use HyperDoc Browse, or issue
)display op lieDerivative
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named
lieDerivative with argument type(s)
Variable(v)
Variable(theta)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
fricas
proj(dx+dy*dz+dx*dy*dz,2)
There are 1 exposed and 0 unexposed library operations named proj
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op proj
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named proj
with argument type(s)
Polynomial(Integer)
PositiveInteger
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
fricas
dim(sigma)
There are 2 exposed and 0 unexposed library operations named dim
having 1 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op dim
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named dim
with argument type(s)
Variable(sigma)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
fricas
dot(sigma,sigma)
There are 3 exposed and 2 unexposed library operations named dot
having 2 argument(s) but none was determined to be applicable.
Use HyperDoc Browse, or issue
)display op dot
to learn more about the available operations. Perhaps
package-calling the operation or using coercions on the arguments
will allow you to apply the operation.
Cannot find a definition or applicable library operation named dot
with argument type(s)
Variable(sigma)
Variable(sigma)
Perhaps you should use "@" to indicate the required return type,
or "$" to specify which version of the function you need.
Laplace Operator for 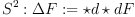
fricas
)clear all
All user variables and function definitions have been cleared.
d ==> exteriorDifferential
Type: Void
fricas
Y := DIFGEOM(2,Integer,[r,theta],diagonalMatrix([1,r^2]))
Type: Type
fricas
F:=operator 'F
fricas
[dr,dtheta] := [generator(i)$Y for i in 1..2]
>> System error:
#<SB-SYS:FD-STREAM for "file /var/aw/var/LatexWiki/DERHAM.NRLIB/DERHAM.fasl" {10045A9E83}>
is a fasl file compiled with SBCL 1.1.1, and can't be loaded into SBCL
2.2.9.debian.
fricas
)lib DIFGEOM
DifferentialGeometry is already explicitly exposed in frame initial
DifferentialGeometry will be automatically loaded when needed from
/var/aw/var/LatexWiki/DIFGEOM.NRLIB/DIFGEOM
fricas
G:=diagonalMatrix([1,1,1])
Type: Matrix(Integer)
fricas
X := DIFGEOM(3,Integer,[x',y,z],G)
Type: Type
fricas
Y := DIFGEOM(3,Integer,[x,y',z],G)
Type: Type
fricas
xy:X
Type: Void
fricas
xy:=generator(1)$X
>> System error:
#<SB-SYS:FD-STREAM for "file /var/aw/var/LatexWiki/DERHAM.NRLIB/DERHAM.fasl" {1004734413}>
is a fasl file compiled with SBCL 1.1.1, and can't be loaded into SBCL
2.2.9.debian.
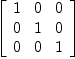
![\label{eq2}\hbox{\axiomType{DifferentialGeometry}\ } \left({3, \: \hbox{\axiomType{Integer}\ } , \:{\left[ x , \: y , \: z \right]}, \:{\left[
\begin{array}{ccc}
1 & 0 & 0
\
0 & 1 & 0
\
0 & 0 & 1
\label{eq2}\hbox{\axiomType{DifferentialGeometry}\ } \left({3, \: \hbox{\axiomType{Integer}\ } , \:{\left[ x , \: y , \: z \right]}, \:{\left[
\begin{array}{ccc}
1 & 0 & 0
\
0 & 1 & 0
\
0 & 0 & 1](images/9154359192482891798-16.0px.png)
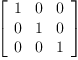
![\label{eq6}\hbox{\axiomType{DifferentialGeometry}\ } \left({3, \: \hbox{\axiomType{Integer}\ } , \:{\left[ x' , \: y , \: z \right]}, \:{\left[
\begin{array}{ccc}
1 & 0 & 0
\
0 & 1 & 0
\
0 & 0 & 1
\label{eq6}\hbox{\axiomType{DifferentialGeometry}\ } \left({3, \: \hbox{\axiomType{Integer}\ } , \:{\left[ x' , \: y , \: z \right]}, \:{\left[
\begin{array}{ccc}
1 & 0 & 0
\
0 & 1 & 0
\
0 & 0 & 1](images/3609820586149257044-16.0px.png)
![\label{eq7}\hbox{\axiomType{DifferentialGeometry}\ } \left({3, \: \hbox{\axiomType{Integer}\ } , \:{\left[ x , \: y' , \: z \right]}, \:{\left[
\begin{array}{ccc}
1 & 0 & 0
\
0 & 1 & 0
\
0 & 0 & 1
\label{eq7}\hbox{\axiomType{DifferentialGeometry}\ } \left({3, \: \hbox{\axiomType{Integer}\ } , \:{\left[ x , \: y' , \: z \right]}, \:{\left[
\begin{array}{ccc}
1 & 0 & 0
\
0 & 1 & 0
\
0 & 0 & 1](images/3526292815383393953-16.0px.png)